Лубенцова В.С. Математические модели и методы в логистике

Подождите немного. Документ загружается.

100

Заметим, что числа

образуют квадратичную матрицу

-того

порядка, на главной диагонали которой стоят нули, а элементы, рас-

положенные симметрично главной диагонали, равны по величине и

противоположны по знаку.

Отсюда следует, что задать поток

{

}

= на сети – означает

задать

, чисел удовлетворяющих условиям (6.1) – (6.3).

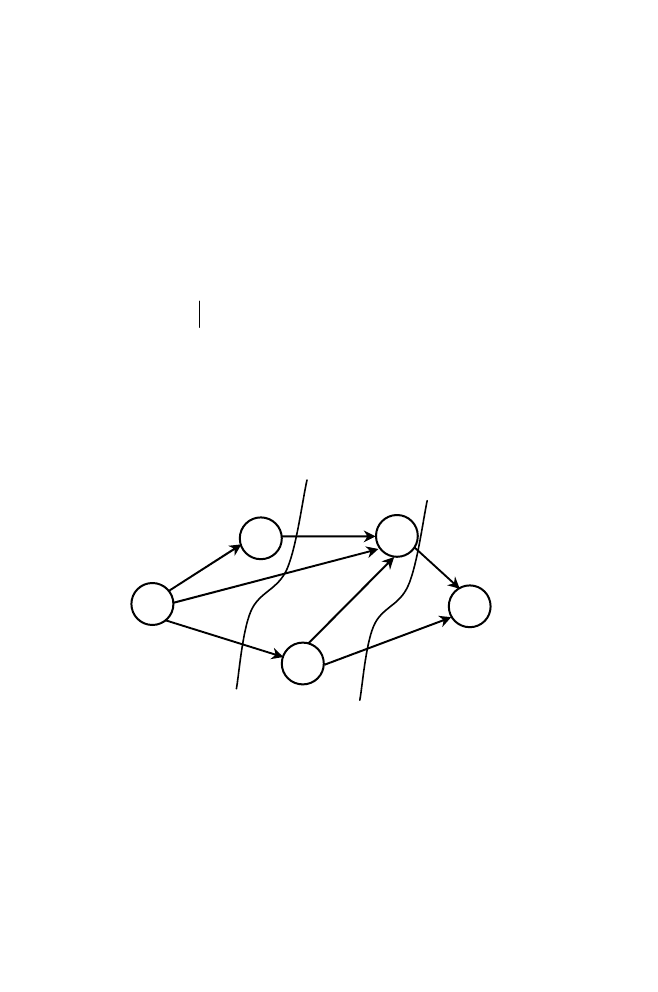
Рассмотрим, как организовать какой-нибудь поток на сети

(см. рис. 6.3).

С этой целью рассмотрим, например путь 1 - 2 - 5 – 6 (см.

рис. 6.3) – это полный путь от источника к стоку. Ребро (2,5), лежа-

щее на этом пути, не позволяет пропустить больше 1 единицы веще-

ства. Следовательно, поток по указанному пути мощностью в 1 ед.

будет допустимым:

(

)

(

)

21251225

110

xxxx

+=−+=−+=

На пути 1 - 4 - 5 - 6 можно пропустить 2 ед. вещества (лимити-

рующим является ребро 1 - 4).

На пути 1 - 3 - 6 можно пропустить 4 ед. вещества.

В результате потоки по ребрам равны:

123

=+=

, а по остальным ребрам сети потоки

равны нулю.

В соответствии с формулой (6.4) мощность сформированного

потока

1213143656

fxxxxx

=++=+=

ед.

Чтобы ответить на вопрос, будет ли этот поток максимальным,

необходимо его исследовать, а пока запишем сформированный поток

в виде матрицы (табл. 6.3).

Т а б л и ц а 6.3

i, j 1 2 3 4 5 6

1 0 1 4 2 0 0

2 -1 0 0 0 1 0

3 -4 0 0 0 0 4

4 -2 0 0 0 2 0

5 0 -1 0 -2 0 3

6 0 0 -4 0 -3 0

101

ЛЕКЦИЯ 12

6.5. Разрез на сети. Теорема Форда-Фалкерсона

Пусть дана некоторая сеть. Разобьем множество вершин сети на

два не пересекающихся подмножества А и В так, чтобы исток I попал

в подмножество А, а сток S – в подмножество В. В этом случае гово-

рят, что на сети произведен разрез, отделяющий источник I от стока

S. В результате произведенного разбиения вершин появятся ребра

(

)

, конечные точки которых окажутся в разных подмножествах.

Совокупность ребер

(

)

, начальные точки которых принадлежат

подмножеству А, а конечные – подмножеству В, называют разрезом

сети и обозначают

На схеме (рис. 6.4) в скобках указана пропускная способность в

обоих направления, число потоков по ребру. Стрелкой указано на-

правление положительного потока. На сети произведены два разреза

I и II.

При разрезе I вершины сети оказались разбитыми на подмноже-

ства А (1,2) и В (3,4,5), а ребрами, образующими разрез, стали (1,3),

(1,4) и (2,4). При разрезе II – А(1,2,3,4), В(5), а образующие ребра

(3,5) и (4,5).

Введем важные для дальнейшего изложения определения.

Величина

(

)

iAjB

RABr

⊂⊂

∑∑

, (6.5)

представляющая собой сумму пропускных способностей

, называ-

(1,4)

(3,3)

(5,5)

(2,8)

(6,7)

(4,2)

Р и с. 6.4. Разрезы на сетях

(7,9)

102

ется пропускной способностью разреза.

Пусть на сети задан поток

{

}

= и произведен разрез

(

)

Величина

(

)

iAjB

XABx

⊂⊂

∑∑

, (6.6)

представляющая собой сумму потоков

по всем ребрам разреза,

называется потоком через разрез.

Для разреза I:

(

)

131424

6219,

RIrrr

=++=++=

(

)

131424

4217.

XIxxx

=++=++=

Для разреза II:

(

)

4535

459,

RIIrr

=+=+=

(

)

4535

347.

XIIxx

=+=+=

Если на сети задан поток

{

}

= и произведен разрез

, то

хотя бы одно ребро любого полного пути, ведущего из источника I в

сток S, будет обязательно принадлежать разрезу

При этом величина потока по любому пути не превышает про-

пускную способность каждого его ребра, поэтому величина X сум-

марного потока, устремленного из источника I в сток S, не может

превысить пропускную способность любого разреза сети, то есть

ijij

iAjBiAjB

⊂⊂⊂⊂

≤

∑∑∑∑

. (6.7)

Оказывается, если удаётся построить на сети поток

{

}

= ,

величина которого равна пропускной способности некоторого разре-

за

, то этот поток будет максимальным, а разрез

обладает

минимальной пропускной способностью.

В самом деле, пусть для потока

{

}

= и разреза

выпол-

няется равенство

ijij

iAjBiAjB

⊂⊂⊂⊂

∑∑∑∑

, (6.8)

но максимальным является не

, а поток

{

}

= ; в таком случае

поток через разрез

потока

будет больше потока через этот

103

же разрез

, то есть

ijij

iAjBiAjB

⊂⊂⊂⊂

≤

∑∑∑∑

(6.9)

или

ijij

iAjBiAjB

⊂⊂⊂⊂

≤

∑∑∑∑

, (6.10)

что противоречит неравенству (6.5).

Приведенные рассуждения приводят к следующей теореме.

Теорема Форда-Фалкерсона.

На любой сети максимальная величина потока из источника I в

сток S равна минимальной пропускной способности разреза, отде-

ляющего I от S.

Эта теорема имеет важное прикладное значение.

6.6. Алгоритм решения задачи о максимальном потоке

Пусть на сети задан некоторый поток

{

}

= . Разобьем все

вершины сети на два подмножества А и В следующим образом: к

подмножеству А отнесем исток I и все вершины i, достижимые из I

хотя бы по одному пути, состоящему из ненасыщенных ребер; к

подмножеству В отнесем все остальные вершины, то есть такие, ко-

торые нельзя достичь по ненасыщенным ребрам.

При этом возможны следующие случай:

1) сток

∉

;

2) сток

∈

Рассмотрим оба этих случая.

Случай 1. Если

∉

, то

∈

, поэтому построенное разбиение

является разрезом

. По условию разбиения для любой вершины

∈

существует путь из I в i, состоящий из ненасыщенных ребер, а

для любой вершины

∈

такого пути нет. Отсюда следует, что лю-

бое ребро

(

)

разреза

(

∈

) будет насыщенным (иначе

j принадлежало бы А), то есть

. Просуммировав эти равенства

по всем

∈

, получим

ijij

iAjBiAjB

⊂⊂⊂⊂

∑∑∑∑

. (6.11)

В равенстве (6.11) слева X – величина потока через разрез, спра-

104

ва – пропускная способность разреза

. По теореме Форда-

Фалкерсона следует, что поток

{

}

= является максимальным.

Случай 2. Если

∈

, то существует путь из ненасыщенных ре-

бер, ведущий из I в S. По ребрам этого пути можно пропустить до-

полнительный поток величиной

{

}

min

ijij

∆=−. Потоки

по всем

остальным ребрам сети остаются прежними. В результате мощность

суммарного потока возрастает на величину

∆

. Это будет новый по-

ток

{

}

= .

Объединяя оба рассмотренных случая, можно предположить

следующий алгоритм построения максимального потока.

1. Построить некоторый начальный поток

{

}

= .

2. Организовать процедуру составления подмножества А вер-

шин, достижимых из источника I по насыщенным ребрам. Если в

этом процессе сток S не попадает в подмножество А, то построенный

поток максимальный и задача решена. Если же S попал в А, по пе-

рейти к пункту 3 алгоритма.

3. Выделить путь из I в S, состоящий из ненасыщенных ребер и

увеличить поток

по каждому ребру этого пути на величину

{

}

min

ijij

∆=−, где минимум берется по ребрам

(

)

упомянутого

пути. Тем самым будет построен новый поток

{

}

= . После этого

надо возвратиться к пункту 2 алгоритма.

При выполнении пункта 3 на каждом шаге по крайней мере одно

из ненасыщенных ребер становится насыщенным (именно то, кото-

рое соответствует

∆

), а поскольку число ребер в сети конечно, через

конечное число шагов максимальный поток будет построен.

Пример. Рассмотрим сеть,

представленную на рис. 6.5.

Матрица R пропускных способ-

ностей данной сети задана табл. 6.4.

В соответствии с пунктом 1 ал-

горитма на сети необходимо сфор-

мировать какой-либо начальный по-

ток. Примем в качестве такого пото-

ка

, в котором по пути 1–3–5–6

(4,6)

(2,2)

(7,3)

(1,5)

(2,5)

(4,6)

(5,7)

(8,3)

(4,9)

Р и с. 6.5

105

перемещают 2 единицы (по ребру (3,5) больше пропустить нельзя).

Т а б л и ц а 6.4

i, j 1 2 3 4 5 6

1 0 7 4 2 0 0

2 3 0 8 4 1 0

3 6 8 0 0 2 0

4 5 9 0 0 8 4

5 0 5 2 3 0 5

6 0 0 0 6 7 0

По пути 1–2–5–6 имеем 1 единицу: здесь лимитирующим явля-

ется ребро (2,5); по пути 1–4–6 имеем 2 единицы. При этом ребро

(1,4) становится насыщенным. Матрица потока

приведена

в табл. 6.5:

Т а б л и ц а 6.5

i, j 1 2 3 4 5 6

1 0 1 2 2 0 0

2 -1 0 0 0 1 0

3 -2 0 0 0 2 0

4 -2 0 0 0 0 2

5 0 -1 -2 0 0 3

6 0 0 0 -2 -2 0

Определим мощность потока:

121314

fxxx

=++=

4656

235.

fxx

=+=+=

Приступим к пункту 2 алгоритма. Составим матрицу (

−

элементы которой

(

)

− позволяют судить о насыщенности ребер

сети. Насыщенным ребрам будут соответствовать нулевые элементы,

а ненасыщенным – ненулевые (табл. 6.6).

Зная матрицу

−

, можно сформулировать подмножество А

вершин, в которые можно попасть из истока I, двигаясь по ненасы-

щенным путям (пункт 2 алгоритма), а также выделить (если поток

не оптимален) эти пути и с их помощью увеличить мощность

106

потока.

Т а б л и ц а 6.6

i, j 1 2 3 4 5 6

1 0 6 2 0 0 0

2 4 0 8 4 0 0

3 8 8 0 0 0 0

4 7 9 0 0 8 2

5 0 6 4 3 0 2

6 0 0 0 8 10 0

Вершины подмножества А выделяют из всего подмножества

вершин постепенно, начиная с I. С этой целью просматривают пер-

вую строку матрицы

−

и выписывают номера

,,...,

iii

вершин,

соответствующих ненулевым элементам строки. Это и будут верши-

ны, в которые можно попасть из источника I, перемещаясь по нена-

сыщенным ребрам. Будем записывать полученные таким образом

вершины в виде I ||

,,...,

iii

и называть подобную запись списком

вершины I. Далее рассматривают каждую из вершин

полученного

списка и составляют для нее аналогичным образом свой список. При

этом вершины, встречающиеся в прежних списках, повторно не вы-

писываются.

Если в этом процессе сток S не встретится, то поток максимален

и задача решена, если же при составлении очередного списка в нем

появится сток S, поток не максимален и мощность его можно увели-

чить.

В рассмотренном примере I = 1, S = 6. В первой строке матрицы

−

в список вершины 1 войдут вершины 2, 3– 1 || 2, 3; для вер-

шины 2 – 2 || 4; для вершины 3 – 3 || •; для вершины 4 – 4 || 5, 6.

Получили набор списков. Сток S = 6 попал в список одной из

вершин. Значит , поток

не максимален и существует путь из ис-

точника I в сток S (из 1 в 6), состоящий из ненасыщенных ребер.

Построение ненасыщенного потока большей мощности начина-

ем с последнего ребра этого пути

(

)

−

, где

−

– вершина, в спи-

сок которой попал сток S. Ребром

(

)

−−

является ребро (2,4),

ребром

(

)

– ребро (1,2). Таким образом, путь из истока в сток по

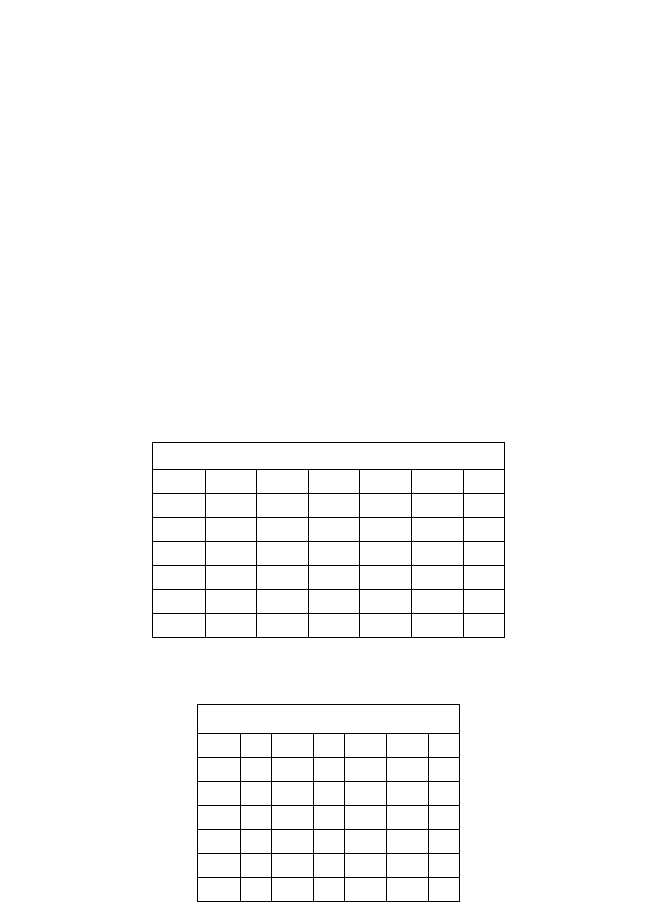
107

ненасыщенным ребрам пройдет через вершины 1, 2, 4, 6.

После выделения ненасыщенного пути из истока I в сток S оста-

ется c помощью матрицы

−

определить величину

{

}

min

ijij

∆=−, на которую нужно увеличить поток по каждому

ребру

(

)

выделенного пути, чтобы получить новый поток

мощности, большей на

∆

единиц.

В нашем примере по ребру (1,2) можно дополнительно пропус-

тить 6 единиц; по ребру (2,4) – 4 единицы; по ребру (4,6) – 2 едини-

цы. Значит, поток по всему пути 1–2–4–6, составленному из указан-

ных ребер, можно увеличить на величину

{

}

min6,4,22

∆==

(едини-

цы).

Для построения матрицы нового потока

к соответствующим

элементам матрицы

прибавляют найденное значение

∆=

возвращаются к пункту 2 алгоритма (табл. 6.7, 6.8).

Т а б л и ц а 6.7

i, j 1 2 3 4 5 6

1 0 3 2 2 0 0

2 –3 0 0 2 1 0

3 –2 0 0 0 2 0

4 –2 –2 0 0 0 4

5 0 –1 –2 0 0 3

6 0 0 0 –4 –3 0

Т а б л и ц а 6.8

−

i, j 1 2 3 4 5 6

1 0 4 2 0 0 0

2 6 0 8 2 0 0

3 8 8 0 0 0 0

4 7 11 0 0 8 0

5 0 6 4 3 0 2

6 0 0 0 10 10 0

При этом величина

108

2327

=++=

Приведем списки вершин по ненасыщенным путям:

1 || 2, 3,

2 || 4,

3 || • ,

4 || 5,

5 || 6.

Сток S оказался в подмножестве А, а путь, ведущий к нему, содер-

жит ребра

(

)

1,2,

(

)

2,4,

(

)

4,5,

(

)

5,6

; тогда

(

)

min4,2,8,2

∆= .

Новый поток

получается путем увеличения соответствую-

щим элементом потока

. Соотвествующие вычисления приведены

в табл. 6.9 и 6.10.

Т а б л и ц а 6.9

i, j 1 2 3 4 5 6

1 0 5 2 2 0 0

2 -5 0 0 4 1 0

3 -2 0 0 0 2 0

4 -2 -4 0 0 2 4

5 0 -1 -2 -2 0 5

6 0 0 0 -4 -5 0

Списки вершин по ненасыщенным путям:

1||2, 3,

2||3,

3 || • .

Т а б л и ц а 6. 10

−

i, j 1 2 3 4 5 6

1 0 2 2 0 0 0

2 8 0 8 0 0 0

3 8 8 0 0 0 0

4 7 13 0 0 6 0

5 0 6 4 5 0 0

6 0 0 0 10 12 0

Здесь имеем

109

Далее, списки вершин по ненасыщенным путям:

1 || 2, 3,

2 ||•,

3 || • .

Сток 6 не попал в подмножество А вершин, достижимых из ис-

точника 1 по ненасыщенным путям. Значит, поток

максимален.

Остается нанести его на сеть с указанием направления потоков по

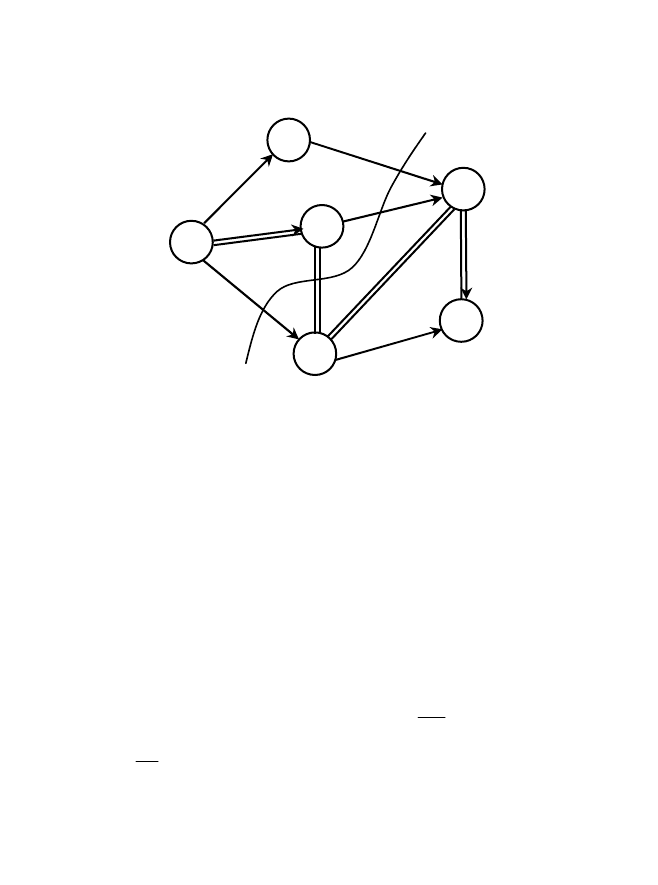
отдельным ребрам (рис. 6.6).

Используя список, выделим подмножества А и В, на которые

оказалось разбитым множество всех вершин: А={1, 2, 3}, В={4, 5, 6}.

Отсюда можно выписать ребра, образующие разрез А | В минималь-

ной пропускной способности: (1, 4); (2, 4); (2, 5); (3, 5). В итоге полу-

чим:

21429

=+++=

6.7. Приложение алгоритма о максимальном потоке

к решению транспортной задачи по критерию времени

Приложением задачи о максимальном потоке является транс-

портная задача по критерию времени.

Пусть известны запасы груза

(

)

= у поставщиков

спрос

(

)

= потребителей

– время поставки груза (не-

зависимо от объема поставки) по маршруту

—

. Требуется со-

ставить план перевозок, при котором спрос, реализуемый за мини-

мальное время, удовлетворяется полностью.

Р и с. 6.6