Лобанов А.Н. Фотограмметрия

Подождите немного. Документ загружается.

где X, У, 1 — координаты точки местности; х, у — координаты

точки снимка; Х

, У

, 2

— координаты точки фотографирования;

/ — фокусное расстояние снимка; х

, у

— координаты главной

точки снимка; щ, Ь(, сс — направляющие косинусы, зависящие от

угловых элементов внешнего ориентирования снимка а, со и к

и вычисляемые по формулам (9.8); Х*У* — числители дроби; 2* —

знаменатель дроби.

В общем случае уравнения (9.12) содержат девять неизвестных:

шесть элементов внешнего ориентирования снимка и три коорди-

наты определяемой точки местности. При этом предполагается, что

элементы внутреннего ориентирования снимка известны, а коорди-

наты точки снимка измерены с возможно высокой точностью. Если

точка местности служит опорной и ее положение определено прак-

тически безошибочно, то уравнения (9.12) включают только шесть

неизвестных — элементы внешнего ориентирования снимка.

Пусть даны приближенные значения неизвестных. Тогда по

формулам (9.12) можно вычислить координаты х и у точки снимка.

Обозначим вычисленные значения этих величин через х

и у

. Оче-

видно, что они будут отличаться от измеренных х и у. Обозначим

поправки к приближенным значениям неизвестных через 8Х

, 6а, 6<м, 8х, 8Х, 6У, Ы.

Полагая, что мы имеем избыточные измерения, составим урав-

нения поправок

а6Х

+ Ь8У

с82„

+ й8а + ебсо + /бх +

-Ь 8бХ +

1г6У

+ 182 + х

— х = к;

а'8Х

+ 6'бК

+с'б2

+ а'ба + е'бсо+/'бх+

+ §'8Х + Н'8У + Г 82

(21.32)

где

дх

Л =

дХ

дх

~~дг7

дх

Ш+ а

(х— *„)];

[Ь!/ + Ь

(х: — х

)];

№ + с

(х — л-,,)];

да

•[«?! (Х-Х

)-а

(2-2,)]

дх

дсо

[с

(Х- Х

)-а

(2-2

)];

—

51П X

+ (X

У — У

2* соз

)

г дх

/=—=«/•

ох

-у о;

дх 1

— = - — Ы + а

(х — *„)];

дХ 2*

(21.33)

420.

/» = —= -—М +Ых-*,)];

5 К 2*

5х 1

I = — № +

(х

—

)];

32 2*

а' = = —[а

/ + а

(у —

«/

)]'>

5Х

5К

с = ^ +

(г/

—

г/о)];

а' = =—— [с

—

)

—

(2 —2

)] +

5а 2*

[с

(X - Х

) - а, (2 - 2

)];

5(0 V 2* соз

со

Г = =

— (* —

*о);

ох

8' = ~~~ = - -7- ^ +

(У

Уо)];

дХ 2*

Л' = -^т- = —[Ы + Ь

(у-

«/„)];

дУ 2*

V = -Щ- = _ [С

/ +

(I/

—

1/о)]-

52 2*

Частные производные а, Ь, . . . , / и а', Ь', . . . , /' были вычи-

слены в гл. 20 при определении элементов внешнего ориентирова-

ния снимка по опорным точкам. Аналогично получаются частные

производные к, I и к', I'.

Технология маршрутной фототриангуляции в данном случае

состоит в следующем. При помощи стереокомпаратора измеряют

на снимках координаты всех точек, выбранных для построения

сети. Находят приближенные значения неизвестных — элементов

внешнего ориентирования снимков и координат определяемых то-

чек, используя для этого материалы аэрофотосъемки, старую карту

и другие данные. Результаты измерения снимков, координаты

опорных точек, приближенные значения неизвестных и другие ис-

ходные данные вводят в электронную вычислительную машину.

Вычисления начинаются с введения в измеренные координаты то-

чек снимков поправок за влияние различных систематических

ошибок. Затем для каждой точки снимка, участвующей в построе-

нии сети, составляются два уравнения поправок (21.32) с весами

/> и р'. Для этого используются исправленные координаты точки

снимка. Общее число уравнений поправок всегда больше числа

421.

неизвестных. Неизвестные определяются под условием

[ру

+ Р'Р'

] = гшп путем последовательных приближений.

От уравнений поправок переходят к нормальным уравнениям,

в результате решения которых получают поправки к приближен-

ным значениям неизвестных. Введя эти поправки, находят первое

приближение неизвестных.

Чтобы вычислить второе приближение неизвестных, вновь со-

ставляют уравнения поправок. При этом используют первое при-

ближение неизвестных. Затем составляют и решают нормальные

уравнения, в результате чего получают поправки к первому при-

ближению неизвестных. После ввода этих поправок образуется

второе приближение неизвестных.

Аналогично вычисляется третье приближение неизвестных.

Этот процесс продолжается до тех пор, пока разность значений

каждого неизвестного, полученных в двух последних приближе-

ниях, будет меньше установленного допуска.

Итак, третий способ аналитической маршрутной фототриангу-

ляции позволяет построить фотограмметрическую сеть непосредст-

венно в геоцентрической системе координат или в системе коорди-

нат Гаусса, без определения элементов взаимного ориентирования

снимков. Конечно, не исключается и случай построения свободной

маршрутной сети с последующим внешним ориентированием ее по

опорным точкам. Но и в этом случае нет необходимости находить

элементы взаимного ориентирования снимков.

Для оценки точности построения фотограмметрической сети

определяют весовые коэффициенты уравненных величин. Методы

вычисления этих коэффициентов изложены в геодезической лите-

ратуре.

Третий способ обеспечивает возможность наиболее эффектив-

ного использования зафиксированных в полете элементов внешнего

ориентирования снимков и других дополнительных данных. В этом

случае фотограмметрические, геодезические и бортовые измерения

уравнивают совместно, учитывая их веса.

Составим уравнения поправок для фотограмметрических изме-

рений.

Напишем уравнения (21.32) для определяемой точки I, изобра-

зившейся на снимке /:

ац&х

+ ЬцЫ

+ с

{)

ьг

+ Лфа.1 + еубшI + /убхг + ёцЪХ]

-г

>4]б У/

+ [,уб2/ + 1ц = ну;

а:

бХ

.+ 6..6К

. +

б2

- й

Ьа

:.бсо

+ /цбх, + е'

рх

(21.34)

422.

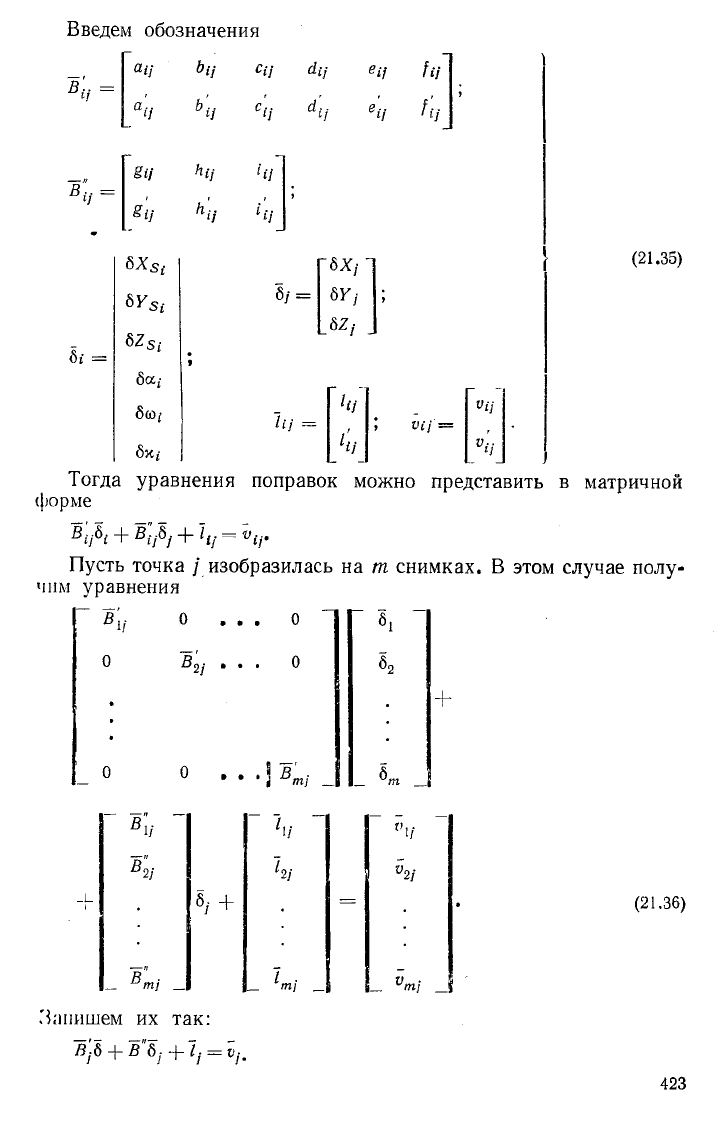
Введем обозначения

ц =

ау

Ьц

йц

и !а

йц

8Ц

лц

'<•/

'ч

8г =

и; -

6Х,-

8 У,

82,

6Х

Г8Х.1 (21-35)

ЬУз

{

Мае

бсХ;

бсо,-

Тогда уравнения поправок можно представить в матричной

форме

++ =

Пусть точка / изобразилась на т снимках. В этом случае полу-

чим уравнения

VII

; VI/=

' I т/

<'п

/ +

'2/

Ч /

т\ _

_ "щ/

Запишем их так:

;

'б + в"8

+ 7

;

= ё,-.

(21.36)

423.

Пусть в маршрутной сети к определяемых точек. Тогда можно

составить систему уравнений

В,

в"

о о

Вь

б,

(21.37)

Представим эти уравнения в^виде

(12.38)

Это выражение содержит все уравнения поправок для фото-

грамметрических измерений.

Перейдем к составлению уравнений поправок для геодезиче-

ских измерений.

Пусть X/, У/, 2/ — истинные координаты опорной точки /.

Обозначим через XУ}, 2} измеренные координаты этой точки^

а через Х°, У°, 2° — приближенные значения координат. Тогда

у.

у'.

+Х)у

=у

+ д

у .

= + =2°:+ 62,

1 1

1 1 /'

где у

, , у

— поправки к измеренным координатам, а 6Х/,

} ] /

б У/, 62/ — поправки к приближенным координатам.

Таким образом, получаем уравнения поправок

б у.

+ Г

0-у'.

б 2

}

+ Щ-2) = ь

гг

или в матричной форме

424.

(21.39)

(21.40)

1Д0

- их, -

«/ =

б2/

; 1,=

у^у.

;

Напишем уравнения поправок для I опорных точек

- б

" к ~ 1'Х

к Уг

. б, _

- 1г -

_ Щ _

(21.41)

(21.42)

и представим эти уравнения в виде

б +

= V.

?о

(21.43)

Пусть Зек — измеренное, а 8{

— приближенное расстояние

между точками I и к на местности. Тогда

где ь

и 65,-к — поправки.

Известно

1к

Х„

•х

{

)* + (У

()тсюда

65;

= абХ/ + ЬЬУ1 + сЬ2

+ а'8Х

+ Ь'ЬУ

+ с'82

Iдо а', с' — частные производные от За по соответствую-

щим переменным. Следовательно,

«6Х

;

+ ЬЬУ

+ СЬ2

+ а'8Х

+ Ь ЬУ

+ С Б2

- = О

Запишем это уравнение в матричной форме

йо б+/

"Чк гк

где В

3ш

— матрица коэффициентов, а

А*.

(21.44)

(21.45)

Пусть измерено ^ расстояний. Тогда получим уравнения по-

правок

(21.46)

425

6 1

= 1>

Аналогично можно получить уравнения поправок для других

геодезических измерений, например, для превышений, горизон-

тальных и вертикальных углов или для дирекционных углов.

Собрав уравнения поправок для всех геодезических измерений,

напишем

В"Ъ"+1" = ;". (21.47)

Теперь составим уравнения поправок для бортовых измерений.

Для координат точки фотографирования, углов наклона и угла

поворота снимка I можно написать

\ + \ =

? Ч-; + % = + <4; *( + \ = '4 + Ч,

где Х

, У'

, . . . , и' — измеренные, а , . . . , х9 — при-

ближенные элементы внешнего ориентирования снимка г,

У[

, . . . , бх*— поправки к ним.

Представим эти уравнения в матричном виде

^ +

VI,

(21.48)

где

б,=

«25,.

ба,-

;

бсо,-

бх

— —

3,- —

4 -2

У ;

_ _

(21.49)

Если элементы внешнего ориентирования измерены для т сним-

ков, то получим

"«1

_ ч, _

_ ч _ Ч _

(21.50)

426.

или в более общей форме

+ /

=--о

. (21.51)

Уравнение поправки для измеренного базиса фотографирова-

ния В'

иг

аналогично полученному выше уравнению поправки для

измеренного расстояния на местности

йЬХ

. -

ЬбК

. + сб2

. +а'бХ

+Ь',&У

4-с'Ы

III & &

Запишем его в виде

В*& +

В(к

= »в

1к

. (2!-53)

Пусть измерено § базисов фотографирования. Тогда можно со-

ставить уравнения

вЪ + 1

=д

. (21.54)

Аналогично получим уравнения поправок для других бортовых

измерений — для разностей высот фотографирования, для расстоя-

ний от центра проекции до точки отраженного импульса и т. д.

Запишем все уравнения поправок для бортовых измерений в

обобщенном виде

В"'б" + Г = (21.55)

Итак, третий способ маршрутной фототриангуляции заклю-

чается в составлении и решении трех групп уравнений поправок

для фотограмметрических, геодезических и бортовых измерений

В'Ъ' + Т =

; в"б" Г = у"; В"Т + Г" = 7.} (21.56)

Представим эти уравнения в более общем виде

1б+7 = й. (21.57)

Решая эту систему по способу наименьших квадратов, перехо-

дим к нормальным уравнениям

Ъ'ТвЬ + в'р'1 = О, (21.58)

где

Р' О О

О Р" О

О О Р"

весовая матрица измеренных величин.

Кроме рассмотренных выше существуют и другие способы по-

строения маршрутных сетей, например путем создания независи-

мых двойных моделей или путем использования прямых и обрат-

пых засечек. Однако на практике они применяются редко.

427.

§ 151. Аналитическая многомаршрутная фототриангуляция

В многомаршрутной, или блочной, фототриангуляции широко

используются фотограмметрические связи, существующие в каж-

дом маршруте и между маршрутами. Благодаря этому нет необхо-

димости обеспечивать опорными точками каждый маршрут. Для

внешнего ориентирования многомаршрутной фототриангуляции до-

статочно иметь не менее трех опорных точек на все маршруты,

составляющие блок.

Различают три способа многомаршрутной фототриангуляции:

способ связок, способ независимых моделей и способ независимых

маршрутов. Первый способ

позволяет строить и уравни-

вать сеть одновременно по

всем снимкам, входящим

в блок. Второй способ осно-

ван на построении и соеди-

нении независимых моделей.

В третьем способе сначала

создаются свободные марш-

рутные сети, а затем объеди-

няются в блок, который ори-

ентируется внешне по опор-

ным точкам.

Способ связок возник в ре-

зультате развития изложен-

ного в предыдущем параграфе

третьего способа аналити-

ческой маршрутной фото-

триангуляции. На снимках измеряют координаты выбранных

точек и определяют приближенные значения неизвестных — эле-

ментов внешнего ориентирования снимков и координат определяе-

мых точек местности. Затем для каждого изображения точки сети

составляют уравнения поправок (21.32). Таким образом получают

систему уравнений для всего блока, которую решают методом по-

следовательных приближений.

Пусть блочная сеть строится по г маршрутам, каждый из ко-

торых содержит п снимков (рис. 273). Подсчитаем общее число не-

известных и уравнений поправок в сети, полагая, что продольное

перекрытие снимков 60 %, а поперечное меньше 50 %. При этом

условимся определять шесть стандартно расположенных точек

для каждой стереопары. Определяемые точки отмечены на рис. 273

квадратами и кружками, а опорные — треугольниками.

В этом случае число снимков в блоке равно гп, а число опреде-

ляемых точек

К = п(2г+\) (21.59)

Положение каждого снимка определяется шестью элементами

внешнего ориентирования, а положение каждой определяемой

428.

О 2 о з о 3 о з О 2

Д 2 Д2

• • • • •

2 3 3 3 2

о О в о Б О В

• • • • •

2 3 3 3 2

од од

д о4

о • • • •

2 3 3 3 2

Д2 Д 2

о 2 °3 о з о з о2

Рис. 273

точки — тремя координатами. Следовательно, общее число неиз-

вестных

N = бпг +

Зга

(2г + 1)

МЛН

N = Зга (4/'

-{-

1). (21.60)

Это число определяет порядок системы нормальных уравнений.

Каждая точка снимка, представляющая собой изображение

точки сети, дает два уравнения (21.32). Таким образом, общее

число уравнений поправок в два раза больше числа изображений

точек сети на снимках. Точки сети, представленной на рис. 273,

изображаются на снимках от двух до шести раз. На этом рисунке

отмечено число изображений каждой точки сети. Число определяе-

мых точек, изобразившихся два раза, равно 2г + 4, три раза —

(//—2) (г + 2), четыре раза — 2 (г—1), шесть раз — (п—2) (г—1).

Следовательно, общее число изображений определяемых точек сети

т -= 2;(2г + 4) +

3 (га — 2)

(г + 2) + 4;(г

—

1)]2 +

6 (га — 2)

(г — 1)

ПЛИ

т = 3 (Зга — 2);л (21.61)

Пусть к— число изображений опорных точек. Тогда общее

число уравнений поправок в сети

М =6 (Зга— 2)г + 2к. (21.62)

В качестве примера рассмотрим блок, содержащий три маршрута

по 5 снимков (см. рис. 273). Согласно формулам (21.59), (21.60)

и (21.62) в этом случае сеть будет иметь:

определяемых точек К 35

неизвестных N .... 195

уравнений поправок М 234 + 2к= 254 (к — 10).

Итак, в данном случае можно составить 59 избыточных уравне-

ний поправок.

По тем же формулам получим, что при построении блочной

сети по десяти маршрутам,, в каждом из которых 10 снимков,

определяемых точек К 210

неизвестных N .... 1230

уравнений поправок М 1680 + 2к = 1700

(Л-

= 10).

Теперь с целью уменьшения времени, необходимого на построе-

ние блочной сети, сократим число определяемых точек с шести до

четырех на стереопару. Не будем включать в сеть все центральные

точки, отмеченные на рис. 273 квадратами. Тогда число определяе-

мых точек сети

/( -- я (/• + 1), (21.63)

неизвестных

/V = Зга

(Ъг

1) (21.64)

и уравнений поправок

/VI

—

4 (3пг —

2г)

+ 2к. (21.65)

429