Лобанов А.Н. Фотограмметрия

Подождите немного. Документ загружается.

Для теоретического обоснования способа используем формулы

(9.12), выражающие зависимость между координатами х и у точки

снимка и координатами X, У и 1 соответственной точки местности.

Пусть известны приближенные значения элементов ориентиро-

вания снимка. Вычислим по формулам (9.12) координаты х и у изо-

бражений опорных точек на снимке и обозначим их через (х) и'

(у).

Очевидно, вычисленные координаты будут отличаться от измерен-

ных х и у. Обозначим поправки к приближенным значениям элемен-

тов ориентирования через 6Х

, 6У

, 62

, 6а, бсо, бх, 6Д 6л;

и 8у

Полагая, что имеем избыточные измерения, составим уравне-

ния поправок

'<> ++ +1Й-

вг

* ++

дХ

К I

дХ

Я I

дХ

XI 1

дХ

+ —-бсо +— бх + —б/

б.ДГо

+ —бу

—* =

дсо дх д! дх

ду

•

У * I

У с ;

У I

У « I

У я

—

— 6ш+ —— бх + —— 6} + — 0*0 + —-оуо— У = «.

да дх д{ дх

ду

Найдем частную производную от х по Х

, обозначив числители

и знаменатель в равенствах (9.12) через X*, У*, 2* соответственно,

дх — а^' + а'Х*- 1 . ,, .

— =— / =—[а^ + а

(* —* о)].

дХ

г* 2*

Вычислим другую производную

дх _ ^Х*2* —2*Х*

да ' 2*

согласно (9.12) и (9.8):

X*' = (X — Хз) ( — 51П а

соз X —

соз а зт

со

зт

х) -{-

(У — К 5)

+ (2

—

2з)

(соз

соз

— $1П

а зт

со

зт

х)

—

Х$) + а

—

);

2* = (X

—

Х3) (— соз а соз

со)

+ (У

—

)

+ (2

—

) X

X (— зт а

соз со)

= с

—

Х5) + а

—

Следовательно,

, /

* —*о

' 2*

390

[

С1

(X - Х

) -

Я!

(2 - 2

) +

[Сз (X - Хз) — а, (2 -

2<,') 1

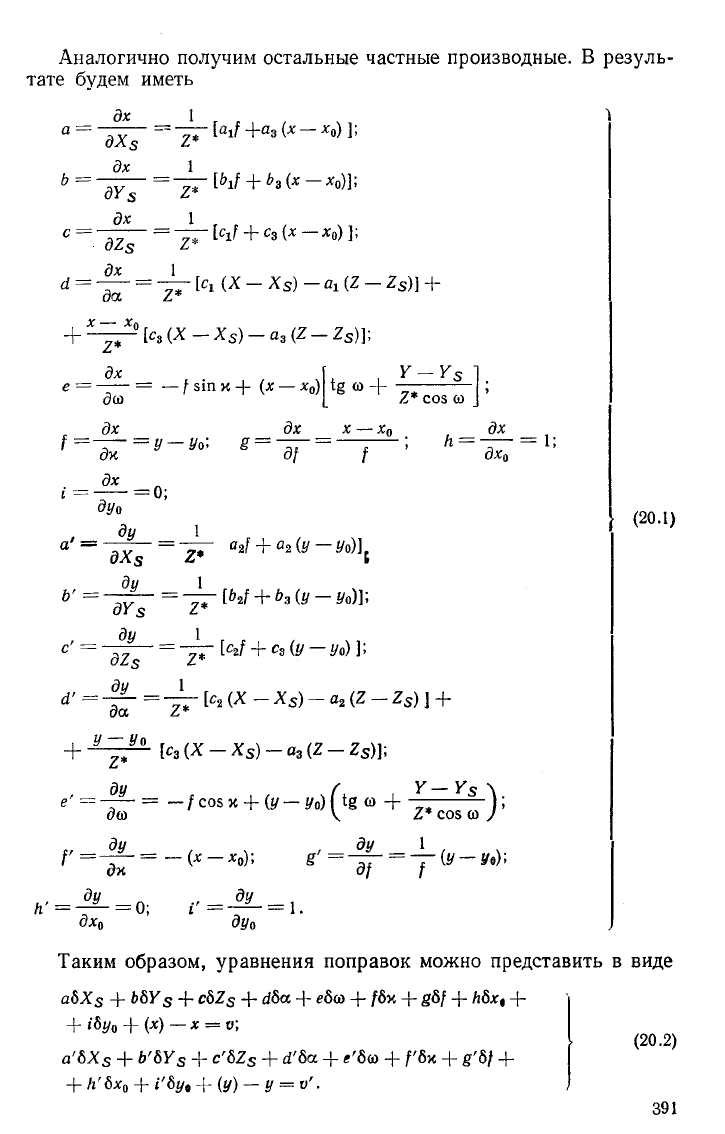
Аналогично получим остальные частные производные. В резуль-

тате будем иметь

дх

дХ

дх 1

+ Ь

(х — х

)];

дх

дг

дх

да 2

х — х

[с

(Х-Х

)-а

(2-2

)] +

[с

(Х-Х

)-а

(2-2

)];

дх

е =

——

— }

зт х + (х — х

)

дсо

Т.*

соз

со

дх

ду о

—

Уо,

= 0;

дх

—

д!

дх

= — = 1;

дх

ду

дУ

ду

[Ы + ^з (у — г/о)];

Ш + с

(у — уо)У.

д2

ди 1

-г—=—МХ-Х

)-аг(2-2

)] +

да 2*

у — г/о

ду

[

Сз

(Х-Х

)-а

(2-2

)у,

= —/сози + (у

—

Уо)(^ со + Т^т);

\ 2* соз 0) /

д(0

ду

ди

ду

А'="Г~ = 0;

дх„

(х—х

у,

д</ 1

&'=^7~ = -г(г/ —г/о);

д! г

дуо

а.

Таким образом, уравнения поправок можно представить в виде

абх

+ Ь8У

+ сЬ2

+ йЬа + ебш + /бх + §б/ +

И&х,

+ Яуо + (х)—

= о;

а'8Х

+ 6'6К

+ с'Ь2

+ й'бсс + г'бш + /'бх + г'б/ +

+ л'бх

++ (у) — у = о'.

(20.2)

391.

Одна опорная точка дает два уравнения с девятью неизвестными

и весами р и р". Следовательно, для решения задачи необходимо

не менее пяти точек.

Уравнения (20.2) решаются под условием

[ра

+ р V

] = ппп

методом последовательных приближений. Для этого сначала из

меряют координаты опорных точек на снимке. Затем по прибли-

женным значениям элементов ориентирования (начальное прибли-

жение) вычисляют координаты (х) и (у) тех же опорных точек на

снимке и коэффициенты уравнений поправок. Составляют уравне-

ния поправок и нормальные уравнения. Решают нормальные урав-

нения, в результате чего получают поправки к начальному при-

ближению. Введя эти поправки, находят первое приближение не-

известных. Используя первое приближение, вновь вычисляют ве-

личины (х) и (у) и коэффициенты уравнений поправок. Составляют

новые уравнения поправок и нормальные уравнения, в результате

решения которых получают поправки к первому приближению

и второе приближение неизвестных.

Вычисления продолжают до тех пор, пока разность значений

каждого неизвестного в двух последних приближениях не будет

меньше установленного допуска. При подсчете этого допуска учи-

тываются требуемая точность определения элементов ориентирова-

ния, а также точность построения и измерения снимков.

Для оценки точности решения задачи в последнем приближении

вычисляют весовые коэффициенты и поправки V. Находят ошибку

единицы веса

где п — число опорных точек. Затем вычисляют средние квадра-

тические ошибки элементов

23 = I

л/^; = ее;

= ^ У^ЭЭ.

Если элементы внутреннего ориентирования снимка известны

с достаточной точностью, то в уравнениях (20.2) будет только шесть

неизвестных, для определения которых необходимо иметь не менее

трех опорных точек.

Изложенный выше'способ пригоден для снимков с любыми эле-

ментами ориентирования. Если угловые элементы внешнего ориен-

392.

(20.3)

= У^;

(й = и У

= р У^;

(20.4)

тирования малы, то уравнения (20.2) можно представить в таком

виде:

I „„ , * „„ , (

, ^ , ху

?3-2

—

ух

—

б[—х

+ х — (х) = 0-,

(20.5)

4- XX — — 6( — у

+ у

—

(у) = V'.

Задачу и в этом случае решают путем последовательных прибли-

жений, полагая, что в начальном приближении элементы а, со, х,

о>

Уо равны нулю.

Способ, рассмотренный в данном параграфе, позволяет при опре-

делении элементов внешнего ориентирования учесть влияние эле-

ментов внутреннего ориентирования, величины которых в полете

могут отличаться от значений, полученных в лабораторных усло-

виях.

В случае равнинной местности системы уравнений (20.2) и (20.5)

плохо обусловлены и точность определения элементов внутреннего

ориентирования недостаточна.

Способ используется и для решения нетопографических задач,

например, для определения траектории, скорости и колебаний са-

молета и других носителей.

§ 141. Определение элементов ориентирования снимка

по звездам

Рассмотрим способ, позволяющий определить направление глав-

ного луча, угол поворота снимка и элементы внутреннего ориенти-

рования по звездам, изобразившимся на снимке.

На рис. 257: РР' — ось мира; Р — северный полюс мира; |ЗВ —

небесный экватор, у — точка весеннего равноденствия.

Совместим начало прямоугольной системы координат XV2 с

центром 5 небесной сферы, ось 2 — с осью мира, а плоскость XI —

с кругом склонения равноденственных точек.

Пусть при фотографировании звезд с точки 5 оптическая ось

фотокамеры направлена вдоль оси мира. В этом случае плоскость

снимка Р° параллельна плоскости XV. Пусть координатные оси

х° и у

снимка соответственно параллельны осям X и V.

Обозначим через / фокусное расстояние фотокамеры, а через

х° и у

—• координаты изображения а

звезды на снимке Р°. Тогда

можно написать следующие зависимости между экваториальными

координатами звезды и координатами ее изображения:

б = —; 1&а= (20.6)

+" уо

393.

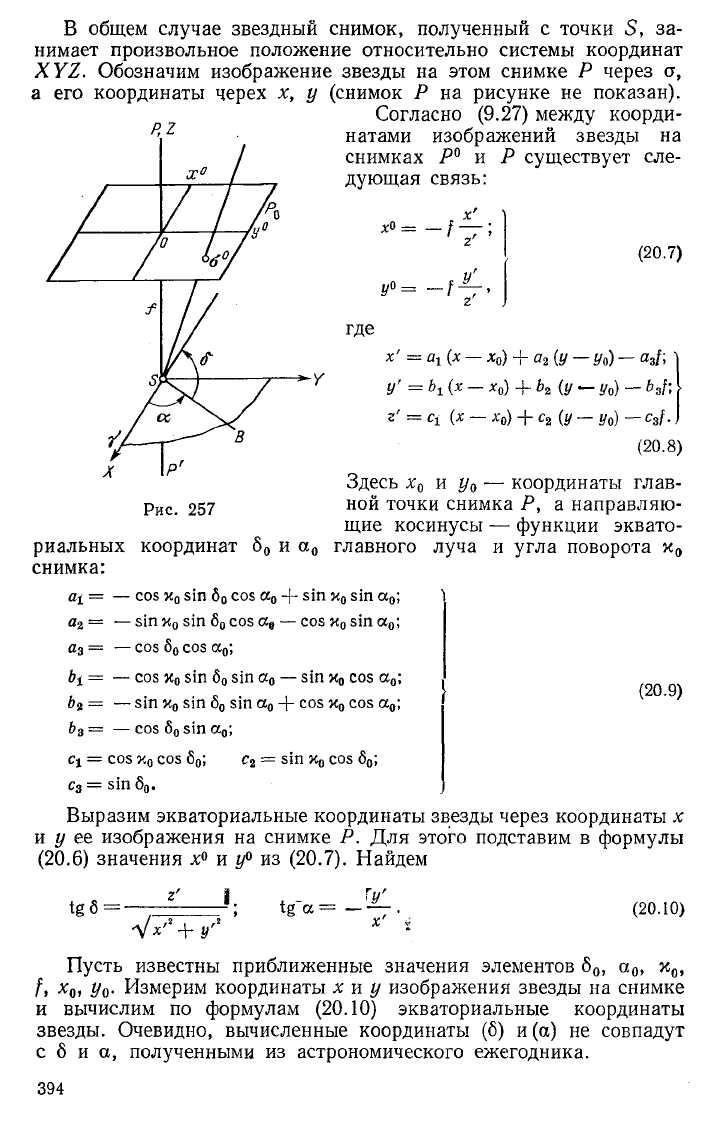
В общем случае звездный снимок, полученный с точки 5, за-

нимает произвольное положение относительно системы координат

ХУ7,. Обозначим изображение звезды на этом снимке Р через с,

а его координаты черех х, у (снимок Р на рисунке не показан).

Согласно (9.27) между коорди-

натами изображений звезды на

снимках Р° и Р существует сле-

дующая связь:

X»

/тг;

(20.7)

где

х' = а

(х — х

) + а

{у — у

) — а

{;

у' =Ь

{х — х

) + Ь

(у — у

) — Ь

(\'

г' = (х — х

) + с

(у — 1/

) — с

]

(20.8)

Здесь х

и у

— координаты глав-

ной точки снимка Р, а направляю-

щие косинусы — функции эквато-

риальных координат 8

и а

главного луча и угла поворота х

снимка:

а±

—

соз х

зт б

соз

«о

+ зт х

зт

ос

;

—

зт х

зт

соз а

—

соз х

зт а

;

—

соз

;

—

соз к

зт

зт а

—

зт х

соз а

;

Ь%

—

зт и

зт б

зт а

+ соз щ соз а

;

—

соз

зт а

;

С\

= соз

у.

соз б

; с

8>п

соз б

;

Сз

= зт б

Выразим экваториальные координаты звезды через координаты х

и у ее изображения на снимке Р. Для этого подставим в формулы

(20.6) значения х° и у

из (20.7). Найдем

(20.9)

г'

+»'

, - V

а =

—

— .

х'

(20.10)

Пусть известны приближенные значения элементов о

, к

х<»

Уо- Измерим координаты х и у изображения звезды на снимке

и вычислим по формулам (20.10) экваториальные координаты

звезды. Очевидно, вычисленные координаты (б) и (а) не совпадут

с б и а, полученными из астрономического ежегодника.

394.

Для определения поправок к приближенным значениям неиз-

вестных напишем

= б = б)

дд

^ а/ '

да

д<

р X I

Ф .

дх

Ф' = {§а = (*8а)

дх

ду

аф'

аб

а®' аф' .

бб

+ —ба

бк

да

дх

аф' . аф' , _дф^_

б / + ——бх

+ -7—6 у

а/

дх

дУо

(20.11)

Частные производные найдем в результате дифференцирования

функций ф и ф':

аф

г' соз б

+ — (*'

СОЗ

+ у'

81П

) б

аф

дао

дф

= 0;

ах

= — с

х —

— — [х' (а

у — а

х) + у' (Ь

у — Ь

х)

1§

б *§б;

аф

д!

дф

дх

аф

(а

х' + Ъ

у') 1§

б -с

_1_

г'

дУй г

аф'

— («!*' +ЬгУ') б —

-V (а

х' + Ъ

у') 1§

б — с

18 в;

1§б;

—

— (зт «о + соз «о а) а;

аб

у'

аф'

аа„

аф'

= _(1+*

а);

А'

••

ах

аф'

— [ (а

у — а

х) а + Ь

у — Ь

х] а;

—

(а

а + Ь

) а;

д( У

дх

дф' 1

/' = = — — {а

+ Ь

) а.

ду

(20.12)

395.

Пусть имеются избыточные измерения. Тогда уравнения (20.11)

можно представить в таком виде:

абб

Ь8а

+ сбх

+ йб/ + е8х

+ /б</

+ I = V,

а'бб

+ 6'ба

+ с'био + й'8[ + е'8х

+ /%

+ /' = о', /

°'

13)

где

/ = (1§б)-1§б; !' = №«) -^а. (20.14)

Одна звезда, изобразившаяся на снимке, дает два уравнения

(20.13) с шестью неизвестными. Таким образом, для решения за-

дачи необходимо не менее трех звезд. Если элементы внутреннего

ориентирования известны и требуется найти только поправки к при-

ближенным значениям элементов внешнего ориентирования снимка,

то задача решается по двум звездам.

Уравнения (20.13) решаются под условием

[рИ

+ р'1/'

] =

ГП1П

методом последовательных приближений.

Для оценки точности решения задачи в последнем приближении

вычисляют весовые коэффициенты (2 и поправки V и г/. Находят

ошибку единицы веса

-- Л/

•

где п — число звезд, использованных для определения элементсв

ориентирования снимка.

Затем вычисляют средние квадрэтические ошибки неизвестных

= ц д/Сп; т[ = ц у (?

;

д/С*

; т

Хо

= д/р

5б

; (20.16)

*о

У ; Щ

Сое •

Изложенные выше способы определения элементов ориентиро-

вания по опорным точкам и по звездам используются и для выявле-

ния систематических ошибок снимка. В этом случае в уравнения

поправок вводят дополнительные параметры в виде полиномов

различных степеней, например полином (4.41), увеличивая соот-

ветственно количество опорных точек или звезд. Решив уравне-

ния, получают элементы ориентирования снимка и коэффициенты

полинома, позволяющие исключить систематические ошибки из

результатов измерений.

§ 142. Определение углов наклона снимка

по линии горизонта

Этот способ основан на применении дополнительной камеры,

жестко связанной с основной камерой и предназначенной для фо-

тографирования горизонта. Затворы обеих камер работают синх-

ронно.

396.

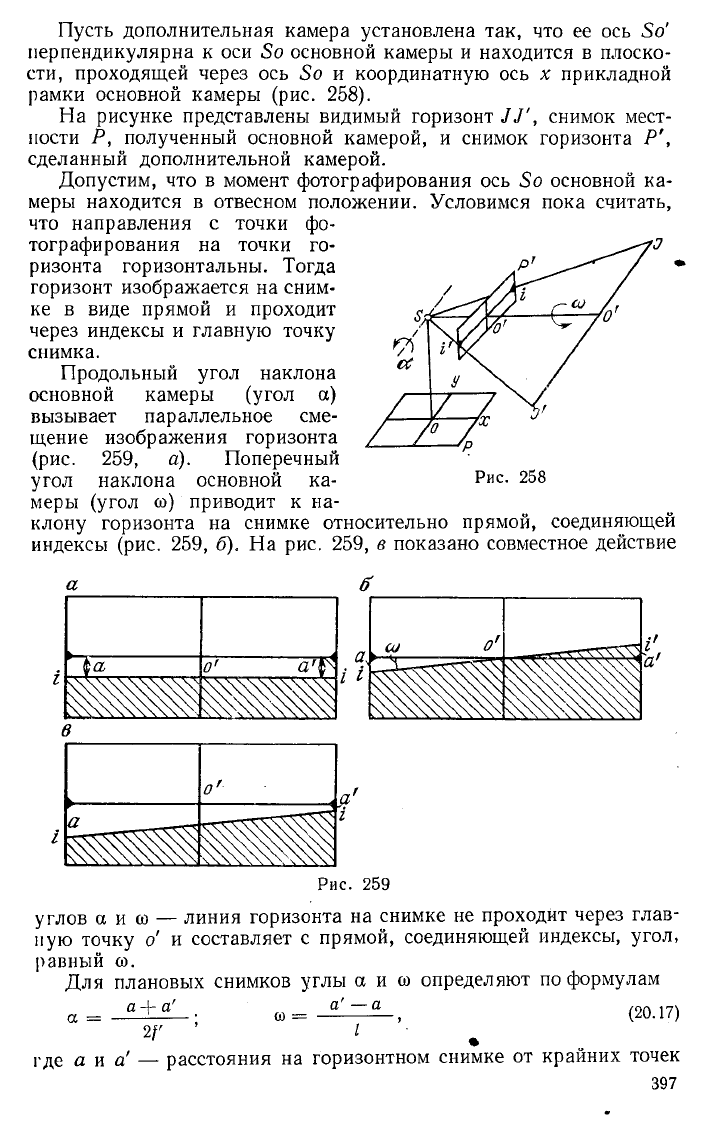
Пусть дополнительная камера установлена так, что ее ось 5о'

перпендикулярна к оси 5о основной камеры и находится в плоско-

сти, проходящей через ось Зо и координатную ось х прикладной

рамки основной камеры (рис. 258).

На рисунке представлены видимый горизонт ]]', снимок мест-

ности Р, полученный основной камерой, и снимок горизонта Р',

сделанный дополнительной камерой.

Допустим, что в момент фотографирования ось Зо основной ка-

меры находится в отвесном положении. Условимся пока считать,

что направления с точки фо-

тографирования на точки го-

ризонта горизонтальны. Тогда

горизонт изображается на сним-

ке в виде прямой и проходит

через индексы и главную точку

снимка.

Продольный угол наклона

основной камеры (угол а)

вызывает параллельное сме-

щение изображения горизонта

(рис. 259, а). Поперечный

угол наклона основной ка-

меры (угол со) приводит к на-

клону горизонта на снимке относительно прямой, соединяющей

индексы (рис. 259, б), На рис. 259, в показано совместное действие

Рис. 258

СО о'

цц

8111

а'

Рис. 259

углов а и со — линия горизонта на снимке не проходит через глав-

ную точку о' и составляет с прямой, соединяющей индексы, угол,

равный со.

Для плановых снимков углы а и со определяют по формулам

аа' а'—а

2/'

со

(20.17)

где а и а' — расстояния на горизонтном снимке от крайних точек

397

горизонта I и Г до прямой, проходящей через индексы; /' — фокус-

ное расстояние дополнительной камеры; / — длина горизонтного

снимка.

Величина а считается положительной, если точка I находится

выше линии индексов.

Угол со, вычисленный по формуле (20.17), непосредственно

представляет поперечный наклон основного снимка, а в угол а

следует ввести поправки за наклон видимого горизонта и кривизну

Земли.

На рис. 260: О — центр Земли; 5 — точка фотографирования,

высота которой Я = 55

; В — точка действительного горизонта;

"т

— угол наклона истинного горизонта. Вследствие земной реф-

ракции наблюдатель, находящийся в точке 5, видит горизонт при-

поднятым над точкой В на угол у. На горизонтном снимке зафикси-

руется не горизонтальное на-

правление 8к, как предполага-

лось выше, а наклонное 8В',

представляющее собой касатель-

Рис. 260 Рис. 261

ную к лучу в точке 5. Угол т между направлениями 8В' и Зк

называется углом наклона видимого горизонта. Как следует из

рисунка,

т = т

—

V-

Для угла т

напишем

, 5в У(Д + Щ* — Я

/ 2Н / Н у

1§т

°= = Л/я

(т) •

где К = 6370 км — средний радиус Земли.

Высота Я мала сравнительно с Поэтому можно считать, что

2Н

Угол у получен из непосредственных наблюдений:

У = Лт

где к — коэффициент земной рефракции.

398.

Следовательно,

т = т

—

6т

— к) т

или

т =

—щ-у/ънт. (20.18)

Под влиянием кривизны Земли горизонт изображается на снимке

не прямой линией, а в виде дуги. При измерении величин а на го-

ризонтном снимке вместо касательной к дуге горизонта в средней

ее части обычно пользуются секущей линией. Поэтому в угол а,

полученный по формуле (20.17), следует ввести еще поправку сг

за кривизну Земли (рис. 261).

Пусть 5 — точка фотографирования; / и /' — точки горизонта,

которые изображаются на краях снимка; О — центр Земли. Оче-

видно, что

а = к! О,

где к — высота кругового сегмента; О — дальность видимого го-

ризонта.

Величина

к = Я — Я соз

= 2/? 5Ш

—

да

— ЯЬ

2 2

где б •— центральный угол.

Обозначив через угол зрения горизонтной камеры, можно

написать

2 Я Я 2

Следовательно,

1 п

+ 2

а= *§

—р.

2 Я 2

Дальность видимого горизонта

(20.19)

КМ

= 3,80У//

. (20.20)

Вероятно, угол наклона видимого горизонта т не является по-

стоянной величиной для всех направлений на горизонт из данной

точки фотографирования, так как атмосферные условия, которые

влияют на рефракцию, нельзя считать однородными по всему го-

ризонту.

Эти изменения угла т целиком сказываются на определении

угла айв меньшей мере на определении угла со.

Чтобы освободиться от поправок т и а, фотографируют гори-

зонт в двух взаимно перпендикулярных направлениях. В этом слу-

чае основная камера имеет две дополнительные камеры, которые

фотографируют горизонт вдоль полета и перпендикулярно к нему.

Угол со находят по снимку, полученному вдоль полета, а угол а —

по снимку, полученному перпендикулярно к линии полета.

399.