Lin S.D. Water and Wastewater Calculations Manual

Подождите немного. Документ загружается.

Step 2. Determine DO saturation value

From Table 1.2, or by calculation, for C

at 24.8⬚C this is

⫽ 8.21 mg/L

Step 3. Compute C

Since

r ⫽ (C

– C

)/(C

– C

)

therefore

17.2 Inﬂuence of tributaries

Tributary sources of DO are often an important contribution in deriv-

ing a DO balance in stream waters. These sources may be tributary

streams or outfalls of wastewater treatment plants. A tributary con-

tribution of DO

can be computed based on mass balance basis of DO,

ammonia, and BOD values from tributaries. The downstream effect

of any DO input is determined by mass balance computations: in

terms of pounds per day the tributary load can simply add to the

mainstream load occurring above the confluence. The following two

examples are used to demonstrate the influence of tributary sources

of DO. Example 1 involves a tributary stream. Example 2 involves the

design of an outfall structure to achieve a minimum DO at the point

of discharge.

Example 1: Given: Tributary flow Q

⫽ 123 cfs

Tributary DO ⫽ 6.7 mg/L

Mainstream flow Q

⫽ 448 cfs

Mainstream DO ⫽ 5.2 mg/L

Find: DO concentration and DO load at the confluence.

solution:

Step 1. Determine DO concentration

Assuming there is a complete mix immediately below the confluence, the DO

concentration downstream on the confluence can be determined by mass

balance.

5 5.14 smg/Ld

5 8.21 2 3.07

5 8.21 2 s8.21 2 3.85d/1.42

5 C

2 sC

2 C

d/r

Streams and Rivers 95

Step 2. Compute DO loadings

Since

Note: The factor 5.39 is the same as that in Eq. (1.91).

Similarly,

Example 2: The difference in elevation between the outfall crest and the 7-day,

10-year low flow is 4.0 ft (1.22 m). Utilizing this head difference, determine if a

free-falling two-step weir at the outfall will insure a minimum DO of 5.0 mg/L

at the point of discharge. The flow of wastewater effluent and the stream are,

respectively, 6.19 and 14.47 cfs (175 and 410 L/s, or 4 and 10 MGD). DO for the

effluent and stream are 1.85 and 6.40 mg/L, respectively. The temperature of

the effluent is 18.9⬚C. The stream is less than moderately polluted. Determine

the stream DO at the point of effluent discharge and the oxygen balance.

solution:

Step 1. The water quality correction factor is selected as q ⫽ 1.1

5 16,999 slb/dd

Total DO load 5 4442 lb/d 1 12,557 lb/d

5 12,557 slb/dd

Mainstream load 5 5.39 3 5.2 3 448

5 4442 lb/d

Tributary load 5 5.39 3 6.7 3 123

or 5 5.39 lb/sd

mg/L

cfsd 3 DO mg/L 3 Q cfs

5 5.39 3 DO 3 Q lb/d

5 28.32 3 DO 3 Qa

1 lb

454,000 mg

86,400 s

5 DO 3 Qa

3 cfs 3 28.32

L/s

cfs

DO load 5 sDO, mg/Ld 3 sQ, cfsd

5 5.5 smg/Ld

5 s123 3 6.7 1 448 3 5.2d/s123 1 448d

DO 5

3 DO

1 Q

3 DO

1 Q

96 Chapter 1

b ⫽ 1.3 for free-fall step-weir

⫽ 9.23 mg/L, when T ⫽ 18.9⬚C from Table 1.2

⫽ 1.85 mg/L as effluent DO

h ⫽ 4.0 ft

Step 2. Determine r with the channel dam reaeration model

Step 3. Compute C

Note: C

is the effluent DO as it reaches the stream.

Step 4. Compute the resultant DO in the stream

Assuming there is a complete mixing with the stream water, the resultant DO

at the point of discharge is

Step 5. Calculate oxygen mass balance

DO load in stream above the point of effluent discharge

The total amount of oxygen below the point of discharge is 694 (195 ⫹ 499) lb/d.

5 499 slb/dd

5 5.39 3 6.40 3 14.47

5 5.39 3 DO 3 Q

5 195 slb/dd

5 5.39 3 5.85 3 6.19

DO load from effluent 5 5.39 3 DO 3 Q

5 6.23 smg/Ld

DO 5

5.85 3 6.19 1 6.40 3 14.47

6.19 1 14.47

5 5.85 smg/Ld

5 9.23 2 s9.23 2 1.85d/2.18

5 C

2 sC

2 C

d/r

r 5 sC

2 C

d/sC

2 C

5 2.18

5 1 1 0.11 3 1.1 3 1.3s1 1 0.046 3 18.9d 3 4

r 5 1 1 0.11qbs1 1 0.046Tdh

Streams and Rivers 97

17.3 DO used

The term DO

used

(DO

) in Eq. (1.111) represents the oxygen consumed

biologically within a stream reach. This term can be determined by

three methods (Butts et al., 1973): (1) observed DO concentrations in con-

junction with reaeration estimate; (2) bottle BOD and deoxygenation

rate determinations of river water samples; and (3) long-term bottle

BOD progression evaluation of a wastewater effluent. The method used

will probably be dictated by the existing data or the resources available

for collecting usable data.

The term DO

includes DO usage due to carbonaceous and nitrogenous

BOD and to SOD, as stated previously. The ratio of DO contribution by algal

photosynthesis to DO consumption by algal respiration is assumed to be

unity, although it can handle values greater or less than one when derived

on a diurnal basis. For a series of stream reaches, each incremental DO

value is added and the accumulated sums, with the corresponding time of

travel in the stream, are fitted to the first-order exponential expression

(1.120)

where y ⫽ oxygen demand exerted (DO

)

⫽ ultimate oxygen demand, including carbonaceous and

nitrogenous

⫽ in-stream deoxygenation coefficient to the base e, per day

t ⫽ time of travel, days

Note: The coefficient K

is comparable to the composite of the terms K

and K

previously defined in the discussion regarding the conceptual

approach to waste-assimilative analysis.

The use of field DO values in estimating the waste-degradation char-

acteristics of a stream has certain advantages: the need for laboratory

BOD tests is eliminated which saves time and cost; the reliability of the

results should be better since the measurement of DO is far more precise

and accurate than the BOD test; also, stream measured DO concentrations

take into account the in situ oxygen demand in the stream, which includes

both dissolved and benthic demand, whereas laboratory BOD results gen-

erally reflect only the oxygen demand exerted by dissolved matter.

Estimations of K

and L

. The data obtained from steam survey, a sum-

mation of DO

values and corresponding time of travel t at an observed

water temperature, have to be computed along the reach of a stream.

Nowadays, for determinations of K

and L

, one can simplify the calcu-

lation by using a computer or a programmable calculator. However, the

following example illustrates the use of the Thomas slope method for

determining K

and L

y 5 L

s1 2 e

98 Chapter 1

17.4 Procedures of pragmatic approach

The steps of the pragmatic approach involved in estimating the waste-

assimilative capacity of a stream based upon a pragmatic approach can

be summarized as follows (Butts et al., 1973):

1. Develop a full understanding of the stream length, its channel geom-

etry, water stage and flow patterns, and the general hydrologic fea-

tures of the watershed.

2. Determine the 7-day, 10-year flow of the stream and select a design

water temperature.

3. Define the location of all dams and their physical features; define

also the location of all tributary flows and relevant data regarding

them.

4. Divide the stream into reaches consistent with significant changes

in cross sections and determine the volumes and average depth in

each reach.

5. At the beginning and end of each reach, during low-flow conditions

and summer temperatures, undertake a series of field determina-

tions for at least water temperature and DO concentrations and, if

desired, collect water samples for BOD determinations.

6. Compute the time of travel within each reach at stream flows

observed during the time of sampling as well as that during 7-day,

10-year low flow.

7. From the observed DO values, flow, and time of travel, compute

– DO

, as demonstrated in Table 1.17 (see later).

8. Select DO saturation values from Table 1.2 for observed stream

temperature conditions, and compute the natural reaeration for

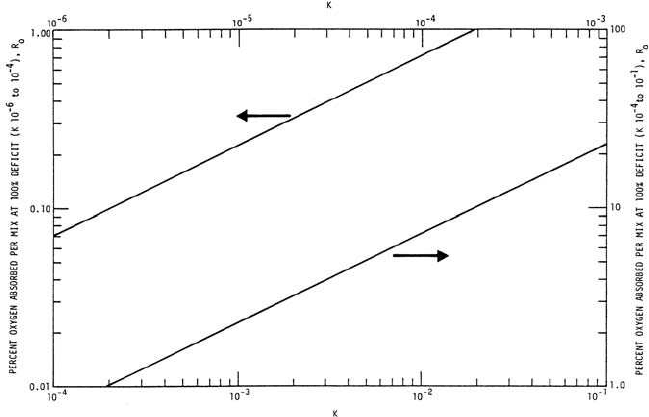
each reach using Figs. 1.12 and 1.13 in conjunction with appropri-

ate equations for finding the mix time M and the percent absorption

at 100% deficit R

. They are determined as the same manner of the

example in Section 16.2. Keep in mind the need to make adjustments

in accordance with weir and mass balance formulas where dams and

tributaries are encountered.

9. Calculate, by summation, the DO

for each reach as demonstrated

in Table 1.18 (see later).

10. From an array of the DO

versus t data, determine L

and K

preferably by the methods of Read–Theriault, steepest descent,

or least squares. For a graphical solution, the Thomas slope

method is satisfactory. Adjust the values for L

and K

for the

selected design water temperature by the use of Eqs. (1.26) and

(1.28).

Streams and Rivers 99

11. Apply the removal efficiency anticipated to the computed ulti-

mate oxygen demand L

and develop the required expression DO

⫽

(1 – e

–Kt

12. From the values developed in step 6 for time of travel and depth at

7-day, 10-year low flow, use the observed DO just upstream of the

discharge point (D

at the beginning of the reach) as a starting-

point, and follow the computation.

13. Note whether or not the removal efficiency selected will permit pre-

dicted DO concentrations in the stream compatible with water qual-

ity standards.

Example: A long reach of a moderately sized river is investigated. There is

an overloaded secondary wastewater treatment plant discharging its efflu-

ent immediately above sampling station 1 (upstream). The plant, correctly,

has BOD removal efficiency of 65%. A total of 12 sampling stations are estab-

lished in reaches of the study river. Downstream stations 3 and 4 are above

and below an ogee channel dam, respectively. Stations 10 and 11 are imme-

diately above and below the confluence of the main stream and a tributary

which has relatively clean water. The 7-day, 10-year low flow of the main

receiving stream and the tributary are 660 and 96 cfs, respectively. The design

water temperature is selected as 27⬚C.

A stream field survey for flow, water temperature, DO, average depth, and

time of travel is conducted during summer low-flow conditions. During the

100 Chapter 1

Figure 1.13 Modified Velz curve (Butts et al., 1973).

field survey, the receiving stream in the vicinity of the effluent discharge was

822 cfs and the tributary flow was 111 cfs. The DO values are 5.96 and 6.2

mg/L, respectively. Data obtained from field measurements and subsequent

computations for DO values are presented in Tables 1.16, 1.17, and 1.18. The

DO levels in the stream are not less than 5.0 mg/L, as required.

Question: Determine the DO concentrations along the reach of the stream at

design temperature and design flow conditions, if the efficiency of sewage

treatment plant is updated to at least 90% BOD removal.

Answer: The solution is approached in two sessions: (1) the deoxygenation

rate coefficients K

and L

should be determined under the existing condi-

tions; this involves steps 1 to 5; (2) a predictive profile of DO concentrations

will be calculated under 7-day, 10-year low flow and 27ºC design conditions

(steps 6 and 7).

solution:

Step 1. Compute DO values

In Table 1.16, data are obtained from fieldwork and subsequent DO compu-

tations for other purposes. The term DO

⫺ DO

(lb/d) will be used in the equa-

tion for Table 1.18. A plot of DO measured and time of travel t can be made

(not shown). It suggests that a profound DO sag exists in the stream below

the major pollution source of effluent discharge.

Step 2. Compute the natural reaeration, DO

In Table 1.17, values of saturated DO (DO

) at the specified water tempera-

ture are obtained from Table 1.2. The values of M and R

are taken from Figs.

1.12 and 1.13 on the basis of the physical dimension of the stream listed in

Table 1.16 or calculated from Eq. (1.114) (M ⫽ 13.94 In H ⫺ 745).

Step 3. Calculate DO used, DO

The DO

is calculated from equation DO

⫽ (DO

⫺ DO

) ⫹ DO

⫹ DO

Without consideration of DO

, the values of DO

for each reach of the stream

are given in Table 1.18. It should be noted that DO

does not apply yet.

Step 4. Determine K

d(23)

and L

d(23)

for T ⫽ 23ºC (during the field survey)

Using the Thomas (1950) slope method, the factor (⌺t/⌺DO

)

1/3

is plotted

on arithmetic graph paper against ⌺t as shown in Fig. 1.14. A line of best

fit is then drawn, often neglecting the first two points. The ordinate inter-

cept b is read as 0.0338; and the slope of the line S is computed as 0.00176

[i.e. (0.0426 ⫺ 0.0338)/5]. The determine K

and L

at 23ºC.

5 83,500 slb/dd

as23d

5 1/sK

d 5 1/s0.31 3 0.0338

ds23d

5 6S/b 5 6 3 0.00176/0.0338 5 0.31 sper dayd

Streams and Rivers 101

The curve is expressed as

Step 5. Compute K

d(27)

and L

a(27)

for design temperature 27⬚C

Using Eq. (1.26)

Similarly, using Eq. (1.28)

Next step goes to design phase.

5 89,800 slb/dd

5 83,500 3 1.14/1.06

as27d

5 L

as23d

3 s0.6 1 0.02 3 27d/s0.6 1 0.02 3 23d

asT d

5 L

as20d

3 s0.6 1 0.02T d

5 0.37 sper dayd

5 0.31 3 1.3792/1.1477

ds27d

5 K

ds23d

3 1.047

/1.047

ds23d

5 K

ds20d

3 1.047

23220

ds27d

5 K

ds20d

3 1.047

27220

y 5 83,500s1 2 e

20.31t

102 Chapter 1

TABLE 1.16 Field Data and DO Computations

Flow, cfs DO

observed

†

DO averaged

⫺ DO

Station at station mean mg/L lb/d

∗

lb/d mg/L lb/d

1 822 5.96 26406

2 830 826 3.44 15390 11016 4.70 20925

3 836 833 2.40 10814 4575 2.92 13110

Dam

4 836 3.96 17844

5 844 840 3.90 17741 103 3.93 17793

6 855 849 3.70 17051 690 3.80 17389

7 871 863 3.60 16900 151 3.65 16978

8 880 875 3.90 18498 ⫺1598 3.75 17686

9 880 880 4.04 19163 ⫺665 3.97 18831

10 888 884 4.44 21251 ⫺2288 4.27 20202

Tributary

11 999 5.18 27892 ⫺6641 4.81 24474

12 1010 1005 5.28 28743 ⫺851 5.23 28330

∗

DO (lb/d) ⫽ 5.39 ⫻ flow (cfs) ⫻ DO (mg/L).

†

at the end of a reach is the DO

of that reach.

TABLE 1.17 Computations of Natural Reaeration

Temp, DO

Mean D

, Mean D

†

, Depth h, M, t⬘, 5.39Q ⫻ DO

∗

Station ºC mg/L mg/L mg/L ft min min lb/d lb/d

1 22.8 8.53

2 22.9 8.52 8.53 4.70 6.6 18.8 846.7 0.449 0.0042 45.0 37977 3225

3 23.0 8.50 8.51 2.92 6.8 19.4 1201.0 0.657 0.0041 61.9 38209 6370

4 23.0 8.50

5 23.0 8.50 8.50 3.93 2.9 4.4 396.0 0.538 0.0046 90.0 38485 8566

6 23.1 8.48 8.49 3.80 3.8 11.2 792.0 0.552 0.0052 70.7 38851 7892

7 23.1 8.48 8.48 3.65 5.2 15.5 1591.2 0.57 0.0049 102.7 39445 11301

8 23.2 8.46 8.47 3.75 6.1 17.6 1630.0 0.557 0.0045 92.6 39946 9277

9 23.2 8.46 8.46 3.97 6.3 18.2 1118.9 0.531 0.0044 61.5 40127 5761

10 23.3 8.45 8.46 4.24 6.5 18.6 911.5 0.499 0.0043 49.0 40310 4237

11 23.1 8.48 8.47 4.81 0.432

12 23.1 8.48 8.48 5.23 7.2 19.9 656.6 0.383 0.0040 33.0 45936 2324

∗

and it is calculated as the same manner of Example in Section 16.2.

†

Mean D

is from Table 1.16.

5 a1 2

100

ba5.39Q 3 DO

100

1 2

103

104 Chapter 1

TABLE 1.18 Calculation of DO Used

t, ⌺t, DO

⫺ DO

,DO

∗

⌺DO

Station days days lb/d lb/d lb/d lb/d (⌺t/⌺DO

)

1/3

2 0.588 0.588 11016 3225 14241 14241 0.03456

3 0.834 1.422 4575 6370 10945 25186 0.03836

4 25186

5 0.275 1.697 103 8566 8669 33855 0.03687

6 0.550 2.247 690 7892 8582 42437 0.03755

7 1.105 3.352 151 11301 11452 53889 0.03962

8 1.132 4.484 ⫺1598 9277 7679 61568 0.04176

9 0.777 5.261 ⫺665 5761 5096 66664 0.04289

10 0.633 5.894 ⫺2888 4237 1349 68013 0.04425

11 68013

12 0.456 6.350 ⫺851 2324 1473 69486 0.04504

∗

⫽ DO

⫺ DO

⫹ DO

Step 6. Calculate the design BOD loading after plant improvement

Since the current overloaded wastewater treatment plant only removes 65%

of the incoming BOD load, the raw wastewater BOD load is

89,800 lb/d/(1 ⫺ 0.65) ⫽ 256,600(lb/d)

The expanded (updated) activated-sludge process may be expected to remove

90% to 95% of the BOD load from the raw wastewater. For the safe side, 90%

removal is selected for the design purpose. Therefore, the design load L

27⬚C to the stream will be 25,660 lb/d (256,600 ⫻ 0.1).

Step 7. Gather new input data for DO profile

In order to develop the predictive profile for DO concentration in the receiv-

ing stream after the expanded secondary wastewater treatment plant is func-

tioning, the following design factors are obtained from field survey data and

the results computed:

Stream flow ⫽ 660 cfs At the dam q ⫽ 1.1

Tributary flow ⫽ 96 cfs b ⫽ 0.58

Tributary DO ⫽ 6.2 mg/L h ⫽ 6.1 ft

DO at station 1 ⫽ 5.90 mg/L K

d(27)

⫽ 0.37 per day

Water temperature ⫽ 27⬚C L

a(27)

⫽ 25,660 lb/d

H and t are available from cross-sectional data.

Step 8. Perform DO profile computations

Computations are essentially the same as previous steps with some minor

modifications (Table 1.19).