Li S.Z., Jain A.K. (eds.) Encyclopedia of Biometrics

Подождите немного. Документ загружается.

In contrast to LDA, the decision boundaries of QDA

are quadrat ic, which is resulted from the assump-

tion on the different covariance matrices. From the

added ﬂexibility obtained from the quadratic decision

boundaries, QDA often outperforms LDA when the

size of training data is ver y large. However, when

the size of the training set D is small compared to the

dimension D of the feature space, the large number of

parameters of QDA relative to LDA causes over-ﬁtting

or ill-posed estimation for the estimated covariance

matrices. To solve this problem, various regularization

or Bayesian techniques have been proposed to obtain

more robust estimates:

1. Regularized discriminant analysis (RDA) [7, 8]

employs the regularized form of covariance matri-

ces by shrinking S

of QDA towards the common

covariance matrix S of LDA, that is, S

(a) ¼ aS

(1a)S for a 2 [0, 1]. Additionally, the common

covariance matrix S could be shrunk towards

the scalar covariance, S(g) ¼ gSþ(1g)s

I for g

2[0, 1]. The pair of parameters is selected by cross-

validation based on the classiﬁcation accuracy of

the training set.

2. Leave-one-out covariance estimator (LOOC) [9]

ﬁnds an optimal regularized covariance matrices

by mixing four different covariance matrices of

,diag(S

), S, and diag(S), where the mixing

coefﬁcients are determined by maximizing the

average leave-one-out log likelihood of each class.

3. Bayesian QDA introduces prior distributions over

the mean m

and the covariance matrices S

[10], or

over the Gaussian distributions themselves [11].

The expectations of the class-conditional densities

are calculated analytically in terms of the para-

meters. The hyper-parameters of the prior distribu-

tions are chosen by cross-validation.

Naive Bayes Classifier

In the naive Bayes classiﬁer, the conditional indepen-

dence assumption makes the factorized class-condi-

tional densities of the form

pðxjC

Þ¼

i¼1

pðx

Þ: ð8Þ

The compone nt densities pðx

Þ can be modeled

with various parametric and nonparametric distribu-

tions, including the following:

1. For continuous features, the component densities

are chosen to be Gaussian. In this case, the naive

Bayes classiﬁer is equivalent to QDA with diagonal

covariance matrices for each class.

2. For discrete features, multinomial distributions are

used to model the component densities. The mul-

tinomial assumption makes a

(x) and the resulting

decision boundaries to be linear in x.

3. The component densities can be estimated using

one-dimensional kernel density or histogram esti-

mates for non-parametric approaches.

The naive Bayes model assumption is useful when the

dimensionality D of the feature space is very high,

making the direct density estimation in the full feature

space unreliable. It is also attractive if the feature vector

consists of heterogeneous features including continu-

ous and discrete features.

Nonparametric Approaches

One major problem of parametric approaches is that

the actual class-conditional density is not a linear nor a

quadratic form in many real-world data. It causes the

poor classiﬁcation performance, since the actual distri-

bution of data is different from a functional form we

speciﬁed, regardless of parameters.

To solve this problem, one can increase the ﬂexibility

of the density model by adding more and more para-

meters, leading to a model with inﬁnitely man y num-

ber of parameters, called nonparametric density

estimation. Otherwise, rather than modeling the

whole distribution of a class, one can model only a

decision boundary that separates one class from the

others, since restricting the func tional form of the

boundary is a weaker assumption than restricting

that of the whole distribution of data. Either using a

nonparametric density model or modeling a decision

boundary are called nonparametric approaches. In this

article, the latter approach is only considered.

We deﬁne a function a

(x) as a relevancy score of

x for C

, such that a

(x) > 0ifx is more likely to be

assigned to C

, and a

(x) < 0 otherwise. Then, the

surface a

(x) ¼ 0 represents the decision boundary

1300

Supervised Learning

between C

and the other classes, and a test point x is

assigned to C

if k ¼ arg max

(x), which is called

one-against-all.

Many nonparametric methods have been derived

from various models for a

(x). We introduce three

representative methods [12, 13, 14] (see Table 2):

1. k-nearest neighbor algorithm (k-NN) chooses k

data points in the training set, which are closest

from x, then a

(x) is the number of those selected

points belonging to C

2. Artiﬁcial neural networks (ANNs) represent a

(x)

as a multilayered feed-forward network. The ℓth

layer consists of W

ℓ

nodes, where the jth node in

the layer sends a (non)linear function value f

(ℓ)

(x)

as a signal to the nodes in the (L þ 1)th layer. Then,

(x) is the signal of the kth node in the ﬁnal layer,

(Lþ1)

(x).

3. Support vector machines (SVMs ) choose some

‘‘important’’ training points, called support vectors,

then represent a

(x) as a linear combination of

them. SVM is known to be the best supervised

learning method for most real-world data.

k-Nearest Neighbor Algorithm

Given a set of data points X ¼ {x

, ...x

} and a set

of the corresponding labels Y ¼ {y

, y

}, K-NN

assigns a label for a test data point x by majority voting,

that is to choose the most frequently occurred label

in {y

(1)

, y

(2)

, ...y

(k)

}, where x

(i)

denotes the ith nearest

point of x in X and y

(i)

is the label of x

(i)

. That is,

we have

ðxÞ¼jfx

ðiÞ

gj; ð9Þ

where jj denotes the number of elements in a set. The

decision bound ary is not restricted to a speciﬁc func-

tional form. It depends only on the local distribution

of neighbors and the choice of k. Larger k makes the

decision boundary more smooth.

k-NN is widely used in biometrics, especially for

computer vision applications such as face recogni-

tion and pose estimation, where both the number of

images N and dimension of data D are quite large.

However, traditional k-NN takes O(ND) time to com-

pute distances between a test point x and all training

points x

, ...,x

, which is too inefﬁcient for practical

use. Thus, extensive research has focused on fast

approximations based on hashing, embedding or

something [15].

Artificial Neural Networks

In ANNs, the signal of the jth node in the (ℓ þ1)th

layer is determined by the signals from the ℓth layer:

ð‘þ1Þ

ðxÞ¼g w

ð‘Þ>

ð‘Þ

ðxÞþw

ð‘Þ



; ð10Þ

where w

‘

¼½w

ð‘Þ

; w

ð‘Þ

; ; w

ð‘Þ

‘



and f

ð‘Þ

ðxÞ¼

½f

ð‘Þ

ðxÞ; f

ð‘Þ

ðxÞ;  ; f

ð‘Þ

‘

ðxÞ

. The input layer,

(0)

(x), is simply x. g() is a nonlinear, nondecreasing

mapping, causing ANNs to yield a nonlinear decision

boundary. There are two popular mappings: (1) sig-

moid, g(x) ¼1 ∕(1þexp{x}); (2) hyperbolic tangent,

g(x) ¼ tanh(x).

More nodes and layers increase the nonlinearity of

decision boundary obtained by ANNs. However, it is

difﬁcult to train ANNs having a number of nodes and

layers, since the model can easily fall into poor solu-

tions, called local minima.

Radial basis function (RBF) networks [16] are

another type of ANNs, having the form

ðxÞ¼w

FðxÞþw

: ð11Þ

That is, RBF networks contain only one hidden layer,

denoting by F(x)¼[f

(x),f

(x),...,f

(x)], and the

network output is simply a linear combination of the

hidden nodes. The main difference between RBF net-

works and ANNs with L ¼ 1 is the map ping from the

Supervised Learning. Table 2 Comparison among non-parametric methods for classification

Method a

(x)

Number of parameters Decision boundary

k-NN jfx

ði Þ

gj k Nonlinear

ANNs f

(Lþ1)

(x)

‘¼0

ðW

‘

þ 1ÞW

‘

þ 1 Linear (L¼0) or nonlinear (L>0)

SVMs

kðx

; xÞ O(KN) Linear (k(x

,x)¼x

x) or nonlinear (otherwise)

Supervised Learning

1301

input to the hidden. In RBF networks, each j

()isa

nonlinear function similar to Gaussian density:

ðxÞ¼exp b

jjx  c

; ð12Þ

for some b

> 0 and the center vector c

. That is, each

hidden node represents local region whose center is c

and its signal would be stronger if x and c

are closer. In

general, c

is ﬁxed to one of the training points and b

chosen by hand, thus the global optimum of w

and

can be simply found by least squares ﬁtting.

Support Vector Machines

Similar to RBF networks, SVMs obtain a linear decision

boundary in a transformed space: a

(x)¼w

F(x)þ

, where F ( ) is an arbitrary mapping, either linear

or nonlinear. The difference betwen SVMs and ANNs

is the optimality of the decision boundary. In SVMs,

the optimal decision boundary is such that the distance

between the bound ary and the closest point from that

boundary, called the margin, is maximized:

max

min

ðx

Þj

jjw



: ð13Þ

This optimization problem always converges to the glob-

al solution, the maximum margin boundary. Figure 1

shows the motivation for SVMs intuitively. One can

expect that the generalization error of the maximum

margin boundary is less than that of other boundaries.

Theoretically, the generalization power of SVMs is

guaranteed by Vapnik–Chervonenkis theory [17].

Training SVMs can be rewritten as the following

convex optimi zation problem

min

jjw

jj; subject to y

ðx

Þ1 for all i;

ð14Þ

where y

¼ 1ifx

and otherwise1. At the

optimum, a

(x) has the form

ðxÞ¼

i¼1

Fðx

FðxÞ; ð15Þ

where a

 0 is a Lagrangian multiplier of the ith

constraint, y

)  1. If a data point x

is exactly

on the margin, i.e., y

) ¼ 1, then x

is called

support vector and a

> 0. Otherwise, a

¼ 0 and

) > 1. Hence, a

(x) only depends on the sup-

port vectors. To compute F(x

)

F(x), we can intro-

duce a function of the form k(x

, x), representing the

inner product in the feature space can be used, without

computing the mapping F() explicitly. Such a func-

tion is called kernel function [18]. There are two popu-

lar kernel functions: (1) polynomial kernel, k(x

, x)¼

xþc)

for some c and p > 0; (2) Gaussian kernel

(also called as RBF kernel), kðx

; xÞ¼expf

jjx

 xjj

g for some s > 0.

Various algorithms and implementations have been

developed to train SVMs efﬁciently. Two most popular

softwares are LIBSVM [19] and SVM

light

[20], both

Supervised Learning. Figure 1 (Left) Possible solutions obtained by neural networks. (Right) SVMs give one global

solution, the maximum margin boundary.

1302

Supervised Learning

implement several techniques such as working set se-

lection, shrinking heuristics, and LRU caching to speed

up optimization, and provide various kernel functions

with choosing appropriate parameters of those func-

tions automatically (automatic model selection). Two

recent extensions of SVM

light

– SVM

struct

for structured

data, SVM

perf

for training with more than hundred-

thousands of data points – are also popular in

biometrics.

Related Entries

▶ Classiﬁer Design

▶ Machine-Learning

▶ Probability Distribution

References

1. Jain, A.K., Ross, A., Prabhakar, S.: An introduction to biometric

recognition. IEEE Trans. Circuits Syst. Video Technol. 14(1),

4–20 (2004)

2. Jain, A.K., Duin, R.P.W., Mao, J.: Statistical pattern recognition:

A review. IEEE Trans. Pattern Anal. Mach. Intell. 22(1), 4–37

(2000)

3. Duda, R.O., Hart, P.E., Stork, D.G.: Pattern Classiﬁcation. Wiley,

New York (2001)

4. Bishop, C.M.: Pattern Recognition and Machine Learning.

Springer, New York (2006)

5. Hastie, T., Tibsjirani, R., Friedman, J.: The Elements of Statistical

Learning. Springer, New York (2001)

6. Hastie, T., Tibshirani, R.: Discriminant analysis by Gaussian

mixtures. J. R. Stat. Soc. Ser. B 58, 158–176 (1996)

7. Friedman, J.H.: Regularized discriminant analysis. J. Am. Stat.

Assoc. 84, 165–175 (1989)

8. Ye, J., Wang, T.: Regularized discriminant analysis for high

dimensional, low sample size data. In: Proceedings of the ACM

SIGKDD International Conference on Knowledge Discovery and

Data Mining. Philadelphia, PA (2006)

9. Hoffbeck, J.P., Landgrebe, D.A.: Covariance matrix estimation

and classiﬁcation with limited training data. IEEE Trans. Pattern

Anal. Mach. Intell. 18(7), 763–767 (1996)

10. Geisser, S.: Predictive Inference: An Introduction. Chapman &

Hall, New York (1993)

11. Srivastava, S., Gupta, M.R., Frigyik, B.A.: Bayesian quadratic

discriminant analysis. J. Mach. Learn. Res. 8, 1277–1305 (2007)

12. Cover, T., Hart, P.: Nearest neighbor pattern classiﬁcation. IEEE

Trans. Inf. Theory IT–13, 21–27 (1967)

13. Rumelhart, D.E., Hinton, G.E., Williams, R.J.: Learning internal

representations by backpropagating errors. Nature 323, 533–536

(1986)

14. Boser, B.E., Guyon, I., Vapnik, V.N.: A training algorithm for

optimal margin classiﬁers. In: Proceedings of the Fifth Annual

Workshop of Computational Learning Theory, pp. 144–152 (1992)

15. Shakhnarovich, G., Darrell, T., Indyk, P.: Nearest-Neighbor

Methods in Learning and Vision: Theory and Practice. MIT

Press, Cambridge, MA (2006)

16. Moody, J., Darken, C.J.: Fast learning in networks of locally

tuned processing units. Neural Comput. 1, 281–294 (1989)

17. Vapnik, V.N.: The Nature of Statistical Learning Theory.

Springer-Verlag, New York (1995)

18. Scho

lkopf, B., Smola, A.J.: Learning with Kernels. MIT Press,

Cambridge, MA (2002)

19. Chang, C.C., Lin, C.J.: LIBSVM – A Library for Support

Vector Machines, http://www.csie.ntu.edu.tw/~cjlin/libsvm

(2000)

20. Joachims, T.: SVM

light

, http://svmlight.joachims.org (2004)

Supervisor

A generic term for a method or a system that is able to

output an aggregated opinion.

▶ Multiple Experts

Supervisor Opinion

The output of the supervisor which can be a strict score

(0 or 1) or a graded score (2 [0, 1]) representing the

belief of the supervisor on an identit y claim by aggre-

gating expert opinions.

▶ Multiple Experts

Support Vector Machine

MATHIAS M. A DANKO N,MOHAMED CHERIET

University of Quebec ETS, Montreal, Canada

Synonyms

SVM; Margin classiﬁer; Maximum margin classiﬁer ;

Optimal hyperplane

Support Vector Machine

1303

Definition

Support vector machines (SVMs) are particular linear

▶ classiﬁers which are based on the margin maximiza-

tion principle. They perform

▶ structural risk minimi-

zation, which improves the complexity of the classiﬁer

with the aim of achieving excellent

▶ generalization

performance. The SVM accomplishes the classiﬁcation

task by constructing, in a higher dimensional space, the

hyperplane that optimally separates the data into two

categories.

Introduction

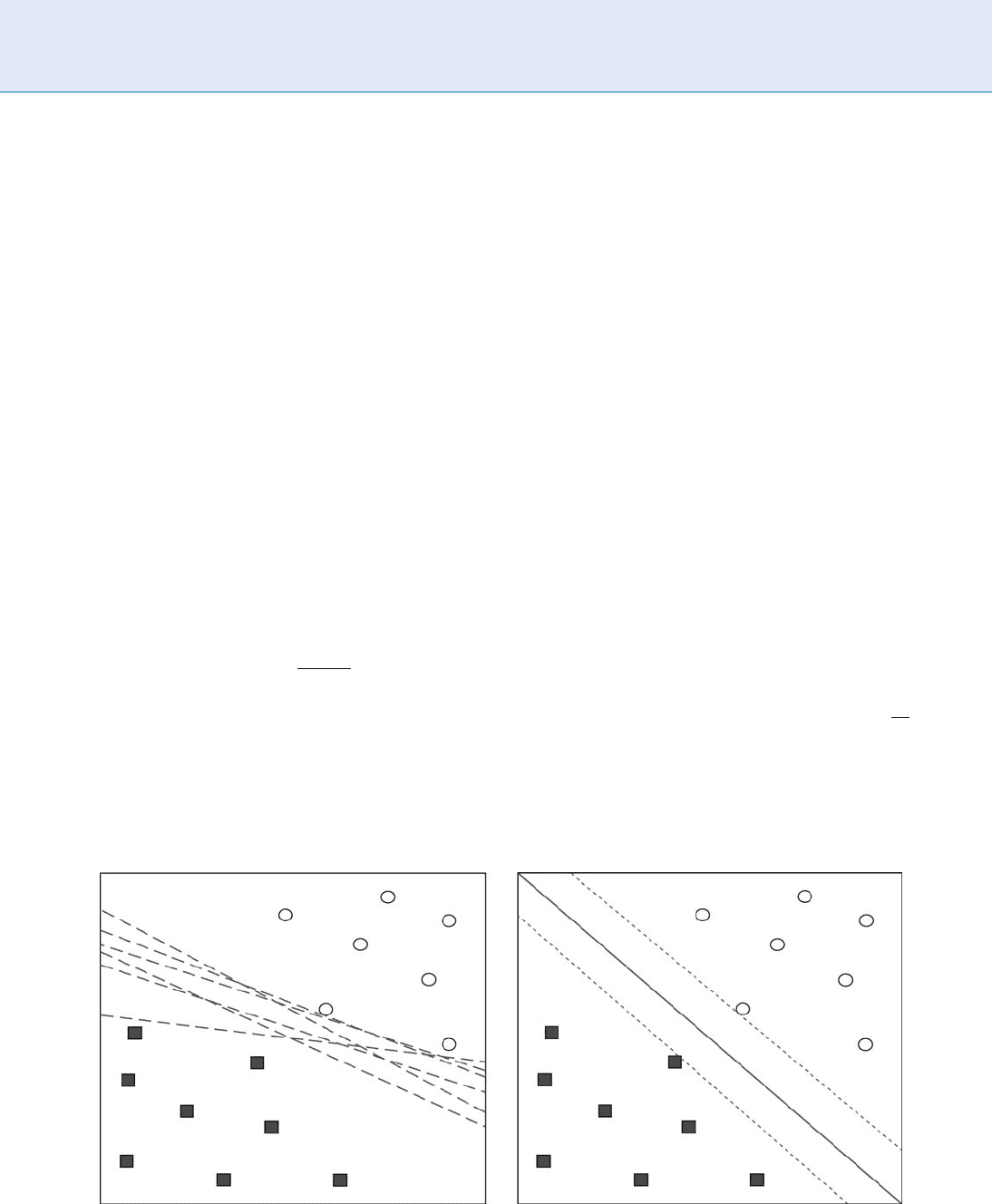
Considering a two-category classiﬁcation problem,

a linear classiﬁer separates the space, with a hyper-

plane, into two regions, each of which is also called a

class. Before the creation of SVMs, the popular algo-

rithm for determining the parameters of a linear clas-

siﬁer was a single-neuron perceptron. The perceptron

algorithm uses an updating rule to generate a separat-

ing surface for a two-class problem. The procedure

is guaranteed to converge when the

▶ training data

are linearly separable, however there exists an inﬁnite

number of hyperplanes that correctly classify these data

(see Fig. 1).

The idea behind the SVM is to select the hyper-

plane that provides the best generalization capa-

city. Then, the SVM algorithm attempts to ﬁnd the

maximum margin between the two data categories

and then determines the hyperplane that is in mid-

dle of the maximum margin. Thus, the points near-

est the decision boundary are located at the same

distance from the optimal hyperplane. In machine

learning theory, it is demonstrated that the margin

maximization principle provides the SVM with a

good generalization capacity, because it minimizes

the structural risk related to the complexity of the

SVM [1].

SVM Formulation

Let consider a dataset fðx

; y

Þ; ...; ðx

‘

; y

‘

Þg with

and y

2{1,1}. SVM training attempts to

ﬁnd the parameters w and b of the linear decision

function f(x) ¼ w.x þ b deﬁning the optimal hyper-

plane. The points near the decision boundary deﬁne

the margin. Considering two points x

, x

on opposite

sides of the margin with f(x

)¼1 and f(x

)¼1, the

margin equals ½f ðx

Þf ðx

Þ= w

¼ 2= w

. Thus,

maximizing the margin is equivalent to minimizing

||w||∕2or||w||

∕2. Then, to ﬁnd the optimal hyper-

plane, the SVM solves the following optimization

problem:

min

w;b

s:t y

þ bðÞ1 8i ¼ 1; ...;‘

ð1Þ

Support Vector Machine. Figure 1 Linear classifier: In this case, there exists an infinite number of solutions. Which is

the best?

1304

Support Vector Machine

The transformation of this optimization problem

into its corresponding dual problem gives the follow-

ing quadratic problem:

max

‘

i¼1



‘

i;j¼1



s:t

‘

i¼1

¼ 0; a  0 8i ¼ 1; ...;‘

ð2Þ

Where W

denotes the transpose of W.

The solution of the previous problem gives

the parameter w ¼

‘

i¼1

of the optimal

hyperplane. Thus, the decision function becomes

f ðxÞ¼

‘

i¼1

ðx

:xÞþb in dual space. Note that the

value of the bias b does not appear in the dual problem.

U sing the constraints of the primal problem, the bias

is given by b ¼1=2½max

y¼1

ðw:x

Þþmin

y¼1

ðw:x

Þ.

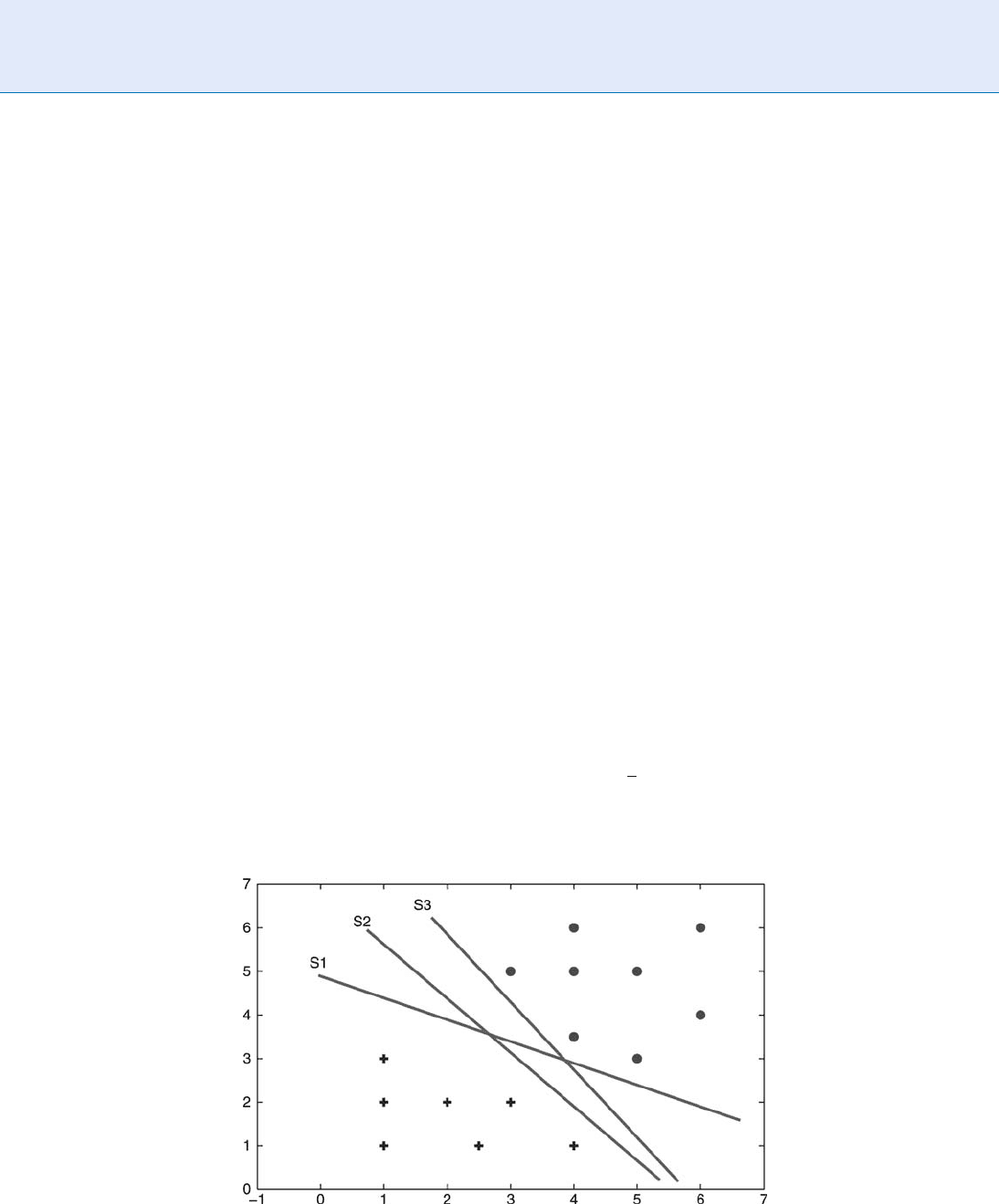
It is demonstrated with the Karush-Kuhn-Tucker

conditions that only the examples x

that satisfy

(w. x

þb)¼1 are the corresponding a

non-zero.

These examples are called support vectors (see Fig . 2).

SVM in Practice

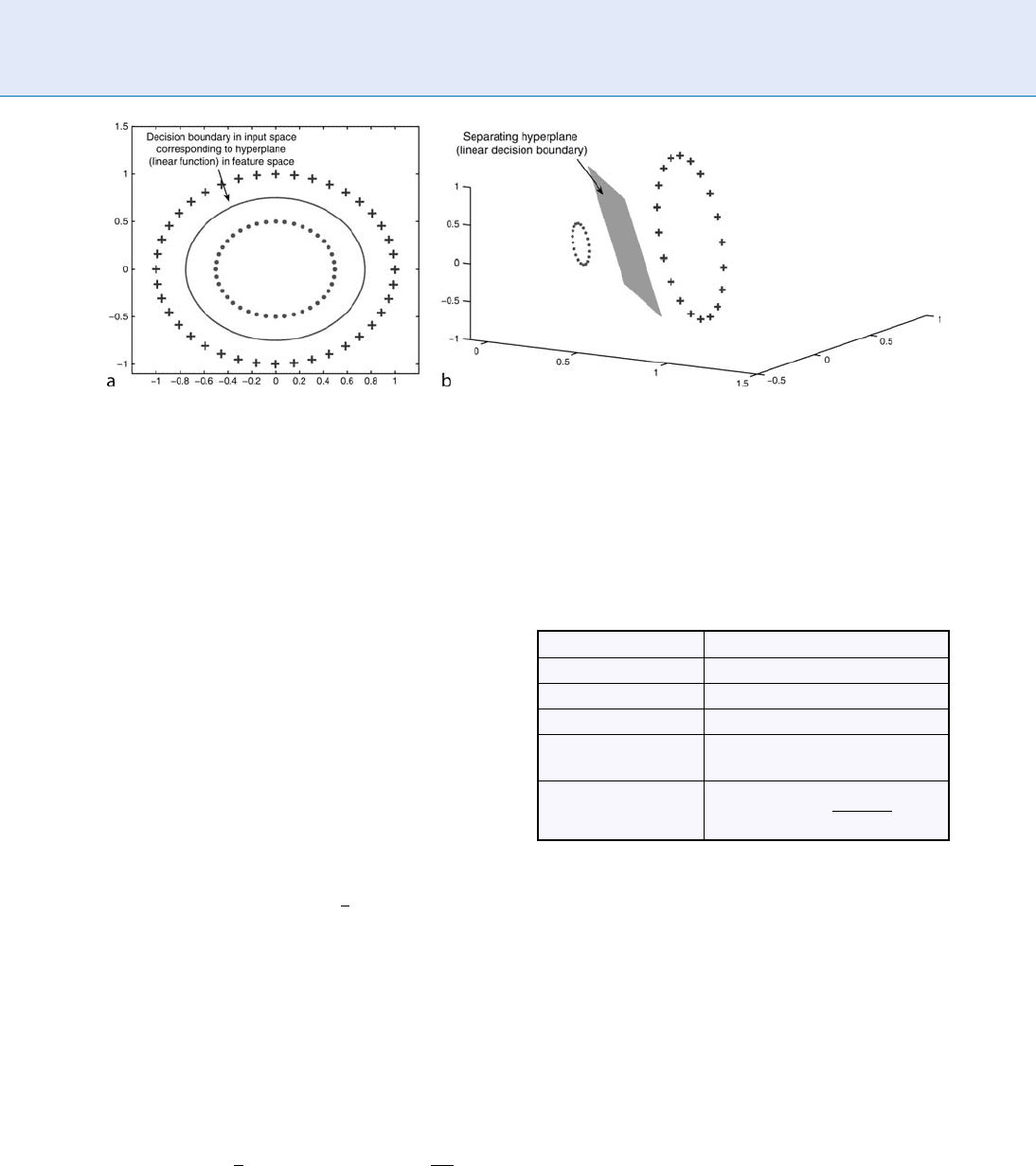
In real-world problems, the data are not linearly sepa-

rable, and so a more sophisticated SVM is used to solve

them. First, the slack variable is introduced in order to

relax the margin (this is called a soft margin optimiza-

tion). Second, the kernel trick is used to produce

nonlinear boundaries [2]. The idea behind kernels is

to map training data nonlinearly into a higher-dimen-

sional feature space via a mapping function F and to

construct a separating hyperplane whi ch maximizes

the margin (see Fig. 3). The construction of the line ar

decision surf ace in this feature space only requires the

evaluation of dot products f (x

).f(x

)¼k(x

), where

the application k : R

R

!Ris called the kernel

function [3, 4].

The decision function given by an SVM is:

yðxÞ¼sign½w

fðxÞþb; ð3Þ

where w and b are found by resolving the following

optimization problem that expresses the maximiza-

tion of the margin 2∕||w|| and the minimization of

training error:

min

w;b;x

w þ C

‘

i¼1

L1  SVMðÞor

min

w;b;x

w þ C

‘

i¼1

L2  SVMðÞ

ð4Þ

subject to : y

f x

ðÞ

þ b

½

 1  x

8i ¼ 1; ...;‘

ð5Þ

Support Vector Machine. Figure 2 SVM principle: illustration of the unique and optimal hyperplane in a

two-dimensional input space based on margin maximization.

Support Vector Machine

1305

 0 8i ¼ 1; ...;‘: ð6Þ

By applying the Lagrangian diffe rentiatio n theorem

to the corresponding dual problem, the followi ng

decision function is obtained:

yðxÞ¼sign½

i¼1

‘

kðx

; xÞþb; ð7Þ

with a solution of the dual problem.

The dual problem for the L1-SVM is the following

quadratic optimization problem:

maximize : W aðÞ¼

‘

i¼1



‘

i;j¼1

; x



ð8Þ

subject to :

‘

i¼1

¼0 and 0 a

C;i ¼1;...;‘: ð9Þ

Using the L2-SVM, the dual problem becomes :

maximize : W aðÞ¼

‘

i¼1



‘

i:j¼1

; x





ð10Þ

subject to :

‘

i¼1

¼ 0 and 0 a

; i ¼ 1; ...‘: ð11Þ

where d

¼ 1ifi ¼ j and 0 otherwise.

In practice, the L1-SVM is used most of the

time, and its popular implementation developed by

Joachims [ 5] is very fast and scales to large datasets.

This implementation, called SVMlig ht, is available

at svmlight.joachims.org.

SVM Model Selection

To achieve good SVM performance, optimum values

for the kernel parameters and for the hyperparameter C

much be chosen. The latter is a regularization parameter

controlling the trade-off between the training error min-

imization and the margin maximization. The kernel

parameters deﬁne the kernel function used to map data

into a higher-dimensional feature space (see Table 1).

Like kernel functions, there are the Gaussian kernel

k(x

)¼exp(||x

x

∕s

) with parameter s and

Support Vector Machine. Figure 3 Illustration of the kernel trick: The data are mapped into a higher-dimensional

feature space, where a separating hyperplane is constructed using the margin maximization principle. The hyperplane

is computed using the kernel function without the explicit expression of the mapping function. (a) Nonlinearly separable

data in the input space. (b) Data in the higher-dimensional feature space.

Support Vector Machine. Table 1 Common kernel used

with SVM

Gaussian (RBF) kðx; yÞ¼expðjjx  yjj

Polynomial kðx; yÞ¼ðax:y þ bÞ

Laplacian ðx; yÞ¼expðajjx  yjj þ bÞ

Multi-quadratic kðx; yÞ¼ðajjx yjjþ bÞ

1=2

Inverse multi-

quadratic

kðx; yÞ¼ðajjx  yjjþ bÞ

1=2

KMOD

kðx; yÞ¼a

exp



jjxyjj

þs



 1

1306

Support Vector Machine

the polynomial kernel k(x

, x

)¼(ax

þ b)

with

parameters a, b and d. The task of selecting the hyper-

parameters that yield the best performance of the ma-

chine is called model selection [6 , 7, 8, 9].

As an illustra tion, Fig. 4a shows the variation of

the error rate on a validation set versus the variation

of the Gaussian kernel with a ﬁxed value of C and

Fig. 4b shows the variation of the error rate on the

validation set versus the variation of the hyperpara-

meter C with a ﬁxed value of the RBF kernel parameter.

In each case, the binary problem described by the

‘‘Thyroid’’ data taken from the UCI benchmark is

resolved. Clearly, the best performance is achieved with

an optimum choice of the kernel parameter and of C.

With the SVM, as with other kernel classiﬁers, the

choice of kernel corresponds to choosing a function

space for learning. The kernel determines the function-

al form of all possible solutions. Thus, the choice of

kernel is very important in the construction of a good

machine. So, in order to obtain a good performance

from the SVM classiﬁer, one ﬁrst need to design

or choose a type of kernel, and then optimize the

SVM’s hyperparameters to improve the generalization

capacity of the classiﬁer. Figure 4c illustrates the inﬂu-

ence of the kernel choice, where the RBF and the

polynomial kernels are compared on datasets taken

from the challenge website on model selection and

prediction organized by Isabelle Guyon.

Resolution of Multiclass Problems with

the SVM

The SVM is formulated for the binary classiﬁcation

problem. However, there are some techniques used to

combine several binary SVMs in order to build a sys-

tem for the multiclass problem (e.g., a 10-class digit

recognition problem). Two popular methods are pre-

sented here:

OneVersustheRest: The idea of one versus the rest

is to construct as many SVMs as there are classes,

where each SVM is traine d to separate one class from

the rest. Thus, for a c-class problem, c SVMs are built

and combined to perform multiclass classiﬁcation

according to the maximal output. The ith SVM is

trained with all the examples in the ith class with

positive labels, and all the other examples with negative

examples. This is also known as the One-Against-All

method.

Pairwise(orOneAgainstOne): The idea of pair-

wise is to construct c(c1)2 SVMs for a c-class prob-

lem, each SVM being trained for every possible pair of

classes. A common way to make a decision with the

pairw ise method is by voting. A rule for discriminating

between every pair of classes is constructed, and the

class with the largest vote is selected.

SVM Variants

The least squares SVM (LS-SVM) is a variant of

the standard SVM, and constitutes the response

to the following question: How much can the SVM

formulation be simpliﬁed without losing any of its

advantages? Suykens and Vandewalle [10] proposed

the LS-SVM where the training algorithm solves a

convex problem like the SVM. In addition, the training

algorithm of the LS-SVM is simpliﬁed, since a linear

problem is resolved instead of a quadratic problem

in the SVM case.

Support Vector Machine. Figure 4 (a) and (b) show the impact of SVM hyperparameters on classiﬁer generalization,

while (c) illustrates the inﬂuence of the choice of kernel function.

Support Vector Machine

1307

The Transductive SVM (TSVM) is an interesting

version of the SVM, which uses transductive inference.

In this case, the TSVM attempts to ﬁnd the hyperplane

and the labels of the test data that maximize the

margin with minimum error. Thus, the label of the

test data is obtained in one step. Vapnik [1] proposed

this formulation to reinforce the classiﬁer on the test

set by adding the minimization of the error on the

test set during the training process. This formula-

tion has been used elsewhere recently for training

semi-supervised SVMs.

Applications

The SVM is a powerful classiﬁer which has been used

successfully in many pattern recognition problems,

and it has also been shown to perform well in

biometrics recognition applications. For example, in

[11], an iris recognition system for human identiﬁca-

tion has been proposed, in which the extracted iris

features are fed into an SVM for classiﬁcation. The

experimental results show that the performance of

the SVM as a classiﬁer is far better than the perfor-

mance of a classiﬁer based on the artiﬁcial neural

network. In another example, Yao et al. [12], in a

ﬁngerprint classiﬁcation application, used recursive

neural networks to extract a set of distributed features

of the ﬁngerprint which can be integrated into the

SVM. Many other SVM applications, like handwriting

recognition [8, 13], can be found at www.clopinet.

com/isabelle/Projects/SVM/applist.html.

Related Entries

▶ Classiﬁer

▶ Generalization

▶ Structural Risk

▶ Training

References

1. Vapnik, V.N.: Statistical learning theory. Wiley, New York (1998)

2. Boser, B.M.E., Guyon, I., Vapnik, V.: A training algorithm for

optimal margin classiﬁers. In: Proceedings of Fifth Annual

Workshop on Computational Learing Theory, pp. 144–152

(1992)

3. Scholkopf, B., Smola, A.J.: Learning with Kernels. MIT Press,

Cambridge, MA (2002)

4. Cristianini, N., Shawe-Taylor, J.: An Introduction to Support

Vector Machines. Cambridge Universit y Press (2000)

5. Joachims, T.: Making large-scale support vector machine

learning practical. In: Scholkopf, Burges, Smola (eds.) Advances

in Kernel Methods: Support Vector Machines. MIT Press,

Cambridge, MA (1998)

6. Chapelle, O., Vapnik, V.: Model selection for support vector

machines. Advances in Neural Information Processing Systems

(1999)

7. Ayat, N.E., Cheriet, M., Suen, C.Y.: Automatic Model Selection

for the Optimization of the SVM kernels. Pattern Recognit.

38(10), 1733–1745 (2005)

8. Adankon, M.M., Cheriet, M.: Optimizing Resources in Model

Selection for Support Vector Machines. Pattern Recognit. 40(3),

953–963 (2007)

9. Adankon, M.M., Cheriet, M.: New formulation of svm

for model selection. In: IEEE International Joint Conference

in Neural Networks 2006, pp. 3566–3573. Vancouver, BC

(2006)

10. Suykens, J.A.K., Van Gestel, T., De Brabanter, J., De Moor, B.,

Vandewalle, J.: Least Squares Support Vector Machines. World

Scientiﬁc, Singapore (2002)

11. Roy, K., Bhattacharya, P.: Iris recognition using support vector

machine. In: APR International Conference on Biometric

Authentication (ICBA), Hong Kong, January 2006. Springer

Lecture Note Series in Computer Science (LNCS), pp. (3882)

486–492 (2006)

12. Yao, Y., Marcialis, G.L., Pontil, M., Frasconi, P., Rolib, F.:

Combining ﬂat and structured representations for ﬁngerprint

classiﬁcation with recursive neural networks and support vector

machines. Pattern Recognit. 36(2), 397–406 (2003)

13. Matic, N., Guyon, I., Denker, J., Vapnik, V.: Writer adaptation

for on-line handwritten character recognition. In: IEEE

Second International Conference on Pattern Recognition and

Document Analysis, pp. 187–191. Tsukuba, Japan (1993)

Surface Curvature

Measurements of the curvature of a surface are com-

monly used in 3D biometrics. The normal curvature on

a point p on the surface is deﬁned as the curvature of

the curve that is formed by the intersection of the

surface w ith the plane containing the normal vector

and one of the tangent vectors at p. Thus the normal

curvature is a function of the tangent vector direction.

The minimum and maximum values of this function

are the principal curvatures k1 and k2 of the surface

1308

Surface Curvature

at p. Other measures of surface curvature are the

Gaussian curvature deﬁned as the product of principal

curvatures, the mean curvature deﬁned as the average

of principal curvatures and the shape index given by

SI ¼

þ k

 k

Computation of surface curvature on discrete surfaces

such as those captured with 3D scanners is usually

accomplished by locally ﬁtting low order surface

patches (e.g. biquadratic surfaces, splines) over each

point. Then the above curvature features may be com-

puted analytically.

▶ Finger Geometry, 3D

Surface Matching

3D biometrics work by computing the similarity be-

tween 3D surfaces of objects belonging to the same

class. The majority of the techniques used measure

the similarit y among homologous salient geometric

features on the surfaces (e.g. based on curvature).

The localization of these features is usually based on

prior knowledge of the surface class (e.g. face, hand)

and thus, specialized feature detectors may be used.

The geometric attributes extracted are selected so that

they are invariant to transformations such as rotation,

translation and scaling. In the case that knowledge-

based feature detection is difﬁcult, a correspondence

among the surfaces may be established by randomly

selecting points on the two surfaces and then trying to

ﬁnd pairs of points with similar geometric attributes.

Several such techniques have been developed for rigid

surface matching (e.g. Spin Images) which may be

extended for matc hing non-rigid or articulated sur-

faces. Another techn ique for establishing correspon-

dences is ﬁtting a param eterized deformable model to

the points of each surface. Since the ﬁtted models are

deformations of the same surface, correspondence is

automatically determined. Creation of such deform-

able models requires however a large number of anno-

tated training data.

▶ Finger Geometry, 3D

Surveillance

RAMA CHELLAPPA,ASWIN C. SANKARANARAYANAN

University of Maryland, College Park, MD, USA

Synonyms

Monitoring; Surveillance

Definition

Surveillance refers to monitoring of a scene along

with analysis of behavior of the people and vehicles

for the purpose of maintaining security or keeping a

watch over an area. Typically, traditional surveillance

involves monitoring of a scene using one or more

close circuit television (CCTV) cameras with person-

nel watching and making decisions based on video

feeds obtained from the

▶ cameras. There is a grow-

ing need towards building systems that are com-

pletely automated or operate with minimal human

supervision.

Biometric acquisition and processing is by far the

most important component of any automated surveil-

lance system. There are many challenges and variates that

show up in acquisition of biometrics for robust veriﬁca-

tion. Further, in surveillance, behavioral biometrics is

also of potential use in many scenarios. Using the pat-

terns observed in a scene (such as faces, speech, behav-

ior), the system decides on a set of actions to perform.

These actions could involve access control (allowing/

denying access to facilities), alerting the presence of

intruders/abandoned luggage and a host of other secu-

rity related tasks.

Introduction

Surveillance refers to monitoring a scene using sensors

for the purposes of enhanced security. Surveillance

systems are becoming ubiquitous , especially in urban

areas with growing deployment of cameras and CCTV

for providing security in public areas such as banks,

shopping malls, etc. It is estimated that UK alone

has more than four million CCTV cameras. Surveil-

lance technologies are also becoming common for

Surveillance

1309