Лекции по гидрогазодинамике
Подождите немного. Документ загружается.

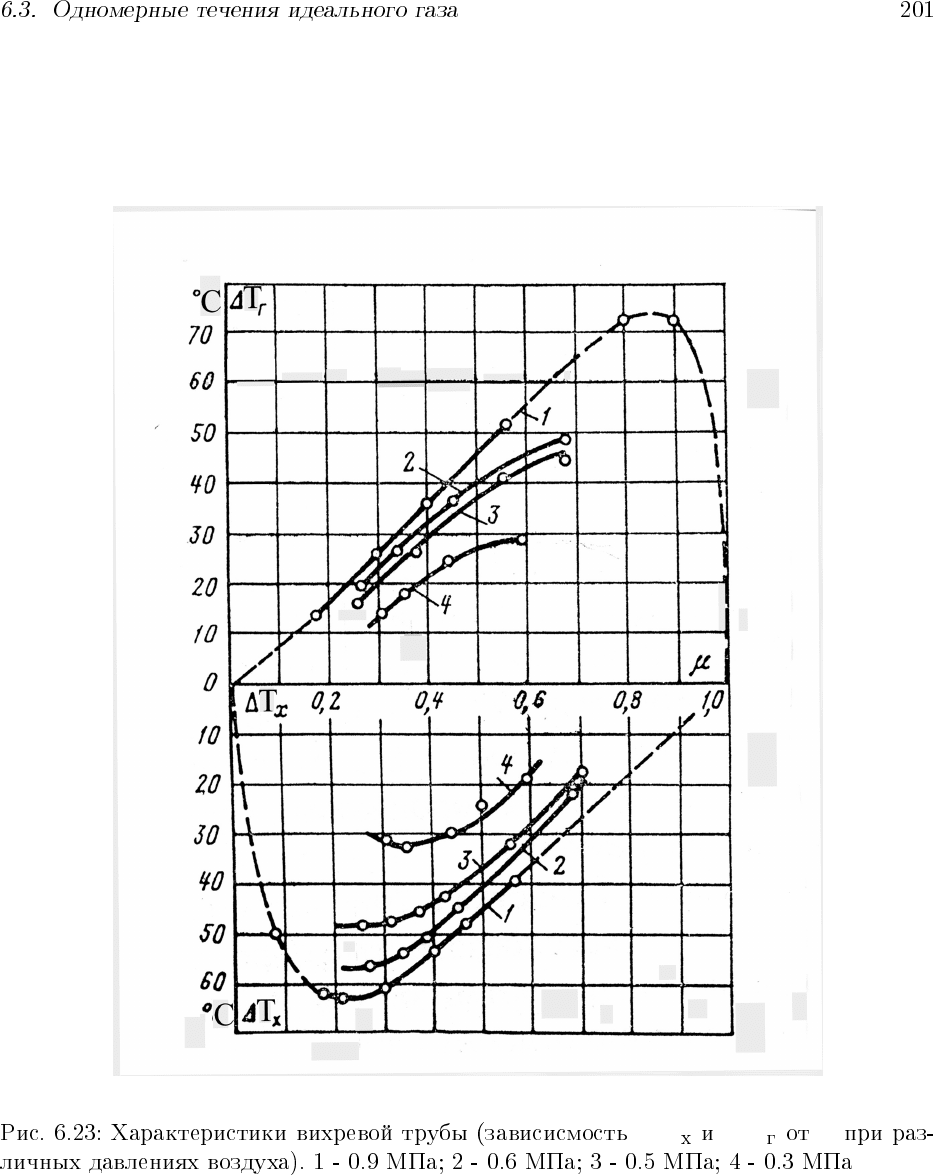
∆ T ∆ T µ

~n
-
~v
1
*
~v
2
~n
ρ
1
, T
1
, p
1
ρ
2
, T
2
, p
2

ρ
1
(~v
1
~n) = ρ
2
(~v
2
~n),
ρ
1
~v
1
(~v
1
~n) + p
1
~n = ρ
2
~v
2
(~v
2
~n) + p
2
~n,
ρ
1
(~v
1
~n)
v
2
1
2
+ h
1
= ρ
2
(~v
2
~n)
v
2
2
2
+ h
2
.
x, y
(~v
j
~n) = v
jn
, j = 1, 2
ρ
1
v
1n
v
1x
= ρ
2
v
2n
v
2x
,
ρ
1
v
1n
v
1y
= ρ
2
v
2n
v
2y
.
ρ
1
v
1n
= ρ
2
v
2n
= 0 ρ
1
, ρ
2
v
1n
= v
2n
= 0
p
1
= p
2
v
1n
v
2n
ρ
1
v
1n
= ρ
2
v
2n
v
1x
= v
2x
, v
1y
= v
2y

v
2
= v
2
n
+ v
2
x
+ v
2
y
.
ρ
1
v
1n
= ρ
2
v
2n
,
ρ
1
v
2
1n
+ p
1
= ρ
2
v
2
2n
+ p
2
,
v
1x
= v
2x
,
v
1y
= v
2y
,
v
2
1n
2
+ h
1
=
v
2
2n
2
+ h
2
.
v
1n
= v
1
; v
2n
= v
2
v
1x
= v
2x
= 0; v
1y
= v
2y
= 0.
ρ
1
v
1
= ρ
2
v
2
,
ρ
1
v
2
1
+ p
1
= ρ
2
v
2
2
+ p
2
,
v
2
1
2
+ h
1
=
v
2
2
2
+ h
2
.

v
1
v
2
(ρ
2
− ρ
1
) = p
2
− p
1
,
v
1
v
2
=
p
2
− p
1
ρ
2
− ρ
1
.
h = c
p
T =
k R T
k − 1
k = c
p
/c
v
v
2
j
2
+ c
p
T
j
= h
0
= c
p
T
0
, j = 1, 2.
p
j
= ρ
j
R T
0
−
(k − 1)
2 k
v
2
j
, j = 1, 2.
p
2
− p
1
j = 2
j = 1
p
2
− p
1
= (ρ
2
− ρ
1
)
2 k R T
0
k + 1
,
v
1
v
2
=
p
2
− p
1
ρ
2
− ρ
1
=
2 k R T
0
k + 1
= v
2
.
v
1
v
2
= v
2
.
v
1
> v
v
2
< v

p
2
+ p
1
j = 2 j = 1
p
2
+ p
1
= (ρ
2
+ ρ
1
) R T
0
−
(k − 1)
2 k
(ρ
2
v
2
2
+ ρ
1
v
2
1
).
p
2
− p
1
ρ
2
− ρ
1
=
1
k
p
2
+ p
1
ρ
2
+ ρ
1
,
ρ
2
ρ
1
=
k + 1
k − 1
+
p
1
p
2
k + 1
k − 1
p
1
p
2
+ 1
.
p V
k
=
p
ρ
k
= const;
ρ
2
ρ
1
=
p
2
p
1
!
1/k
.
p
2
p
1
→ ∞
ρ
2
ρ
1
→ ∞;

p
2
p
1
→ ∞
ρ
2
ρ
1
→
k + 1
k − 1
.
dS =
dq
T
=
1
T
(dh − V dp) =
c
p
dT
T
−
dp
ρ T
=
=
k R
k − 1
"
dp
p
−
dρ
ρ
#
− R
dp
p
=
R
k − 1
"
dp
p
− k
dρ
ρ
#
.
∆S =
(2)
Z
(1)
dS =
R
k − 1
ln
p
2
p
1
ρ
1
ρ
2
!
k
=
R
k − 1
ln(A).
p
2
p
1
=
ρ
2
ρ
1
!
k
, ∆S = ln(A = 1) = 0.
p
2
p
1
>
ρ
2
ρ
1
!
k
, ∆S = ln(A > 1) > 0.

∂
2
p
∂V
2
S
> 0
V S
∂
2
p
∂V
2
S
< 0.

v
n
= v
ρ
1
v
1
= ρ
2
v
2
,
ρ
1
v
2
1
+ p
1
= ρ
2
v
2
2
+ p
2
.
q
h
1
+
v
2
1
2
+ q = h
2
+
v
2
2
2
.
p
1
= ρ
1
R
1
T
1
, p
2
= ρ
2
R
2
T
2
.
k
1
6= k
2
T
(1)
0
6= T
(2)
0
v
(j)
=
v
u
u
u
t
2 k
j
R
j
T
(j)
0
k
j
+ 1
, j = 1, 2.
h
j
= k
j
R
j
/(k
j
− 1)
λ
j
= v
j
/v
(j)
λ
2
2
−
K
1 + λ
2
1
λ
1
√
1 + q
λ
2
+ 1 = 0,
K =
k
2
k
1
v
u
u
u
t
k
2
1
− 1
k
2
2
− 1
, q =
q
h
(1)
0
.

λ
2
=
1
2
K
1 + λ
2
1
λ
1
√
1 + q
±
v
u
u
u
t
K
2
(1 + λ
2
1
)
2
4 λ
2
1
(1 + q)
− 1.
k
1
= k
2
= k; K = 1
λ
2
=
1
2
1 + λ
2
1
λ
1
√
1 + q
±
v
u
u
u
t
(1 + λ
2
1
)
2
4 λ
2
1
(1 + q)
− 1.
λ
1
> 1 λ
1
< 1
√
1 + q
λ
2
< 1 λ
2
> 1
λ
1
< 1 λ
2
> 1
λ
1
> 1 λ
2
> 1
λ
1
> 1 λ
2
< 1
p
2
> p
1
λ
1
< 1 λ
2
< 1
p
2
< p
1
