Лекции по гидрогазодинамике
Подождите немного. Документ загружается.


h +
v
2
2
= const.
h = C
p
·T
C
p
T
0
= T +
v
2
2 C
p
.
C
p
C
V
k
R
C
p
C
V
= k − ,

C
p
− C
V
= R − .
C
p
C
V
C
p
=
k R
k − 1
,
T
0
= T +
k − 1
2
v
2
k R
,
T
0
T
= 1 +
k − 1
2
M
2
,
M = v/c
k = 1.4; R = 287 /[ · K]
T
0
= T +
v
2
2000
.
−56
C v = 2200 / ≈ 611 /c T
0
= 131
C
∼ 8 /c
30000 K

K
p
0
p
=
T
0
T
!
k/(k−1)
,
ρ
0
ρ
=
T
0
T
!
1/(k−1)
.
[∆ ρ/ρ]
max
= δ ∆ ρ = ρ
0
−ρ
ρ
0
ρ
− 1 =
∆ ρ
ρ
= δ =
1 +
k − 1
2
M
2
!
1
k − 1
− 1.
M = v/c
v
max
δ
v
max
≈ c
√
2 δ
δ ∼ 10
−2
δ
v 6
v
max
c
2
k − 1
+
v
2
2
= h
0
= const.

v = c =
v
v
2
k − 1
+
v
2
2
= h
0
=
k R T
0
k − 1
,
v =
v
u
u
t
2 k R T
0
k + 1
.
M =
v
c
= 1
M = 1
T
T
0
=
2
k + 1
;
p
p
0
=
2
k + 1
!
k/(k−1)
;
ρ
ρ
0
=
2
k + 1
!
1/(k−1)
.
M = v/c
λ = v/v
λ

τ =
T
T
0
=
1 +
k − 1
2
M
2
!
−1
= 1 −
k − 1
k + 1
λ
2
;
ε =
ρ
ρ
0
=
1 +
k − 1
2
M
2
!
−
1
k − 1
=
=
1 −
k − 1
k + 1
λ
2
!
1
k − 1
;
π =
p
p
0
=
1 +
k − 1
2
M
2
!
−
k
k − 1
=
1 −
k − 1
k + 1
λ
2
!
k
k − 1
.
τ, ε, π
k
M = v/c λ = v/v
∗
λ = M = 1
q = f(k, M) = φ(k, λ)
q =
ρ v
ρ
∗
v
∗
=
S
∗
S
.
q
q =
S
∗
S
=
ε λ
ε
∗
=
k + 1
k
!
k/k−1
λ
1 −
k − 1
k + 1
λ
2
!
1/k−1
.
q = 1

dx
dS
dG dL
dQ
dL
G = ρ v S
dG
G
=
dρ
ρ
+
dv
v
+
dS
S
.
d
v
2
2
+
dp
ρ
+ dL + dψ + dL +
dG
G
v v = 0.

dQ = dh + d
v
2
2
+ dL .
p = ρ R T
dp
p
=
dρ
ρ
+
dT
T
.
c =
√
k R T ; M = v/c
(M
2
− 1)
dv
v
=
dS
S
−
dG
G
−
1
c
2
dL −
k − 1
c
2
dQ −
k
c
2
dL .
M = 1
dv > 0 M < 1
dS < 0 dG > 0
dL > 0 dL dQ > 0
dS > 0; dG < 0 dL < 0; dL ; dQ < 0
dL > 0
dL = 0
dG = 0
dL = 0; dQ = 0
(M
2
− 1)
dv
v
=
dS
S
.
dv > 0
M < 1 dS < 0
M = 1
dS > 0
ρ
G = ρ v S = ρ ∼
S

ρ ρ ∼ 1/v
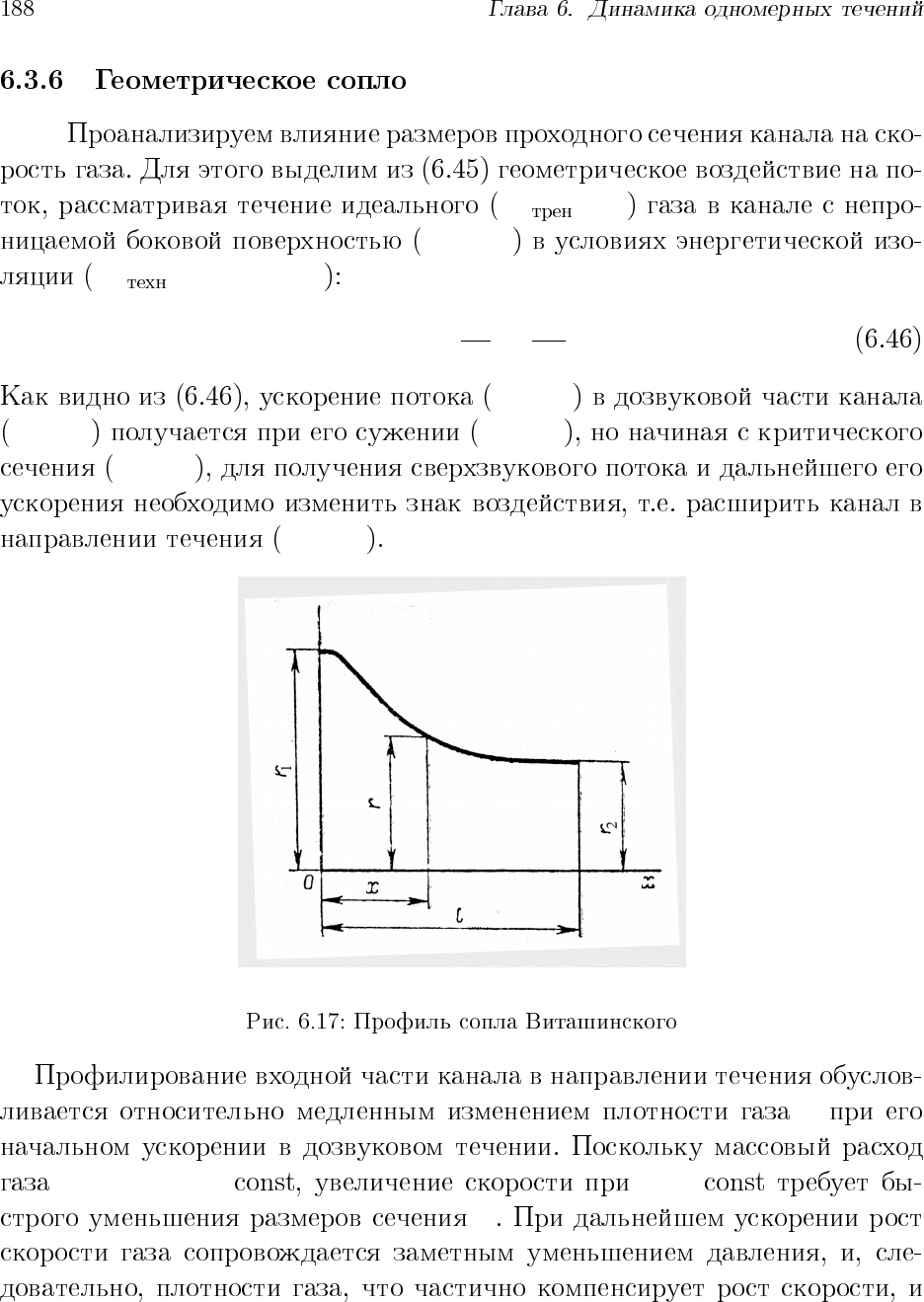
r = r(x)
r =
r
2
v
u
u
u
t
1 −
1 −
r
2
r
1
!
2
1 − x
2
/l
2
2
(1 + 3 x
2
/l
2
)
3
,
r, x
r
1
, r
2
l 4 r
1
v/v = 0.9 − 0.95
v =
q
2 (h
0
− h) =
v
u
u
t
2 C
p
T
0
1 −
T
T
0
!
v = 0
p
p/p
0
= ε
T
T
0
=
p
p
0
!
(k−1)/k
= ε
(k−1)/k
,
ρ
ρ
0
=
p
p
0
!
1/k
= ε
1/k
.
G = ρ v S
ρ = ρ
0
(ρ/ρ
0
)
G = ρ
0
S ε
1/k
r
2 C
p
T
0
1 − ε
(k−1)/k
= B f(ε).
B = ρ
0
S
q
2 C
p
T
0
=
f(ε) = ε
1/k
q
(1 − ε
(k−1)/k
).
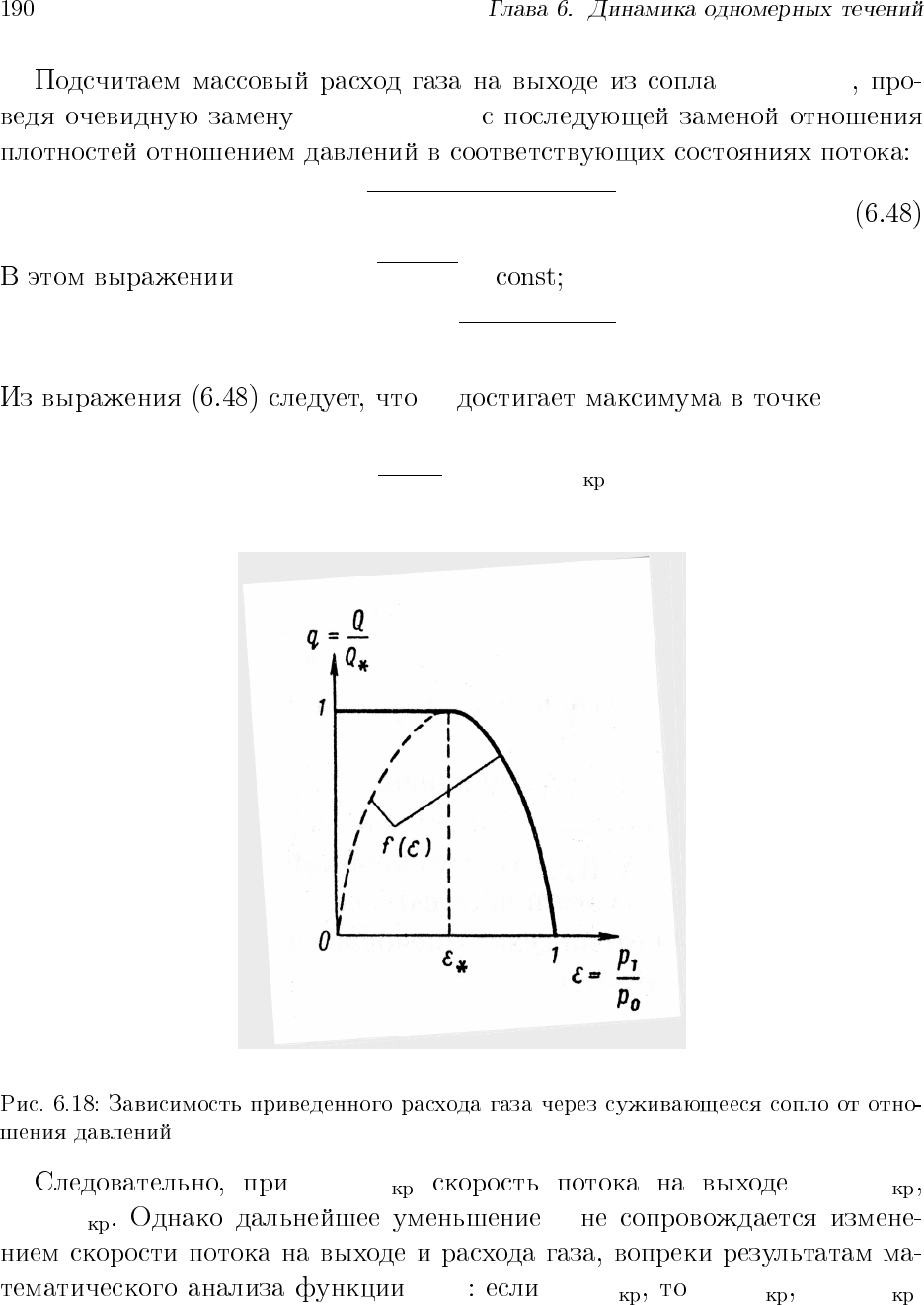
G
ε =
2
k + 1
!
k/(k−1)
= ε .
ε > ε v 6 v
G 6 G ε
f(ε) ε < ε v = v G = G .
