Лекции - Физика плазмы
Подождите немного. Документ загружается.

1
ТЕМА 1
ОСНОВНЫЕ ПОНЯТИЯ О ПЛАЗМЕ
ЛЕКЦИЯ 1
ПЛАЗМА КАК СОСТОЯНИЕ ВЕЩЕСТВА
1. Квазинейтральность плазмы
Живя на Земле, мы привыкли к телам в твёрдом, жидком или
газообразном состояниях. Однако из астрофизических данных следует, что
подавляющая часть вещества Вселенной находится в четвёртом состоянии
вещества — плазменном.
Плазмой называется ионизированный газ с достаточно высокой
концентрацией
заряженных частиц, обладающий свойством
квазинейтральности.
Квазинейтральная плазма — это плазма, электрически нейтральная в
среднем в достаточно большом объёме или за достаточно большой
промежуток времени. Величины объёмов и промежутков времени, в которых
проявляется квазинейтральность, определяются пространственным и
временным масштабами разделения зарядов. Квазинейтральность плазмы
означает, что в достаточно большом объёме плазмы количество
положительных
и отрицательных частиц практически одинаково.
Положительно заряженные частицы — это всегда ионы, а отрицательно
заряженные — обычно электроны. В результате «прилипания» электронов к
нейтральным атомам в плазме могут возникать и отрицательно заряженные
ионы, но они встречаются редко и имеют второстепенное значение.
Отношение числа ионизированных атомов
к их полному числу
в том же объёме называется степенью ионизации плазмы
(·
):
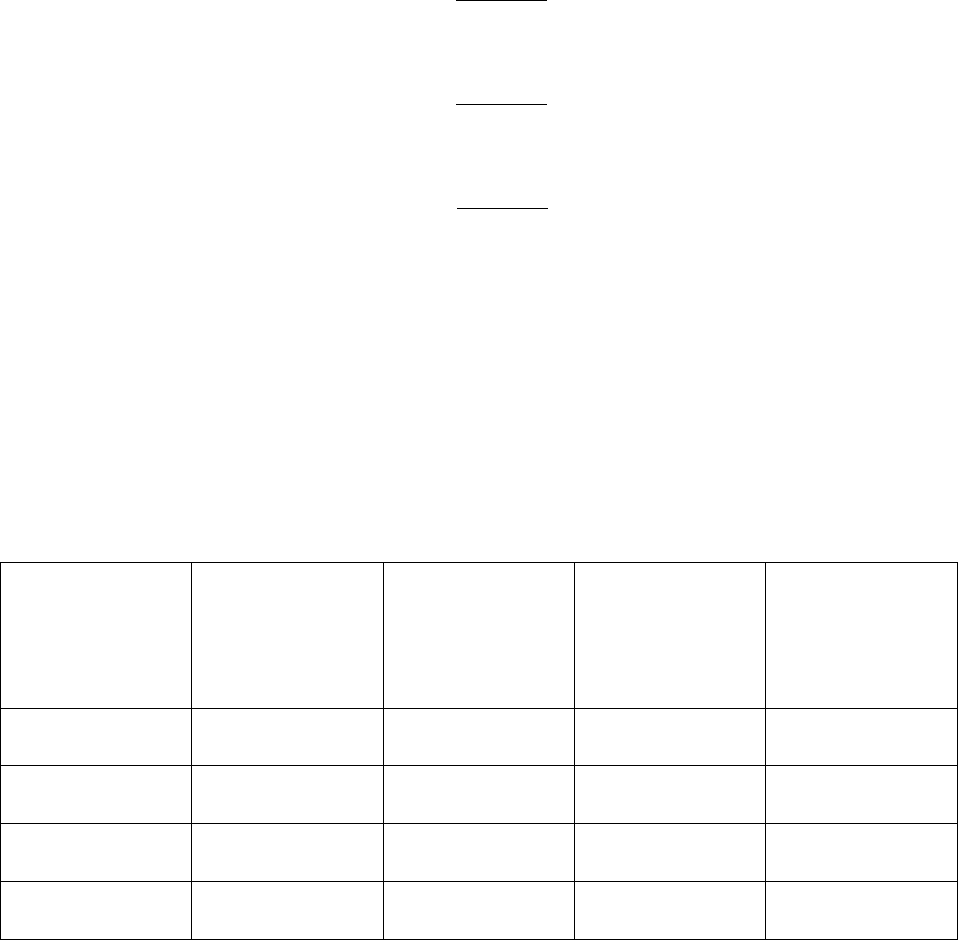
2
ai
i
nn
n
+
=α
;
ai
i
nn
nz
+
⋅
=α
;
или
ai
e
nn
n
+
=α
.
В большинстве реальных случаев плазма представляет собой смесь
нейтральных и заряженных частиц, при этом степень ионизации α мала.
Такую систему называют слабоионизированной плазмой. Отметим, что
плазмой может быть состояние, в котором
α
~10
-3
.
Примеры слабоионизированной плазмы
Тип плазмы
Фотосфера
Солнца
Е-слой
дневной
атмосферы
Гелий-
неоновый
лазер
Аргоновый
лазер
e
n
, см
-3
10
14
10
5
3·10
11
10
13
a
n
, см
-3
10
17
10
13
2·10
16
10
14
e
T
, К
6000 250 3·10
4
10
5
a
T
, К
6000 250 400 10
3
Здесь
aie
n,n,n
– концентрации электронов, ионов, нейтральных частиц;
ae
T,T
– температуры электронов и нейтральных частиц.
2. Разделение зарядов
Рассмотрим масштаб разделения зарядов во времени. Пусть в плазме в
результате разделения зарядов возник объёмный заряд с плотностью
e
ρ
. По
закону сохранения заряда:

3
jdiv
t
e
r
−=
∂
ρ
∂
, (1)
где
j
r
– плотность тока. Если ток переносится только электронами, то:
vnej
e
r
r
⋅⋅−=
, (2)
где
v
r
– скорость электронов, переносящих ток.
Уравнение движения электрона:
Ee
dt
vd
m
r
r
⋅−=⋅
. (3)
Из (1)-(3) имеем:
)vne(div
t
e
e
r
⋅⋅=
∂
ρ
∂
.
Продифференцируем по времени, получим:
)
dt
vd
(divne
t
e
2
e
2
r
⋅⋅=
∂
ρ
∂
,
Ediv
m
ne
t
e
2
2
e
2
r
⋅
⋅
−=
∂
ρ
∂
. (4)
При этом, имея в виду линейные колебания и не делая различия
между частотой и полной производной по времени, мы отбросили все
квадратичные члены, а не вынесли за знаки дифференциалов.
По уравнению Максвелла:
e
0
1
Ediv ρ⋅
ε
=
r
,
тогда:
e
0
e
2
2
e
2
m
ne
t
ρ⋅
ε⋅
⋅
−=
∂
ρ
∂
. (5)
Полученное уравнение описывает гармонические колебания с
частотой:
0
e
2
0
m
ne
ε⋅
⋅
=ω
. (6)
4
Частота
0
ω
называется плазменной частотой.
Таким образом, в случае разделения в плазме зарядов возникающие
электростатические силы вызывают так называемые электростатические, или
ленгмюровские колебания. Электростатические колебания были обнаружены
Ленгмюром и Томпсом (1929 г.) в газовом разряде.
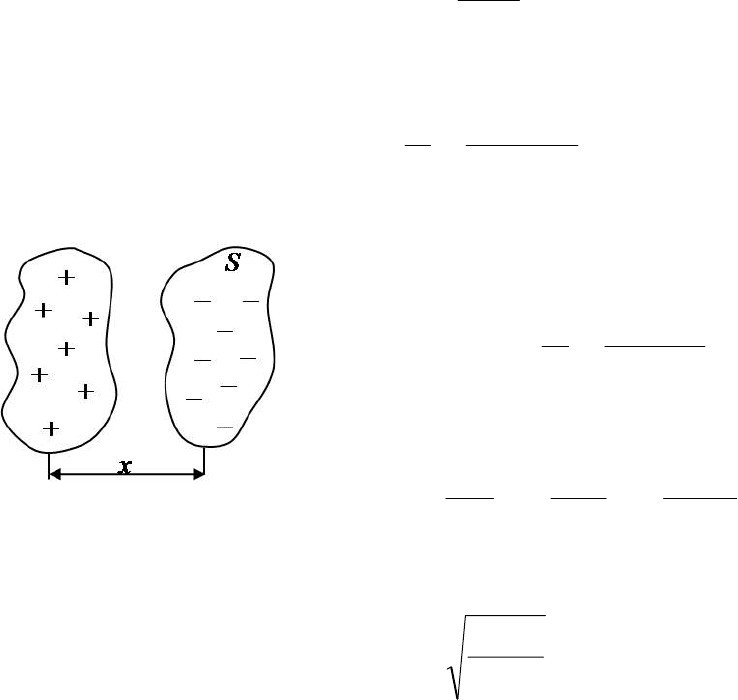
Возникновение плазменных колебаний объясняется следующим
образом: локальное нарушение квазинейтральности происходит в результате
смещения электронов из слоя толщиной
x
на одну из «ограничивающих»
этот слой плоскостей, при этом образуется как бы «конденсатор». Заряд
этого конденсатора равен:
xenSQ
e
⋅
⋅
⋅
=
,
ёмкость:
x
S
C
0
⋅
ε
=
,
а разность потенциалов:
0
2
e
xen
C
Q
U
ε
⋅
⋅
== .
Величина однородного электрического поля между
пластинами конденсатора:
.
xen
x
U
E
0
e
ε
⋅
⋅
==
Это поле сообщает каждому электрону ускорение
.x
m
en
m
Ee
dt
xd
0
e
2
2
⋅
ε⋅
⋅
−=
⋅
−=
Полученное уравнение описывает колебания с частотой:
.
m
ne
0
e
2
0
ε⋅
⋅
=ω
Отметим, что у плазмы много различных типов колебаний, особенно,
если она помещена в магнитное поле. Но плазменными колебаниями принято
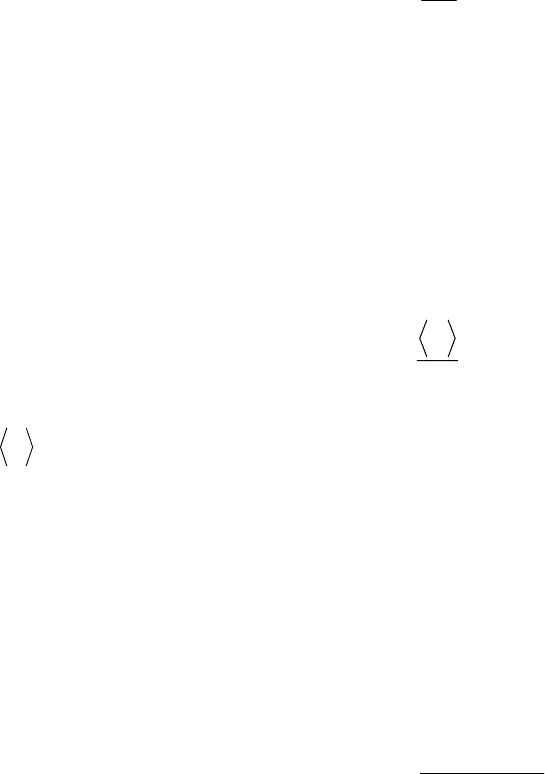
5
называть не всякие колебания плазмы, а именно электростатические
колебания с частотой
0
ω
. Таким образом, «плазменные колебания» и
«колебания плазмы» – не одно и то же. Термин «колебания плазмы» имеет
более широкий смысл. Плазменные колебания не имеют волнового характера
– нарушения электронейтральности не распространяются по плазме.
Временной масштаб разделения зарядов есть величина того же
порядка, что и период плазменных колебаний:
0
t
~
0
1
ω
. (7)
Разделение зарядов может быть существенным только за периоды времени,
малые по сравнению с этим масштабом.
За пространственный масштаб разделения зарядов
d
можно принять
расстояние, которое частица при своём тепловом движении проходит за
время
0
t
:
d
~
0
v
ω
, (8)
где
v
– средняя скорость теплового движения частиц.
В масштабах, больших по сравнению с
d
, соблюдается
квазинейтральность.
Пространственный масштаб разделения зарядов можно рассмотреть и
с энергетической точки зрения. В электрическом поле чтобы преодолеть
разность потенциалов
U
электрон должен обладать энергией
ε
0
22
e
xen
Ue
ε
⋅
⋅
=⋅=
. (9)
Расстояние, на котором может быть заметным разделение зарядов
вследствие теплового движения, определяется тем условием, что энергия (9)
должна быть одного порядка с энергией теплового движения
Tk ⋅
. Тогда

6
расстояние
d
, на котором возможно заметное разделение зарядов, находится
из условия:
Tk
den
0
22
e
⋅=
ε
⋅
⋅
,
откуда:
2
e
0
en
Tk
d
⋅
⋅⋅ε
=
. (10)
Разделив числитель и знаменатель под корнем на
m
и подставив
вместо средней скорости теплового движения близкую к ней величину
mTkv ⋅≈
, можно убедиться, что выражение (10) тождественно формуле
(8).
Для плазмы, имеющей определённую температуру, выражение (8)
следует рассматривать как приближение, а (10) – как точное. Но поскольку
плазма часто не находится в состоянии термодинамического равновесия, то
понятие температуры теряет для неё строгий смысл. В этом случае
пространственный масштаб
d
разделения зарядов для частиц каждого рода
определяется формулой (8).
Пространственный масштаб
d
разделения зарядов называют также
поляризационной длиной, так как это наибольшая длина, на которой
вследствие теплового движения самопроизвольно возникают разности
потенциалов, то есть происходит поляризация плазмы. В частности, у
границы плазмы возникает слой, в котором квазинейтральность нарушается,
причём толщина этого граничного слоя порядка пространственного масштаба
разделения зарядов.
Если разделение зарядов происходит
в результате смещения
электронов, то найденную частоту
0
ω
называют электронной плазменной
частотой, а соответствующий пространственный масштаб разделения зарядов
– электронной поляризационной длиной. Можно найти аналогичные
величины, принимая, что разделение зарядов вызывается движением ионов,

7
тогда получается ионная плазменная частота. Поскольку электроны
подвижнее ионов, то электронная плазменная частота важнее ионной. Если
говорят просто о плазменной частоте, то имеют в виду электронную
плазменную частоту.
3. Идеальность плазмы
В плазме одновременно взаимодействует громадное число частиц.
Этим плазма резко отличается от обычных газов, в которых частицы
взаимодействуют друг
с другом в основном только при парных
столкновениях. Этим свойством плазма обязана дальнодействию
кулоновских сил, вовлекающих во взаимодействие множество частиц.
В плазме средняя потенциальная энергия взаимодействия частиц
ничтожна в сравнении с их кинетической энергией. Поэтому тепловое
движение в плазме и идеальном газе обладает большим сходством. Благодаря
этому термодинамические свойства плазмы с
хорошей точностью
описываются уравнением состояния идеального газа. Плазма,
удовлетворяющая этому условию относительно взаимодействия заряженных
частиц, называется идеальной плазмой.
Условие идеальности плазмы можно записать в виде:
Tk
U
вз
⋅
1, или
3
0
6
e
)Tk4(
en
⋅⋅ε⋅π
⋅
1. (11)
Далее будем иметь дело только с идеальной плазмой.
4. Электростатическое экранирование

8
Рассмотрим электростатическое экранирование отдельной заряженной
частицы в плазме. В пустом пространстве вокруг частицы с зарядом
ez
⋅
электростатический потенциал:
r
ez
4
2
0
⋅
⋅
ε⋅π
=ϕ
.
В плазме заряженная частица вызывает поляризацию окружающей
плазмы: вокруг такой частицы скапливаются частицы противоположного
знака, экранирующие поле частицы. Экранированный потенциал можно
вычислить с помощью теории Дебая, развитой им первоначально для
растворов сильных электролитов. Эта теория основана на представлении о
самосогласованности поля: находят такое распределение электрического
поля, которое создаёт распределение частиц,
возбуждающее в свою очередь
заданное поле.
Запишем уравнение Пуассона:
e
0
1
ρ⋅
ε
−=ϕΔ
(12)
и распределение Больцмана:
)
Tk
ez
exp(nn
k
kk
⋅
ϕ
⋅
⋅
−⋅=
, (13)
здесь
k
n
– концентрация частиц с зарядовым числом
k
z
в точке с
потенциалом
ϕ
;
k
n
– концентрация тех же частиц в точке с нулевым потенциалом (её
приравнивают к средней концентрации, взятой по всему объёму).
Индексом
k
отмечены все частицы, включая электроны, для которых
1z
k
−=
. Средние концентрации удовлетворяют условию
квазинейтральности:
0zn
k
k
k
=
⋅
∑
. (14)
Объёмный заряд:

9
∑
⋅
⋅
=
ρ
k
kke
zne
. (15)
Запишем нелинейное уравнение самосогласованного поля:
∑
⋅
ϕ
⋅
⋅
−⋅⋅⋅
ε
−=ϕΔ
k
k
kk
0
)
Tk
ez
exp(zn
e
. (16)
Однако в таком нелинейном виде пользоваться уравнением не имеет
смысла. Дело в том, что распределение Больцмана даёт вероятность
нахождения частицы в точке с потенциалом
ϕ
, то есть среднее по времени
значение концентрации, но мгновенные концентрации случайным образом
меняются (флуктуируют) вокруг этого среднего значения, вызывая
соответствующие флуктуации потенциала. Если в (16) под
ϕ
подразумевать
среднее по времени значение
ϕ
, то окажется, что в правой части среднее
значение функции заменено функцией от среднего значения, что допустимо
только для линейных функций. Поэтому (16) может быть использовано
только в линейном приближении. Для линеаризации раскладываем в правой
части (16) экспоненциальные функции в ряд, сохраняя только линейные
члены, получим линейное уравнение самосогласованного поля:
∑
⋅
ϕ
⋅
⋅
−⋅⋅⋅
ε
−=ϕΔ
k
k
kk
0
)
Tk
ez
1(zn
e
и учитывая (14), приходим к выражению:
∑
ϕ⋅⋅⋅
⋅⋅ε
=ϕΔ
k
2
kk
0
2
zn
Tk
e
. (17)
Решение уравнения (17) для симметричного распределения
потенциала вокруг точечного заряда имеет вид:
r
e
r
C
⋅ℵ−
⋅=ϕ
, (18)
где
ℵ
– постоянная экранирования:

10
∑
⋅⋅
⋅⋅ε
=ℵ
k
2
k
z
k
n
Tk
0
2
e
. (19)
(
x1
x
e +≈
;
в сферических координатах:
2
2
222
2
2
sinr
1
)(sin
sinr
1
)
r
r(
rr
1
ϕ∂
∂
⋅
θ⋅
+
θ∂
∂
⋅θ
θ∂
∂
⋅
θ⋅
+
∂
∂
⋅
∂
∂
⋅=Δ
).
Постоянная
С
в (18) должна быть такой, чтобы на малых расстояниях
потенциал стремился к значению
ϕ
, определяемому для частицы в пустом
пространстве. Отсюда следует окончательное выражение для
экранированного потенциала вокруг заряженной частицы в плазме:
r
0
e
r
ez
4
1
⋅ℵ−
⋅
⋅
⋅
ε⋅π
=ϕ
. (20)
Величина
ℵ
=
1
l
D
называется длиной экранирования или дебаевской
длиной (радиус Дебая-Хюккеля). Легко видеть, что она получается из
введённых выше пространственных масштабов разделения зарядов
k
d
по
правилу сложения обратных квадратов:
∑
=
k
2
k
2
D
d
1
l
1
. (21)
Поэтому длину экранирования можно рассматривать как
пространственный масштаб разделения зарядов или поляризационную длину
для всей плазмы в целом.
Теперь можно дать определение плазмы, в котором устанавливается
количественный смысл её квазинейтральности.
Плазма – это ионизованный газ, для которого дебаевский радиус мал в
сравнении с линейным масштабом области, занимаемой газом. Такое
определение дано
И. Ленгмюром.
