Лекции - Физика плазмы
Подождите немного. Документ загружается.

71
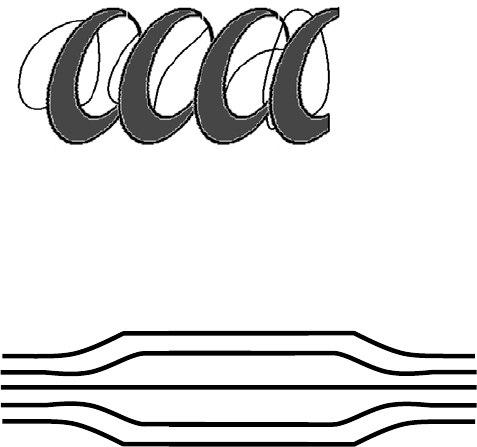
силовые линии магнитного поля
Если внутри плазмы нет стабилизирующего поля, то перестановка
местами плазмы и магнитных силовых линий тем выгоднее энергетически,
чем резче граница. В этом случае размытие границы стабилизирует плазму.
Но при наличии в плазме стабилизирующего поля, перпендикулярного
внешнему, размытие границы оказывает
противоположное действие. В этом случае
диффузия магнитного поля приводит к
перемешиванию взаимно
перпендикулярных
полей. В зоне размытия вместо "сетки" получается винтовое поле. Между
винтовыми силовыми линиями плазма может просачиваться. Получающиеся
возмущения имеют вид винтовых желобков, направленных вдоль винтовых
силовых линий. Желобковая
неустойчивость препятствует
удержанию плазмы в
адиабатических ловушках с
магнитными пробками (зеркалами). В области перехода от постоянного
основного к более сильному пробочному
полю силовые линии неизбежно
выпуклы наружу. В этой области языки плазмы просачиваются между
желобками, растянутыми вдоль силовых линий, что приводит к уходу
плазмы на стенку. Для борьбы с желобковой неустойчивостью предлагается
"примораживать" концы силовых линий к металлическим проводникам.

72
ТЕМА 6
КОЛЕБАНИЯ И ВОЛНЫ В ПЛАЗМЕ
ЛЕКЦИЯ 10
КОЛЕБАНИЯ И ВОЛНЫ В ПЛАЗМЕ
1. Колебания в холодной плазме
Холодной называется плазма, у которой газовое давление мало по
сравнению с магнитным:
2
0
B
l2
⋅
μ
⋅
=β 1.
Если это условие выполнено, то при рассмотрении большинства
вопросов, относящихся к колебаниям плазмы, можно полностью пренебречь
тепловым движением и рассматривать только усредненное движение под
действием внешних полей. Будем пренебрегать также столкновениями и
всеми процессами, приводящими к затуханию колебаний, то есть к
диссипации энергии.
Теория колебаний холодной плазмы заключается в совместном
рассмотрении уравнений движения проводящей среды и уравнений
Максвелла.
Применяя операцию
rot к обоим частям уравнения:
t
B
Erot
∂
∂
−=
r
r
,
получим:
Brot
t
Erotrot
r
r
∂
∂
−=
.
Подстановка уравнения:
t
E
jBrot
000
∂
∂
⋅ε⋅μ+⋅μ=
r
r
r
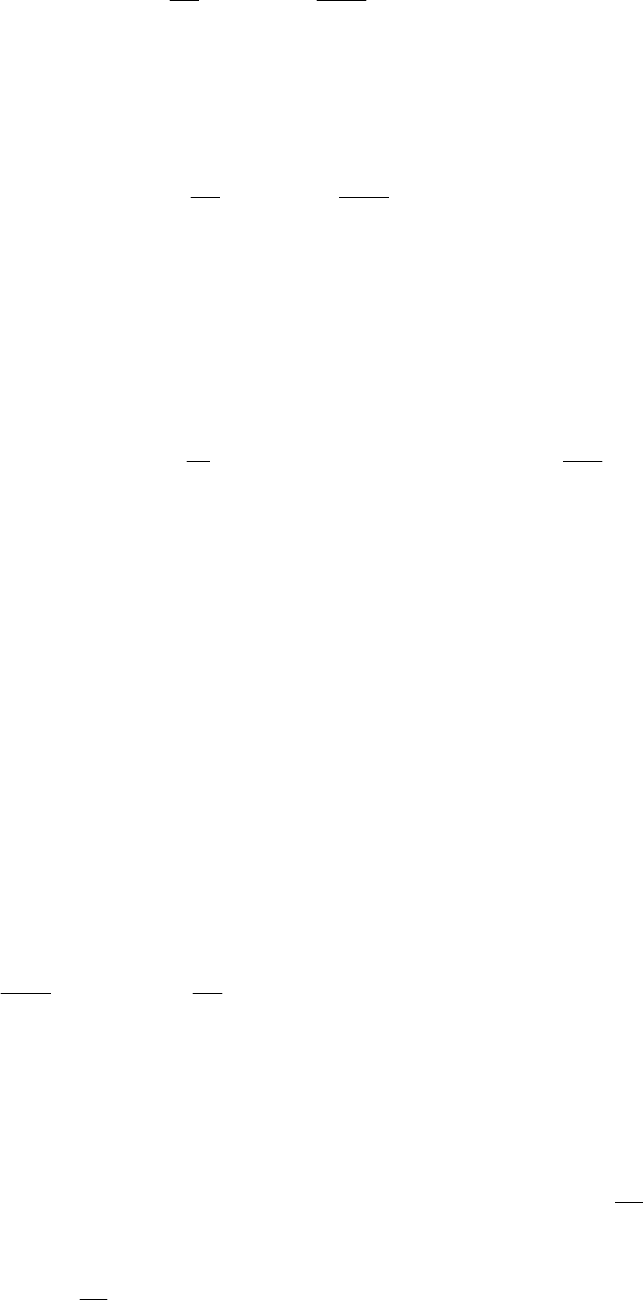
73
даёт:
2
2
000
t
E
t
j
Erotrot
∂
∂
⋅ε⋅μ−
∂
∂
⋅μ−=
r
r
r
.
Раскрывая операцию
rotrot по формулам векторного анализа, приходим к
результату:
2
2
000
t
E
t
j
EdivE
∂
∂
⋅ε⋅μ+
∂
∂
⋅μ=∇−Δ
r
r
rrr
.
В плоской волне любая величина
f
зависит от координат и времени как:
))trk(iexp(ff ⋅ω−⋅⋅⋅=
r
r
)
,
где
f
)
– комплексная амплитуда.
Фазовая скорость волны
k
u
ф
ω
=
, групповая скорость
dk
d
u
гр
ω
=
. В
анизотропных средах частоты связаны не только с величиной, но и с
направлением волнового вектора, то есть дисперсионное уравнение имеет
вид:
0)k,k,k,(F
321
=
ω
,
где
1
k
,
2
k
и
3
k
– составляющие волнового вектора.
В линейном приближении уравнения для комплексных амплитуд
f
)
имеют такой же вид, что и для величин
f
. Для плоской волны имеем:
EkE
2
r
r
⋅
−
=Δ , )Ek(kEdiv
r
r
r
r
r
⋅⋅−=∇ ;
E
t
E
2
2
2
r
r
⋅ω−=
∂
∂
, ji
t
j
r
r
⋅ω⋅−=
∂
∂
.
Тогда можно записать:
Eji)Ek(kEk
2
000
2
r
r
r
r
r
r
⋅ω⋅ε⋅μ+⋅ω⋅μ⋅=⋅⋅−⋅
. (1)
При рассмотрении линейных колебаний лагранжеву производную
dt
d
можно заменить частной
t
∂
∂
и в произведении
[
]
B,v
r
r
пренебречь

74
собственным полем волны B
~
r
, то есть заменить B
r
на постоянное внешнее
магнитное поле
0
B
r
. Уравнение движения плазмы принимает вид с учетом
сделанных допущений:
[
]
0
B,j
1
t
v
r
r
r
⋅
ρ
=
∂
∂
. (2)
Обобщенный закон Ома запишем в виде:
[]
[
]
00
2
B,j
m
e
)B,vE(
m
en
t
j
r
r
r
r
r
r
⋅−+⋅
⋅
=
∂
∂
. (3)
Система уравнений (2) и (3) совпадает с системой уравнений
магнитной гидродинамики для идеального проводника, из которых
выброшены силы давления. В соответствии с этим приближение холодной
плазмы называют иногда гидродинамическим приближением.
Введём характерные частоты:
- плазменную частоту
m
en
0
2
0
⋅ε
⋅
=ω
,
- циклотронные частоты
m
Be
0
e
⋅
=ω
M
Bez
0
i
⋅
⋅
=ω
.
Если не пренебрегать массой электрона по сравнению с массой иона,
то плазменная частота определяется так:
2
i0
2
e0
2
0
ω
+
ω
=
ω
,
где
m
en
0
2
e
2
e0
⋅ε
⋅
=ω
,
M
ezn
0
22
i
2
i0
⋅ε
⋅
⋅
=ω
.
Учитывая условие электронейтральности
ie
nznn ⋅=
=
, получим:
)
M
mz
1(
m
en
0
2
2
0
⋅
+⋅
⋅ε
⋅
=ω
.
Эта величина настолько мало отличается от электронной плазменной
частоты, что в дальнейшем не будем их различать. Тогда:

75
[]
[
]
h,jB,vE(
t
j
e0
2
00
rr
r
r
r
r
⋅ω−+⋅ω⋅ε=
∂
∂
, (4)
где
h
r
– единичный вектор в направлении магнитного поля.
Рассмотрение и описание всех типов колебаний в холодной плазме
сводится к совместному решению системы уравнений (1), (2) и (4). При
выводе этой системы сделаны следующие допущения:
1) плазму считаем полностью ионизованной;
2) амплитуды всех переменных величин в волне полагаются малыми,
чтобы можно было пренебречь всеми квадратичными членами (линейное
приближение);
3) тепловое (газовое) давление считается малым по сравнению с
магнитным давлением (приближение холодной плазмы);
4) пренебрегаем всеми диссипативными процессами (приближение
идеальной плазмы;
5) отбрасываются члены порядка отношения массы электрона к массе
иона. Это допустимо, если приближение проведено аккуратно в
математическом отношении.
2. Волны в плазме без магнитного поля
Если магнитное поле
отсутствует, то уравнение (4) сводится к виду:
E
i
t
j
2
00
r
r
⋅
ω
ω⋅ε⋅
=
∂
∂
,
соответственно из уравнения (1) получим:
E
cc
)Ek(kEk
2
2
0
2
2
2
r
r
r
r
r
⋅
⎟
⎠
⎞
⎜
⎝
⎛
ω
+
ω
=⋅⋅−⋅
,
где
00
2
1
c
ε⋅μ
=
.

76
Произвольную волну в плазме без магнитного поля можно разложить
на две составляющие: продольную (
k
r
E
r
) и поперечную ( Ek
r
r
⊥ ). Для
продольной волны
Ek)Ek(k
2
r
r
rr
⋅=⋅⋅
, тогда из полученного соотношения
следует:
2
0
2
ω=ω
. Это электростатические плазменные колебания, которые в
случае холодной плазмы возможны только на фиксированной плазменной
частоте.
Для поперечных волн
0)Ek( =⋅
r
r
, тогда
2
0
222
ck ω−ω
=
⋅
.
Полученное выражение – дисперсионное уравнение для
распространения электромагнитных волн в плазме без магнитного поля.
Распространение волн возможно при
2
0
2
ω
>
ω
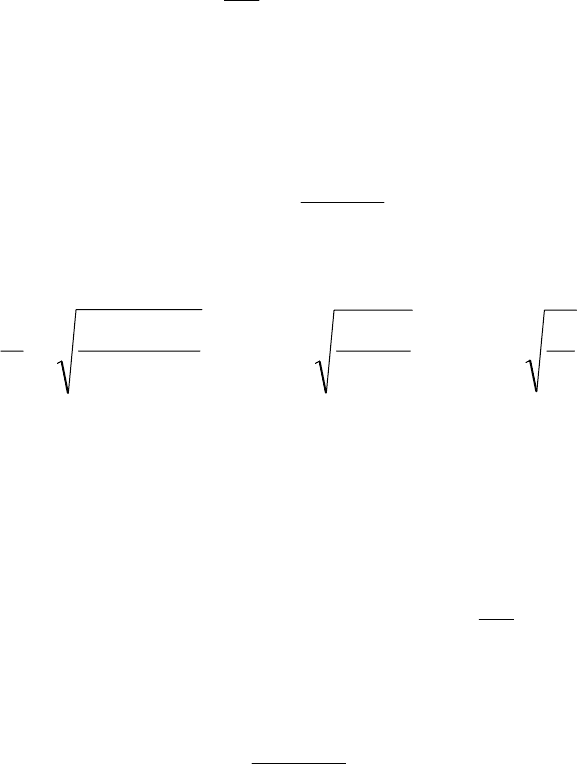
. Для
2
0
2
ω<
ω
волновое число
становится мнимым, то есть волна отражается от границы плазмы. Фазовая
скорость:
2
0
2
2
ф
c
R
u
ω−ω
ω
⋅=
ω
=
.
В области, где фазовая скорость вещественна (
2
0
2
ω>ω
), она всегда
больше скорости света и при приближении к плазменной частоте стремится к
бесконечности. Групповая скорость:
ф
2
2
гр
u
ck
cu =
ω
⋅=
,
то есть
2
грф
cuu
=
⋅
.
Групповая скорость всегда меньше скорости света. При частотах
ω
0
ω
как фазовая, так и групповая скорости стремятся к скорости света:
волна распространяется, как в пустоте. При стремлении частоты волны к
плазменной частоте фазовая скорость стремится к бесконечности, а
групповая – к нулю.
77
3. Распространение волн при наличии магнитного поля
Кажущаяся простой система векторных уравнений оказывается в
действительности для произвольного направления распространения волн
довольно громоздкой.
Рассмотрим сначала несколько простых случаев:
а) при распространении волны поперек магнитного поля или при
распространении вдоль магнитного поля, как показывает анализ, колебания с
электрическим полем, поперечным магнитному, отщепляются, то
есть
представляют собой независимые ветви колебаний. Магнитное поле на эти
ветви колебаний не действует.
Для колебаний с электрическим полем, параллельным магнитному
полю, когда
ll
2
Ek)Ek(k
r
r
rr
⋅=⋅⋅
, выполняется условие
2
0
2
ω=ω
. Это значит,
что колебания, поляризованные вдоль магнитного поля и
распространяющиеся продольно, представляют собой электростатические
плазменные колебания.
Для волн, распространяющихся поперек магнитного поля, не
поляризованных вдоль него, дисперсионное уравнение имеет вид:
2
0
222
ck
ω
−
ω
=
⋅
.
Эта ситуация тождественна рассмотренной при отсутствии
магнитного поля.
Рассмотренные типы колебаний, поляризованные вдоль магнитного
поля и распространяющиеся вдоль и поперек него, являются единственными,
на которые магнитное поле в приближении холодной плазмы не действует.
б) Магнитогидродинамические волны.
Рассмотрим волны, распространяющиеся вдоль магнитного поля при
произвольном направлении поляризации. Такую волну можно разложить
на
две независимые волны, у одной из которых электрическое поле
параллельно, а у другой – перпендикулярно к магнитному. Волна, у которой
78
как направление распространения, так и направление поляризации
параллельны внешнему магнитному полю, в холодной плазме вырождается в
плазменные колебания фиксированной частоты
0
ω
=
ω
.
Перейдём теперь к волне, распространяющейся вдоль магнитного
поля, но поляризованной поперёк него. Для этой волны
0)Ek( =⋅
r
r
, тогда:
jiE
с
Ek
0
2
2
2
r
r
r
⋅ω⋅μ⋅+⋅
ω
=⋅
. (*)
Рассмотрим сначала предельную область очень низких частот
ω
i
ω
.
Для этой области получается очень простое дисперсионное уравнение:
22
22
0
ei
ck
⋅
ω
⋅
ω
=ω⋅ω
,
откуда фазовая скорость волны:
A
0
0
i
0
0
2
0
2
ei
ф
ucB
Mn
cB
c
k
u =
ρ
ε
⋅⋅=
⋅
ε
⋅⋅=
ω
⋅ω⋅ω
=
ω
=
,
где
Mn
i
⋅≈ρ
– плотность плазмы.
Такие волны называются альфвеновскими или
магнитогидродинамическими, а скорость
A
u
– альфвеновской скоростью.
Пренебрегая током смещения, то есть членом
E
с
2
2
r
⋅
ω
в уравнении (*),
запишем:
j
k
i
E
2
0
r
r
⋅
ω
⋅
μ
⋅
=
,
то есть
E
r
j
r
.
Предельная область
ω
i
ω
полностью описывается уравнением
магнитной гидродинамики, и формулу для
A
u
легко получить из модели
идеально проводящей области. Запишем линеаризованное уравнение
движения:

79
[
]
0
B,j
1
t
v
r
r
r
⋅
ρ
=
∂
∂
;
или:
[
]
h,j
1
vi
r
r
r
⋅
ρ
=⋅ω⋅−
.
Следовательно:
[
]
0
2
0
22
B,E
ck
v
r
r
r
⋅
ω⋅ρ
ε
⋅
⋅
=
.
Используя далее условие идеальной проводимости
[
]
0
B,vE
r
r
r
−=
, и учитывая,
что
0
BE
rr
⊥
, получим дисперсионное уравнение:
[
][]
(
)
)vB(BBv
ck
B,v,B
ck
v
00
2
0
2
0
22
00
2
0
22
r
rr
r
r
r
r
r
⋅⋅−⋅⋅
ω⋅ρ
ε
⋅
⋅
=⋅
ω⋅ρ
ε⋅
⋅
=
,
2
0
2
0
22
Bv
ck
v ⋅⋅
ω⋅ρ
ε
⋅
⋅
=
rr
,
или:
2
2
00
22
Bck
1
ω⋅ρ
⋅
ε
⋅
⋅
=
.
Тогда фазовая скорость:
ρ
ε
⋅⋅=
ω
=
0
0A
cB
k
u
.
Условие
[
]
0
B,vE
r
r
r
−=
обеспечивает вмороженность магнитного поля.
Рассмотрим физическую картину магнитогидродинамических волн.
Они могут рассматриваться как поперечные колебания силовых линий
вместе с плазмой, в которую они вморожены. В области низких частот
(
ω
i
ω
), магнитогидродинамические волны распространяются с поперечной
скоростью, то есть дисперсия отсутствует и групповая скорость равна
фазовой.
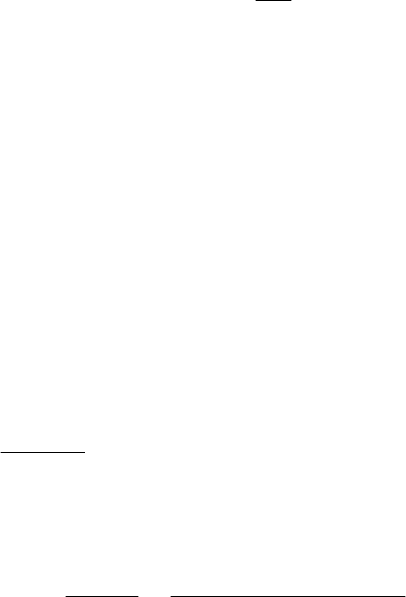
80
Чтобы можно было пренебречь током смещения, необходимо, чтобы
Mn
i
⋅
2
00
B⋅ε
. Преобразуем это условие к виду:
2
i
cMn
⋅
⋅
0
2
0
B
μ
,
то есть магнитная энергия плазмы должна быть мала по сравнению с
энергией поля. При малой плотности плазмы или очень сильном магнитном
поле это условие может не выполняться. В этих случаях простое
дисперсионное уравнение должно быть заменено более сложным
соотношением. Если для волн, распространяющихся вдоль магнитного поля,
условие
ω
i
ω
не выполняется, то возникает дисперсия и проявляются
гиротронные свойства плазмы. Дисперсионное уравнение имеет вид:
0
ck
e
2
ei
22
22
0
=ω⋅ω±ω+ω⋅ω−
⋅
ω⋅ω
.
Для квадрата показателя преломления плазмы получим:
e
2
ei
2
0
2
22
2
ck
N
ω⋅ω±ω−ω⋅ω
ω
=
ω
⋅
=
,
откуда следует, что при двух частотах, обращающих в ноль знаменатель,
∞→N
. Эти частоты называются резонансными (или частотами аномальной
дисперсии). Частоты аномальной дисперсии равны электронной и ионной
циклотронным частотам. Особенностью таких волн является круговая
поляризация, поэтому их называют волнами с круговой поляризацией. Двум
знакам в дисперсионном уравнении отвечают две волны, вращающиеся в
противоположных направлениях. Одна из них называется обыкновенной
волной. У обыкновенной
волны электрический вектор вращается в том же
направлении, как и отрицательный заряд в магнитном поле.
Суперпозицией двух волн, поляризованных по кругу в
противоположных направлениях, можно получить линейно поляризованную
волну. Но в области
ei
ω
<
ω
<
ω
способны распространяться только
необыкновенные волны и, следовательно, линейная поляризация
