Лекции - Электродинамика и распространение радиоволн (тексты лекций)
Подождите немного. Документ загружается.

то любая щель, прорезанная в боковой стенке волновода параллельно оси 0z
будет излучающей, в то время как щель, прорезанная посередине широкой
стенки волновода параллельно оси 0z – неизлучающей, и т.д.
6.4.6 Структуры полей Н-волн высших типов в прямоугольном
волноводе
Анализ структуры электромагнитного поля любой Н-волны высшего
типа следует начинать с преобразования системы уравнений (6.54) или (6.55) с
учетом конкретных значений индексов m и n рассматриваемой волны. После
этого следует изобразить картины силовых линий векторов Е и Н данной
волны.
Большую помощь в решении этой задачи может оказать следующее
правило. Структуру поля волны Н
10
можно считать базовой при построении
картин силовых линий векторов Е иН собственных волн Н
m0
и Н
0n
. Так,
например, для волны Н
20
картина силовых линий векторов Е и Н в
поперечном сечении волновода получается путем двукратного воспроизведения
базовой структуры вдоль широкой стенки волновода (с учетом фазовых
соотношений соседних структур); для волны Н
30
- трехкратным
воспроизведением, и т. д. Для волны Н
01
базовая структура будет повернута на
угол 90°; для волны Н
02
– повернута на 90° и воспроизведена дважды и т.д.
(см. рис.6.8).
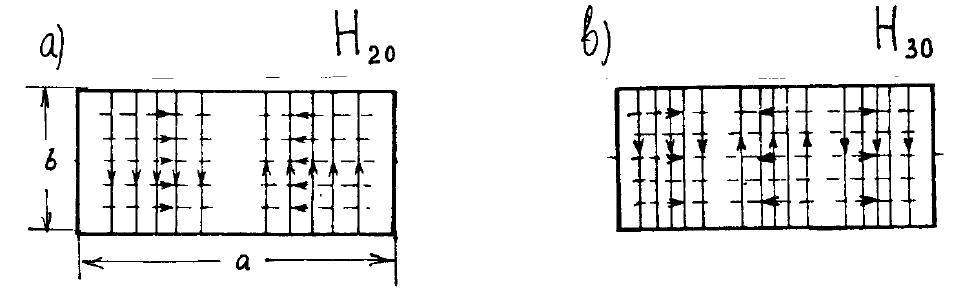
Рис.6.8. Силовые линии векторов Е и Н в поперечном сечении
прямоугольного волновода : а - для волны Н
20
, b - для волны Н
30
Несколько сложнее решается задача построения картины силовых линий
векторов Е и Н собственных волн, у которых индексы m и n оба не равны
нулю. В этом случае необходимо сначала построить картину силовых линий
волны Н
11
, которая затем, в зависимости от конкретных значений индексов m
и n, будет воспроизводиться требуемое число раз вдоль широкой и узкой
стенок волновода. Таким образом, для собственных волн типа Н
mn
базовой
структурой является структура поля волны Н
11
(см. рис.6.9).
71
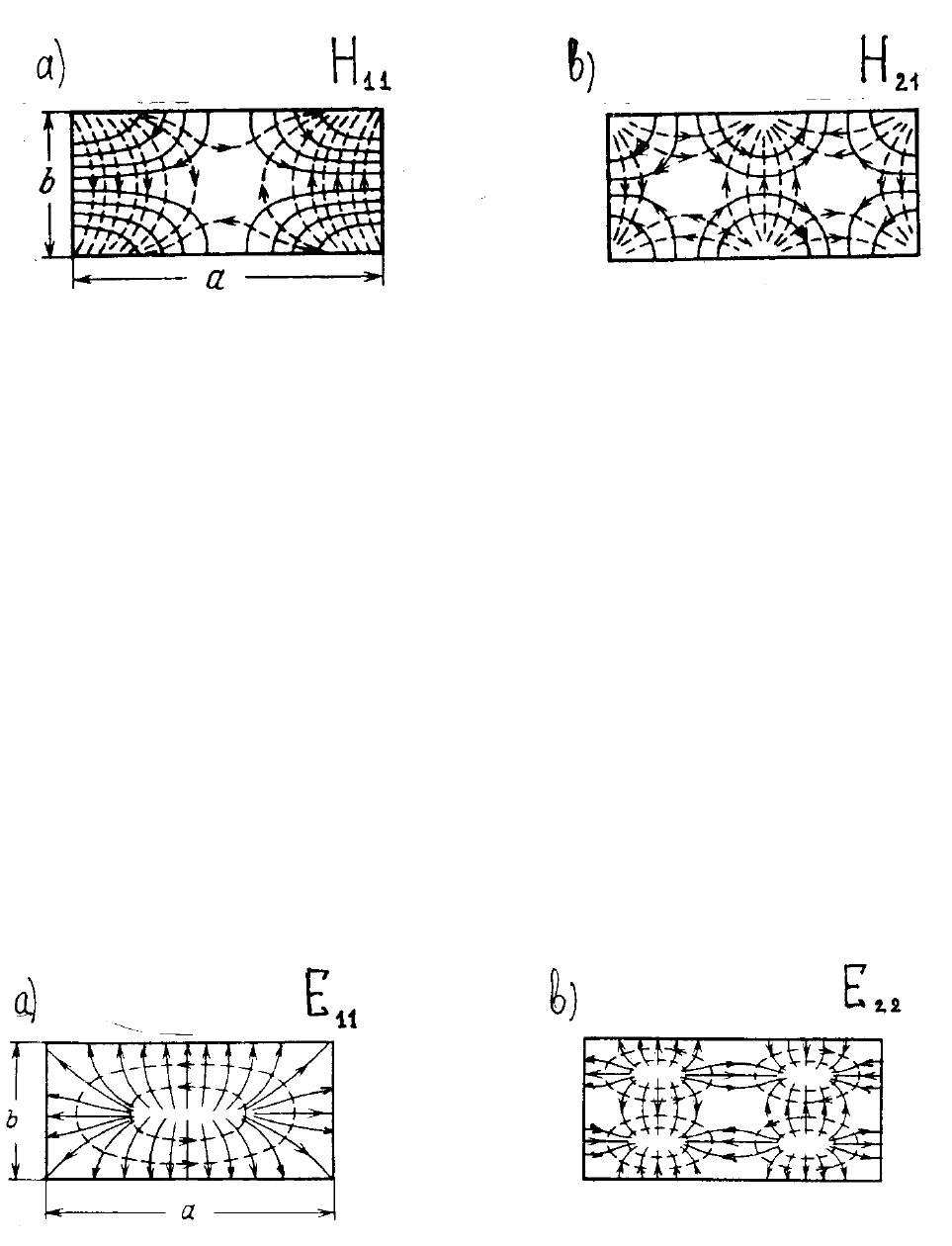
Рис.6.9. Силовые линии векторов Е и Н в поперечном сечении
прямоугольного волновода : а - для волны Н
11
, b - для волны Н
21
6.4.7 Структуры полей Е-волн в прямоугольном волноводе
Среди Е-волн наименьшую критическую длину волны имеет
собственная волна Е
11
(λ
кр
= 2ab / (a
2
+ b
2
)
0.5
). Система уравнений волны Е
11
имеет следующий вид :
.
Ε
x
= -j Е
0x
cos(x/a) sin(y/b) exp(-jКz).
.
Ε
y
= -j Е
0y
sin(x/a) cos(y/b) exp(-jКz).
.
Ε
z
=Е
0z
sin(x/a)sin(y/b)exp(-jКz). (6.66)
.
Η
x
= j H
0x
sin(x/a) cos(y/b) exp(-jКz).
.
Η
y
= -j H
0y
cos(x/a) sin(y/b) exp(-jКz).
.
Η
z
= 0.
Картина силовых линий векторов Е и Н этой волны в поперечном
сечении волновода изображена на рис 6.10. Структура поля волны Е
11
является
базовой при построении картин силовых линий векторов Е и Н собственных
волн Е
mn
(см. правило, изложенное в предыдущем подразделе).
Рис.6.10. Силовые линии векторов Е и Н в поперечном сечении
прямоугольного волновода : а - для волны E
11
, b - для волны E
22
72
6.4.8 Физический смысл индексов m и n , входящих в обозначение
собственных волн прямоугольного волновода
Знакомство со структурой полей собственных волн высших типов
облегчает понимание физического смысла индексов m и n, входящих в
обозначения этих волн.
Во всех собственных волнах поле в поперечном сечении волновода
представляет собой стоячие волны, пространственные периоды которых вдоль
осей 0x и 0y равны λ
x
и λ
y
соответственно. Индекс m показывает сколько
полуволн стоячей волны укладывается вдоль широкой стенки волновода, а
индекс n – сколько полуволн стоячей волны укладывается вдоль узкой стенки
волновода.
Формально это заключение можно сделать на основании следующих
математических выкладок
λ
x
= 2π/k
x
= 2 π / (mπ/a) = 2a / m, λ
y
= 2π/k
y
= 2 π / (mπ/b) = 2b / m .
Отсюда m = a / (λ
x
/2) ; n = b / (λ
y
/2) .
6.5 Структура электромагнитного поля Е- и Н-волн,
распространяющихся в круглом волноводе
Круглым волноводом называют односвязный металлический волновод,
поперечное сечение которого имеет форму круга. Стандартные круглые
волноводы представляют собой латунные или дюралевые трубы круглого
поперечного сечения, диаметры которых соответствуют ГОСТированным
числовым рядам.
Решение системы уравнений Максвелла для круглого волновода во
многом аналогично уже знакомому нам решению этих уравнений для
волновода прямоугольного. Так же как и в рассмотренном случае уравнения
Максвелла должны быть записаны в форме (1), а их решение должно
удовлетворять граничному условию (2). Так же как и в рассмотренном случае
решение этих уравнений мы будем искать в виде суперпозиции плоских
неоднородных Е- и Н-волн, распространяющихся вдоль волновода. Так же как
и в рассмотренном случае волновые уравнения мы будем решать только для
продольных составляющих векторов Е иН , а поперечные составляющие
этих векторов находить с помощью уравнений связи. Так же как и в
рассмотренном случае зависимость продольных составляющих векторов Е и
Н от пространственной переменной z , направленной вдоль волновода, будет
иметь вид
(z) = A
.
Ζ
exp(-jКz)
Отличие состоит в том, что при определении зависимости продольных
составляющих векторовЕ иН от поперечных пространственных переменных,
уравнение (6.17) должно быть раскрыто и проинтегрировано в цилиндрической
системе координат, так как именно в этой системе одна из координатных
поверхностей может совпадать с внутренней поверхностью стенки круглого
волновода (см. выводы подраздела 6.3.3).
73
6.5.1 Системы уравнений для Е- и Н-волн в круглом волноводе
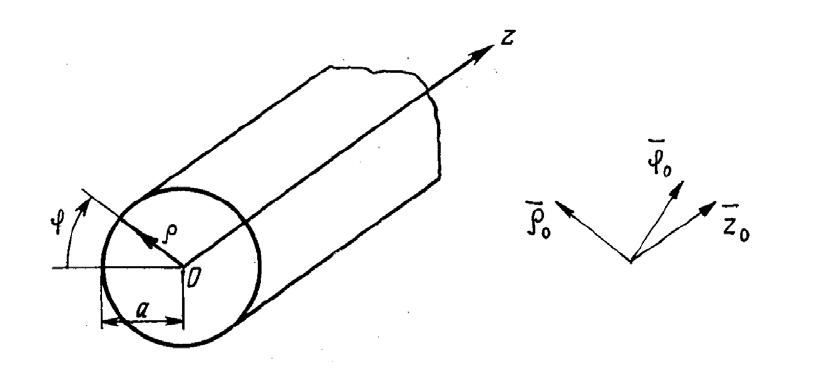
Ориентируем цилиндрическую систему координат (ρ,ϕ,z) так, чтобы ось
0z этой системы совпала с продольной осью симметрии круглого волновода
(см. рис.6.11). В этом случае функция Ψ (ξ,η) станет функцией Ψ (ρ,ϕ), а
уравнение координатной поверхности, совпадающей с внутренней
поверхностью стенки волновода, будет иметь вид ρ = а , где а – радиус
волновода.
Рис.6.11. Система координат круглого волновода
Граничное условие (2) в рассматриваемом случае трансформируется в
следующие соотношения:
Ε
⋅
z
|
ρ=а
=0,
(6.66)
⋅
Ε
ϕ
|
ρ=а
=0. (6.67)
Для дальнейших вычислений нам потребуются также граничные
условия для продольной составляющей
⋅
Η
z
или ее пространственных
производных, которые следует вывести из условий (6.66), (6.67) и уравнений
связи (6.9). Воспользовавшись условием (6.67) и вторым уравнением из
системы уравнений связи (6.9), имеем:
∂
.
Η
z
/∂ρ|
ρ=а
=0. (6.68)
Уравнение (6.17), записанное в цилиндрической системе координат
будет иметь следующий вид (см. выражение (6.12)):
∂
2
Ψ(ρ,ϕ)/∂ρ
2
+ (1/ρ)(∂Ψ(ρ,ϕ)/∂ρ)+(1/ρ
2
)(∂
2
Ψ(ρ,ϕ)/∂ϕ
2
) + æ
2
Ψ (ρ,ϕ) = 0.
(6.69)
Решение уравнения (6.69) будем осуществлять методом Фурье.
Представим функцию
Ψ (ρ,ϕ), зависящую от двух переменных ρ и ϕ , в виде
произведения двух функций Р (ρ) и Ф (ϕ) , каждая из которых зависит только от
одной из этих переменных:
Ψ(ρ,ϕ)=Р(ρ)⋅Ф(ϕ). (6.70)
Подставим (6.70) в (6.69) и после несложных преобразований получим
74
(ρ
2
/
Р(ρ))∂
2
Р(ρ)/∂ρ
2
+ (Р(ρ)/ρ) (∂Р(ρ)/∂ρ) + æ
2
ρ
2
= - (1/Ф(ϕ)) (∂
2
Ф(ϕ)/∂ϕ
2
).
(6.71)
Левая и правая части этого уравнения зависят от разных переменных,
поэтому оно может быть справедливо только в том случае, когда обе его части
равны одной и той же постоянной величине. Пусть этой постоянной величиной
будет некоторый коэффициент m
2
, физический смысл которого мы определим
позднее. В этом случае уравнение (6.71) может быть представлено в виде
системы из двух однородных дифференциальных уравнений
∂
2
Ф(ϕ)/∂ϕ
2
+m
2
Ф(ϕ)=0. (6.72)
(ρ
2
/Р(ρ))∂
2
Р(ρ)/∂ρ
2
+(Р(ρ)/ρ)(∂Р(ρ)/∂ρ)+æ
2
ρ
2
-m
2
=0. (6.73)
Уравнение (6.72) является уже хорошо нам знакомым однородным
дифференциальным уравнением второго порядка, решением которого могут
быть показательные или тригонометрические функции (см. (6.19) и (6.20) ).
Помня о том, что мы ищем распределение поля в поперечном сечении
волновода, где это поле представляет собой стоячие волны, оставляем решение
в виде суммы тригонометрических функций
Ф(ϕ)=М
1
cos(mϕ)+М
2
sin(mϕ). (6.74)
Так как рассматриваемый волновод обладает круговой симметрией, то
начало отсчета угла ϕ может быть выбрано произвольно, и формулу для Ф(ϕ)
можно записать в следующем виде :
Ф(ϕ)=Мcos(mϕ). (6.75)
Коэффициент m , входящий в аргумент косинуса в выражении (6.75),
может быть только целым числом, так как значение функции Ф(ϕ) не должно
изменяться при изменении ϕ на величину, кратную 2π. Таким образом
m=0,1,2,… (6.76)
Величина амплитудного коэффициента М зависит от параметров
источника, возбуждающего собственные волны в волноводе.
Займемся решением уравнения (6.73). После несложных преобразований
оно может быть представлено в следующем виде:
∂
2
Р(ξ)/∂ξ
2
+(1/ξ)(∂Р(ξ)/∂ξ)+(1-m
2
/ξ
2
)Р(ξ)=0, (6.77)
где ξ = æ⋅ρ - независимая переменная.
Уравнение (6.77) представляет собой хорошо известное в
математической физике уравнение Бесселя, решением которого являются
специальные функции Бесселя первого и второго рода порядка m ( J
m
и N
m
соответственно):
P(ξ)=AJ
m
(ξ)+BN
m
(ξ), (6.78)
где m -порядок функции Бесселя.
75
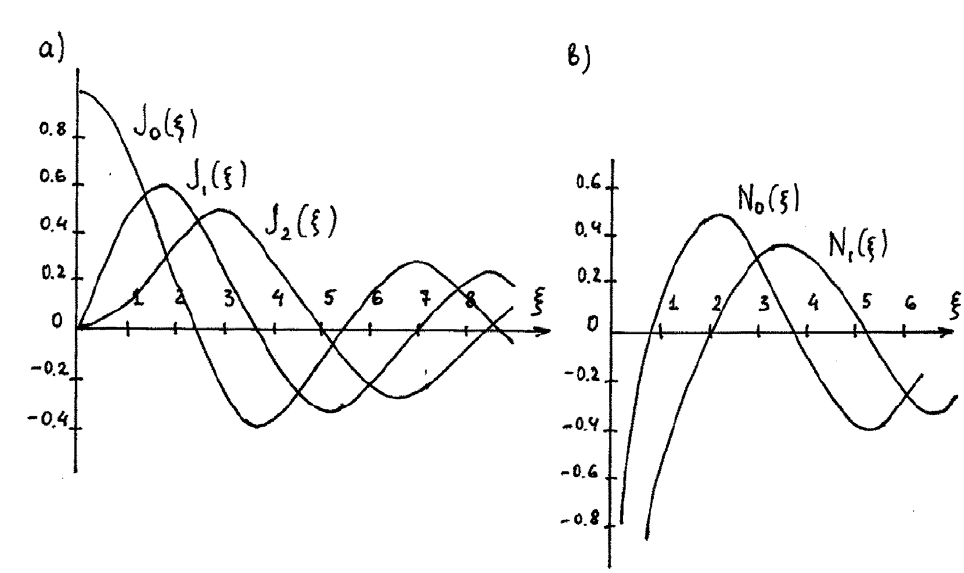
Рис.6.12. Графики функций : а - J
m
(ξ) , b - N
m
(ξ)
Графики функций J
m
(ξ) и N
m
(ξ) для различных значений m приведены на
рис.6.12. Вернувшись в выражении (6.78) к переменной æ⋅ρ, видим, что, исходя
из физических соображений, коэффициент В должен равняться 0, так как в
противном случае в центре волновода (при ρ = 0) напряженность
электрического или магнитного поля оказывается равной бесконечности. Таким
образом, приемлемым для рассматриваемого случая решением уравнения (6.77)
является:
P(æ⋅ρ)=AJ
m
(æ⋅ρ). (6.79)
Подставив (6.79) и (6.75) в выражение (6.70) и обозначив С = А⋅М,
получаем решение уравнения (6.69)
Ψ(ρ,ϕ)=СJ
m
(æ⋅ρ)cos(mϕ). (6.80)
В выражении (6.80) амплитудный коэффициент С зависит от параметров
источника, возбуждающего волновод, коэффициент m может принимать
целые положительные значения, включая 0 (см.(6.76)), а поперечное волновое
число æ должно быть определено из граничных условий. Напомним, что для
Е-волн функция Ψ(ρ,ϕ) эквивалентна составляющей
⋅
Ε
z
, а для Н-волн –
составляющей
⋅
Η
z
. Следовательно, в зависимости от типа собственной волны,
граничными условиями для функции Ψ (ρ,ϕ) будут либо (6.66), либо (6.68).
Определение поперечного волнового числа для Е-волн (æ
Е
).
Воспользуемся граничным условием (6.66). Подставим Ψ(ρ=а, ϕ) = 0 в
выражение (6.80):
0 = С J
m
(æ
Е
⋅а) cos (mϕ) . Отсюда æ
Е
⋅ а = ν
m n
,
76
где ν
m n
- корни функции J
m
(ξ) (напомним, что корнем функции
называется такое значение ее аргумента, при котором функция обращается в
ноль);
n - номер корня этой функции (n = 1. 2, 3… ).
Следовательно, æ
Е
= ν
m n
/ a . (6.81)
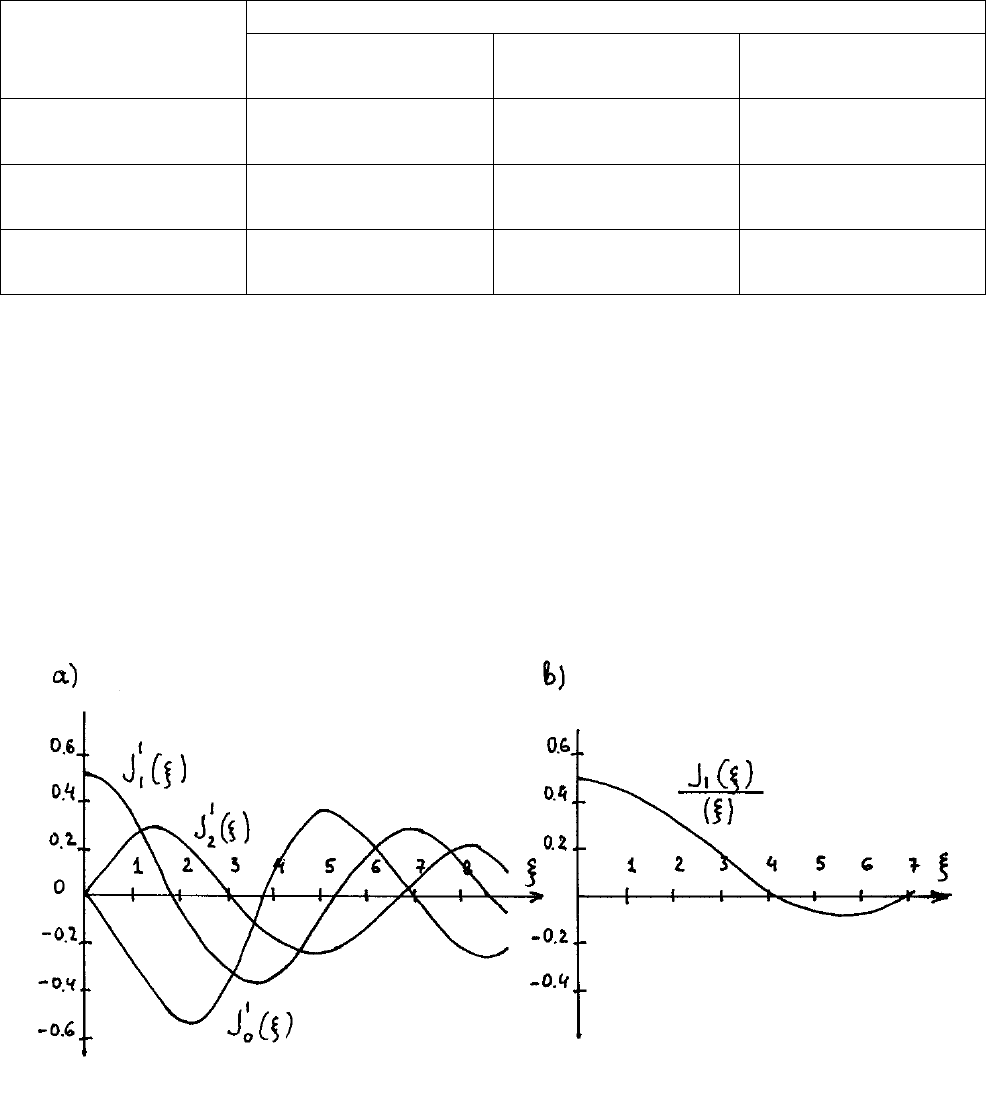
В табл.6.1 приведены численные значения некоторых корней функций
J
m
(ξ) (см. также графики на рис.6.12)
Таблица 6.1
m
n
0
1
2
1
2.405
3.832
5.136
2
5.520
7.016
8.417
3
8.654
10.173
11.620
Определение поперечного волнового числа для Н-волн (æ
Н
). Так как в
данном случае известны граничные условия не для самой составляющей
⋅
Η
z
а
лишь для ее первой производной ∂
.
Η
z
/∂ρ, то чтобы воспользоваться этими
граничными условиями необходимо продифференцировать функцию Ψ (ρ,ϕ)
по переменной ρ :
∂Ψ(ρ,ϕ)/∂ρ)=æ
Н
АJ′
m
(æ
Н
ρ), (6.82)
где J′
m
(æ
Н
ρ) первая производная функции J
m
(æ
Н
ρ) по переменной ρ
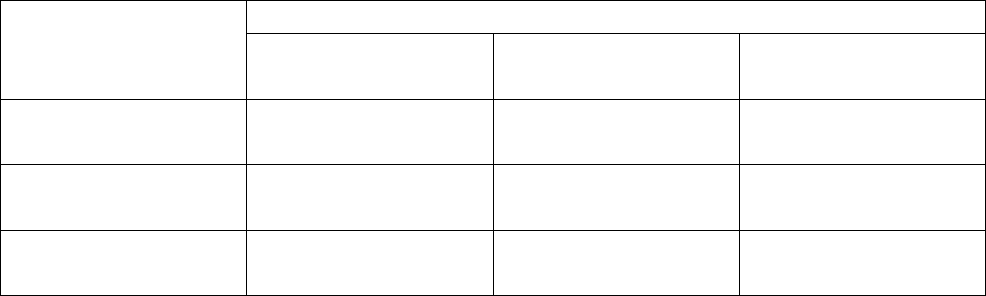
(график функции J′
m
(ξ) приведен на рис.6.13)
Рис.6.13. Графики функций : а - J′
m
(ξ) , b - J′
m
(ξ)/(ξ)
77
Теперь можно воспользоваться граничным условием (6.68). Подставим
∂Ψ (ρ,ϕ)/∂ρ |
ρ= а
= 0 в выражение (6.82) и получим следующее уравнение :
0 = æ
Н
А J′
m
(æ
Н
а). Отсюда æ
Н
а = χ
m n
,
где χ
m n
- корни функции J′
m
(ξ) ;
n - номер корня этой функции (n = 1, 2, 3 … ).
Следовательно , æ
Н
= χ
m n
/ а . (6.83)
В табл.6.2 приведены численные значения некоторых корней функции
J′
m
(ξ) (см. также график на рис.6.13) .
Таблица 6.2
m
n
0
1
2
1
3.832
1.841
3.054
2
7.016
5.331
6.706
3
8.536
9.969
10.173
Как следует из (6.81), (6.83), таб.6.1 и таб.6.2 в круглом волноводе, в
отличие от прямоугольного, поперечные волновые числа для Е- и Н-волн с
одинаковыми индексами не равны друг другу. Следовательно, и продольные
волновые числа для этих волн также будут отличаться друг от друга :
К
Е
= ( k
2
– (æ
Е
)
2
)
0.5
; К
H
= ( k
2
– (æ
H
)
2
)
0.5
. (6.84)
Вычислив æ
Е
и æ
Н
, можно записать формулы, определяющие
зависимость продольной составляющей
⋅
Ε
z
вектораЕ (для Е-волн) и
продольной составляющей
⋅
Η
z
вектораН (для Н-волн) от пространственных
координат, в следующем виде (см. выражения (6.14), (6.80), (6.81), (6.83) и
(6.84)):
⋅
Ε
z
(ρ,ϕ,z)=Е
0
J
m
(æ
Е
⋅ρ)cos(mϕ)exp(-jК
Е
z). (6.85)
⋅
Η
z
(ρ,ϕ,z)=Н
0
J
m
(æ
Н
⋅ρ)cos(mϕ)exp(-jК
Н
z). (6.86)
Теперь необходимо воспользоваться уравнениями связи (6.8) и (6.9) и
взяв первые производные по переменным ρ и ϕ от составляющих
⋅
Ε
z
и
⋅
Η
z
вывести формулы для поперечных составляющих векторов Е и Н .
В результате будут получены системы уравнений для векторов Е и Н
электрических и магнитных волн в круглом волноводе :
для Е-волн
.
Ε
ρ
= (- j К
E
/ æ
Е
) Е
0
J′
m
(æ
Е
⋅ρ) cos (mϕ) exp(-j К
E
z).
.
Ε
ϕ
= ( j К
E
/ æ
Е
) m Е
0
(J
m
(æ
Е
⋅ρ)/(æ
Е
⋅ρ)) sin (mϕ) exp(-j К
E
z).
78
.
Ε
z
=Е
0
J
m
(æ
Е
⋅ρ)cos(mϕ)exp(-jК
E
z).
(6.87)
.
Η
ρ
= (- j ωε
а
/ æ
E
) m Е
0
(J
m
(æ
Е
⋅ρ)/(æ
Е
⋅ρ)) sin (mϕ) exp(-j К
E
z).
.
Η
ϕ
= (- j ωε
а
/ æ
E
) Е
0
J′
m
(æ
Е
⋅ρ) cos (mϕ) exp(-j К
E
z).
.
Η
z
= 0.
Уравнения (6.87) могут быть записаны в более компактном виде
.
Ε
ρ
= - j Е
0ρ
J′
m
(æ
Е
⋅ρ) cos (mϕ) exp(-j К
E
z) = - j E
ρ
(ρ,ϕ) exp(-j К
E
z).
.
Ε
ϕ
= j Е
0ϕ
(J
m
(æ
Е
⋅ρ)/(æ
Е
⋅ρ)) sin (mϕ) exp(-j К
E
z) = j E
ϕ
(ρ,ϕ) exp(-j К
E
z).
.
Ε
z
=Е
0z
J
m
(æ
Е
⋅ρ)cos(mϕ)exp(-jК
E
z)=E
z
(ρ,ϕ)exp(-jК
E
z).
(6.88)
.
Η
ρ
= - j H
0ρ
(J
m
(æ
Е
⋅ρ)/(æ
Е
⋅ρ)) sin (mϕ) exp(-j К
E
z) = - j H
ρ
(ρ,ϕ) exp(-j К
E
z).
.
Η
ϕ
= - j H
0ϕ
J′
m
(æ
Е
⋅ρ) cos (mϕ) exp(-j К
E
z) = - j H
ϕ
(ρ,ϕ) exp(-j К
E
z).
.
Η
z
= 0.
Формулы для амплитуд составляющих векторов Е и Н поперечно-
магнитных волн (Е-волн) круглого волновода выглядят следующим образом :
Е
ρ
(ρ,ϕ) = Е
0ρ
J′
m
(æ
Е
⋅ρ) cos (mϕ) .
Е
ϕ
(ρ,ϕ) = Е
0ϕ
(J
m
(æ
Е
⋅ρ)/(æ
Е
⋅ρ)) sin (mϕ) .
E
z
(ρ,ϕ)=E
0z
J
m
(æ
E
⋅ρ)cos(mϕ). (6.89)
Н
ρ
(ρ,ϕ) =.Н
0ρ
J′
m
(æ
E
⋅ρ) cos (mϕ) .
Н
ϕ
(ρ,ϕ) = Н
0ϕ
(J
m
(æ
E
⋅ρ)/(æ
E
⋅ρ)) sin (mϕ) .
для Н-волн
.
Ε
ρ
= ( j ωµ
а
/ æ
Н
) m Н
0
(J
m
(æ
Н
⋅ρ)/(æ
Н
⋅ρ)) sin (mϕ) exp(-j К
Н
z).
.
Ε
ϕ
= ( j ωµ
а
/ æ
Н
) Н
0
J′
m
(æ
Н
⋅ρ) cos (mϕ) exp(-j К
Н
z).
.
Ε
z
=0.
(6.90)
.
Η
ρ
=.(- j К
Н
/ æ
Н
) Н
0
J′
m
(æ
Н
⋅ρ) cos (mϕ) exp(-j К
Н
z).
.
Η
ϕ
= ( j К
Н
/ æ
Н
) m Н
0
(J
m
(æ
Н
⋅ρ)/(æ
Н
⋅ρ)) sin (mϕ) exp(-j К
Н
z).
.
Η
z
= Н
0
J
m
(æ
Н
⋅ρ) cos (mϕ) exp(-j К
Н
z).
Уравнения (6.90) могут быть записаны в более компактном виде
.
Ε
ρ
= j Е
0ρ
(J
m
(æ
Н
⋅ρ)/(æ
Н
⋅ρ)) sin (mϕ) exp(-j К
Н
z) = j Е
ρ
(ρ,ϕ) exp(-j К
Н
z).
.
Ε
ϕ
= j Е
0ϕ
J′
m
(æ
Н
⋅ρ) cos (mϕ) exp(-j К
Н
z) = j Е
ϕ
(ρ,ϕ) exp(-j К
Н
z).
.
Ε
z
=0.
(6.91)
.
Η
ρ
=.- j Н
0ρ
J′
m
(æ
Н
⋅ρ) cos (mϕ) exp(-j К
Н
z) = - j Н
ρ
(ρ,ϕ) exp(-j К
Н
z).
.
Η
ϕ
= j Н
0ϕ
(J
m
(æ
Н
⋅ρ)/(æ
Н
⋅ρ)) sin (mϕ) exp(-j К
Н
z) = j Н
ϕ
(ρ,ϕ) exp(-j К
Н
z).
.
Η
z
= Н
0z
J
m
(æ
Н
⋅ρ) cos (mϕ) exp(-j К
Н
z) = Н
z
(ρ,ϕ) exp(-j К
Н
z).
Формулы для амплитуд составляющих векторов Е и Н поперечно-
электрических волн (Н-волн) круглого волновода выглядят следующим
образом :
Е
ρ
(ρ,ϕ) = Е
0ρ
(J
m
(æ
Н
⋅ρ)/(æ
Н
⋅ρ)) sin (mϕ) .
79
Е
ϕ
(ρ,ϕ) = Е
0ϕ
J′
m
(æ
Н
⋅ρ) cos (mϕ) .
Н
ρ
(ρ,ϕ)=Н
0ρ
J′
m
(æ
Н
⋅ρ)cos(mϕ). (6.92)
Н
ϕ
(ρ,ϕ) = Н
0ϕ
(J
m
(æ
Н
⋅ρ)/(æ
Н
⋅ρ)) sin (mϕ) .
Н
z
(ρ,ϕ) = Н
0z
J
m
(æ
Н
⋅ρ) cos (mϕ) .
Критические длины волн для собственых волн круглого волновода
могут быть рассчитаны по следующим формулам (см.выражение (6.32) :
λ
Е
кр
= 2π / æ
Е
,
λ
Н
кр
= 2π / æ
Н
. (6.93)
Анализ выражений (6.32), (6.81), (6.83), (6.93) и данных, приведенных в
таблицах 6.1 и 6.2, показывает, что волной низшего типа в круглом волноводе
является волна Н
11.
Исследуем структуру электромагнитного поля этой волны.
6.5.2 Структура поля волны Н
11
в круглом волноводе
Для волны Н
11
коэффициенты m и n равны единице, поперечное
волновое число æ
Н
= 1.84/а , а критическая длина волны λ
Н
кр
= 3.41 а .
Следовательно, формулы для амплитуд составляющих векторов Е и Н этой
волны будут выглядеть следующим образом (см. выражения (6.92)):
Е
ρ
(ρ,ϕ) = Е
0ρ
(J
1
(1.84ρ/a)/(1.84ρ/a)) sin ϕ .
Е
ϕ
(ρ,ϕ) = Е
0ϕ
J′
1
(1.84ρ/a) cos ϕ .
Н
ρ
(ρ,ϕ) =Н
0ρ
J′
1
(1.84ρ/a)cosϕ. (6.94)
Н
ϕ
(ρ,ϕ) = Н
0ϕ
(J
1
(1.84 ρ/a)/(1.84ρ/a)) sin ϕ .
Н
z
(ρ,ϕ) = Н
0z
J
1
(1.84ρ/a) cos (ϕ) .
Формулы для гармонических векторов Е иН волны Н
11
имеют
следующий вид :
Е=ρ
0
Е
ρ
(ρ,ϕ)cos(ωt–K
Н
z)+ϕ
0
Е
ϕ
(ρ,ϕ)cos(ωt – K
Н
z), (6.95)
Н = -ρ
0
Н
ρ
(ρ,ϕ) cos (ωt – K
Н
z) +ϕ
0
Н
ϕ
(ρ,ϕ) cos (ωt – K
Н
z) +
+z
0
Н
z
(ρ,ϕ)sin(ωt–K
Н
z), (6.96)
гдеρ
0
,ϕ
0
,z
0
– орты (единичные векторы) цилиндрической системы
координат, направленные по касательным к ее координатным линиям.
Учитывая, что пространственная переменная ρ изменяется внутри
волновода от 0 до а, получаем, что аргументы функций J
1
(1.84ρ/a) и J′
1
(1.84ρ/a),
определяющих зависимость амплитуд составляющих векторов Е и Н
собственной волны Н
11
от переменной ρ, изменяются от 0 (в центре волновода)
до 1.84 (в непосредственной близости к стенке волновода). Оценив, как ведут
себя эти функции при данных изменениях их аргументов, и помня, что
аргумент функций cos(1⋅ϕ) и sin(1⋅ϕ), описывающих зависимость
составляющих векторов Е и Н от пространственной переменной ϕ, в
рассматриваемом случае при изменении ϕ от 0 до 2 также изменяется от 0 до
2π, можно построить графические изображения силовых линий векторов Е и
Н собственной волны Н
11
.
80
