Лекции - Электродинамика и распространение радиоволн (тексты лекций)

Подождите немного. Документ загружается.

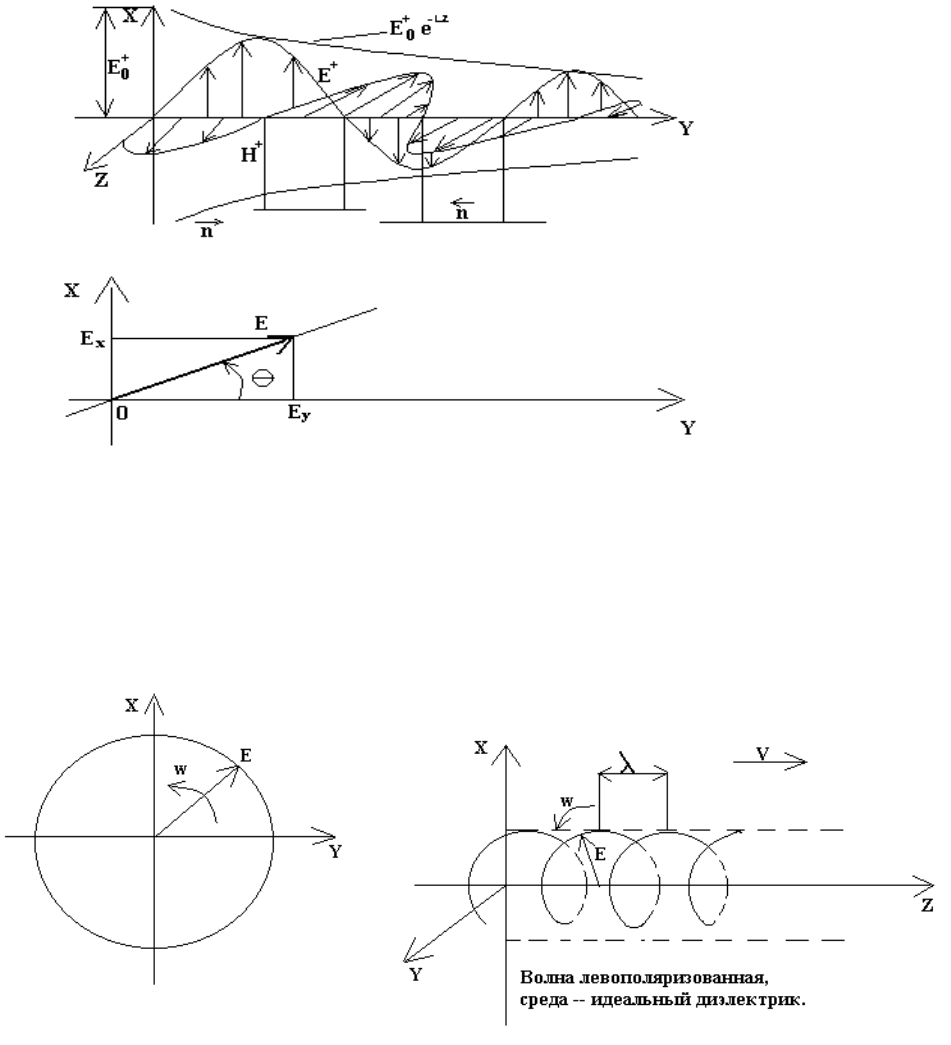
Рис.4.3 Падающая плоская волна в поглощающей среде.

Рис.4.4 Линейная поляризация (положение плоскости поляризации

относительно осей координат с течением времени не изменяется, угол θ =

const).

а) б)

Рис.4.5 Круговая поляризация (волна левополяризованная) :

а) изменение во времени вектора Е в плоскости z = const;

б) изменение в пространстве вектора Е в фиксированный момент

времени.

Рис.4.6 Эллиптическая поляризация (волна левополяризованная) ;

плоскость поляризации с течением времени вращается вокруг оси 0z с угловой

скоростью ω, угол θ = θ(t).

Вопросы для самопроверки

1.В чем заключается отличие волновых процессов от колебательных процессов в

радиотехнических цепях?

2.Какая дополнительная характеристика вводится для описания векторных волновых

процессов?

3.Какие виды поляризации принято рассматривать в задачах электродинамики?

4.Каковы основные свойства плоской волны?

5.Какой характер носит волновое число в различных средах?

6.В чем заключаются особенности распространения плоской волны в средах с

проводимостью?

7.Какова природа явления дисперсии при распространении плоской волны в

полупроводящей среде?

8.К чему приводит нелинейность и анизотропия среды при распространении плоской

волны?

5. Сферические волны в однородной среде. Излучение

В отличие от плоских электромагнитных волн, рассмотренных в

предыдущем разделе и представляющих собой математическую абстракцию,

сферические волны являются физически реализуемым и единственным из

возможных видов волновых процессов, который может распространяться в

свободном пространстве.

Общее выражение для сферической волны может быть записано в виде:

)(cos

sin

СС

−

, (5.1)

где С

– амплитуда любой составляющей электромагнитной волны;

r - расстояние до точки наблюдения из начала сферической системы

координат;

Θ - угловая координата сферической системы координат;

ω - круговая частота волнового процесса;

v - скорость распространения волнового процесса;

t - время.

При заданных значениях ω и t фаза колебаний будет зависеть только от

расстояния. Т.о. поверхности равных фаз сферической волны в пространстве

представляют собой сферы радиуса r. Поверхность же равных амплитуд будет

постоянна при

Θsin

= сonst, т.е. кривизна этой поверхности зависит от угла Θ.

Иными словами говоря, поверхности равных фаз и равных амплитуд в

сферической волне не совпадают и она является неоднородной.

Более подробное знакомство со свойствами сферической волны можно

получить, рассматривая особенности излучения электромагнитной энергии в

свободное пространство. На практике излучение электромагнитных волн

обеспечивается системой сторонних токов, протекающих в технических

устройствах, называемых антеннами. Для понимания процессов,

происходящих в реальных антеннах, крайне важно изучение особенностей

излучения так называемых элементарных излучателей, совокупностью которых

могут быть представлены указанные антенны. В качестве элементарных

излучателей принято рассматривать: элементарный электрический излучатель

(диполь Герца), элементарный магнитный излучатель (магнитная рамка),

элементарный поверхностный излучатель (элемент Гюйгенса).

5.1 Элементарный электрический излучатель

Элементарный электрический излучатель (диполь) - это проводник

малой электрической (по отношению к длине волны) длины, по которому

протекает переменный ток.. Малая электрическая длина диполя позволяет в

некотором приближении, тем более строгом, чем короче диполь, считать

амплитуду и фазу тока вдоль диполя постоянными, что существенно упрощает

решение задачи.

При рассмотрении данного вопроса принято полагать, что диполь

длиной l располагается в безграничной, однородной, изотропной,

непроводящей среде с параметрами ε

, µ

; плотность тока δ

ст

вдоль диполя

полагается известной, изменяющейся по гармоническому закону. Для решения

этой задачи удобно воспользоваться волновыми уравнениями для

электродинамических потенциалов, тем более, что для гармонических

процессов достаточно решить только одно уравнение для векторного

потенциала, а скалярный может быть найден из калибровочного соотношения

(см.2.16- 2.18).

Общее решение волнового уравнения для векторного потенциала имеет

вид:

jkr

ст

−

∫

, где V – объем, в котором расположены источники

поля (сторонний ток); r – расстояние от точки наблюдения до каждой точки

объема. Для случая элементарного электрического диполя интеграл в этом

выражении может быть легко вычислен, если полагать, что кроме постоянства

амплитуды тока вдоль диполя, еще и расстояние до точки наблюдения много

больше длины диполя. В этом случае можно считать, что r является величиной

постоянной для всех точек диполя и равной расстоянию до начала сферической

системы координат, в которой диполь и располагается (Рис 5.1).

Рис. 5.1

Окончательно учитывая, что объем элементарного диполя можно

представить в виде произведения его площади на длину, выражение для

векторного потенциала приобретает вид:

lIА

jkr

−

⋅=

. (5.2)

Здесь I- амплитуда тока вдоль диполя;

l- длина диполя.

Т.о. в любой точке пространства векторный потенциал параллелен

диполю, причем поле векторного потенциала и по амплитуде и по фазе

является сферическим. В сферической системе координат векторный

потенциал имеет две составляющие:

Θ−=Θ=

sin;cos

ээr

АААА

&&&&

, не зависящие от угла ϕ; составляющая же А

=0.

Следующий этап решения задачи состоит в отыскании векторов

НЕ , .

Используя (2.19-2.20), можно получить:

НН =

= Θ+

⋅

−

sin)

(

jkr

(5.3)

+= ErЕ

, где:

Θ+

⋅

−=

−

cos)

(

jЕ

jkr

πωε

, (5.4)

Θ−+

⋅

−=

−

sin)

(

jЕ

jkr

πωε

. (5.5)

В выражениях 5.3-5.5 : r

, Θ

- единичные орты сферической системы

координат; ω – частота переменного тока, протекающего по диполю.

Свойства поля электрического диполя.

Из полученных выражений можно видеть, что для сферической волны,

так же как и для плоской –

1. характер изменения поля зависит от свойств среды (вещественно,

либо комплексно волновое число k);

2. вектор магнитного поля Н имеет только одну составляющую,

поэтому его силовые линии являются окружностями, параллельными

экваториальной плоскости;

3. вектор напряженности электрического поля Е не имеет

составляющей Е

, поэтому его силовые линии лежат в меридиональных

плоскостях;

4. векторы напряженности электрического и магнитного полей в

любой точке пространства взаимно перпендикулярны;

5. фаза составляющих электромагнитного поля зависит только от

координаты r, поэтому поверхностями равных фаз поля излучения диполя

являются сферы;

6. амплитуды составляющих поля излучения зависят только от

координат Θ и r, поэтому относительно оси диполя электромагнитное поле

симметрично.

Зависимость поля излучения от угловых координат Θ, φ принято называть

функцией направленности диполя (в технике часто используется понятие

диаграмма направленности – графическое представление функции

направленности). Как следует из 5.3-5.5, амплитуды составляющих Е

и Нφ

пропорциональны sin Θ, а от угла φ не зависят. Т.о. пространственная

диаграмма направленности диполя представляет собой тороид.

Амплитуда составляющей Е

пропорциональна cosΘ и также не зависит

от угла φ, поэтому ее пространственная диаграмма направленности

представляет собой две соприкасающиеся сферы с максимумами излучения,

расположенными под углами Θ равными 0 и 180 градусам.

Поскольку амплитуда составляющих поля излучения диполя, кроме

зависимости от угловых координат, зависит еще от расстояния до точки

наблюдения, причем достаточно сложным образом, то все пространство вокруг

диполя в зависимости от расстояния принято делить на три характерные

области:

- ближнюю зону, где kr <<1 (2πr <<λ);

- промежуточную зону, где kr ≈ 1 (2πr ≈ λ);

- дальнюю зону, где kr >>1 (2πr >>λ).

В ближней зоне (зоне индукции, либо квазистационарной зоне) r столь

мало, что запаздыванием при распространении электромагнитной волны от

диполя до точки наблюдения можно пренебречь (можно пренебречь волновым

характером поля). Математически это означает, что в выражениях 5.3-5.5

фазовый множитель e

-jkr

≈1, в амплитудных множителях можно пренебречь

всеми слагаемыми, которые убывают быстрее, чем 1/r

для магнитного поля и

1/r

для электрического поля. Тогда выражения для составляющих поля

излучения диполя в ближней зоне будут иметь вид:

⋅

= sin

⋅

−= cos

jЕ

πωε

⋅

−=

sin

jЕ

πωε

. (5.6)

Полученные выражения соответствуют закону Био-Савара для

магнитного поля и полю электрического диполя в электростатике.

В дальней зоне (зоне излучения, либо волновой зоне) волновым

характером поля (запаздыванием) уже пренебрегать нельзя, однако можно

пренебречь всеми членами, которые убывают быстрее, нежели 1/r. Тогда

выражения для составляющих поля излучения приобретают вид:

НН

= ϕ

= Θ

⋅

−

sin

jkr

lIk

(5.7)

sin

ΘΘ

⋅

=Θ=

−

jkr

lIk

jЕЕ

πωε

(5.8)

Составляющей поля излучения диполя Е

в дальней зоне обычно

пренебрегают в виду ее малости.

Из 5.7-5.8 следует, что, как и в плоской волне, в дальней зоне поля

излучения диполя векторы электрического и магнитного поля взаимно

перпендикулярны. Кроме того, отношение

Ζ===

ωε

(5.9)

представляет собой волновое сопротивление среды.

В промежуточной зоне при расчетах поля излучения диполя никакими

слагаемыми в выражениях 5.3-5.5 пренебрегать нельзя!

Рассмотренные выше особенности относятся лишь к математическим

аспектам описания поля излучения диполя. С физической точки зрения, на

любом расстоянии от диполя присутствуют все три составляющие поля

излучения, и речь может идти лишь о соотношении их амплитуд.

Энергетические характеристики электрического диполя.

Энергетические характеристики электрического диполя, то есть

излучение им электромагнитной энергии в пространство, определяются

средним за период значением вектора Пойнтинга. В общем случае выражение

для среднего за период значения вектора Пойнтинга имеет вид:

]Re[

HEП

ср

&&&

×= , (5.10)

где Re – вещественная часть комплексного числа;

∗

)

- символ комплексно сопряженного числа.

Для составляющих поля излучения 5.3-5.5 среднее значение вектора

Пойнтинга в соответствии с 5.10 описывается выражением:

rППП

rср

+Θ=

. (5.11)

Т.о. вектор Пойнтинга имеет две составляющие – меридиональную П

радиальную П

. После подстановки в 5.11 соответствующих значений Е и Н

можно видеть, что среднее значение меридиональной составляющей равно

нулю, т.е. перенос энергии в меридиональной плоскости отсутствует и здесь

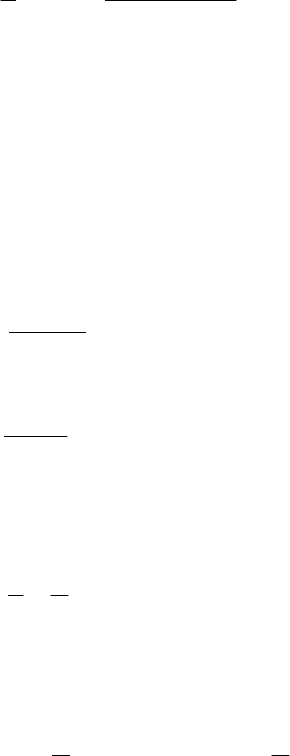
имеет место только пульсация потока мощности, причем с двойной частотой.

Такую мощность принято называть реактивной. Вблизи диполя эта мощность

имеет большую величину, но с увеличением расстояния очень быстро убывает.

Радиальная составляющая вектора Пойнтинга состоит из двух частей –

реактивной, имеющей тот же порядок величины, что и меридиональная часть

мощности, и так же быстро (пропорционально пятой степени расстояния)

убывающая по мере удаления от диполя, и активной, убывающей

пропорционально второй степени расстояния. Выражение для активной

мощности, которая собственно и является мощностью, излучаемой диполем в

пространство имеет вид:

2223

sin

lIк

ПП

ωεπ

. (5.12)

Т.о. в поле излучения диполя существует энергетический поток,

убывающий пропорционально второй степени расстояния, при этом функция

направленности по мощности пропорциональна sin

Θ и ее графическое

представление – диаграмма направленности будет уже, чем диаграмма

направленности по полю, рассмотренная выше.

Если проинтегрировать 5.12 по площади сферы, окружающей диполь, то

можно вычислить полную мощность излучения диполя. Значение этого

интеграла будет равно:

изл

lIк

πωε

223

. (5.13)

Мощность излучения можно представить также в виде:

изл

=Ρ (5.14)

где R

изл

– сопротивление излучения диполя.

Приравняв между собой 5.13 и 5.14, можно получить выражение для

сопротивления излучения:

cизл

)(

= . (5.15)

Здесь Z

– волновое сопротивление среды, в которой расположен

диполь.

Для свободного пространства Z

= 120π. В этом случае:

)(790

изл

= , .)(395

изл

= (5.16)

5.2 Излучение элементарного магнитного диполя

Элементарный магнитный диполь - виток провода, по которому

протекает переменный электрический ток. Длина витка должна быть много

меньше длины волны тока, протекающего по нему, что позволяет считать

амплитуду тока вдоль витка постоянной. Если при этом потребовать, чтобы

расстояние до точки наблюдения было много больше размеров витка, то поле

излучения элементарного магнитного диполя в этой точке с использованием

принципа перестановочной двойственности уравнений Максвелла может быть

записано в виде:

,sin)

(

Θ+−==

−

jЕЕ

jkr

ωϕ

(5.17)

Θ+=

HrHH

где -

Θ−+=

Θ+=

−

sin)

(

,cos)

(

jkr

. (5.18)

В выражениях 5.17-5.18 S - площадь витка с током. Остальные обозначения

аналогичны, использованным ранее обозначениям.

Структура поля элементарного магнитного диполя аналогична

структуре поля элементарного электрического диполя за исключением того,

что векторы напряженности магнитного и электрического поля меняются

местами. Зависимость поля излучения элементарного магнитного диполя от

расстояния до точки наблюдения и угловых координат точно такая же, как и

для электрического диполя. Средний поток мощности в дальней зоне имеет

только одну радиальную составляющую.

Характерной особенностью магнитного диполя является то, что при

одинаковой длине провода с электрическим диполем, его сопротивление

излучения оказывается меньшим, и, следовательно, меньше его излучательная

способность. Так при l ≅ 0.1λ R

изл. эл

/ R

изл. м

≅ 400, поэтому в технике гораздо

чаще применяют разомкнутые системы.

Особенности излучения электромагнитной энергии элементом Гюйгенса

в данном разделе рассматриваться не будут. С ними можно познакомиться в

курсе Устройства СВЧ и Антенны.

Вопросы для самопроверки

1.Какова цель введения понятия элементарного излучателя?

2.Как формулируется задача излучения электромагнитных волн элементарным

излучателем?

3.Какой метод решения используется для расчета излучения элементарного

электрического диполя?

4.Назовите характерные зоны пространства и критерии разделения, в которых принято

рассматривать поле излучения.

5.Охарактеризуйте энергетические свойства поля, излученного элементарным излучателем.

6.Какие характеристики свойственны элементарному излучателю как антенне?

7.Какие модели используются для описания элементарного магнитного излучателя?

8.Сравните излучательную способность элементарных электрического и магнитного

излучателей.

9.Какой вид имеет диаграмма направленности элемента Гюйгенса?

6.Направляющие системы и направляемые волны

6.1 Общие понятия и определения

6.1.1 Классификация линий передачи

Различают свободные и направляемые электромагнитные волны.

Свободными называются электромагнитные волны, распространяющиеся в

неограниченном пространстве. Направляемыми называются электромагнитные

волны, распространяющиеся вдоль линий передачи.

Линией передачи называют устройство, ограничивающее область

распространения электромагнитных волн и обеспечивающее движение потока

энергии электромагнитной волны в заданном направлении. Линии передачи

могут быть регулярными и нерегулярными, однородными и неоднородными.

Регулярной называют линию передачи, у которой поперечное сечение и

электрофизические свойства заполняющих ее сред являются неизменными

вдоль всей линии. Нерегулярной называют линию передачи, у которой

нарушено хотя бы одно условие регулярности.

Однородной называют линию передачи, заполненную однородной

средой. Неоднородной – линию передачи, заполненную неоднородной средой.

В зависимости от наличия или отсутствия в конструкции линии

передачи замкнутого проводящего экрана, отделяющего область пространства,

в которой распространяется направляемая волна, от окружающей среды,

различают волноводы и открытые линии передачи. Волноводами называются

линии передачи, в поперечном сечении которых имеется один или несколько

замкнутых проводящих контуров, охватывающих область распространения

направляемых волн. В поперечном сечении открытых линий передачи таких

контуров нет.

Геометрической характеристикой поперечного сечения линии передачи,

определяющей количество изолированных проводящих поверхностей,

входящих в состав ее конструкции, является «порядок связности» линии

передачи. Различают односвязные, двухсвязные, многосвязные линии и линии

передачи нулевой связности.

6.1.2 Некоторые виды линий передачи.

На рис.6.1 приведены эскизы поперечных сечений некоторых видов

линий передачи:

а – двухпроводная линия передачи (двухсвязная открытая линия

передачи);

б – коаксиальный волновод (двухсвязный волновод с соосными

внешним и внутренним проводниками);

в – микрополосковая линия передачи (двухсвязная открытая

неоднородная линия передачи).

г – прямоугольный волновод (односвязный волновод, имеющий

прямоугольное поперечное сечение);

д – круглый волновод (односвязный волновод, имеющий круглое

поперечное сечение);

е – диэлектрическая линия передачи (открытая линия передачи нулевой

связности).

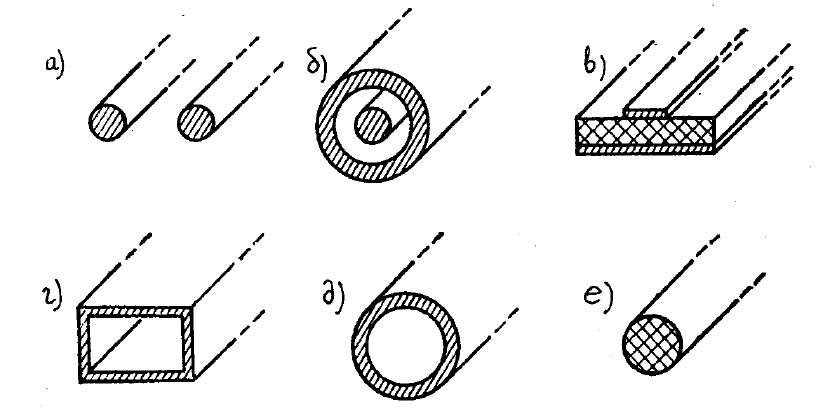
Рис. 6.1. Некоторые виды линий передачи ( а - двухпроводная линия

передачи,

б – коаксиальный волновод, в – микрополосковая линия передачи, г –

прямоугольный волновод, д – круглый волновод, е – диэлектрическая линия

передачи ).

6.1.3 Классификация электромагнитных волн, распространяющихся

в линиях передачи

В зависимости от вида линий передачи в них могут распространяться

электромагнитные волны четырех классов:

• поперечные или Т-волны (старое название и обозначение -

поперечно – электромагнитные или ТЕМ-волны);

• электрические или Е-волны (старое название и обозначение -

поперечно – магнитные или ТМ-волны);

• магнитные или Н-волны (старое название и обозначение -

поперечно – электрические или ТЕ-волны);

• гибридные волны.

Разделение волн, распространяющихся вдоль линий передачи, на

указанные классы производится относительно продольной (направленной вдоль

линии передачи) пространственной координаты z. По отношения к этой

координате в Т-волнах векторы Е и Н имеют только поперечные

(перпендикулярные оси 0z) составляющие; в Е-волнах вектор Е имеет

поперечную и продольную составляющие, а вектор Н – только поперечную; в

Н-волнах вектор Н имеет поперечную и продольную составляющие, а вектор

Е - только поперечную; в гибридных волнах оба вектора (Е и Н ) имеют и

продольные и поперечные составляющие. Заметим, что в линиях передачи ось

0z совпадает с направлением движения распространяющихся вдоль этих линий

электромагнитных волн.

Т-волны могут существовать только в двухсвязных или многосвязных

линиях передачи (причем как в открытых линиях, так и в волноводах).