Лекции - Электродинамика и распространение радиоволн (тексты лекций)

Подождите немного. Документ загружается.

электродинамическим задачам. Их можно классифицировать как задачи

анализа и задачи синтеза.

Задачи анализа предполагают исследование полей в пространстве, или

каких либо технических характеристик устройства при известном

распределении источников.

Задачи синтеза предполагают создание определенного распределения

источников, либо создание технического устройства, обеспечивающего

заданное распределение полей в пространстве, либо заданные технические

характеристики. Задачи синтеза являются существенно более сложными,

зачастую реализация их решения технически невозможна, и в данном курсе

они рассматриваться не будут.

Задачи анализа можно разделить на внутренние и внешние.

Внутренняя задача формулируется следующим образом: необходимо

отыскать решение уравнений Максвелла или соответствующих им волновых

уравнений в области V, ограниченной поверхностью S, удовлетворяющее на

этой поверхности граничным условиям. При решении внутренних задач

различают два решения – отыскание собственных функций, что соответствует

решению однородных волновых уравнений, и отыскание полей заданных

источников, соответствующих решению неоднородных волновых уравнений.

Примером подобных задач является задача отыскания полей в объемном

резонаторе. Решение однородного волнового уравнения позволяет найти

свободные колебания резонатора, а решение неоднородного уравнения –

вынужденные колебания. Доказано, что решение обеих задач существует и при

выполнении граничных и начальных условий является единственным.

Среди внешних задач наиболее простой является задача излучения

заданной системы источников в однородном безграничном пространстве. Она

формулируется следующим образом: в свободном безграничном пространстве

необходимо найти решение неоднородного волнового уравнения,

удовлетворяющее условию излучения на бесконечности (которое является

эквивалентом граничных условий для внутренних задач). Доказано, что

решение задачи существует и является единственным.

Другим, несколько более сложным, примером внешней задачи

электродинамики является задача излучения заданной системы источников в

безграничное, неоднородное пространство. Задача формулируется также как и

предыдущая, только предполагается дополнительно, что функция,

описывающая распределение параметров среды, является непрерывной и имеет

непрерывные первые производные.

3.2 Строгие методы решения

Все методы решения задач электродинамики можно разделить на

строгие и приближенные. Если результат решения задачи любым из строгих

методов является одинаковым, то результаты решения приближенными

методами, различаются, и степень их строгости зависит от характера

использованных приближений.

К числу строгих методов решения задач электродинамики относят:

-метод разделения переменных (метод Фурье);

-метод запаздывающих потенциалов;

-метод скалярного и векторного интеграла Кирхгофа.

Метод разделения переменных применим в любой ортогональной

системе координат, выбранной таким образом, чтобы граничные поверхности

тела (либо области пространства) совпадали или были параллельными

координатным поверхностям. Решение однородного волнового уравнения в

диэлектрической среде (уравнения Даламбера) методом разделения

переменных в прямоугольной системе координат представляется в виде:

С = С

ехр(–j(к

х +к

у +к

z)) + С

ехр(j(к

х +к

у +к

z)). (3.1)

Здесь: С – любая из проекций любого вектора электромагнитного поля

на координатные оси;

,С

- постоянные интегрирования;

,к

у,

- проекции волнового числа (постоянной распространения) на

координатные оси.

В (3.1) первое слагаемое описывает уходящую волну, а второе –

приходящую. Исходя из физической специфики задачи, одно из них (чаще

второе) отбрасывается.

Более подробно данный метод решения на конкретном примере плоской

волны рассматривается в следующем разделе письменных лекций.

Решение волнового уравнения методом запаздывающих потенциалов

основано на том физическом представлении, что электромагнитное

возмущение, созданное источниками, сосредоточенными в некоторой области

пространства, достигает точки наблюдения не мгновенно, а с некоторым

запаздыванием, величина которого определяется скоростью распространения

возмущения v и расстоянием до точки наблюдения r. Это означает, что

интересующая нас характеристика электромагнитного поля в точке

наблюдения в настоящий момент времени t обязана своим существованием

вариациям источника поля в предшествующий (более ранний) момент времени

– (t -

). Кроме того, амплитуда рассматриваемой характеристики поля, в

соответствии с условиями излучения, физический смысл которых состоит в

том, что на бесконечном удалении от источника амплитуда поля должна

стремиться к нулю, убывает пропорционально первой степени расстояния. Т.о.

решение волнового уравнения методом запаздывающих потенциалов будет

иметь вид:

- для вектора напряженности магнитного поля, когда источники

распределены в объеме V,

∫

−

ст

trot

)(

, (3.2)

- для скалярного потенциала при тех же условиях

∫

−

ст

)(

πε

. (3.3)

Аналогичным образом могут быть записаны решения волновых

уравнений и для других характеристик электромагнитного поля,

рассмотренных ранее. В тех случаях, когда источники электромагнитного поля

распределены не в объеме, а на поверхности или линейно, интегрирование

распространяется на соответствующие поверхности или линии при сохранении

общего вида решения.

Для гармонических полей эти решения принимают вид (на примере

записи решения для векторного потенциала при распределении источников по

поверхности):

∫

−

ст

эа

jkr

)exp(

. (3.4)

В выражениях (3.2, 3.3, 3.4) r – расстояние от каждой точки

рассматриваемого объема (поверхности, кривой), где распределены источники,

до точки наблюдения;

−

ст

ρδ

, функции координат, описывающие распределение источников

(токов, зарядов) внутри рассматриваемого объема (на поверхности, по линии).

Метод решения волновых уравнений с помощью скалярного либо

векторного интегралов Кирхгофа в данном разделе рассматриваться не будет,

поскольку применение их в качестве строгих методов весьма ограничено и

гораздо чаще (особенно это относится к скалярному интегралу Кирхгофа) они

используются как методы приближенные.

3.3 Приближенные методы решения

Говоря о приближенных методах решения задач электродинамики,

прежде всего нужно определить области их применения. В зависимости от

соотношения геометрических размеров области пространства L, где требуется

найти решение, и длины электромагнитной волны λ принято рассматривать три

зоны:

-квазистационарную -

<<1;

-резонансную - 1≈

;

-квазиоптическую -

>>1.

В квазистационарной области решение задач базируется на методах

электро- и магнитостатики. В резонансной – на строгих методах.

Приближенные методы используются в квазиоптической области. К числу

приближенных методов решения задач электродинамики относят методы:

геометрической оптики, волновой (физической) оптики, краевых волн,

геометрической теории дифракции. В перечисленной последовательности

приближенные методы позволяют получить более точное решение,

стремящееся к строгому решению.

Метод геометрической оптики является предельным при решении

волновой задачи, когда длина волны λ стремится к нулю. Это означает, что

здесь не учитывается волновой характер поля. Этот метод применим при

определении электромагнитного поля (чаще всего при решении задач на

отражение электромагнитных волн) когда размеры отражающего тела и

минимальный радиус кривизны его поверхности велики по сравнению с

длиной волны. Кроме того, необходимо, чтобы источник поля находился на

достаточно большом расстоянии от поверхности тела.

Основные положения метода геометрической оптики состоят в том, что:

электромагнитная энергия распространяется внутри лучевых трубок; поток

энергии внутри каждой лучевой трубки постоянен; амплитуды векторов поля в

каждой точке пространства определяются из постоянства потока энергии

внутри лучевой трубки; фазы электромагнитных колебаний в каждой точке

пространства определяются длиной пути от источника до точки наблюдения и

изменяются вдоль луча линейно; если через точку наблюдения проходит

несколько лучевых трубок, то результирующее поле определяется как

геометрическая сумма полей всех составляющих.

Следует иметь в виду, что понятие лучевой трубки применимо, когда

амплитуды векторов поля и параметры среды мало изменяются на расстоянии

длины волны, что в однородной среде лучи являются прямыми линиями, а в

неоднородной – плавными кривыми, что перераспределение энергии между

соседними лучевыми трубками отсутствует и векторы

и Η

перпендикулярны

лучу.

В геометрической оптике предполагается, что поле в точке наблюдения

определяется значениями его векторов в тех точках отражающей поверхности

или волнового фронта поля источника, из которых лучи приходят в данную

точку. Иными словами, метод геометрической оптики дает решение только в

«освещенной» области пространства. В тени он не работает!

Метод волновой оптики (физической оптики), в отличие от

предыдущего, учитывает волновой характер электромагнитного поля и

базируется в соответствии с принципом Гюйгенса на представлении поля

точечного источника в виде волновой функции

Ψ = Ψ

exp

jω(τ -r/v)

/r,

где Ψ- любая составляющая вектора поля;

ω - круговая частота;

r - расстояние до точки наблюдения;

v - скорость волнового процесса.

Этот метод применим при тех же ограничениях, что и метод

геометрической оптики, т.е. для больших, гладких тел, когда точка наблюдения

находится на достаточном расстоянии от источника. Однако метод волновой

оптики позволяет определять электромагнитное поле и в области

геометрической тени (иными словами при использовании этого метода области

тени за объектом не существует, что реально и наблюдается за счет эффекта

дифракции).

Амплитуда поля в точке наблюдения определяется вкладом всех

участков волнового фронта поля источника, как геометрическая сумма

колебаний с учетом амплитуды и фазы каждого в зависимости от расстояния до

точки наблюдения. Строгая математическая формулировка метода волновой

оптики с точностью до постоянного фазового множителя exp(jπ/2) совпадает с

формулой скалярного интеграла Кирхгофа. В то же время метод волновой

оптики смыкается с методом геометрической оптики в том отношении, что

значения волновой функции реально могут быть заданы строго только в

пределах освещенного (полем источника) участка волнового фронта, а в

теневой области полагаются равными нулю. Это же обстоятельство не

позволяет в интеграле Кирхгофа задать строго значения всех подинтегральных

функций и использовать этот интеграл в качестве строгого решения задач

электродинамики.

Метод краевых волн является развитием метода волновой оптики

применительно к телам, поверхность которых имеет изломы, ребра и т.д. Он

используется при тех же ограничениях, что и предыдущий метод, только

позволяет несколько ослабить требования по соотношению размеров тела,

радиуса кривизны его поверхности и расстояния до точки наблюдения и длины

электромагнитной волны.

Суть метода краевых волн состоит в том, что в отличие от предыдущих

методов, где на теневой части тела, либо волнового фронта источника поле

полагалось равным нулю, поле источника на теневой поверхности вблизи краев

тела (ребер, изломов) отлично от нуля. Это отличие связано с появлением

вблизи границ тела дополнительной (возмущенной) составляющей

поверхностного тока, вызванной влиянием края тела. Эта составляющая

отличается от нуля на расстояниях порядка длины волны от края тела, носит

характер краевой волны и может быть определена как результат строгого

решения задачи дифракции электромагнитной волны на клине.

Т.о. более точное задание волновой функции на фронте волны

источника, либо более точное задание подинтегральных функций в интеграле

Кирхгофа позволяет получить более строгое решение электродинамической

задачи.

Метод геометрической теории дифракции представляет собой развитие

метода геометрической оптики применительно к решению задач дифракции

электромагнитных волн на больших (по отношению к длине волны) телах

сложной геометрической формы. Он также базируется на предположении, что

энергия распространяется внутри лучевых трубок с теми же особенностями,

что и в методе геометрической оптики, однако в отличие от метода

геометрической оптики, кроме падающих, отраженных и преломленных лучей

вводятся в рассмотрение дифрагированные лучи. Для определения амплитуды

поля в каждой точке пространства необходимо найти все лучи, проходящие

через эту точку, вычислить поля, соответствующие каждому лучу и

просуммировать их. При определении поля дифрагированного луча

предполагается, что оно пропорционально в точке дифракции (точке

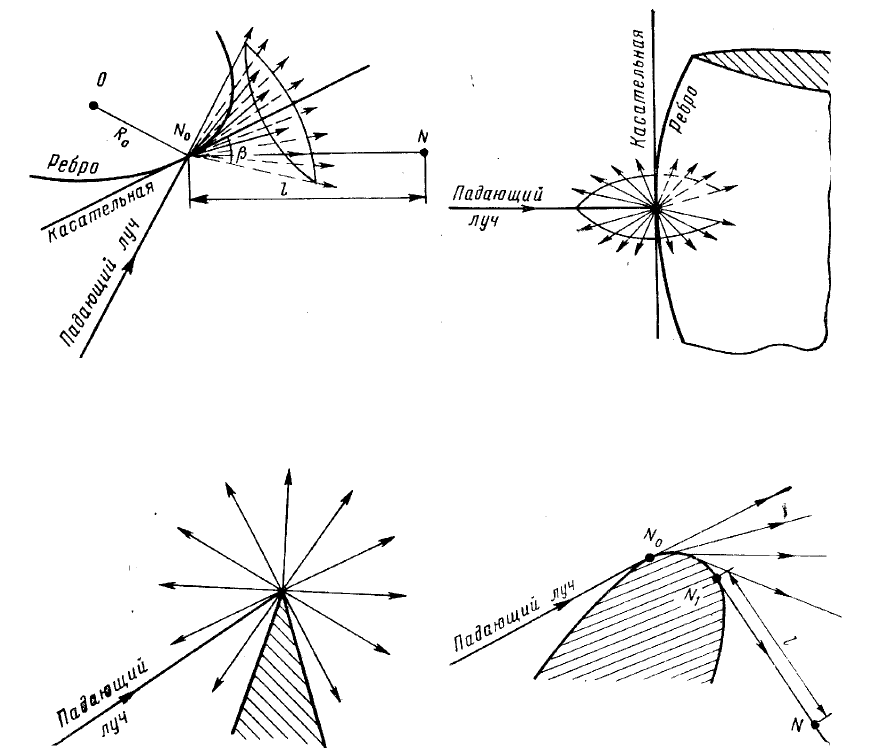
соприкосновения падающего луча с краем тела) полю падающего луча. При

этом коэффициент пропорциональности называют коэффициентом дифракции.

Предполагается также, что фаза дифрагированного луча меняется линейно

вдоль луча, а характер изменения амплитуды устанавливается на основе

постоянства потока энергии внутри лучевой трубки. Характерные картины

распределения в пространстве дифрагированных лучей приведены ниже на рис.

3.1-3.4.

Рис.3.1 Рис.3.2

Рис.3.3 Рис.3.4

Метод геометрической теории дифракции позволяет получить

результаты, при решении задач дифракции на телах сложной конфигурации,

которые хорошо согласуются с результатами строгого решения и результатами

экспериментальных исследований. Однако применение этого метода

достаточно затруднительно, когда необходимо найти поле в области каустики

(область куда приходит очень большое число лучей – например фокальная

область). В этих случаях применяются специальные методы, которые здесь не

рассматриваются.

Вопросы для самопроверки

1. Как формулируются внутренние и внешние задачи электродинамики?

2. В чем состоит роль условия излучения при решении внешних задач?

3.Как формулируется теорема единственности решения задач электродинамики?

4.При каких условиях справедлив принцип суперпозиции решений?

5.Для каких сред выполняется теорема взаимности и в чем заключается ее сущность?

6. Какова роль теоремы эквивалентности при решении внешних задач

электродинамики?

7.Что лежит в основе решения задач методом запаздывающих потенциалов?

8. При каких условиях метод Кирхгофа может рассматриваться как строгий метод

решения?

9. Сформулируйте условия применимости методов геометрической и волновой оптики.

10. В чем состоит сущность методов краевых волн и геометрической теории

дифракции?

4. Плоские волны

Всякое распространяющееся в пространстве электромагнитное поле

принято называть электромагнитной волной. Если векторы Е и Н

электромагнитной волны изменяются во времени по гармоническому закону,

то она называется гармонической. В настоящем разделе мы будем

рассматривать только гармонические электромагнитные волны.

В каждой точке пространства в фиксированный момент времени

составляющие векторов поля гармонической волны имеют определенные

амплитуды и фазы. Поверхность, во всех точках которой составляющие

векторов поля изменяются синфазно, называется поверхностью равных фаз или

фазовым фронтом. Поверхность, во всех точках которой составляющие

векторов поля имеют равные амплитуды, называется поверхностью равных

амплитуд.

Электромагнитные волны принято классифицировать по виду

поверхности равных фаз. Различают плоские, сферические, цилиндрические и

другие волны. Простейшими из них являются плоские волны. Плоской

называется волна, у которой поверхности равных фаз – параллельные

плоскости. Если поверхности равных амплитуд плоской волны совпадают с

поверхностями равных фаз, то такая волна называется однородной. В

однородной плоской волне векторыЕ иН изменяются в пространстве только

вдоль одного направления, перпендикулярного фазовому фронту этой волны и

совпадающего с направлением ее распространения.

Плоская волна, в которой поверхности равных амплитуд не плоскости

или плоскости, не совпадающие с поверхностями равных фаз, называется

неоднородной. В настоящем разделе мы будем рассматривать только

однородные плоские волны.

Источников, возбуждающих плоские волны, в природе не существует,

соответственно физически не существует и плоских волн. Все реальные

излучатели на расстояниях, значительно превышающих их линейные размеры,

создают сферические волны. Однако, при определенных допущениях

ограниченный участок сферы можно считать плоским. Следовательно,

электромагнитную волну, возбуждаемую реальным излучателем, в

ограниченной области пространства, находящейся на достаточном удалении от

этого излучателя, можно рассматривать как плоскую. Кроме того, любую

электромагнитную волну можно представить в виде суммы элементарных

плоских волн, что в ряде случаев существенно упрощает анализ. Строго говоря,

плоская волна – некая математическая абстракция!

4.1 Решение уравнений электродинамики для плоской волны

Получим решение системы уравнений Максвелла, соответствующее

гармонической, однородной плоской волне, распространяющейся в однородной

среде с параметрами ε

, µ

, γ. Будем считать, что сторонние токи и сторонние

заряды в рассматриваемой области пространства отсутствуют. При принятых

допущениях первое и второе уравнения Максвелла в комплексной форме будут

выглядеть следующим образом:

rot

Η = jω

Ε ; rot

= - jω µ

, (4.1)

где

= ε

– j γ / ω - комплексная диэлектрическая проницаемость.

Совместим ось 0z декартовой системы координат с направлением,

вдоль которого изменяются векторы Е и Н, т.е. с направлением

распространения волны. Тогда частные производные этих векторов по

пространственным переменным x и y будут равны нулю. В этом случае

продольные (вдоль оси 0z) составляющие векторов rot

Η и rot

Ε оказываются

равными нулю, а значит (см.(4.1)) окажутся равными нулю и продольные

составляющие векторов Е и Н:

rot

Η = ∂

/∂x - ∂

/∂y = jω

= 0

rot

Ε = ∂

/∂x - ∂

/∂y = - jωµ

= 0

Так как составляющие векторовЕ иН плоской однородной волны,

параллельные направлению ее распространения, равны нулю (Е

= Н

= 0), то

волна является поперечной – т.е. волной, векторыЕ иН которой целиком

лежат в плоскости ее фазового фронта. В принятой системе координат

отличными от нуля могут быть только составляющие Е

этих векторов.

Поперечные волны обозначаются символом Т, принятым, для краткости,

вместо применявшегося ранее символа ТЕМ (transverse electromagnetic).

От уравнений (4.1) можно легко перейти к волновому уравнению для

комплексной амплитуды вектораЕ, которое в рассматриваемом случае (δ

ст

= 0) будет однородным:

∇

Ε +

= 0, (4.2)

где

- комплексное волновое число, которое может быть найдено

следующим образом (см. 2.14, 2.15):

= ω

- jωγµ

. (4.3)

Будем пока рассматривать плоскую волну, в которой векторы Е иН в

каждой точке пространства изменяются во времени вдоль одного направления

(линейно поляризованная волна). Совместив ось 0х с направлением, вдоль

которого изменяется векторЕ, будем иметь Е

= 0. В этом случае векторЕ

будет иметь только одну составляющую Е

Ε =

x

При этом трехмерное волновое уравнение в частных производных (4.2)

переходит в одномерное волновое уравнение относительно составляющей

представляющее собой обыкновенное однородное дифференциальное

уравнение второго порядка с постоянными коэффициентами:

/dz

+ k

= 0. (4.4)

Общее решение такого уравнения хорошо известно и может быть

представлено в следующем виде (сравни с 3.1):

пад

exp(-j z) +

отр

exp(j z), (4.5)

где комплексные в общем случае величины

пад

отр

являются

постоянными интегрирования.

Положим

пад

= Е

пад

exp(jψ

пад

);

отр

= Е

отр

exp(jψ

отр

). (4.6)

Имея решение для вектора Е, значение вектора Н можно найти из

второго уравнения Максвелла:

Η = - rot

/jωµ

Подставив сюда

Ε =

x

, получим:

Η = - (1/jωµ

/dzy

y

откуда, принимая во внимание (4.5) и (4.3), находим

= ( /ωµ

)(

пад

exp(-j z) -

отр

exp(j z)) =

аа

µε

(

пад

exp(-j z) -

отр

exp(j z)). (4.7)

Проведенные вычисления показывают, что вектор Н имеет только одну

составляющую, параллельную оси 0y, и, следовательно, векторы Е иН в

плоской однородной волне взаимно перпендикулярны (ортогональны).

Введя в рассмотрение новую величину

εµ

, Ом, (4.8)

запишем общее решение системы уравнений Максвелла для однородной

линейно поляризованной плоской волны в окончательном виде:

Ε =

x

= (

пад

exp(-j z)+

отр

exp(j z))x

пад

отр

; (4.9)

Η =

у

= (1/ Ζ

)(

пад

exp(-j k z)-

отр

exp(j z))у

пад

отр

где символами

пад

обозначено первое частное решение,

а символами

отр

– второе.

Величину

, имеющую размерность сопротивления, называют

характеристическим сопротивлением плоской волны. Согласно (4.9)

характеристическое сопротивление равно отношению комплексных амплитуд

векторов напряженности электрического и магнитного полей в падающей и

отраженной волнах соответственно:

пад

/ Η

пад

= -

отр

. (4.10)

4.2 Распространение плоских волн в различных средах

Плоские волны в идеальном диэлектрике. В случае идеального

диэлектрика (γ = 0) характеристическое сопротивление Z

и волновое число k

являются вещественными величинами. Учитывая это, перейдем от

комплексных амплитуд к мгновеным значениям векторовЕ и Н. Для этого

умножим выражения (4.9) на exp(jωt) и возьмем от полученных произведений

вещественные части. В результате, с учетом равенства (4.6), будем иметь:

Е(z,t) = Е

пад

(z,t) + Е

отр

(z,t) = Е

пад

cos(ωt–kz+ψ

пад

+Е

отр

cos(ωt+kz+ψ

отр

);

(4.11)

Н(z,t) = Н

пад

(z,t) + Н

отр

(z,t) = (1/Z

)(Е

пад

cos(ωt–kz+ψ

пад

) -

-Е

отр

cos(ωt+kz+ψ

отр

)),

где Z

аа

εµ

/ .

Убедимся, что первые слагаемые в этих выражениях определяют волну,

распространяющуюся в положительном направлении оси 0z. Действительно,

если время t будет возрастать, то для того, чтобы значение косинуса было

постоянным, необходимо, чтобы его аргумент (фаза волны) также оставался

постоянным:

ωt–kz+ψ

пад

= const. (4.12)

Условие (4.12) может быть выполнено только в том случае, если вместе

с t растет и координата z. Это означает, что фиксированные значения Е

пад

(соответствующие фиксированным значениям фазы) с течением времени

перемещаются в положительном направлении оси 0z. Cкорость этого

перемещения может быть найдена из уравнения (4.12), представляющего собой

уравнение поверхности равной фазы. Дифференцируя его по времени,

получаем:

ω – k(dz/dt) = 0,

откуда скорость перемещения поверхности равных фаз V будет равна:

V = dz/dt = ω/k. (4.13)

Эту скорость называют фазовой скоростью плоской однородной волны.

Для идеального диэлектрика k = ω

аа

µε

и фазовая скорость в нем зависит

только от параметров среды :

V = 1/

аа

µε

(4.14)

Волну, распространяющуюся в положительном направлении оси 0z,

называют падающей. Рассуждая совершенно аналогично, придем к выводу, что

вторые слагаемые в формулах (4.11) определяют волну, распространяющуюся в