Лекции - Электродинамика и распространение радиоволн (тексты лекций)
Подождите немного. Документ загружается.

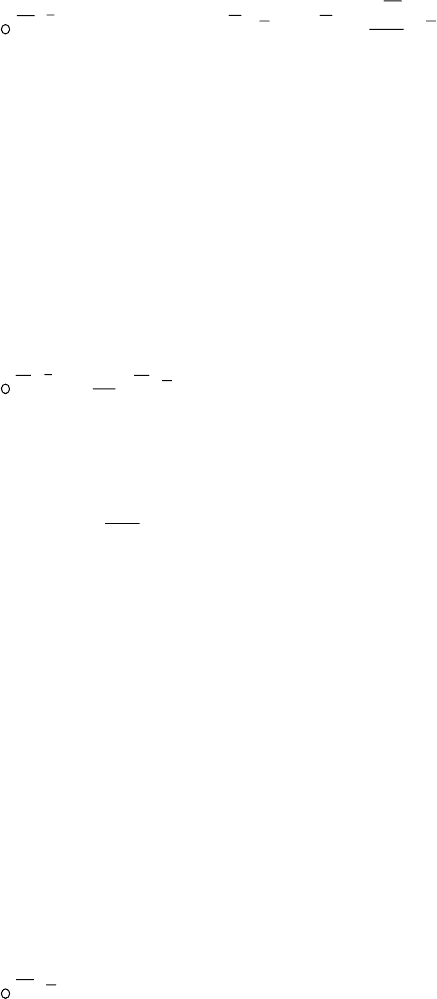
величину и знак. Электрическая цепь является замкнутой, то есть ток
проводимости замыкается током, названным Максвеллом током смещения.
С учетом (1.21) и (1.22) первое уравнение Максвелла записывается в
виде:
∫∫∫
∂
∂
+==+==
LSS
прпсмпрп
sd
t
D
sdiiildH )(
δδ
. (1.23)
Т.о. физический смысл первого уравнения Максвелла состоит в том, что
магнитное поле в некоторой области пространства связано не только с токами
проводимости, протекающими в этой области, но и с изменением
электрического поля во времени в этой области (токами смещения).
b. Второе уравнение.
Циркуляция вектора напряженности электрического поля по
замкнутому контуру равна скорости изменения магнитного потока,
пронизывающего этот контур. Математически это определение записывается
следующим образом:
∫∫
∂
∂
−=
LS
sdB
t
ldE
. (1.24)
Это уравнение совпадает с законом электромагнитной индукции
Фарадея, который в свернутом виде может быть записан так:
ЭДС = -
t
Ф
∂
∂
. До Максвелла этот закон рассматривался применительно к
реальным контурам, образованным проводниками. Максвелл же использовал
этот закон применительно к любому (выделенному умозрительно) контуру в
пространстве. Знак минус в обоих случаях означает то, что наведенная в
контуре ЭДС создает собственный магнитный поток, препятствующий
изменению внешнего.
Физический смысл второго уравнения Максвелла состоит в том, что
электрическое поле в некоторой области пространства связано с изменением
магнитного поля во времени в этой области.
c. Третье уравнение.
Поток вектора электрической индукции через замкнутую поверхность
равен сумме зарядов, заключенных внутри этой поверхности. В соответствии с
теоремой Гаусса:
dvqsdD
VS
∫
∑
∫
==
ρ
. (1.25)
Здесь: q - полный электрический заряд внутри поверхности S;
V- объем, ограниченный поверхностью S;
ρ- объемная плотность электрического заряда.
Физический смысл этого уравнения состоит в том, что электрическое
поле в некоторой области пространства связано с электрическим зарядом
внутри этой области. Это уравнение свидетельствует также о том, что
электрическое поле имеет истоки в виде электрических зарядов. Для
положительного заряда силовые линии вектора электрической индукции
11
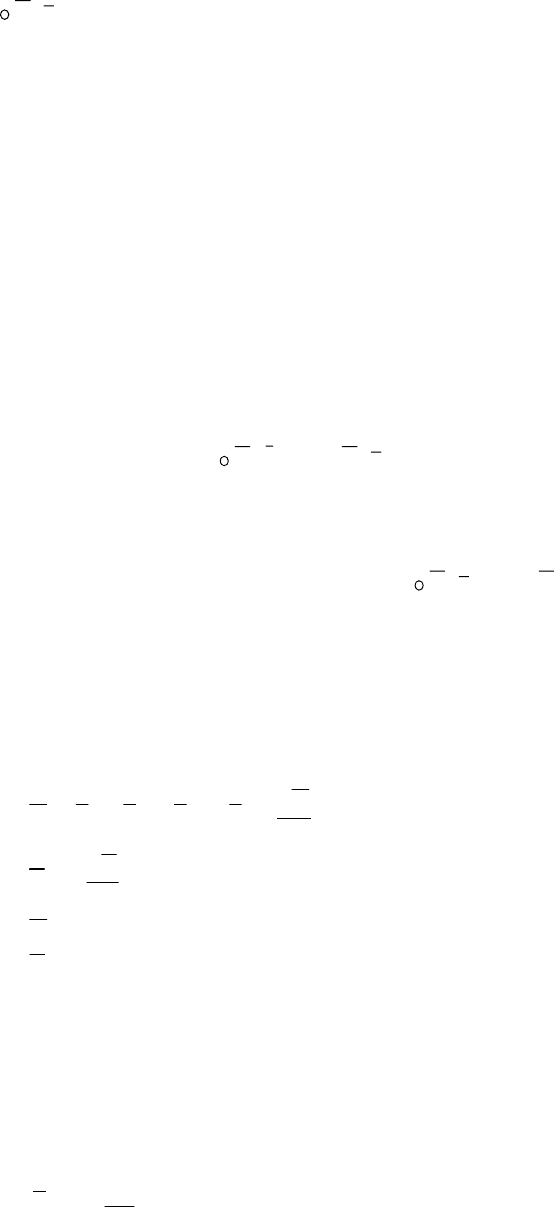
выходят из рассматриваемого объема (исток); для отрицательного заряда –
входят (сток).
d. Четвертое уравнение.
Поток вектора магнитной индукции через замкнутую поверхность равен
нулю (поскольку магнитных зарядов одного знака в природе не обнаружено).
Математически это уравнение записывается так:
∫
=
S
sdB 0
. (1.26)
Физический смысл этого уравнения состоит в том, что магнитное поле в
некоторой области пространства не имеет источников в виде неподвижных
зарядов, т.е. не имеет истоков и стоков и силовые линии вектора магнитной
индукции замкнуты (соленоидальны).
1.7 Уравнения Максвелла в дифференциальной форме
В большинстве практических приложений уравнений Максвелла
требуется связать векторы поля с источниками в конкретной точке
пространства. Для этой цели более удобна иная математическая форма записи
уравнений – дифференциальная.
Переход от интегральной к дифференциальной форме записи уравнений
можно осуществить с помощью известных из векторного анализа теорем
Стокса и Гаусса-Остроградского.
Теорема Стокса:
∫∫
=
LS
sdArotldА - циркуляция вектора по замкнутому
контуру равна потоку ротора этого вектора через поверхность, опирающуюся
на данный контур.
Теорема Гаусса-Остроградского:
∫∫
=
SV
dvAdivsdA - поток вектора через
замкнутую поверхность равен дивергенции (расходимости) этого вектора из
объема, ограниченного данной поверхностью.
Применив первую теорему к первому и второму, а вторую – к третьему
и четвертому уравнениям Максвелла в интегральной форме, можно получить
все четыре уравнения в дифференциальной форме:
t
D
Hrot
прсмпрп
∂
∂
+=+==
δδδδ
;
t
B
Erot
∂
∂
−=
; (1.27)
ρ
=Ddiv ;
0=Bdiv .
Для полной характеристики электромагнитного поля при использовании
уравнений Максвелла в дифференциальной форме необходимо ввести еще
одно уравнение – непрерывности, базирующееся на принципе сохранения
заряда. Вывод этого уравнения основывается на связи тока, вытекающего из
элементарного объема, с уменьшением заряда внутри этого
объема…Уравнение непрерывности имеет вид:
t
div
пр
∂
∂
−=
ρ
δ
. (1.28)
12

1.8 Полная система уравнений Максвелла
а. Сторонние электрические силы
Если ЭМП создается какими либо внешними по отношению к
рассматриваемой области источниками, то последние принято называть
сторонними. В качестве таковых рассматриваются: вектор плотности
стороннего электрического тока
ст
э
δ
, который в единицах СИ имеет
размерность А/м
2
,
и объемная плотность стороннего электрического заряда ρ
э
ст
с размерностью в единицах СИ Кл/м
3
. Эти источники являются заданными и
определяются не теми векторами поля, которые должны быть найдены, а
связаны с известными полями; они (источники) могут иметь любую
физическую природу. С учетом этих источников первое и третье уравнения
Максвелла приобретают вид:
∫∫∫
+
∂
∂
+==++==
LSS
ст
эпрп
ст
смпрп
sd
t
D
sdiiiildH
)(
δδδ
(1.29)
dvqsdD
ст
э
VS
)(
ρρ
+==
∫
∑
∫
, (1.30)
в интегральной форме записи и
ст
эсмпрп
Hrot
δδδδ
++== , (1.31)
ст
э
Ddiv
ρρ
+= (1.32)
- в дифференциальной форме.
Система уравнений Максвелла (1.27) при замене первого и третьего
уравнений на (1.31) и (1.32) носит название полной несимметричной системы.
b. Сторонние магнитные силы
Для целого ряда практических приложений уравнений Максвелла
удобно ввести, по аналогии с электрическими, фиктивные, сторонние
магнитные токи и заряды. Обычно используют: вектор плотности стороннего
магнитного тока
ст
м
δ
, имеющий размерность в единицах СИ В/м
2
, и объемную
плотность стороннего магнитного заряда
с размерностью в СИ- В сек/м
ст
м
ρ
3
.
По аналогии же с электрическими токами и зарядами, для магнитных токов и
зарядов можно записать уравнение непрерывности (смотри 1.28):
t
div
ст
м
ст
м
∂
∂
−=
ρ
δ
. (1.33)
Нужно иметь в виду, что в природе магнитных зарядов одного знака не
существует, однако магнитные диполи могут быть уподоблены диполям
электрическим.
Введение фиктивных магнитных токов и зарядов позволяет записать
второе и четвертое уравнения Максвелла в виде:
∫∫
−
∂
∂
−=
LS
ст
м
sdB
t
ldE )(
δ
, (1.34)
∫
=
S
ст
м
sdB
ρ
- (1.35)
интегральная форма записи и
13

ст
м
B
t
Erot
δ
−
∂
∂
−=
, (1.36)
ст
м
Bdiv
ρ
= - (1.37)
дифференциальная форма.
Система уравнений Максвелла с учетом сторонних сил электрического
и магнитного типов (1.31),(1.32),(1.36),(1.37) носит название полной
симметричной системы.
1.9 Система уравнений Максвелла в комплексной форме.
Известно, что для анализа гармонических электродинамических
процессов, оказывается удобным использовать символический метод
представления исследуемых величин. При этом уравнения Максвелла
существенно упрощаются по форме записи и принимают вид:
ст
эпр
ст
эсмпрп
DjHrot
δωδδδδδ
&
&
&&&&&
&
++=++==
,
ст
м
BjErot
δω
&
&&
−−=
, (1.38)
ст
э
Ddiv
ρρ
&&
&
+=
,
ст
м
Bdiv
ρ
&
&
=
.
Здесь ω – частота гармонического процесса.
В выражениях 1.38, по отношению к исходным уравнениям с временной
зависимостью e
jωt
, выполнена процедура дифференцирования по времени и
проведено сокращение на множитель е
jωt
.
Т.о. при гармонической зависимости от времени в уравнениях
Максвелла операция дифференцирования по времени заменяется умножением
на постоянный множитель jω. Решение задачи может проводиться с
комплексными величинами, а затем мгновенное значение искомого вектора
находится как вещественная часть полученного комплексного числа,
предварительно умноженного на сокращенный множитель.
1.10 Комплексная диэлектрическая проницаемость среды.
Классификация сред по проводимости.
Если в первом уравнении системы 1.38 произвести замену вектора
плотности тока проводимости
δ
пр
и вектора электрической индукции D через
величины, входящие в материальные уравнения 1.18 и 1.19, то оно
перепишется в виде:
ст
эа
ст
эсмпрп
EjEHrot
δωξγδδδδ
&
&&
&&&&
&
++=++==
.
После преобразований в правой части этого уравнения, можно записать:
ст
эап
EjHrot
δξωδ
&
&
&
&
&
+==
, (1.39)
где:
- абсолютная комплексная диэлектрическая
проницаемость;
21 ааа
j
ξξξ
−=
&
ω
γ
ξξξ
==
21
,
ааа
.
14

Введение понятия комплексной диэлектрической проницаемости среды
позволяет не только использовать известные решения уравнений Максвелла,
полученные для диэлектрических сред, в средах полупроводящих и
проводящих, но и провести более строгую классификацию сред по
проводимости. Поскольку вещественная часть диэлектрической проницаемости
характеризует величину плотности токов смещения, а мнимая ее часть – токов
проводимости, то при :
ε
а1
>>ε
а2
среда является диэлектриком,
ε
а1
≅ε
а2
- полупроводником и
ε
а1
<<ε
а2
- проводником.
Так как мнимая часть комплексной диэлектрической проницаемости
зависит от частоты, то понятие проводимости является относительным, т.е.
одна и та же среда на различных частотах электромагнитных колебаний может
проявлять себя различным образом (при этом имеется в виду, что ε
а
и γ
постоянны).
Для полной характеристики радиотехнических материалов (сред)
достаточно задать величину диэлектрической проницаемости ε
а
и тангенс угла
диэлектрических потерь - tqδ.
аа
а
tq
ωξ
γ
ξ
ξ
δ
==
1
2
; (1.40)
)1(
δξξ
jtq
аа
−=
&
. (1.41)
1.11 Теорема Умова-Пойнтинга.
Источники поля (сторонние токи и заряды) сообщают свою энергию
электромагнитному полю, при этом она может преобразовываться в другие
формы (тепловая, химическая…), переноситься в другие области пространства,
запасаться полем. Уравнение баланса в свернутом виде можно записать
следующим образом:
Р
ст
=Р
т
+Р
из
+Р
п
, (1.42)
где: Р
ст
– мощность, выделяемая сторонними источниками;
Р
т
– мощность тепловых потерь;
Р
п
- мощность, запасенная электромагнитным полем;
Р
изл
- мощность, переносимая в другие области пространства.
Доказательство указанной теоремы состоит в том, что на основе первого
и второго уравнений Максвелла в дифференциальной форме со сторонними
источниками в виде плотностей электрического и магнитного токов, путем
математических преобразований получается уравнение, представляющее
дифференциальную форму теоремы Умова-Пойнтинга. Преобразования
заключаются в скалярном умножении всех членов первого и второго
уравнений Максвелла на векторы
НЕ , соответственно, вычитании из первого
полученного уравнения второго, использовании известного соотношения
теории поля
)( HEdivErotHHrotЕ ×−=− и перегруппировке полученных
слагаемых. Последующее интегрирование по некоторой области пространства
V, ограниченной поверхностью S, преобразует это уравнение к виду:
15
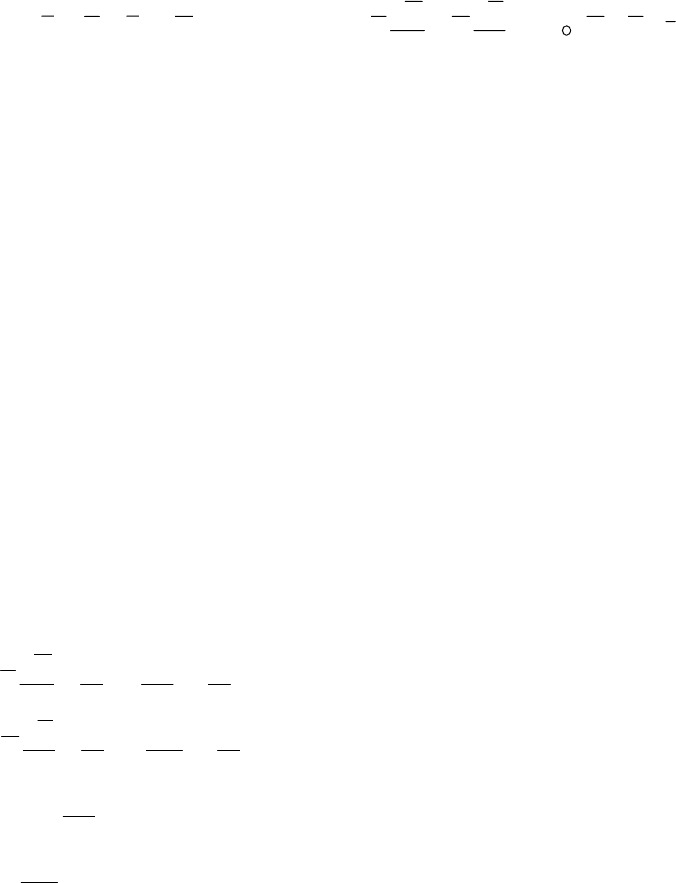
∫∫∫∫
×+
∂
∂
+
∂
∂
+=+−
VVVS
ст
М
ст
Э
sdEHdv
t
B
H
t
D
EdvЕdvНЕ
)()()(
2
γδδ
. (1.43)
Здесь последнее слагаемое в правой части получено при использовании
теоремы Гаусса-Остроградского.
Выражение (1.43) является математической записью теоремы Умова-
Пойнтинга. Сопоставление данного уравнения с уравнением (1.42) позволяет
предположить, что они идентичны. В самом деле, левая часть представляет
собой мощность сторонних источников электрического и магнитного типов,
которые были введены при постановке задачи (об этом свидетельствует
размерность слагаемых под знаком интеграла), причем знак минус означает,
что энергия сторонних источников расходуется в рассматриваемой области
пространства.
Первое слагаемое в правой части представляет собой тепловые потери
(мощность, расходуемую на нагрев вещества в рассматриваемой области). Об
этом говорит размерность интеграла, либо тот факт, что подинтегральное
выражение является дифференциальной формой известного из физики закона
Джоуля-Ленца. Следует обратить внимание на то, что при отсутствии
проводимости среды (γ = 0) тепловые потери отсутствуют.
Подинтегральное выражение во втором слагаемом правой части (1.43)
можно преобразовать к виду:
эa
W
t
E
tt
D
Е
∂
∂
=
∂
∂
=
∂
∂
)
2
(
2
ε
;
мa
W
t
H
tt
B
H
∂
∂
=
∂
∂
=
∂
∂
)
2
(
2
µ
,
где ε
а
2
2
Е
- плотность энергии электрического поля,
µ
а
2
2
Н
- плотность энергии магнитного поля.
Сумма этих слагаемых под знаком интеграла представляет собой
изменение во времени плотности энергии электромагнитного поля в
рассматриваемой области пространства. Т.о. рассмотренное выражение
эквивалентно третьему слагаемому (1.42).
Подинтегральное выражение в третьем слагаемом правой части (1.43)
является вектором, размерность которого (ВА/м
2
) характеризует его как
плотность потока мощности. Он носит название вектора Пойнтинга и
определяет величину и направление потока электромагнитной энергии.
Интеграл от вектора Пойнтинга по замкнутой поверхности характеризует
мощность, переносимую через эту поверхность. В зависимости от знака этого
интеграла электромагнитная энергия либо выходит, либо входит в объем,
ограниченный поверхностью. Таким образом, это слагаемое эквивалентно
второму слагаемому (1.42).
16
Доказанная теорема имеет громадное научно-техническое и
философское значение, поскольку подтверждает материальность
электромагнитного поля!
Вопросы для самопроверки
1. Каковы основные особенности электромагнитного поля, подтверждающие его
материальность?
2. В чем заключается физический смысл векторов, характеризующих электромагнитное
поле?
3. Какой вид имеют материальные уравнения для векторов электромагнитного поля?
4. Каковы классификации сред, применяющиеся в электродинамике?
5. Какие экспериментальные законы лежат в основе уравнений Максвелла?
6. В чем состоит физический смысл тока смещения?
7. Что связывают между собой уравнения Максвелла в интегральной и дифференциальной
формах?
8. В чем заключается разница между симметричной и несимметричной формами записи
уравнений Максвелла?
9. Какие энергетические составляющие могут входить в уравнение баланса энергии
электромагнитного поля?
10. Запишите выражение для вектора Пойнтинга в случае гармонических во времени полей.
2. Волновые уравнения и потенциалы электромагнитного поля
Решение задач электродинамики с помощью уравнений Максвелла
сводится обычно к решению так называемых волновых уравнений, которые
являются дифференциальными уравнениями в частных производных второго
порядка. На практике применяются три вида волновых уравнений – уравнения
для векторов поля
НЕ , , уравнения для электродинамических потенциалов UА,
и уравнение для вектора Герца
Г .
2.1 Волновые уравнения для векторов поля
В случае линейной, однородной, полупроводящей среды при наличии
сторонних источников только электрического типа волновые уравнения для
векторов поля могут быть получены на основе соответствующим образом
записанных уравнений Максвелла в виде:
ст
э
а
ст
э
аааа
grad
tt
Е
t
Е
Е
ρ
ε
δ
µγµεµ
1
2
2
2
+
∂
∂
=
∂
∂
−
∂
∂
−∇ , (2.1)
ааа
t
Н
Н
µεµ
−
∂
∂
−∇
2
2
2
ст
э
rot
t
Н
δγ
−=
∂
∂
. (2.2)
В этих выражениях все обозначения соответствуют обозначениям,
введенным ранее в разделе 1.
Уравнения (2.1), (2.2) являются векторными, волновыми, обобщенными,
неоднородными уравнениями.
В диэлектрической среде (γ =0) третье слагаемое в левой части равно
нулю, уравнения упрощаются и превращаются в уравнения Даламбера. Если в
рассматриваемой области пространства отсутствуют сторонние источники
(
ст
э
ст
э
ρδ
, = 0), то правые части обращаются в нуль и уравнения становятся
однородными.
17
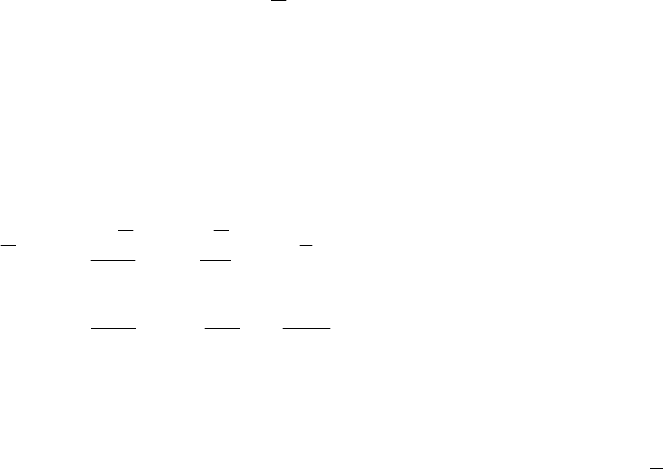
В самом общем случае решение электродинамической задачи с
помощью 2.1, 2.2 (отыскание векторов электромагнитного поля в каждой точке
пространства) требует решения шести скалярных волновых уравнений для
проекций этих векторов на координатные оси (решения шести краевых задач)
что, как правило, представляет значительные трудности.
Кроме того, наличие в правой части этих уравнений
дифференциальных операторов, под знаком которых находятся функции,
описывающие распределение источников, делает вообще невозможным
решение задачи в тех случаях, когда эти функции являются разрывными (на
границах раздела сред с различными электрическими параметрами).
Названные особенности с формальной точки зрения можно
рассматривать как недостатки рассмотренной формы уравнений, что привело к
появлению другой формы волновых уравнений – волновых уравнений для
электродинамических потенциалов.
2.2 Волновые уравнения для электродинамических потенциалов
Принято использовать векторный и скалярный электродинамические
потенциалы – соответственно
UА, . Если векторный потенциал физического
смысла не имеет, то скалярный – имеет смысл работы сил поля по
перемещению единицы количества электричества из рассматриваемой точки в
бесконечность.
При тех же условиях, что и в предыдущем разделе, на основе той же
системы уравнений Максвелла можно получить волновые уравнения для
рассматриваемых потенциалов:
.
2
2
2
ст
эаааа
t
А
t
А
А
δµγµεµ
−=
∂
∂
−
∂
∂
−∇
, (2.3)
γµεµ
ааа
t
U
U −
∂
∂
−∇
2
2
2
а
ст
э
t
U
ε
ρ
−=
∂
∂
. (2.4)
Уравнение (2.3) также как и уравнения (2.1) и (2.2) является векторным,
волновым, обобщенным неоднородным уравнением. Уравнение же (2.4)
является скалярным, волновым, обобщенным неоднородным уравнением. При
γ=0 они оба превращаются в уравнения Даламбера, а в случае
ст
э
δ
= ρ
э
ст
= 0 – в
однородные волновые уравнения.
Формально решение электродинамической задачи при помощи (2.3 –
2.4) состоит в решении четырех скалярных волновых уравнений (краевых
задач). Кроме того, в правой части этих уравнений находятся сами функции,
описывающие распределение источников, и решение задачи практически
всегда возможно. Т.о. недостатки, отмеченные в предыдущем разделе,
устранены.
Необходимо, однако, отметить, что в результате решения задачи
оказываются определенными лишь электродинамические потенциалы, а не
векторы поля. Для нахождения векторов поля необходимо провести
дополнительные математические вычисления (более простые, чем решение
краевой задачи) – решить уравнения, связывающие векторы поля с
электродинамическими потенциалами:
18
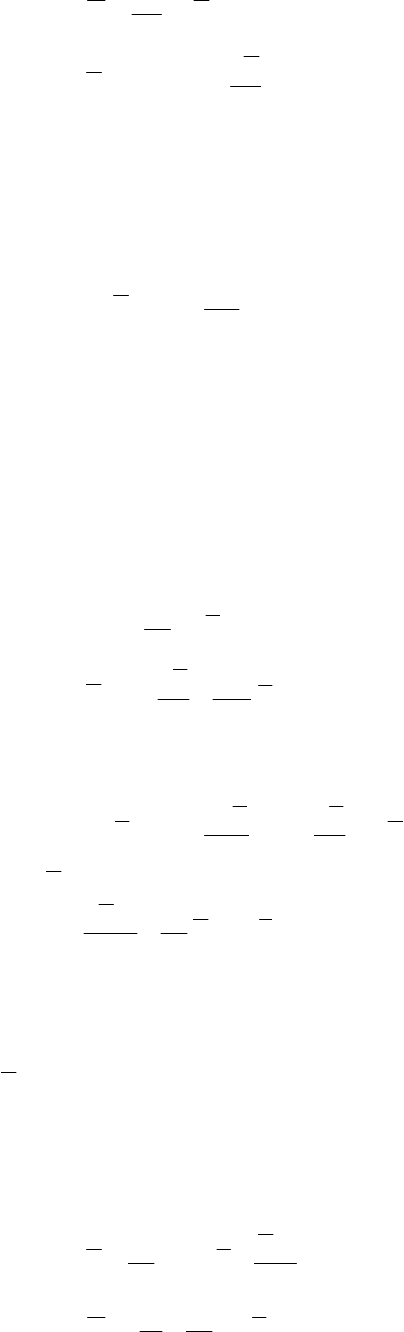
ArotН
а
µ
1
=
, (2.5)
t
A
qradUE
∂
∂
−−=
. (2.6)
Эти уравнения получаются из уравнений Максвелла при введении
электродинамических потенциалов. Ввиду того, что процедура введения
электродинамических потенциалов допускает некоторый произвол, то
волновые уравнения (2.3–2.4) обычно дополняют калибровочным
соотношением:
0=+
∂
∂
+ U
t
U
Adiv
ааа
γµεµ
, (2.7)
устанавливающим связь между введенными потенциалами.
2.3 Волновое уравнение для вектора Герца
Учитывая то обстоятельство, что векторный и скалярный потенциалы
связаны между собой калибровочным соотношением, имеется возможность
свести электродинамическую задачу к решению одного векторного волнового
уравнения (всего трех скалярных) для вектора Герца. Вектор Герца вводится
так, что его связь с векторным и скалярным потенциалами имеет следующий
вид:
ГdivU
а
ε
1
−= , (2.8)
.Г
t
Г
А
а
а
а
ε
γµ
µ
+
∂
∂
= (2.9)
Подстановка в волновое уравнение (2.8) либо (2.9) позволяет получить
векторное, волновое, обобщенное неоднородное уравнение для вектора Герца:
ст
ааа
Р
t
Г
t
Г
Г −=
∂
∂
−
∂
∂
−∇
γµεµ
2
2
2
, (2.10)
где
ст
Р
определяется из уравнения
ст
э
ст
а
ст
Р
t
Р
δ
ε
γ
=+
∂
∂
(2.11)
и имеет смысл удельного электрического момента сторонних токов.
Также как и в предыдущих разделах, равенство нулю удельной
электропроводности γ и удельного электрического момента сторонних токов
ст
Р
превращает (2.10) в уравнение Даламбера и однородное волновое
уравнение соответственно.
Решение (2.10) дает возможность найти вектор Герца; векторы
электромагнитного поля могут быть определены непосредственно через вектор
Герца с помощью соотношений:
а
ст
а
Р
ГrotrotЕ
εε
−=
1
, (2.12)
Гrot
t
Н
а
)(
ε
γ
+
∂
∂
=
. (2.13)
19
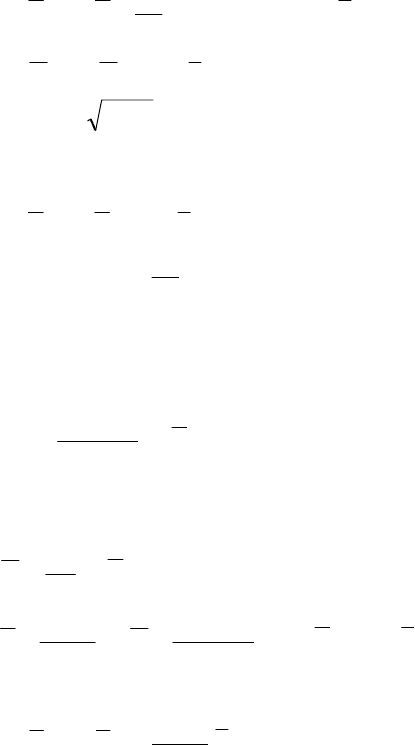
2.4 Волновые уравнения в комплексной форме
Также как и в разделе 1.9, в случае гармонических монохроматических
полей волновые уравнения можно упростить путем использования
символического метода. После введения комплексных величин и сокращения
множителя exp (jωt), опуская индекс «m» можно получить:
-для векторов поля –
ст
эа
ст
э
а
jgradЕкЕ
δωµρ
ε
&
&
&
&
&
+=+∇
1
22
, (2.14)
ст
э
rotНкН
δ
&
&
&
&
−=+∇
22
. (2.15)
Здесь:
κ
&
=
аа
µεω
&
- комплексная постоянная распространения (комплексное
волновое число);
-для электродинамических потенциалов –
ст
эа
АкА
δµ
&&
&
&
−=+∇
22
, (2.16)
ст
э
а
UкU
ρ
ε
&
&
&
&
1
22
−=+∇ . (2.17)
В рассматриваемом случае гармонических полей необходимость в
решении волнового уравнения для скалярного потенциала отпадает, поскольку
он может быть найден из калибровочного соотношения:
Adiv
j
U
аа
&
&
&
εωµ
1
−= . (2.18)
Более того, векторы поля в этом случае могут быть найдены из (2.5) и
первого уравнения Максвелла только через векторный потенциал:
,
1
ArotН
а
&
&
µ
= (2.19)
Arotrot
j
Hrot
j
Е
ааа
&
&
&
&
&
µεωεω
11
== (при 0=
ст
э
δ
&
); (2.20)
-для вектора Герца –
ст
э
а
а
j
ГкГ
δ
εω
ε
&
&
&&
−=+∇
22
. (2.21)
Решение этого уравнения практически не отличается от решения
уравнения для векторного потенциала.
Вопросы для самопроверки
1. Какие виды волновых уравнений используются для решения задач электродинамики?
2. В чем заключается смысл калибровочного соотношения?
3. В чем состоит отличие уравнений Даламбера и Гельмгольца от обобщенного волнового
уравнения?
4. Имеется ли разница между векторным потенциалом и вектором Герца в случае
гармонического электромагнитного поля?
3. Основные методы решения задач электродинамики
3.1 Формулировка задач электродинамики
Большинство задач антенной техники, техники сверхвысоких частот и
распространения радиоволн можно свести к нескольким абстрактным
20
