Lefebvre A.H., Ballal D.R. Gas Turbine Combustion: Alternative Fuels and Emissions
Подождите немного. Документ загружается.


270 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition
6.21.2 Pressure-Swirl Atomizers
The discharge coefcient of a swirl atomizer is inevitably low, owing to the
presence of the air core, which effectively blocks off the central portion of the
orice. Radcliffe [82] studied the performance of a family of injectors based
on common design rules, using uids that covered wide ranges of density
and viscosity. He noted that the effect of an increase in viscosity is to thicken
the uid lm in the nal orice, thereby raising the discharge coefcient.
This effect can be signicant at low ow rates with nozzles of small ow
number. However, for Reynolds numbers larger than 3000, that is, over most
of the normal working range, the discharge coefcient is practically indepen-
dent of Reynolds number. Thus, for fuels of low viscosity, the convention is
to disregard conditions at low Reynolds number and assume that any given
atomizer has a constant discharge coefcient.
According to Giffen and Muraszew [83], the discharge coefcient of a pres-
sure-swirl atomizer is related to atomizer dimensions and the area of the air
core by the equations
CXX
D
/=−+1171 1
305
.[()()],
.
(6.43)
where
X
A
A
d
===
−
Aircorearea
Dischargeorifice area
a
o
o
2tt
d
(
)
2
2
o
,
(6.44)
where t is the fuel lm thickness in the discharge orice.
Several other equations for discharge coefcients have been derived
[58]. The following relationship, which is based on the analysis of a large
amount of experimental data by Rizk and Lefebvre [84], is illustrated in
Figure 6.35.
C
A
Dd
D
d
D
p
so
s
o
=
036
05
025
..
.
.
(6.45)
6.21.3 Film Thickness
In pressure-swirl atomizers, the fuel emerges from the nozzle as a thin
conical sheet that rapidly attenuates as it spreads radially outward, nally
disintegrating into ligaments and then drops. In prelming airblast atom-
izers, the fuel is also spread out into a thin continuous sheet before being
exposed to high-velocity air. It is of interest, therefore, to examine the factors
that govern the thickness of this fuel lm.
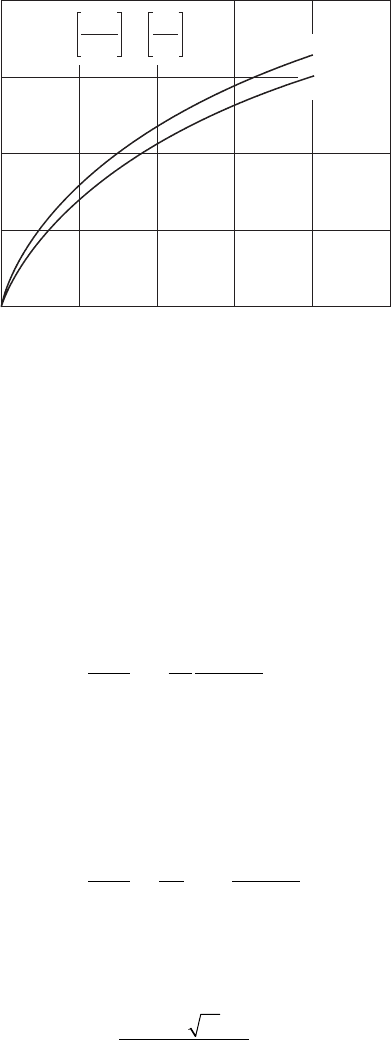
Fuel Injection 271
For both pressure-swirl and airblast types of atomizers, it has long been rec-
ognized that the thickness of the annular fuel lm produced at the nozzle exit
has a strong inuence on the mean drop size of the spray. In pressure-swirl
atomizers, the thickness of this lm is directly related to the area of the air
core, as indicated in Equation 6.44. Giffen and Muraszew’s analysis of the ow
conditions within a simplex nozzle, assuming a nonviscous uid, led to the fol-
lowing relationship between atomizer dimensions and the size of the air core:
A
Dd
X
X
p
so
=
−
(
)
2
2
3
2
32
1
π
.
(6.46)
After calculating X from Equation 6.46, the corresponding value of lm
thickness t is then obtained from Equation 6.44.
A similar relationship between atomizer dimensions and the size of the air
core was derived by Suyari and Lefebvre [85].
009
1
1
2
05
3
..
.
A
Dd
D
d
X
X
p
so
s
o
=
−
(
)
+
(6.47)
Simmons and Harding [86] derived the following simple equation for fuel
lm thickness in terms of nozzle ow number and spray cone angle.
t
d
=
0 00805.
cos
.
ρ
θ
L
o
FN
(6.48)
0.8
0.6
Discharge coefficient, C
D
0.4
0.2
0
0 0.4 0.8 1.2
A
p
/D
s
d
o
1.6 2.0
D
s
/d
o
=3.5
D
s
/d
o
=5
C
D
=0.35
0.5
A
p
D
s
d
o
0.25
D
s
d
o
Figure 6.35
Relationship between discharge coefcient and atomizer dimensions.
272 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition
Suyari and Lefebvre tested the validity of these and other equations for lm
thickness by comparing predicted values with their measured values using
water as the working uid. They found that Equations 6.47 and 6.48 provide
a good t to the experimental data. However, these equations do not take
into account the effects of fuel properties and nozzle pressure drop on lm
thickness.
Rizk and Lefebvre [84] used a theoretical approach to investigate the inter-
nal ow characteristics of pressure-swirl atomizers. A general expression for
lm thickness was derived in terms of atomizer dimensions, liquid proper-
ties, and liquid injection pressure as
t
m
dP
X
X
2
2
1560 1
1
=
+
−
(
)
LL
Lo L
µ
ρ∆
.
(6.49)
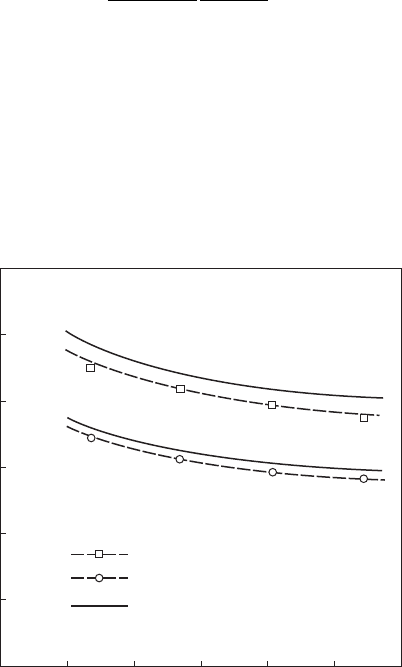
Rizk and Lefebvre [84] used this equation to calculate lm thicknesses for
different nozzle dimensions and operating conditions. Some of their results
are shown in Figure 6.36 as plots of lm thickness against injection pres-
sure differential. Also shown in this gure are the measured values of Kutty
et al. [87,88]. Theory and experiment both indicate that a higher pressure
drop produces a thinner lm. Thus, the improvement in atomization quality
Experiment [87, 88]
0
0
0.08
0.16
0.24
t, mm
0.40
0.32
0.48
12
∆P, MPa
3
d
o
= 2.4 mm
d
o
= 1.2 mm
Equation (6.49)
Figure 6.36
Variation of lm thickness with injection pressure for different orice diameters. (From Rizk,
Ν.Κ., and Lefebvre, A.H., Journal of Propulsion and Power, 1(3), 93–199, 1985. With permission.)
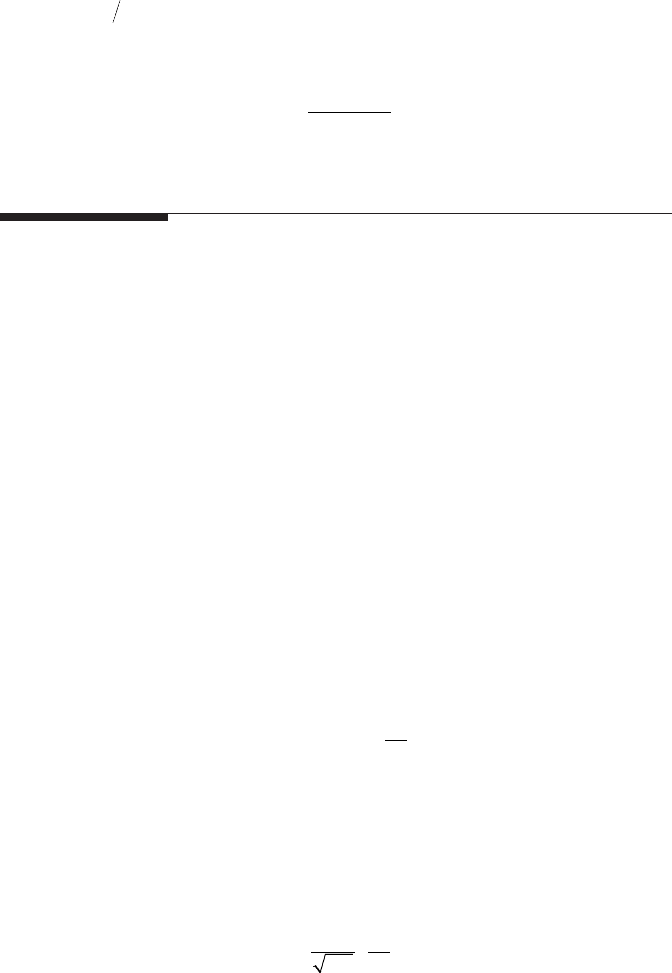
Fuel Injection 273
that always accompanies an increase in nozzle pressure drop is due in some
measure to the concomitant decrease in lm thickness.
A drawback to Equation 6.49 is that because X is dependent on t (see
Equation 6.44), some trial-and-error procedures are involved in its solution.
However, if
td
o
1
, it can be written more succinctly, while still retaining
its essential features, as
t
d
P
=
(
)
27
05
025
..
.
.
oL
LL
FNµ
ρ∆
(6.50)
6.22 Spray Cone Angle
An important aspect of atomizer design, in addition to achieving the desired
drop-size distribution, is to ensure that the droplets formed in atomization
are discharged from the nozzle in the form of a symmetrical uniform spray.
In general, an increase in spray cone angle increases the exposure of the
droplets to the surrounding air or gas, leading to improved atomization and
to higher rates of heat and mass transfer.
6.22.1 Plain-Orifice Atomizers
With plain-orice atomizers, the cone angle is narrow and the drops are
fairly evenly dispersed throughout the entire spray volume. The angle of the
spray is normally dened as the angle formed by two straight lines drawn
from the discharge orice to the outer periphery of the spray at a distance 60
d
o
downstream of the nozzle. Several formulae have been derived to express
the spray angle in terms of nozzle dimensions and the relevant air and liquid
properties. The simplest expression for the spray angle is given by the jet
mixing theory of Abramovich [89] as
tan. .θ= +
0131
ρ
ρ
A
L
(6.51)
According to Reitz and Bracco [90], the spray angle can be determined by
combining the radial velocity of the fastest growing of the unstable surface
waves with the axial injection velocity. This hypothesis results in the follow-
ing expression for the spray angle:
tan.
.
θ
πρ
ρ
=
2
3
05
A
A
L
(6.52)
274 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition
Yokota and Matsuoka [91] and Hiroyasu and Arai [92] have derived correla-
tions for their experimental data on spray angles obtained at high ambient
air pressures. These and other equations for the spray cone angles of plain-
orice atomizers are presented and discussed in References [58] and [92].
Ohrn et al. [93] used 40 different plain-orice atomizers to examine the effects
of nozzle geometry and ow conditions on spray cone angle. Some of their
results, showing the effects of nozzle pressure differential and orice length/
diameter ratio on the cone angle for round-edged inlets, are presented in
Figure 6.37. The main conclusion from this study is that the cone angle increases
with injection pressure for sharp-edged and slightly radiused inlet nozzles, but
is largely independent of injection pressure for highly radiused inlets.
6.22.2 Pressure-Swirl Atomizers
In most combustion applications, the spray is in the form of a hollow cone of
wide angle, with most of the drops concentrated at the periphery. A major
difculty in the denition and measurement of the cone angle is that the
spray cone has curved boundaries, owing to the effects of air interaction
with the spray. To overcome this problem, the cone angle is often given as
the angle formed by two straight lines drawn from the discharge orice to
cut the spray contours at some specied distance from the atomizer face.
6.22.2.1 Theoretical Aspects
During the last half-century, several expressions for the spray cone angle have
been derived, usually with the assumption of inviscid ow. Taylor’s [94] invis-
cid theory showed that the spray cone angle is determined solely by the swirl
chamber geometry and is a unique function of the ratio of the inlet ports area to
the product of swirl chamber diameter and orice diameter, A
p
/D
s
d
o
, as shown
l/d = 4
Rounded inlet
20
Cone angle, degrees
15
10
5
0
020406080
Injection pressure, MPa
100 120
r/d = 0.05
r/d = 0.19
r/d = 0.24
r/d = 0.50
Figure 6.37
Spray cone angles for rounded inlets; l
o
/d
o
= 4.
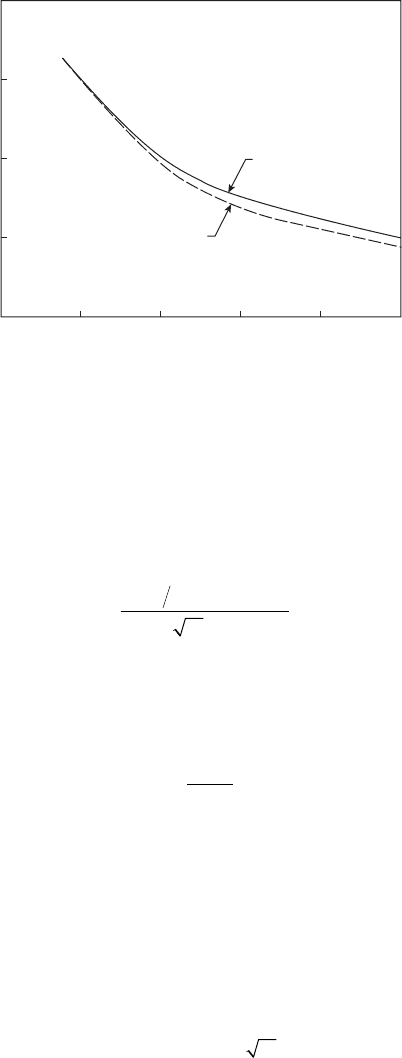
Fuel Injection 275
in Figure 6.38. The solid curve in this gure corresponds to experimental data
obtained by several workers (see Reference [58]). Giffen and Muraszew’s [83]
analysis also assumed a nonviscous uid, which allowed the spray cone angle
to be expressed as a function of nozzle dimensions only. It led to the following
expression for the mean value of the spray cone half angle θ.
sin,
.
.
θ
π
=
(
)
−
(
)
+
(
)
+
(
)
21
11
15
05
X
KXX
(6.53)
where Κ = A
p
/D
s
d
o
and X = A
a
/A
0
.
Rizk and Lefebvre’s [84] inviscid ow analysis also led to a unique rela-
tionship between the cone angle and X of the form
cos
2
θ=
−
+
1
1
X
X
,
(6.54)
where X depends solely on the atomizer dimensions, as indicated in
Equation 6.44.
In the above equations, θ is the cone half-angle, as measured close to the
nozzle. As the spray in this region has a small but denite thickness, the cone
angle formed by the outer boundary of the spray is dened as 2θ, whereas
2θ
m
represents the mean cone angle in this near-nozzle region. By assuming
a constant axial velocity across the liquid lm, the maximum cone angle is
related to the mean cone angle by the expression [84]
tan
m
θθ=+
(
)
05 1.tan .X
(6.55)
Inviscid theory
Experiment
120
Spray cone angle, degrees
100
80
60
40
0 0.2 0.4 0.6
A
p
/D
s
d
o
0.8 1.0
Figure 6.38
Relationship between spray cone angle and atomizer geometry.

276 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition
The equations quoted above for the spray cone angles of pressure-swirl atom-
izers are valid only for liquids of low viscosity, such as water or kerosine.
Rizk and Lefebvre [95] used a theoretical approach to derive the following
dimensionally correct equation for viscous liquids:
26
015
2
2
011
θ
µ
=
Dd
A
d
so
p
LoL
L
PP
.
.
.
∆
(6.56)
According to this equation, the spray cone angle is widened by increases
in discharge orice diameter, liquid density, and injection pressure, and is
diminished by an increase in liquid viscosity.
6.23 Radial Fuel Distribution
The symmetry of the spray patterns produced in atomization is of consider-
able importance because the fuel must be distributed uniformly throughout
the combustion zone to achieve high combustion efciency, low pollutant
emissions, and a uniform distribution of temperature in the combustor efux
gases. Although the visible spray cone angle gives some indication of spray
symmetry and the total dispersion of a spray, it provides little or no informa-
tion on how the fuel mass ux is distributed radially and circumferentially
within the spray volume.
The term adopted by the gas turbine industry for the purpose of dening
spray distribution is “patternation” and the instruments used to measure
fuel ux distributions in sprays are commonly referred to as “patternators.”
A typical radial patternator consists of a number of small collection tubes
oriented equidistant radially from the origin of the spray, as shown schemat-
ically in Figure 6.39. The sampling tubes are allowed to ll with fuel until
one of the tubes is nearly full. At that point, the fuel supply is turned off and
the volume of fuel in each tube is measured by visually locating the menis-
cus between lines scribed into the clear plastic of the patternator. Radial
distribution curves are made by plotting fuel volume as the ordinate and
the corresponding angular location of the sampling tubes as the abscissa,
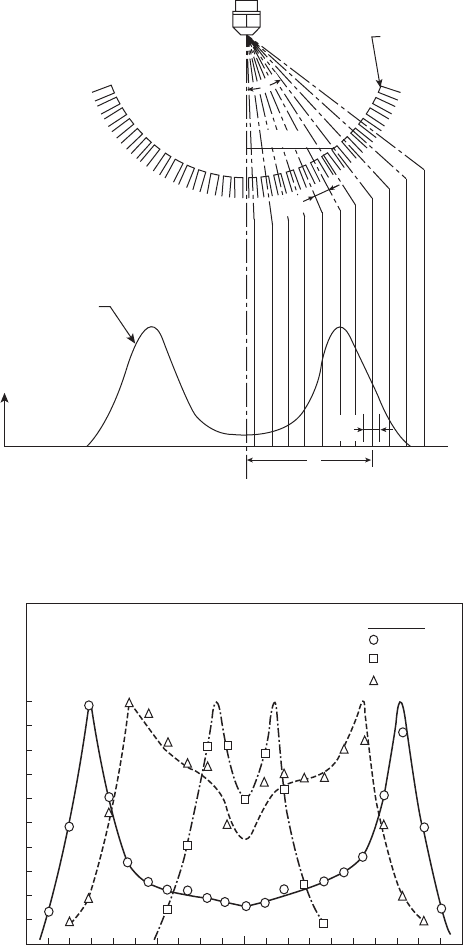
as illustrated in Figure 6.39. A typical plot is shown in Figure 6.40; it illus-
trates how the spray cone angle of a pressure-swirl atomizer contracts with
an increase in ambient air pressure.
To more succinctly describe the effect of changes in operating param-
eters on fuel distribution, a radial distribution curve may be reduced to a
single numerical value, called the effective or equivalent spray angle [56,96].
The effective spray angle, 2θ, is the sum of two angles, 2θ = θ
L
+ θ
R
, where
θ
L
(or θ
r
) is the value of θ that corresponds to the position of the center
Fuel Injection 277
∆θ
∆θ
∆θ = 4.5°
r = 10 cm
CC of fuel
Spray
distribution
curve
Nozzle
Sampling
tubes
θ
Nozzle axis
r sin θ
θ
Figure 6.39
Measurement of radial fuel distribution.
0.101
P
A
, MPa
0.380
Simplex atomizer
Liquid = kerosine
∆P
L
= 0.76 MPa
1.0
Normalized fuel volume
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
50 40 30 20 10 010
Spray half angle, deg.
20 30 40 50
0.74
Figure 6.40
Inuence of ambient air pressure on radial fuel distribution. (From Ortman, J., and Lefebvre,
A.H., Journal of Propulsion and Power, 1(1), 11–15, 1985. With permission.)
278 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition
of mass of a material system for the left (or right) lobe of the distribution
curve. For hollow-cone, pressure-swirl atomizers, the effective spray angle
tends to be from 5° to 15° smaller than the normal spray angle, as observed
visually.
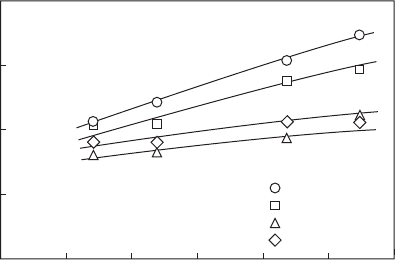
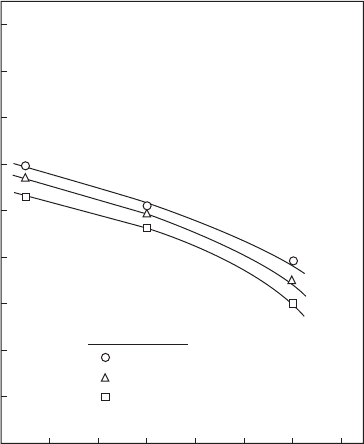
Figure 6.41 shows the results of measurements carried out by Chen et al.
[97] on the effects of injection pressure and liquid viscosity on equivalent
spray cone angle. It is noteworthy that the trends exhibited by the curves
drawn in this gure are consistent with the predictions of Equation 6.56
in demonstrating that the spray angle is increased by an increase in injec-
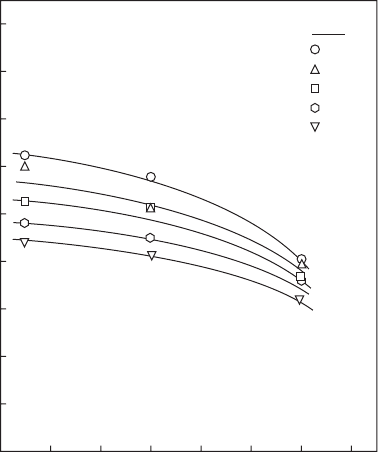
tion pressure and/or a reduction in fuel viscosity. Chen et al. also examined
the effect on the spray angle of varying the l
o
/d
o
ratio of the nal discharge
orice. As shown in Figure 6.42, the spray angle is reduced by an increase
in l
o
/d
o
. Changing the number of swirl-chamber feed slots between one and
three was found to have little effect on the spray angle.
The sprays produced by prelming airblast atomizers are much less sus-
ceptible to variations in fuel and ambient air pressure than sprays from
pressure-swirl atomizers. The fuel sheet exposed to the atomizing air has
relatively little momentum and the droplets formed in atomization are
90
80
70
60
Effective spray angle, degrees
50
40
30
20
10
0
02468
Liquid viscosity, kg/ms
Simplex atomizer
FN = 8 × 10
–8
m
2
l
o
/d
o
= 1.0
∆P
L
, MPa (psi)
1.72 (250)
1.38 (200)
1.03 (150)
10 12 14 × 10
–3
Figure 6.41
Inuence of liquid viscosity and injection pressure on effective spray angle. (From Chen, S.K.,
Lefebvre, A.H., and Rollbuhler, J., Journal of Engineering for Gas Turbines and Power, 114, 97–103,
1992. With permission.)
Fuel Injection 279
largely dependent on the kinetic energy of the atomizing air to transport
them away from the nozzle. This means that droplet trajectories are gov-
erned mainly by the air movements created by air swirlers and other aero-
dynamic devices that form an integral part of the nozzle conguration. Thus,
the spray structure of airblast atomizers is not overly sensitive to the physical
properties of the fuel and the surrounding gaseous medium.
Recent work by Zheng et al. [73,74] on a counter-rotating, prelming air-
blast atomizer owing kerosine fuel has shown that the main factor govern-
ing the spray cone angle is the fuel/air momentum ratio. Increases in this
parameter result in wider cone angles, which indicate a displacement of the
fuel ux prole toward the outer boundaries of the spray. For the engine fuel
nozzle used in this investigation, it was found that increasing the air pres-
sure from 1 to 12 bar at a constant AFR caused the initial fuel spray angle
to widen from 85° to 105°. No general conclusions should be drawn from
these results because they may relate only to the type of nozzle tested. What
they do demonstrate is that the radial distribution of fuel droplets through-
out the spray volume is not solely dictated by the atomizing airow pattern,
90
80
70
60
Effective spray angle, degree
50
40
30
20
10
0
02468
Liquid viscosity, kg/ms
Simplex atomizer
FN = 8 × 10
–8
m
2
∆P
L
= 1.72 MPa (250 psi)
l
o
/d
o
10 12 14 × 10
–3
0.5
1.0
2.0
3.0
4.0
Figure 6.42
Inuence of discharge orice length/diameter ratio on effective spray angle. (From Chen, S.K.,
Lefebvre, A.H., and Rollbuhler, J., Journal of Engineering for Gas Turbines and Power, 114, 97–103,
1992. With permission.)
