Lefebvre A.H., Ballal D.R. Gas Turbine Combustion: Alternative Fuels and Emissions

Подождите немного. Документ загружается.

260 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

Based on these considerations, Lefebvre [62] adopted an alternative approach

to the derivation of an equation for mean drop size. For the purpose of analy-

sis, the atomization process was treated in two separate stages. The rst stage

represents the generation of surface instabilities due to the combined effects

of internal hydrodynamic and external aerodynamic forces. The second stage

is the conversion of surface protuberances into ligaments and drops. This sub-

division allows the formulation of an equation for mean drop size as

SMD

LA LL

(

)

(

)

+452039

025025

.cos .

σµ ρθσρ∆Pt ρρθ

∆Pt

(

)

(

)

025075..

cos,

(6.25)

where t is the lm thickness within the nal discharge orice (see Figure 6.28)

and θ is the half-angle of the spray.

This equation takes into account all the factors that are known to affect the

drop sizes produced in pressure-swirl atomization, including the cone angle

of the spray. An increase in the cone angle improves atomization by reduc-

ing the thickness of the liquid sheet after it is discharged from the nozzle, as

illustrated in Figure 6.28.

The values of the constants 4.52 and 0.39 in Equation 6.25 were obtained

from a detailed experimental study carried out by Wang and Lefebvre [63],

in which measurements of SMD were made using six simplex nozzles of dif-

ferent sizes and spray cone angles. Several different liquids were employed

to provide a range of viscosity from 10

−6

to 18 × 10

−6

kg/ms (1–18 cS) and a

range of surface tension from 0.027 to 0.073 kg/s

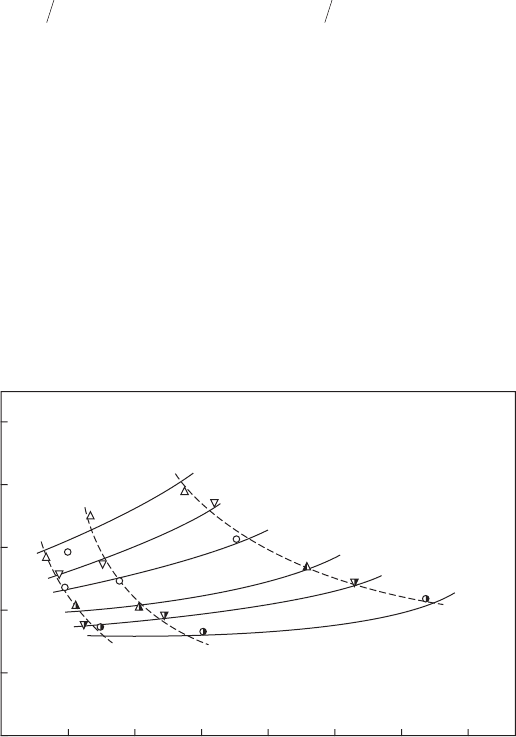
(27–73 dyn/cm). Figure 6.29

∆P

, MPa

Simplex nozzles

Cone angle - 60°

Fuel - DF-2

- 0.1 MPa

FN × 10

–8

0.53

0.35

0.69

1.04

1.38

2.07

100

SMD, µm

0246

Fuel flow rate, kg/s × 10

–3

8101214

Figure 6.29

Graphs illustrating relationship between SMD and nozzle operating variables for a spray cone

angle of 60°. (From Wang, X.F. and Lefebvre, A.H., Journal of Propulsion and Power, 3(1), 11–18, 1987.

With permission.)

Fuel Injection 261

is typical of the results obtained from this investigation. It shows the effect of

variations in fuel-injection pressure, fuel ow rate, and nozzle ow number,

on SMD for light diesel oil.

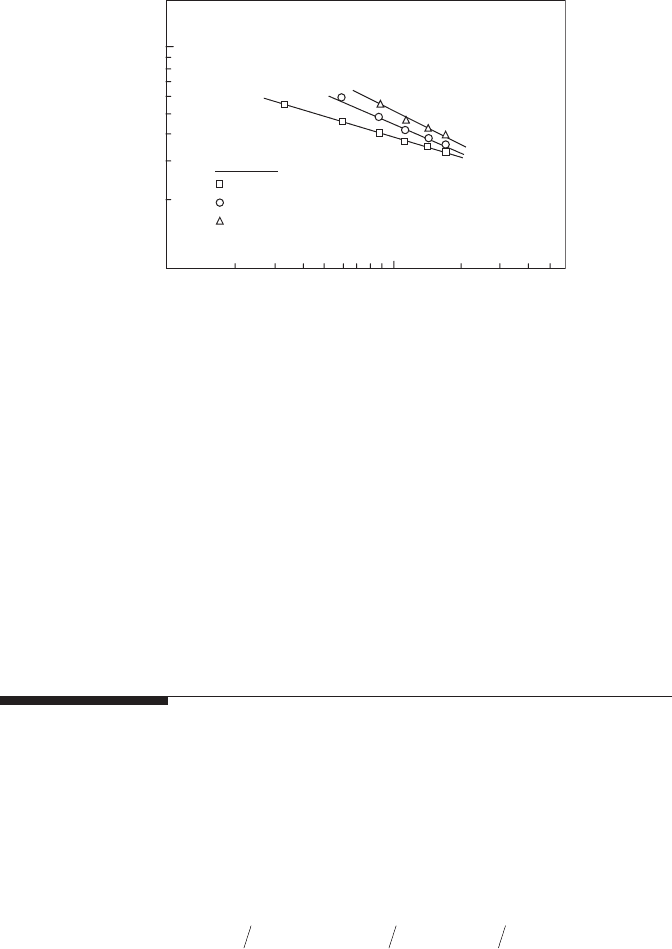
Inspection of Equation 6.25 reveals some interesting features that are dis-

cussed in detail in Reference [58]. For example, it suggests that liquids of high

viscosity should exhibit a higher dependence of SMD on injection pressure

differential ΔP

than liquids of low viscosity, and this is borne out by the

results presented in Figure 6.30.

6.17 SMD Equations for Twin-Fluid Atomizers

The rst major study of twin-uid atomization was conducted a half-century

ago by Nukiyama and Tanasawa [29] on a plain-jet airblast atomizer. Drop

sizes were measured by collecting samples of the spray on oil-coated glass

slides. The experimental data were correlated by the following empirical

equation for SMD:

SMD

LR LL LA

(

)

(

)

(

)

0585 53

0 225 1

σρ µσρUQQ

(6.26)

This equation is not dimensionally correct, but could be made so by intro-

ducing some atomizer characteristic dimension, L

, raised to the power 0.5.

An obvious choice for this dimension is either the diameter of the liquid

discharge orice or the diameter of the air nozzle at exit. However, from tests

Slope

100

SMD, µm

–0.31 –0.44 –0.48

Pressure-swirl atomizer

, kg/ms

0.001

0.006

0.012

0.1 0.2 0.4 0.7 1.0

∆P

, MPa

4.02.0

Figure 6.30

Inuence of liquid viscosity on relationship between SMD and injection pressure. (From Wang,

X.F., and Lefebvre, A.H., Journal of Propulsion and Power, 3(1), 11–18, 1987. With permission.)

262 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

carried out with different sizes and shapes of nozzles and orices, Nukiyama

and Tanasawa concluded that these dimensions have virtually no effect on

mean drop size. Thus, the absence of any atomizer dimension is a notable

feature of Equation 6.26.

For the classical mechanism of jet and sheet breakup, it is generally found

that experimental data on mean drop size are correlated very satisfactorily

by equations in which SMD/L

is expressed in terms of ALR, Weber num-

ber, and Ohnesorge number [64]. The so-called “basic” equation is usually

expressed as

SMDSMD SMD=+

(6.27)

Analysis of the factors governing SMD

and SMD

leads to

SMDALR We Oh

LAB1

10505

(

)

−−..

(6.28)

SMDALR

cAAp LLP

LAUD BD=+

(

)









(

)

−

σρ µσρ

((

)

{}

05.

(6.29)

where A and B are constants whose values depend on atomizer design. For

plain-jet atomizers, L

is the initial liquid jet diameter, d

. For prelming

atomizers, L

is the initial thickness of the liquid sheet.

With practical atomizers, various design features and internal ow effects

tend to modify the basic equation for SMD to forms as shown in Equations

6.30 and 6.31. Thus, for example, Rizk and Lefebvre [64] used their measured

values of SMD to derive the following dimensionally correct equation for the

mean drop sizes produced by a plain-jet airblast atomizer.

SMDALR

[]

(

)









−

0481

04 1

dUdσρ

551

05 1

ddµσρ

ALR

[]

(

)









−.

(6.30)

This equation was shown to provide an excellent data correlation, espe-

cially for low-viscosity fuels. Lorenzetto and Lefebvre [65] and Jasuja [66]

also derived very similar expressions for plain-jet airblast atomizers, thereby

conrming the general validity of this form of predictive equation.

For prelming airblast atomizers, El-Shanawany and Lefebvre [67] found

that mean drop sizes could be correlated satisfactorily by the following

dimensionally correct equation:

Fuel Injection 263

SMD

ALR

ARpAL

UD=+

(

)









(

)

(

)

−

1033

σρ ρρ

0068+

(

)









µσρ

LLp

(6.31)

where D

is the hydraulic diameter of the air exit duct and D

is the prelmer

diameter. Equations 6.30 and 6.31 show that SMD always increases with an

increase in liquid viscosity, although the effect may be small for liquids of

low viscosity due to the relatively small magnitude of the SMD2 term in

these equations.

Usually it is found that an increase in surface tension serves to increase the

mean drop size (by reducing the Weber number), but this is because most

liquid hydrocarbon fuels tend to have relatively low viscosities and the SMD

is dominated by the rst term on the right hand side of Equations 6.30 and

6.31. However, these equations also predict that an increase in liquid viscosity

causes the inuence of surface tension on SMD to decline until a critical value

of viscosity is eventually attained, above which any further increase in sur-

face tension actually serves to reduce the mean drop size. The physical expla-

nation for these seemingly contradictory effects is that surface tension forces

assist viscosity in damping oscillations for the short-wavelength disturbances

associated with liquids of low viscosity, but enhance oscillation growth for

the long-wavelength disturbances associated with liquids of high viscosity.

Equations 6.30 and 6.31 also show that a continuous increase in relative

velocity, U

, causes SMD

to decline, so that SMD becomes more sensitive

to changes in liquid viscosity (via SMD

). This result conicts with the nd-

ings of Buckner and Sojka [68], Sattelmayer and Wittig [69] and Beck et al.

[10], all of whom observed only a small effect of liquid viscosity on SMD at

high atomizing air velocities. The reason for this apparent contradiction is

that Equations 6.30 and 6.31 are based implicitly on the notion that drop-

lets are produced by the classical mechanisms of jet and sheet breakup and,

in fact, the experimental data used to derive these equations were obtained

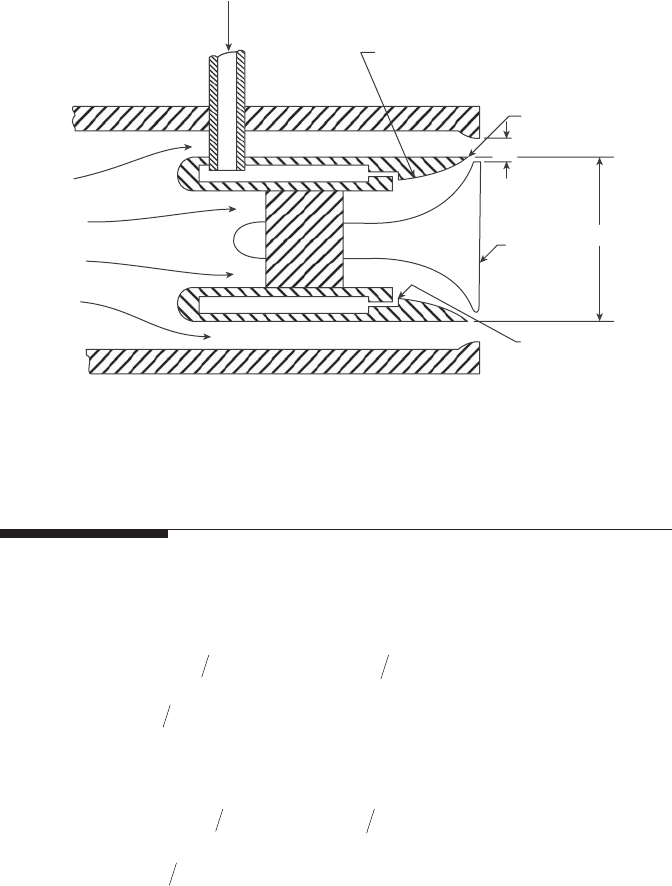
using atomizers in which the air and liquid were essentially co-owing (see

Figures 6.31 and 6.32). As discussed above, these conditions are highly con-

ducive to the classical mechanisms of jet and sheet breakup.

Air

Liquid

Air

Figure 6.31

Schematic of co-owing, plain-jet airblast atomizer.

264 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

6.18 SMD Equations for Prompt Atomization

For sheet disintegration we have [9]

SMDWeALRt =+ +

(

)

{}

−

31 0001751

(6.32)

where

=ρ σ.Ut

For jet breakup by the prompt mechanism, the corresponding expression

SMDWeALRdC

15 11=+ +

(

)

{}

−

(6.33)

where

=ρ σUd

, and the value of C depends on the various design

features that govern the utilization efciency of the atomizing air.

Figure 6.33 shows a comparison between measured values of SMD and pre-

dicted values from Equation 6.33. In deriving this plot, Goris [70] employed

a value for C of 0.000144, but in the air-spray paint nozzle he used, a large

proportion of the total airow served only as shaping air and made no con-

tribution to the atomization process. If this is taken into account, a more

accurate value for C would be around 0.00084. However, as the efciency of

Note: D

= 2d

Weir

Pintle

Atomizing lip

Prefilming surface

Liquid

Air

Figure 6.32

Schematic of co-owing, prelming airblast atomizer.

Fuel Injection 265

air utilization can vary widely from one atomizer design to another, for any

given atomizer design the value of C should be determined experimentally.

According to Equations 6.29 through 6.31, for liquids of low viscosity, the

mean drop size in the spray should diminish with the increase in ambient air

pressure, according to the relationship SMD

αP

−05.

. Pressure exponents close

to −0.5 have, in fact, been obtained by a number of workers [64,66,67,71,72],

using atomizer designs of the type shown in Figures 6.31 and 6.32, in which

the air and liquid are co-owing. However, tests carried out by Zheng et al.

[73,74] on a more practical form of airblast atomizer (see Figure 6.18) in which

the fuel lm is injected into the highly turbulent region created at the inter-

face between two counter-rotating swirling airows, showed that SMD was

virtually independent of P

over the entire test range from 1 to 12 bar. This

result conforms to the predictions of Equation (6.32) for the prompt mecha-

nism of sheet breakup.

6.18.1 Comments on SMD equations

The atomization literature is replete with equations for correlating and pre-

dicting the mean drop sizes produced by various types of pressure and

twin-uid atomizers. All these equations should be used with caution, with

proper judgment being exercised in regard to the accuracy of the experimen-

tal data and the ranges of fuel and air properties and atomizer operating

conditions covered in the experiments.

It should be noted that no single equation can satisfactorily predict the drop

sizes produced by any given type of atomizer over its entire range of operation.

If a twin-uid atomizer is designed to produce fuel and airstreams that are

Equation (6.33)

Liquid – water

= 1.38 g/s

Experiment

100

SMD, µm

Air/liquid mass ratio

0123456

Figure 6.33

Comparison of measured values of SMD and predicted values from Equation 6.33. (From

Goris, N.H., MSME Thesis, Purdue University, 1990.)

266 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

essentially co-owing, then Equations 6.30 and 6.31 would be most appropri-

ate. If, on the other hand, the design is such that it favors prompt atomization,

then Equations 6.32 or 6.33 would be more suitable. For most twin-uid atom-

izers, it is inevitable that a range of operating conditions will exist over which

the mode of atomization will be in the transition regime between classical and

prompt and none of the SMD equations quoted above would be satisfactory.

The same reasoning applies with equal force to pressure atomizers. For

pressure-swirl atomizers operating at pressure differentials below around 1

MPa (145 psi), the classical mode of breakup predominates, and drop sizes are

markedly affected by variations in fuel viscosity. With a continuous increase

in pressure differential, the mode of atomization gradually changes from

classical to prompt until, at a ΔP

of around 3 MPa, the prompt mechanism is

dominant and mean drop sizes become more dependent on surface tension

and much less dependent on fuel viscosity. Normally, there is no clear demar-

cation between classical and prompt atomization; the change from one mode

to the other taking place slowly as the pressure differential is either gradu-

ally increased from a low value or gradually reduced from a high value. The

situation is analogous to airblast atomizers in that prompt atomization is pro-

moted by increases in Δ/V and reductions in liquid viscosity, corresponding

to increases in the Weber number and the Reynolds number, respectively.

6.19 Internal Flow Characteristics

In twin-uid atomizers of the airblast and air-assist types, atomization

and spray dispersion tend to be dominated by air momentum forces, with

hydrodynamic processes playing only a secondary role. With pressure-swirl

nozzles, however, the internal ow characteristics are of primary impor-

tance, because they govern the thickness and uniformity of the annular fuel

lm formed in the nal discharge orice, as well as the relative magnitude of

the axial and tangential components of velocity of this lm. It is, therefore, of

great practical interest to examine the inter-relationships that exist between

internal ow characteristics, nozzle design variables, and important spray

features such as cone angle and mean drop size.

6.20 Flow Number

The effective ow area of a pressure atomizer is usually described in terms

of a ow number, which is expressed as the ratio of the nozzle throughput to

the square root of the fuel-injection pressure differential. Two denitions of

Fuel Injection 267

ow number are in general use: a British version, based on the volume ow

rate, and an American version, based on the mass ow rate. They are

Flow rate,UKgals./hr

Injectionpressure di

ffferential, psi

0.5

(

)

(6.34)

and

Flow rate,1b/hr

Injectionpressure differ

USA

eential,psi

0.5

(

)

(6.35)

Note that 1 UK gallon = 1.2 US gallons.

Equations 6.34 and 6.35 have the advantage of being expressed in units that

are in general use. Unfortunately, they are basically unsound. For example,

they do not allow a xed and constant value of ow number to be assigned

to any given nozzle. Thus, although it is customary to stamp or engrave a

value of ow number on the body of a simplex atomizer, this value is cor-

rect only when the nozzle is owing a standard calibrating uid of density

765 kg/m

. In the past, this has posed no problems with aircraft gas turbines

because 765 kg/m

roughly corresponds to the density of aviation kerosine.

However, for fuels of other densities, these two denitions of ow number

could lead to appreciable errors when used to calculate mass ow rates or

injection pressures.

The basic deciency in Equations 6.34 and 6.35 is the omission of fuel den-

sity. Inclusion of this property would not only allow these equations to be

rewritten in a dimensionally correct form, but would also enable the ow

number to be dened in a much more positive and useful manner than

at present, namely, as the effective ow area of the nozzle. Thus, the ow

number of any given nozzle would have a xed and constant value for all

liquids.

By including density, the ow number in square meters is obtained as

Flow rate, kg/s

Pressure differential, Pa

(

)

00.5

0.5

Liquid density, kg m

(

)

(6.36)

The standard UK and US ow numbers may be calculated from Equation

6.36 using the formulae:

FN FN,

UK L

=×××

−

06610

805

(6.37)

FN FN.

US L

=×××

−

06610

605

(6.38)

268 Gas Turbine Combustion: Alternative Fuels and Emissions, Third Edition

By combining Equations 6.36, 6.40, and 6.45, the ow number of a pressure-

swirl atomizer is obtained in terms of atomizer dimensions as

0ps

−

0389

12505025

...

dAD

(6.39)

6.21 Discharge Coefcient

The discharge coefcient of a pressure atomizer is governed partly by the

pressure losses incurred in the nozzle ow passages and also by the extent

to which the fuel owing through the nal discharge orice makes full use

of the available ow area. Discharge coefcient is related to nozzle ow rate

by the equations

mCAP

FD FF

(

)

2ρ∆

(6.40)

mCdP

FDFF

(

)

111

ρ∆

(6.41)

6.21.1 Plain-Orifice Atomizers

Measurements of discharge coefcient carried out on various orice con-

gurations over wide ranges of operating conditions indicate that the most

important parameters are Reynolds number, length/diameter ratio, injection

pressure differential, ambient gas pressure, inlet chamfer (or radius), and

cavitation.

For noncavitating ow, it is found that discharge coefcients generally

increase with an increase in Reynolds number, until a maximum value is

attained at a Reynolds number of around 7000. Beyond this point, the value

of C

remains sensibly constant at its maximum value, regardless of Reynolds

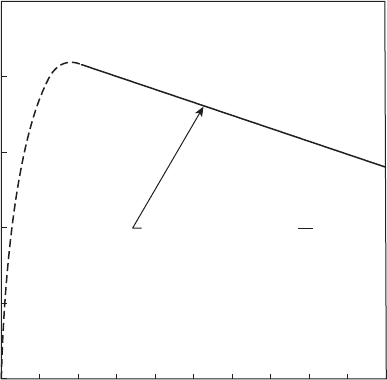
number. Maximum values of C

are shown plotted against l

in Figure 6.34.

The experimental data on which this gure is based were drawn from

Reference [75], but actual data points have been omitted for clarity. Figure 6.34

shows C

D(max)

rising steeply from about 0.61 to a maximum value of about 0.81

as l

increases from 0 to 2. Further increase in l

causes C

D(max)

to slowly

decline in a nearly linear fashion to about 0.74 at l

= 10. For the range of l

between 2 and 10, Lichtarowicz et al. [75] proposed the following expression,

which is claimed to t the experimental data to within about 1%.

Cld

D(max) oo

/=−0827 0 0085..().

(6.42)

In ow regions of low static pressure, gas or vapor may be released from

the fuel to form bubbles that can have a pronounced effect on discharge

Fuel Injection 269

coefcient. Bergwerk [76] was the rst to carry out a systematic study of cavi-

tation in plain-orice atomizers. Several others have since investigated the

inuence of cavitation on discharge coefcient. The main ndings of these

studies have been reviewed by Ohrn et al. [77]. They show that when cavita-

tion is present, C

is governed primarily by the vapor pressure of the fuel

and the pressure drop across the nozzle.

It is perhaps worthy of mention that the inuence of cavitation on injector

performance is not conned solely to its effect on discharge coefcient. For

example, Ruiz and Chigier [78] have asserted that cavitation is more impor-

tant than turbulence in promoting the initial disturbances necessary for jet

atomization, whereas Reitz and Bracco [79] claim that cavitation, although

not a necessary component for atomization, has a marked inuence when

present.

The main conclusion from the experiments of Ohrn et al. on nominally

sharp-edged inlets is that the most important factor inuencing the dis-

charge coefcient is the inlet edge condition. Examination of many scan-

ning electron microscope (SEM) photographs revealed that even minor

deviations from a sharp-edged inlet, such as roughness or a slight local

radius, could produce a signicant increase in discharge coefcient. These

workers also observed that increasing the orice inlet radius raises the dis-

charge coefcient, as noted in previous studies [76,80,81], and also causes

to increase slightly with an increase in Reynolds number up to around

30,000.

max

= 0.827–0.0085

High Reynolds number

Orifice length/diameter ratio

0.85

Maximum value of discharge coefficient

0.80

0.75

0.70

0.65

0.60

012345678910

Figure 6.34

Variation of C

D(max)

with orice l

ratio.