Lee K.K. Lectures on Dynamical Systems, Structural Stability and Their Applications
Подождите немного. Документ загружается.


by
the
differential
system
dxjdt
=
f(x,y),
dy/dt
=
af(x,y)
where
f(x,y)
=
f(x+1,y+1)
=
f(x+1,y)
=
f(x,y+1),
and
f(x,y)
> 0
if
x
and
y
are
not
both
zero,
f(O,O)
= o.
Let
a > 0
be
irrational.
It
is
clear
that
there
is
a
fixed
point
p =
(0,0).
There
is
only
one
orbit
r
1
such
that
a(r
1
)
=
(p},
and
exactly
one
orbit
r
2
such
that
n(r
2
)
=
{p}.
For
any
other
orbit
r,
a(r)
=
O(r)
=
the
torus.
Moreover,
O(r
1
)
=
a(r
2
)
=
the
torus.
It
is
also
clear
that
points
on
r
1
are
positively,
but
not
negatively,
Poisson
stable.
Likewise,
points
on
r
2
are
negatively,
but
not
positively,
Poisson
stable.
All
other
points
are
Poisson
stable.
But,
no
point
except
the
fixed
point
p
is
periodic.
The
following
theorem
sheds
some
light
on
positively
Poisson
stable
points
X when r+(X) +
O(X).
Theorem
4.3.12
Let
X
be
a
complete
metric
space.
Let
x
e X
be
positively
Poisson
stable,
and
let
it
not
be
a
periodic
point.
Then
the
set
O(X) -
r(x)
is
dense
in
n(x),
i.e.,
n~c
x_,.)--....,r~c'"""x~)
= n c x) = r c
x)
•
Corollary
4.3.13
If
X
is
complete,
then
r(x)
is
periodic
iff
r(x)
=
n(x).
This
corollary
is
closely
related
to
Corollary
4.3.9.
Now
let
us
introduce
the
definition
of
a
non-wandering
point.
A
point
x e X
is
non-wandering
if
every
neighborhood
U
of
x
is
self-positively
recursive.
We
shall
state
a
few
theorems
showing
the
connection
between
Poisson
stable
points
and
non-wandering
points.
Lemma
4.3.14
Let
X E
X.
Every
y E
O(x)
is
non-wandering.
Theorem
4.3.15
Let
P c X
such
that
every
x e P
is
either
positively
or
negatively
Poisson
stable.
Then
every
x
164

E P
is
non-
wandering.
Theorem
4.3.16
Let
X
be
complete.
Let
every
x E X
be
non-
wandering,
then
the
set
of
Poisson
stable
points
P
is
dense
in
x.
Again,
a
closely
related
theorem
is
the
following:
Theorem
4.3.17
For
any
dynamical
system~
on
X,
the
set
of
all
non-wandering
points
of~'
n(~),
is
a
closed
invariant
subset
of
X,
and
is
non-empty
if
X
is
compact.
Furthermore,
topological
conjugacies
and
equivalences
preserve
the
set
of
non-wandering
points.
Before
we
introduced
the
notion
of
non-wandering
points,
we
were
seeking
some
new
(or
additional)
equivalence
relations
with
respect
to
which
classification
might
be
made
easier.
The
new
equivalence
relation
are
called
n-eguivalence
(for
flow)
and
n-conjugacy
(for
homeomorphisms).
They
are
just
the
old
ones,
topological
equivalence
and
conjugacy,
restricted
to
n-sets.
Thus
if
~In(~)
denotes
the
restriction
of
the
flow~
ton(~),
defined
by
<~In(~))
(t,x)
=
~(t,x)
for
all
(t,x)
E R x
n(~),
then
0
is
n-
equivalent
to
u
iff
~I
nc~>
is
topologically
equivalent
to
~In(~).
Similarly,
homeomorphisms
f
and
g
are
n-conjugate
iff
their
restrictions
fln(f)
and
gln(g)
are
topologically
conjugate.
From
the
last
theorem,
topological
equivalence
(or
conjugacy)
is
stronger
than
n-equivalence
(or
conjugacy).
Earlier,
we
touched
upon
the
concept
of
a
minimal
set.
In
the
following,
we
shall
characterize
a
minimal
set
and
its
existence
theorems.
Theorem
4.3.18
A
non-empty
set
A c X
is
minimal
iff
r(x)
= A
for
every
x E A.
Theorem
4.3.19
If
A c X
is
minimal
and
the
interior
of
A
is
non-empty,
then
A=
Int(A).
Theorem
4.3.20
Let
A c X
be
non-empty
and
compact.
Then
the
following
statements
are
equivalent:
(i)
A
is
minimal,
(ii)
r(x)
= A
for
every
x E
A,
(iii)
r~(x)
= A
for
every
x E
A,
165

(iv)
n(x)
= A
for
every
x £ A,
(v)
a(x)
= A
for
every
x £ A.
A
fixed
point
and
a
periodic
orbit
are
examples
of
compact
minimal
sets.
From
the
above
theorem,
every
point
in
a
compact
minimal
set
is
Poisson
stable.
The
example
for
an
irrational
flow
on
T
2
indicates
that
the
closure
of
a
Poisson
stable
orbit
need
not
be
a
minimal
set.
This
is
because
the
closure
of
every
Poisson
stable
orbit
except
the
fixed
point
is
the
whole
torus,
which
is
not
minimal,
for
it
contains
a
fixed
point.
Birkhoff
[1927]
discovered
an
intrinsic
property
of
motions
in
a
compact
minimal
set,
which
is
usually
called
the
property
of
recurrence.
For
any
x £
X,
the
motion
~x
is
recurrent
if
for
each
£
> 0
there
exists
a T = T(E) > o,
such
that
r(x)
c
B([t-T,t+T]·x,E)
for
all
t £ R.
Since
every
motion
~Y
with
y £
r(x)
is
also
recurrent
if
~x
is
recurrent,
thus
we
shall
speak
of
the
orbit
r(x)
being
recurrent.
Moreover,
a
point
x £ X
is
recurrent
if
~x
is
recurrent.
Note
also
that
every
recurrent
motion
is
Poisson
stable.
Theorem
4.3.21
Every
orbit
in
a
compact
minimal
set
is
recurrent.
Thus
every
compact
minimal
set
is
the
closure
of
a
recurrent
orbit.
Theorem
4.3.22
If
r(x)
is
recurrent
and
r(x)
is
compact,
then
r(x)
is
also
minimal.
Corollary
4.3.23
If
X
is
complete,
then~
of
any
recurrent
orbit
is
a
compact
minimal
set.
So
far
our
discussions
were
centered
on
compact
minimal
sets,
not
much
is
known
about
the
properties
of
non-compact
minimal
sets.
It
has
been
established
that
all
minimal
sets
in
R
2
consist
of
single
orbit
with
empty
limit
sets
[Bhatia
&
Szego
1967].
Nonetheless,
usually
compact
minimal
sets
contain
more
than
one
orbit.
Lemma
4.3.24
There
exists
non-compact
minimal
sets
which
contain
more
than
one
orbit.
Consider
the
dynamical
system
of
irrational
flow
on
a
166

torus
discussed
earlier
restricting
the
system
to
the
complement
of
the
fixed
point
in
that
example.
The
resulting
space
X
is
non-
compact,
but
for
each
x e X,
r(x)
= X,
so
that
X
is
minimal.
This
proves
the
lemma.
Note
that,
in
the
above
construction,
~x
are
not
recurrent.
This
shows
that
Theorem
4.3.21
is
not
necessarily
true
for
non-compact
minimal
sets.
For
any
x e X,
the
motion
~x
is
positively
Lagrange
stable
if
r•(x)
is
compact.
If
r·(x)
is
compact,
then
the
notion
~x
is
negatively
Lagrange
stable.
It
is
Lagrange
stable
if
r(x)
is
compact.
Remark:
If
X = R",
then
the
above
statements
are
equivalent
to
the
sets
rt(x),
r(x)
being
bounded.
One
can
also
show
that
(i)
If
X
is
locally
compact,
then
a
motion
~x
is
positively
Lagrange
stable
iff
n(x)
is
a
non-empty
compact
set:
(ii)
If
~x
is
positively
Lagrange
stable,
then
n(x)
is
compact
and
connected;
(iii)
If
~x
is
positively
Lagrange
stable,
then
d(t·x,
n(x))
~
0
as
t
~
~.
Theorem
4.3.25
Every
non-empty
compact
invariant
set
contains
a
compact
minimal
set.
Theorem
4.3.26
The
space
X
contains
a
compact
minimal
set
iff
there
is
an
x e X
such
that
either
r•(x)
or
r·(x)
is
compact.
It
is
worthwhile
to
note
that
the
only
recurrent
motins
in
R
2
are
the
periodic
ones.
As
a
consequence,
all
compact
minimal
sets
in
R
2
are
the
orbits
of
periodic
points.
Indeed,
Hajek
[1968]
shows
that
all
positively
Poisson
stable
points
in
R
2
are
periodic.
Moreover,
the
only
noncompact
minimal
sets
in
R
2
consist
of
a
single
orbit
with
empty
n-limit
and
a-limit
sets
[Bhatia
and
Szego
1967].
Then
Theorem
4.3.18
implies
that
all
minimal
sets
in
R
2
have
empty
interiors.
This
theorem
also
poses
an
important
and
interesting
problem,
i.e.,
which
phase
spaces
(or
manifolds)
can
be
minimal.
A
special
case
of
recurrence,
namely
almost
periodicity,
is
deferred
to
next
chapter
because
it
is
intimately
connected
to
the
notion
of
stability
of
motion.
It
is
167

worthwhile
to
note
that
the
concepts
of
recursiveness
can
be
generalized
to
non-metric
topological
spaces,
whereas
almost
periodicity
requires
a
uniformity
on
the
space.
4.4
Velocity
fields,
integrals,
and
ordinary
differential
equations
In
this
section,
we
shall
discuss
the
existence
and
uniqueness
of
a
flow
whose
velocity
is
a
given
vector
field.
By
using
a
chart,
the
local
problem
is
equivalent
to
the
existence
and
uniqueness
of
solutions
(integral
curves)
of
a
system
of
ordinary
differential
equations.
Recall
that,
if
M
is
a
differentiable
manifold,
a
vector
field
on
M
is
a
map
X: M
~
TM
associated
with
each
point
p €
M a
vector
X(p)
in
the
tangent
space
MP.
We
can
think
of
MP
as
the
space
of
all
possible
velocities
of
a
particle
moving
along
paths
on
M
at
p.
Also
recall
that
if
X
is
a
given
vector
field
on
M,
we
call
any
flow
¢
on
M
an
integral
flow
of
X
if
X
is
the
velocity
vector
field
of
¢.
We
also
say
that
X
is
integrable
if
such
a
flow
exist.
Theorem
4.4.1
Let
¢
be
a
flow
on
M
such
that,
for
all
p
€
M,
the
map
¢p:
R
~
M
is
differentiable.
Then
the
velocity
of
¢
at
any
point
is
independent
of
time.
Thus
¢
has
a
well
defined
velocity
vector
field.
An
integral
curve
of
X
is
at
least
a c
1
map
r:
I
~
M,
where
I
is
any
real
interval
such
that
r•(t)
=
Xr(t)
for
all
t €
I.
A
local
integral
of
X
is
a
map
¢:
I x U
~
M,
where
I
is
an
interval
neighborhood
of
0
and
U
is
a
non-empty
open
subset
of
M,
such
that
for
all
p € u,
¢p:
I
~
U
is
an
integral
curve
of
X
at
p.
For
all
p €
U,
we
call
¢ a
local
integral
at
p,
and
say
that
X
is
integrable
at
p
if
such
a
local
integral
exists.
If
it
does
and
is
at
least
c
1
,
then
the
diagram
T(IxU)
y t
I
xU
168
TM
t X
M

commutes.
If
I
can
be
extended
to
R,
and
U
to
M,
then
the
local
integral
is
a
flow
on
M.
We
shall
come
back
to
this
shortly.
Theorem
4.4.2
Let
X
be
a
vector
field
on
M,
and
let
h:
M
~
N
be
a c
1
diffeomorphism.
If
r
is
an
integral
curve
of
X,
then
h
is
an
integral
curve
of
the
induced
vector
field
h.(X)
=
(Th)
Xh-
1
on
N
from
X
by
h.
If
q,:
IxU
~
M
is
a
local
integral
of
X
at
p,
then
hq,(id
x
(hiu)-
1
)
is
a
local
integral
of
h.(X)
at
h(X).
It
is
intuitively
clear
that
the
following
theorem
follows.
Theorem
4.4.3
Any
integral
curve
of
a
ck
vector
field
is
ck•
1
•
Let
V
be
an
open
subset
of
a
Banach
space
B,
and
let
X
be
a
ck
vector
field
on
V
(k
~
0).
Also
suppose
that
q,:
IxU
~
V
is
a
local
integral
of
X.
We
now
express
the
condition
that
r
be
an
integral
curve
of
X
in
terms
of
local
representatives
with
respect
to
natural
charts.
Let
(U,
~)
be
a
chart
of
M
and
suppose
the
image
of
r
is
contained
in
u.
Then
the
local
representative
of
r
with
respect
to
the
identity
of
Rand
(U,
~)
is
r~
=
~-r,
while
the
local
representative
of
the
curve
r•
with
respect
to
the
identity
of
Rand
natural
chart
(TMIU,T~)
is
given
by
(r')~(t)
=
T~-r'(t)
=
T~·Tr(t)
=
T(~-r)
(t)
=
(r~)
'(t)
by
the
composite
mapping
theorem.
Also,
the
local
representative
of
x-r
with
respect
to
the
identity
of
R
and
the
natural
chart
T~
is
Twx·r
=
Twx·~-
1
·wr
= x
·r
where
x
is
the
local
~ ~
~
representative
of
X.
Thus
r
is
an
integral
curve
of
X
iff
x·
r =
r•,
iff
X~·
r~
=
r/,
iff
r~
is
an
integral
curve
of
X~.
This
condition
takes
a
simple
and
usual
form
if
~(U)
c R".
ThenwehaveX~(p)
=
(p;X
1
(p),
.•.
,Xn(P))
wherep
e
~(U)
cR",
{X;(P)}
are
the
components
of
X~,
r~(t)
=
(r
1
(t),
...
,rn(t)),
r~'(t)
=
(r(t);
r
1
'(t),
..•
,rn'(t)),
and
x~·r~
=
r~·
iff
r~'(t)
=
X;(r(t))
fori=
l,
...
,n
and
all
t e
I.
Thus,
r
is
an
integral
curve
of
X
iff
the
local
representatives
satisfy
the
system
of
first-order
ordinary
diffeerential
equations
r
1
I (
t)
=
X1
( r
1
(
t)
1 • • • 1 r n (
t)
) 1
169

rn'
(t)
=
Xn(r,(t)
I
••
•
,rn(t)).
Note
that
t
does
not
appear
explicitly
on
the
right.
Such
a
system
of
equations
(a
local
dynamical
system)
is
called
an
autonomous
system.
It
includes
regular
equations
of
higher
order
and
the
Hamiltonian
equations
of
motion
as
special
cases.
We
should
also
point
out
that
any
m-th
order
ordinary
differential
equation
in
standard
form
d"'yjdt'" =
h(t,y,dyjdt,
••
,d'""
1
yjdt'""
1
)
1
can
be
reduced
to
the
form
dxjdt
=
g(t,x),
where
x =
(x
1
,
•••
,x,.) e
R'",
and
g
is
a
vector
valued
function.
By
substituting
x
1
=
y,
x
2
=
dyjdt,
..•
,
x,.
=
d'""
1
y/dt'""
1
,
and
g(t,x)
=
(x
2
,x
3
,
•••
,x,.,
h(t,x
1
,
•••
,x,.)).
Example:
In
Chapter
1
we
introduced
the
pendulum
equation
d'6jdt'
=
-g
sin6
and
it
was
reduced
to
d6jdt
= n,
dO/dt
=
-g
sin6
by
the
substitution
n =
d6jdt.
Example:
In
classical
mechanics,
with
a
conservative
force
field,
Lagrange's
equations
of
motion
can
be
obtained
from
the
Euler-Lagrange
equation
d/dt(aL;aq;>
-
aL;aq;
= o,
where
q;
(1
:5
i
:5
n)
are
the
"generalized
coordinates",
the
Lagrangian
L = T -
v,
where
T
is
the
kinetic
energy
and
v
is
the
potential
energy.
In
terms
of
the
generalized
coordinates,
T
1/2
:E;.,n
mi<dqi/dt>',
then
the
equations
of
motion
becomes
m;
dq;'
/dt'
-
av;aq;.
With
the
substitution
m;dq;/dt
=
P;,
the
"generalized
momentum",
converts
the
equations
of
motion
to
dp;fdt
-av;aq;.
The
generalized
coordinates
q;
and
its
time
derivatives
dq;/dt
form
the
coordinates
of
the
tangent
bundle
of
the
configuration
space
M;
while
the
generalized
coordinates
and
generalized
momenta
form
the
coordinates
of
the
cotangent
bundle
T*M
of
the
configuration
space.
In
the
T*M,
the
equations
of
motion
are
the
Hamilton's
equations
dq;Jdt
=
aH;ap;,
and
dp;fdt
= -
aH;aq;,
170
where
the
Hamiltonian
H = T + V
is
also
the
total
energy
of
the
system.
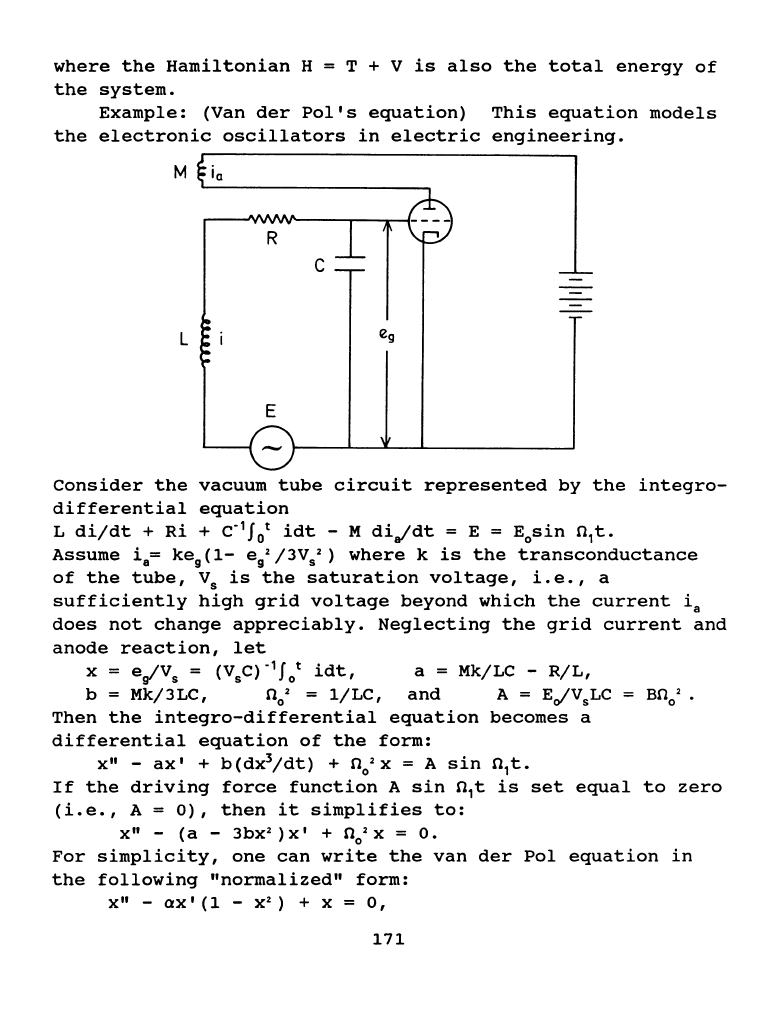
Example:
(Vander
Pol's
equation)
This
equation
models
the
electronic
oscillators
in
electric
engineering.
M i
0
~----------------~
Consider
the
vacuum
tube
circuit
represented
by
the
integra-
differential
equation
L
dijdt
+
Ri
+
C"
1
J
0
t
idt
- M
di,ldt
= E = E
0
sin
n
1
t.
Assume
i
8
=
ke
9
(1-
e
9
2
/3V
8
2
)
where
k
is
the
transconductance
of
the
tube,
V
8
is
the
saturation
voltage,
i.e.,
a
sufficiently
high
grid
voltage
beyond
which
the
current
i
8
does
not
change
appreciably.
Neglecting
the
grid
current
and
anode
reaction,
let
X =
eg/V
8
= (V
8
C)
·l
f
0
t
idt,
a = Mk/LC -
R/L,
b =
Mk/3LC,
n
0
2
=
1/LC,
and
A = EofV
8
LC
Bn
0
2
•
Then
the
integra-differential
equation
becomes
a
differential
equation
of
the
form:
x"
-
ax'
+
b(dxljdt)
+ n
0
2
x = A
sin
n
1
t.
If
the
driving
force
function
A
sin
n
1
t
is
set
equal
to
zero
(i.e.,
A=
O),
then
it
simplifies
to:
X
11
-
(a-
3bX
2
)X
1
+ n
0
2
X =
0.
For
simplicity,
one
can
write
the
van
der
Pol
equation
in
the
following
"normalized"
form:
x"-
ax'(1-
X
2
)
+ x = o,
171

where
a
is
a
positive
constant.
We
can
transform
this
second
order
equation
into
a
pair
of
first
order
equations
as
the
following,
x'
=
y,
y'
=
-x
+
ay(
1-
x•).
The
phase
portrait
of
this
vector
field
on
R
2
is
topologically
equivalent
to
the
following
figure.
It
has
a
unique
closed
orbit
which
is
the
n-set
of
all
the
orbits
except
the
fixed
point
[Hirsch
&
Smale
1974].
The
system
is
said
to
be
auto-oscillatory
since
all
(except
one)
solutions
tend
to
become
periodic
as
time
increases.
Let
p
be
a
point
of
a
Banach
space
B,
let
X
be
a
vector
field
on
some
neighborhood
U
of
p.
We
want
to
find
out
whether
for
some
neighborhood
V
of
p
there
are
unique
integral
curves
at
each
point
of
V.
In
order
to
prove
uniqueness,
we
need
something
stronger
than
continuity
and
which
is
the
Lipschitz
condition.
First
we
shall
define
a
Lipschitz
map.
Let
P
and
Q
are
non-empty
metric
spaces
with
distance
function
d.
Let
k
be
any
positive
number.
A
map
f:
P
~
Q
is
Lipschitz
(with
constant
k)
if,
for
all
p,p'€
P,
d(f(p),f(p'))
~
kd(p,p').
Clearly,
any
Lipschitz
map
is
continuous
(in
fact,
uniformly
continuous).
A
map
f
is
locally
Lipschitz
if
every
p € P
has
a
neighborhood
on
which
f
is
Lipschitz.
Clearly,
Lipschitz
condition
implies
continuity
and
it
is
satisfied
by
any
c
1
map
on
u.
Thus,
Lipschitz
condition
is
about
half
way
between
continuity
and
differentiability.
As
before,
let
p
be
a
point
of
a
Banach
space
B,
X
be
a
vector
field
on
some
neighborhood
U
of
p,
and
V
be
some
other
neighborhood
of
p.
Let
d'
and
d
are
the
distance
functions
of
U
and
V
respectively.
172

Theorem
4.4.4
(Picard)
Let
f:
U
~
B
be
Lipschitz
with
constant
k,
and
let
I
be
the
interval
[-a,a],
where
a<
(d'-d)/lfl
0
if
d'<
~,
and
lfl
0
is
the
Banach
norm.
Then
for
each
p
~
V,
there
exists
a
unique
integral
curve
~P:
I
~
U
off
at
p.
Let~:
IxV
~
U
send
(t,p)
to
~P(t).
Then
for
all
t
~I,
~t:
V
~
U
is
uniformly
Lipschitz
(in
t),
and
cr
iff
is
cr.
Theorem
4.4.5
Same
assumptions
as
in
the
above
theorem.
If
d'<
~
,
then
the
map
~
is
Lipschitz.
And
it
is
locally
Lipschitz.
This
theorem
provide
an
answer
as
to
the
dependence
of
~
on
t
and
x
together.
It
says
that
~
is
locally
Lipschitz,
and
~
is
as
smooth
as
f.
Then
the
main
theorem
on
the
smoothness
of
local
integrals
follows
easily.
Theorem
4.4.6
If
the
map
f
of
Theorem
4.4.4
is
cr
(r
~
1),
then
the
local
integral~
is
also
cr.
Furthermore,
D
1
(D
2
)r~
exists
and
equals
to
(D
2
)r(f~):
I x B
~
L
8
(B,B).
Since
any
c
1
vector
field
is
locally
Lipschitz,
we
have
the
following
useful
corrollary:
Corollary
4.4.7
Any
cr
vector
field
(r
~
1)
on
a
manifold
has
a
cr
local
integral
at
each
point
of
the
manifold.
So
far
we
have
been
dealing
with
local
integrability
condition
and
uniqueness.
The
main
tool
for
extending
local
integrability
condition
to
global
one
is
the
uniqueness
of
integral
curves
proved
earlier.
The
next
theorem
is
the
global
uniqueness
theorem.
Theorem
4.4.8
Let
X
be
a
locally
Lipschitz
vector
field
on
a
manifold
M,
and
let
a:
I
~
M,
and
p:
I
~
M
be
integral
curves
of
X.
If
for
some
t
0
~I,
a(t
0
)
=
P(t
0
),
then
a=
P
Recall
that
a
point
p
~
M
is
a
singular
point
of
a
vector
field
X
if
X(p)
=
o.
One
can
easily
show
that
all
integral
curves
of
a
locally
Lipschitz
vector
field
X
at
p
are
constant
functions
if
p
is
a
singular
point
of
x.
Earlier
we
commented
that
if
the
velocity
of
a
flow
is
independent
of
time,
we
may
consider
such
a
flow
as
a
vector
field.
conversely,
the
following
theorem
states
that
a
local
173
