Лазоренко О.В., Черногор Л.Ф. Нелинейная радиофизика. Сборник задач
Подождите немного. Документ загружается.

Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.2. Примеры
60
2
1
dy
dt
y
=
−λ
−
.
Откуда
()
(
)
th
y
tCt=−λ. При t = ∞ x(∞) = th(–∞)=–1, где С – любое конечное число.
Положим С = 0. Тогда:
22
th
y
t=λ, а
(
)
222
000
th
A
tA t
=
λ
. В конечном счете
()
()
1,2 1,2
22222
1,2 00 0 00
00
ch
A
tAAA t
−
γγ
=−= λ
γγ
– “светлый” солитон,
(
)
(
)
22 2
000
1
A
tA cht
−
=−λ
– “темный” солитон.
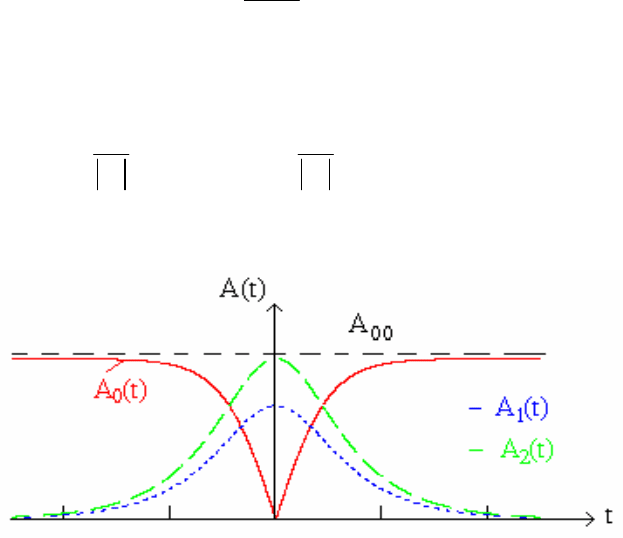
Рис. 5.3. Вид решений А
0,1,2
(t)
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.3. Задачи для самостоятельного решения
61
5.3. Задачи для самостоятельного решения
5.1
Решить задачу о двухволновом взаимодействии, если оно описывается системой вида:
а)
()
1
112 1 1
0
2
201 2
0
,0,
,0;
t
t
dA
AA A A
dt
dA
AA A
dt
=
=
=−γ =
=γ =
б)
()
2
1
12 1
0
2
212 2 2
0
,0,
,0;
t
t
dA
AA
dt
dA
AA A A
dt
=
=
=γ =
=−γ =
в)
()
1
112 1 1
0
2
2
21 2
0
,0,
,0;
t
t
dA
AA A A
dt
dA
AA
dt
=
=
=−γ =
=
γ=
г)
()
1
12 1 1
0
2
21 2
0
,0;
,0.
t
t
dA
AAA
dt
dA
AA
dt
=
=
=−γ =
=γ =
Учесть, что
12
,0γγ>.
5.2
Вычислить пороговое значение амплитуды волны накачки в задаче о трехволновом
когерентном взаимодействии (γ
1,2
> 0; γ
0
< 0):
a)
2
1
10 2 11
2
2
201 2 2
2
0
01 2 00
,
,
;
dA
AA A
dt
dA
AA A
dt
dA
AA A
dt
=γ −ν
=γ −ν
=γ −ν
б)
2
1
10 2 110
2
2
210 220
22
0
01 2 00
,
,
;
dA
AA AA
dt
dA
AA A A
dt
dA
AA A
dt
=γ −ν
=γ −ν
=−γ −ν
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.3. Задачи для самостоятельного решения
62
в)
2
1
1012 11
2
2
2012 22
2
0
0012 00
,
,
;
dA
AAA A
dt
dA
AAA A
dt
dA
AAA A
dt
=γ −ν
=γ −ν
=−γ −ν
г)
3
1
10 2 11
3
2
210 2 2
2
0
012 0 00
,
,
.
dA
AA A
dt
dA
AA A
dt
dA
AAA A
dt
=γ −ν
=γ −ν
=−γ −ν
Начальные условия имеют вид:
12000
000
0, 0, .
ttt
A
AAA
===
===
5.3
Исследовать взрывную неустойчивость, описываемую уравнением
а)
3
dA
AA
dt
=
γ−ν,
б)
32
,
dA
A
A
dt
=
γ−ν
в)
324
,
dA
A
AA
dt
=
γ−ν−β
г)
42
,
dA
A
A
dt
=
γ−ν
где
,0,νγ>
(
)
()
0
0
A
A>
, А
(0)
– пороговoе значение.
5.4
В результате трехволнового взаимодействия могут возникать солитоны огибающих. Они
описываются следующей моделью:
1
102
2
201
0
012
,
,
,
dA
AA
dt
dA
AA
dt
dA
AA
dt
⎧
=γ
⎪
⎪
⎪
=γ
⎨
⎪
⎪
=γ
⎪
⎩
где
() ()
12 0 1,2 0 00
,0, 0, 0, ,
г
x
A
tt A A
′
γγ> γ< ±∞= = − ±∞=
v
, v
г
– групповая скорость.
Отыскать А
1
(t), А
2
(t), А
0
(t).
Указание. Использовать соотношения Мэнли – Роу
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.3. Задачи для самостоятельного решения
63
5.5
Известно, что ребенок интенсивно растет до 12 – 13 лет: его масса в начале жизни
увеличивается в e раз примерно за 2,6 года. Считая, что относительная скорость увеличения
массы ребенка уменьшается по экспоненциальному закону с характерным временем, равным 8
годам, составить уравнение, описывающее закон изменения массы человека в течение жизни.
Найти его решение и постройте зависимость
m(t). Относится ли такое поведение к
неустойчивости? Если да, то какого типа? Принять m(0) = 3,5 кг.
5.6
Скорость роста численности N простейших организмов в биосфере пропорциональна их
числу. Это же можно сказать и о скорости их гибели. Составить дифференциальное уравнение,
описывающее изменение N во времени. Получить его решение. Описывает ли оно
неустойчивость? При каких условиях? Привести примеры.
5.7
Скорость роста численности N сложных организмов в биосфере пропорциональна
квадрату их числа, а скорость гибели – N. Составить дифференциальное уравнение,
описывающее изменение N во времени. Получить его решение. Описывает ли оно
неустойчивость? Какую? При каких условиях? Привести примеры.
5.8
Численность N многих организмов в биосфере описывается логистическим законом,
согласно которому относительная скорость изменения N во времени убывает с ростом N по
линейному закону. Составить дифференциальное уравнение, описывающее изменение N во
времени. Получить его решение. Описывает ли оно неустойчивость? Какую? При каких
условиях? Привести примеры.
5.9
В некоторую историческую эпоху, которая включает в себя и настоящее время, рост
численности населения на Земном шаре хорошо описывается простейшей моделью С. П.
Капицы:
2
dN N
dt C
= ,
где С ≈ 1,86⋅10
11
чел⋅год.
Является ли такой рост устойчивым? Найдите и проанализируйте зависимость N(t). В
каком году наступит “взрыв” численности населения, если в 1999 г. N = 6 млрд человек?
Реальна ли модель С. П. Капицы? Чего она не учитывает? Попытайтесь усовершенствовать эту
модель.
5.10
В некоторую историческую эпоху, которая включает в себя и настоящее время, рост
численности населения на Земном шаре хорошо описывается усовершенствованной моделью С.
П. Капицы:
22
0
()
dN C
dt t
=
τ
−+τ
,
где С ≈ 1,86⋅10
11
чел⋅год, τ ≈ 42 года – характерное время для человека, τ
0
≈ 2007 год.
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.3. Задачи для самостоятельного решения
64
Является ли такой рост устойчивым? Найдите и проанализируйте зависимость N(t). В
каком году наступит стабилизация численности населения, если в 1999 г. N = 6 млрд человек?
Реальна ли эта модель С. П. Капицы? Вычислите N в текущем году и сравните его с
результатами
переписи населения. Существенны ли отклонения от модели?
5.11
Рост потребляемой человечеством мощности описывается моделью вида:
()
dP
PP
dt
=α
, P|
t = 0
= P
0
,
где P
0
= 20 ТВт,
0
(1 )Pα=α +β , α
0
≈ 0,03 год
–1
,
14
||10β
−
≈ Вт
–1
. Найдите и проанализируйте
решение модельного уравнения. Описывает ли оно неустойчивость? Какую? При каких
условиях?
5.12
Рост мощности электромагнитного излучения, “загрязняющего” радиоэфир описывается
моделью вида:
2
(1 )
dP
PP
dt
=α +β +γ
, P|
t = 0
= P
0
,
где P
0
= 10 ГВт, α = 0,1 год
–1
,
12
||10
−
β≈ Вт
–1
,
21
||10
−
γ≈ Вт
–2
. Найдите и проанализируйте
решение модельного уравнения. Описывает ли оно неустойчивость? Какую? При каких
условиях?
5.13
Рост численности фрагментов космического “мусора” на околоземных орбитах
описывается моделью вида:
()
dn
nn n
dt
=α −β , n|
t = 2000 год
= n
0
,
где, n
0
= 10
4
,
01
nα=α +α
, α
0
≈ 0,05 год
–1
, α
1
≈ 10
–7
год
–1
, β = 0,02 год
–1
. Найдите и
проанализируйте решения модельного уравнения. Описывает ли оно неустойчивость? Какую?
При каких условиях? Через сколько лет полеты в околоземном космосе станут невозможными?

Глава 6. Нелинейные эффекты в плазме
6.1. Основные понятия и соотношения
65
6. НЕЛИНЕЙНЫЕ ЭФФЕКТЫ В ПЛАЗМЕ
6.1. Основные понятия и соотношения
Плазмой называется полностью или частично ионизированный газ, который в среднем
является квазинейтральным. Нелинейные эффекты при распространении сильных
электромагнитных волн в плазме связаны с нагревом электронов и тяжелых частиц
(значительно меньшим), выталкиванием электронов в неоднородном поле (электрострикцией),
ионизацией (пробоем) газа и нелинейностью силы Лоренца. Им соответствует нагревный
(тепловой), стрикционный, ионизационный и
магнитный или же релятивистский механизмы
нелинейности. Последний обычно малосущественный, ионизационный механизм проявляется в
очень сильных полях. Поэтому чаще всего ограничиваются рассмотрением теплового и
стрикционного механизмов. Первый из них является главным в столкновительной плазме,
второй – в бесстолкновительной плазме. Механизмы становятся существенными, если
амплитуда электрического поля E
0
≥
Ε
p
,
Ε
с
, где
()
22
1
00 0
2
2
3
,
e
p
kT m
E
e
⎛⎞
δω+ν
⎜⎟
=
⎜⎟
⎝⎠
()
1
22
2
00
2
4
,
e
c
kT m
E
e
⎛⎞
ω+ν
⎜⎟
=
⎜⎟
⎝⎠
– плазменное и стрикционное поля. Здесь Т
е0
, ν
0
– температура и частота соударений
электронов (индекс “0” относится к невозмущенным условиям), e и m – заряд и масса
электрона,
43
0
~10 10
−−
δ−
– параметр столкновений, k – постоянная Больцмана, 2
f
ω
=π –
круговая частота волны.
Относительная комплексная диэлектрическая проницаемость
ε
и ее действительная
часть для изотропной плазмы равны:
()
2
1,
p
i
ω
ε= −
ωω−ν
2
22
1,
p
ω
ε= −
ω
+ν
где
1
2
2
0
p
eN
m
⎛⎞
ω=
⎜⎟
ε
⎝⎠
– плазменная частота электронов, N – их концентрация,
0
ε
–
диэлектрическая постоянная вакуума.
Для показателей преломления и поглощения справедливы следующие соотношения:

Глава 6. Нелинейные эффекты в плазме
6.1. Основные понятия и соотношения
66
1
2
2
22
1,
p
n
⎛⎞
ω
=ε= −
⎜⎟
⎜⎟
ω+ν
⎝⎠
()
2
22
.
2
p
n
ων
κ=
ωω+ν
В стационарном случае возмущенные значения Т
е
(в результате нагрева электронов) и N
(за счет электрострикции) приближенно равны:
2
0
0
2
1,
ee
p
E
TT
E
⎛⎞
=+
⎜⎟
⎜⎟
⎝⎠
2
0
0
2
exp .
c
E
NN
E
⎛⎞
=−
⎜⎟
⎝⎠
В слабо и сильно ионозированной плазме справедливы следующие зависимости:
1
2
0
,
e
T
T
∞
⎛⎞
ν=ν
⎜⎟
⎝⎠
3
2
0
.
e
T
T
−
∞
⎛⎞
ν=ν
⎜⎟
⎝⎠
В системе СИ соотношение, связывающее плотность потока энергии q и напряженность
поля, имеет равен:
2
,
240
PE
q
S
==
π
где P и S – мощность и сечение пучка. При изотропном излучении
2
4,SR=π где
R
–
расстояние от излучателя.
Глава 6. Нелинейные эффекты в плазме
6.2. Примеры
67
6.2. Примеры
Пример 1
Для теплового самовоздействия пучка в столкновительной плазме с частотой
соударений
()
1
2
00
/
ee
TTν=ν
оценить величины критического поля Е
кр
, критической мощности
Р
кр
, при которых наступает эффект самоканалирования, а также фокусное расстояние R
ф
.
Принять, что:
9
0
310
p
f =⋅ Гц,
10
10f = Гц,
91
0
310 c
−
ν=⋅ c
–1
, r
0
3
=
см,
()
22
0
1/
ee p
TT EE=+
, где
Е
р
– плазменное поле,
3
0
210
−
δ= ⋅ , r
0
– толщина пучка.
Решение
Условие самоканалирования имеет вид:
22
0
12
~, .
нл
л
k
kr
ε
π
=
ελ
Определим последовательно
,,
л
нл p
E
ε
ε
. Сначала, подставляя в выражение для
л
ε
числовые значения параметров, убедимся, что
22
00
22 2
0
111.
pp
л
ωω
ε=− ≈− ≈
ω+ν ω
Так как
нл л
ε=ε−ε, то
()
()()
()
22
222 222
00
22
2
00 00
00
0
4442
22 22
0
1
e
p
pp
p
e
нл
p
T
T
E
E
⎛⎞
ων −
⎜⎟
ων−ν ων−ν
ων
⎝⎠
ε= ≈ = =
ωωω
ω+ν ω+ν
Вычислим
E
p
2
:
(
)
22
2
00 0
26
2
3
B
310 ;
м
e
p
kT m
E
e
δω+ν
⎛⎞
=≈⋅
⎜⎟
⎝⎠
тогда
3
B
1, 7 10 .
м
p
E
⎛⎞
≈⋅
⎜⎟
⎝⎠
Из условия самоканалирования имеем:
22 2
00
4222
0
1
~.
p кр
p
E
E
kr
ων
⋅
ω
После подстановки числовых значений получаем
4
2
2
B
~10 ,
м
~10 Вт,
240
~.
кpp
кp
кp
л
фкр
нл
нл
EE
ES
P
a
Ra
⎛⎞
≈
⎜⎟
⎝⎠
≈
π
ε
≈
ε
ε
Глава 6. Нелинейные эффекты в плазме
6.2. Примеры
68
С другой стороны
2
2
0
0
2
~20см.
фкр
r
Rkr
π
=≈
λ
Пример 2
Полагая, что в результате нагрева высокочастотным (ω
>>
ν) электромагнитным полем
коэффициент поглощения волны изменяется по закону
0
2
,
1
α=α
+
θ
где
0
e
e
T
T
θ=
дается уравнением
2
2
1
p
E
E
θ= +
,
а
Е
р
– плазменное поле, получить выражение для амплитуды и множителя самовоздействия как
функции пройденного расстояния. Проанализировать их поведение в глубине плазмы, а также
для случая очень сильной волны на границе плазмы.
Решение
Переходя от укороченного уравнения для амплитуда волны Е к ее интенсивности Е
2
,
имеем
2
2
2
dE
E
dx
=
−α
или
2
2
2
2.
1
dE
E
dx
=− α
+θ
Введем
22
/
p
y
EE=
и исключим 1
y
θ
=+ из уравнения для y:
0
4.
2
dy y
dx y
=− α
+
Решение этого уравнения имеет вид:
0
4
2
.
x
y
ye Ce
−α
=
Из граничного условия при
x=0, E=E(0) следует, что y=y
0
, где
22
0
(0) / .
p
y
EE= Тогда
00
4
22
000
;.
yk
y
y
eyee k x
−
=
=α
При
0
41k >> имеет место 0y → , а значит
0
00 0
1
42
22
2
00
,.
y
yk k
yyee yyee
−−
≈≈
Отсюда
() ()
()
()
()
22
22
0
00
44
0, .
p
p
EE
EE
k
Ex E e e P x e
−
∞
≈⋅ ≈
Легко видеть, что 1
P
∞
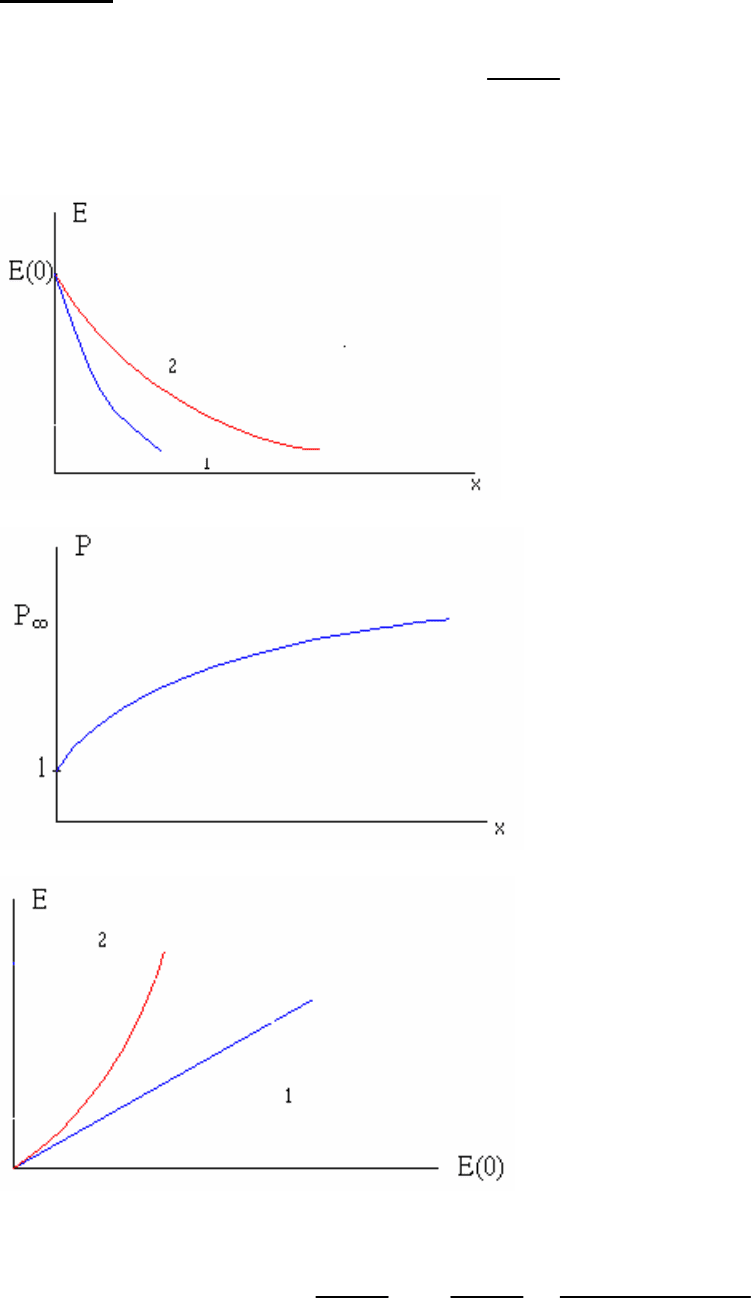
> , т. е. имеет место эффект самопросветления плазмы. При
()
22
0
p
E
E>>
имеем 1.P
∞
>> В нелинейной теории
(
)
E
t
уменьшается с ростом x медленнее,
чем в линейной.
Глава 6. Нелинейные эффекты в плазме
6.2. Примеры
69
Пример 3
Диэлектрическая проницаемость плазмы с соударениями равна:
2
0
22
1,
p
ω
ε= −
ω
+ν
где ν
=ν(T
e
) – частота соударений, T
e
– температура электронов. Определить, при каком
соотношении между ν и ν
0
=ν(T
e0
) имеет место эффект самофокусировки электромагнитного
пучка.
Рис. 6.1. Зависимость Е от x: 1 – в линейной
теории, 2 – в нелинейной.
Рис. 6.2. Зависимость P от x.
Рис. 6.3. Зависимость Е от E(0): 1 – в
линейной теории, 2 – в нелинейной
Решение
Самофокусировка имеет место при 0
нл
ε
> . Вычислим
нл л
ε
=ε−ε :
(
)
()()
222
22
00
00
22 22
22 22
0
0
11
p
pp
нл
ων−ν
⎛⎞
ωω
ε=− − − =
⎜⎟
⎜⎟
ω+ν ω+ν
ω
+ν ⋅ ω +ν
⎝⎠
.
