Лазоренко О.В., Черногор Л.Ф. Нелинейная радиофизика. Сборник задач
Подождите немного. Документ загружается.

Глава 4. Солитоны
4.2. Примеры
50
0.0998752
-0.0998752
vp1( )x
vp2( )x
100
-100 x
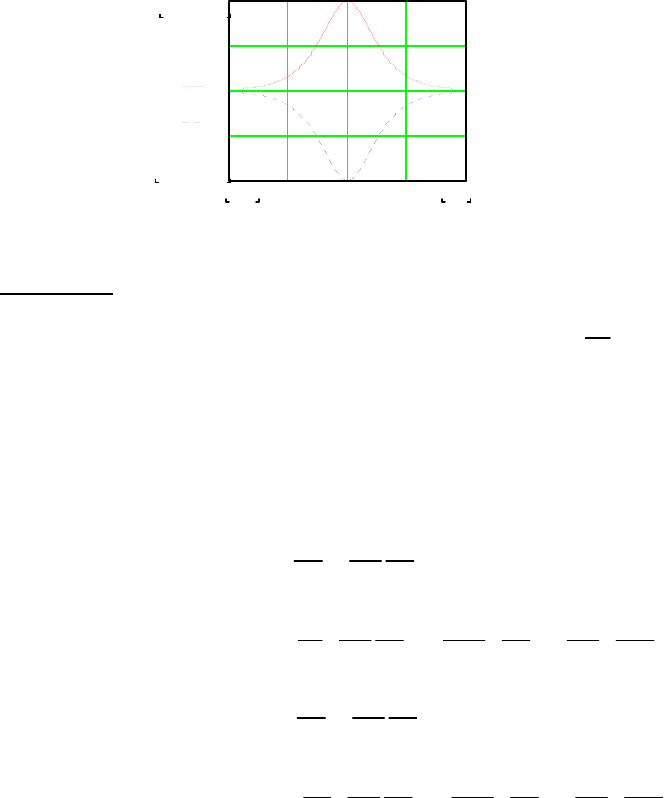
Рис. 4.2. Вид
()
±
′
ξ
v .
Пример 2
Показать, что решение в виде
()
2
0
0
chv
−
ξ
ξ=
ξ
v
также удовлетворяет линейному
уравнению гиперболического типа
2
0, .
tt xx
uxut
−
=ξ=−vv (4.9)
Решение
Докажем, что всякая функция v = v(ξ), где ξ = x – ut, есть решением такого линейного
уравнения.
22
2
22
22
22
,
,
,
t
tt
x
xx
d
u
td t
dd d
u
td t d t d t
d
xd x
dd d
xd x d x d x
∂∂ξ
′
≡= =−
∂ξ∂
⎛⎞
⎛⎞
∂∂ξ ∂ξ ∂ξ
⎛⎞
′′
==+=
⎜⎟
⎜⎟
⎜⎟
∂ξ∂ ξ∂ ξ∂
⎝⎠
⎝⎠
⎝⎠
∂∂ξ
′
≡= =
∂ξ∂
⎛⎞
⎛⎞
∂∂ξ ∂ξ ∂ξ
⎛⎞
′
′
==+=
⎜⎟
⎜⎟
⎜⎟
∂ξ∂ ξ∂ ξ∂
⎝⎠
⎝⎠
⎝⎠
vv
vv
vvv
vv
vv
vv
vvv
vv.
Подставим вычисленные производные в (4.9). Видно, что (4.9) обращается в тождество
вне зависимости от конкретного вида функции v(
ξ). Следовательно, любая v(ξ), в том числе и
заданного вида, является решением уравнения (4.9).
Глава 4. Солитоны
4.3. Задачи для самостоятельного решения
51
4.3. Задачи для самостоятельного решения
4.1
Найти солитоноподобное решение модифицированного уравнения КдВ (мКдВ)
() () ()
2
60,0,0,
0,
),
),0.
txxxx
axut
б xutu
+α +β = α> β>
′′′
±∞ = ±∞ = ±∞ =
ξ= −
ξ= + <
vvvv
vv v
4.2
Оценить амплитуду v
0
и ширину ξ
0
солитона, не решая уравнения мКдВ
() () ()
2
60,0,0;
0.
t x xxx
+α +β = α> β>
′′′
±∞ = ±∞ = ±∞ =
vvvv
vv v
Сравнить с точным решением. Принять
),
).
axut
б xut
ξ
=−
ξ
=+
4.3
Оценить амплитуду v
0
и ширину ξ
0
солитона, не решая уравнения КдВ
() () ()
0, 0, 0;
0.
t x xxx
++β= α>β>
′′′
±∞ = ±∞ = ±∞ =
vvv v
vv v
Сравнить с точным решением. Принять
),
).
axut
б xut
ξ
=−
ξ
=+
4.4
Показать, что решение в виде солитона огибающей
()
1
0
0
ch
−
ξ
ξ=
ξ
vv
также
удовлетворяет линейному уравнению гиперболического типа:
2
0.
tt xx
u
−
=vv
Принять
),
).
axut
б xut
ξ
=−
ξ
=+
4.5
Найти солитоноподобное решение уравнения Гордона типа:
() ()
3
2,
0.
tt xx
+=
′
±
∞= ±∞=
vv v
vv
Принять
Глава 4. Солитоны
4.3. Задачи для самостоятельного решения
52
),
).
axut
б xut
ξ
=−
ξ
=+
4.6
Найти и проанализировать решение нелинейного уравнения Шредингера вида:
2
0,
txx
i
+
+β =vv vv
(
)
(
)
112 2
0, 0,
,.
xut xut
′
±
∞= ±∞= β>
ξ= + ξ= +
vv
4.7
Показать, что уравнение
3
0
2,
txxx
D+=+α−βvvv v v v
0
, , , const,Dαβ =v 0
α
> , 0
β
> , 0D >
с граничными условиями
(
)
(
)
0
′
±∞ = ±∞ =vv
описывает диссипативный солитон.
4.8
Показать, что уравнение мКдВ сводится к уравнению КдВ подстановкой
2
=wv.
4.9
Найти солитоноподобное решение уравнения с нулевыми условиями на функцию ()
ξ
v и
ее первые две производные при
ξ=±∞:
а) 0,
txxxt
+
+β =vvv v
0,
β
<
б) 0,
txxtt
+
+β =vvv v
0,
β
>
в) 0,
t x ttt
+
+β =vvv v
0,
β
<
г) 0,
x t ttt
+
+β =vvv v
0.
β
>
4.10
Найти солитоноподобное решение уравнения с нулевыми условиями на функцию ()
ξ
v и
ее первые три производные при
ξ=±∞:
а)
2
() 0,
2
tt xx xxxx
α
−+ +β =vv v
0
α
> , 0
β
> ,
б)
2
() 0,
2
tt xt xxxx
α
++β=vv v
0
α
> ,
0
β
<
,
в)
2
() 0,
2
xx tt xxxx
α
++β=vvv
0
α
< , 0
β
< ,
г)
2
() 0,
2
xt tt xxxx
α
++β=vvv
0
α
> , 0
β
> .
4.11
Найти солитоноподобное решение уравнения с нулевыми условиями на функцию ()
ξ
v и
ее первые три производные при ξ=±∞:
Глава 4. Солитоны
4.3. Задачи для самостоятельного решения
53
а)
2
() 0,
2
tt xx xxxt
α
++β=vv v
0
α
< , 0
β
> ,
б)
2
() 0,
2
tt xx xxtt
α
++β=vv v
0
α
< ,
0
β
<
,
в)
2
() 0,
2
tt xx xttt
α
++β=vv v
0
α
< , 0
β
> ,
г)
2
() 0,
2
tt xx tttt
α
++β=vv v
0
α
< , 0
β
< .
4.12
Выяснить, имеет ли солитоноподобное решение уравнение КдВ с нулевыми условиями
на функцию
()ξv и ее первые две производные при ,
ξ
=±∞ если 0
β
< :
а) 0,
txxxx
+
+β =vvv v
б)
2
0.
t x xxx
+
α+β=vvvv
Сравнить полученное решение с решением для 0.
β
>
4.13
Показать, что уравнения
а) 0,
txxxxx
+α + +β =vvvvv 0,
β
>
б) 0,
ttxxxx
+α + +β =vvvvv 0
β
>
сводятся к уравнению КдВ. Найти их решения. Какие условия налагаются на
α
?

Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.1. Основные понятия и соотношения
54
5. КОГЕРЕНТНОЕ ВЗАИМОДЕЙСТВИЕ ВОЛН.
НЕУСТОЙЧИВОСТИ
5.1. Основные понятия и соотношения
Когерентное взаимодействие волн возникает благодаря передаче энергии волны
накачки с амплитудой
А
0
другим волнам. Посредником во взаимодействии выступает среда.
Рассмотрим
трехволновое взаимодействие, описываемое системой уравнений:
1
102 11,
2
201 22
0
012 0 0
,(5.1)
, (5.2)
.(5.3)
dA
AA A
dt
dA
AA A
dt
dA
AA A
dt
⎧
=γ −ν
⎪
⎪
⎪
=γ −ν
⎨
⎪
⎪
=γ −ν
⎪
⎩
Здесь
A
1
и
A
2
– амплитуды возбуждаемых волн.
Пороговое значение амплитуды волны накачки находится из (5.1) и (5.2) при
d
dt
= 0 и
равно:
(0)
12
0
12
A
ν
ν
=
γγ
.
Если потери в системе отсутствуют, т. е. ν
1
=ν
2
=ν
0
=0, то процесс взаимодействия
является
беспороговым (
(0)
0
0A = ).
Если
AA
12 0,
<<
,то применим несамосогласованный подход. При этом достаточно
решения уравнений (5.1) и (5.2). Задача сводится к
двухволновому взаимодействию.
Когерентное взаимодействие может привести к экспоненциальному росту
1,2
()At, т. е. к
генерации
неустойчивости. Она имеет стадии: линейную, когда At
0
() уменьшается
незначительно, а
1,2
()
A
t растут экспоненциально с инкрементом λ; нелинейную, когда
экспоненциальный рост
1,2
()At прекращается и
1,2 1 , 2
()At A
∞
∞
→ в результате истощения энергии
волны накачки.
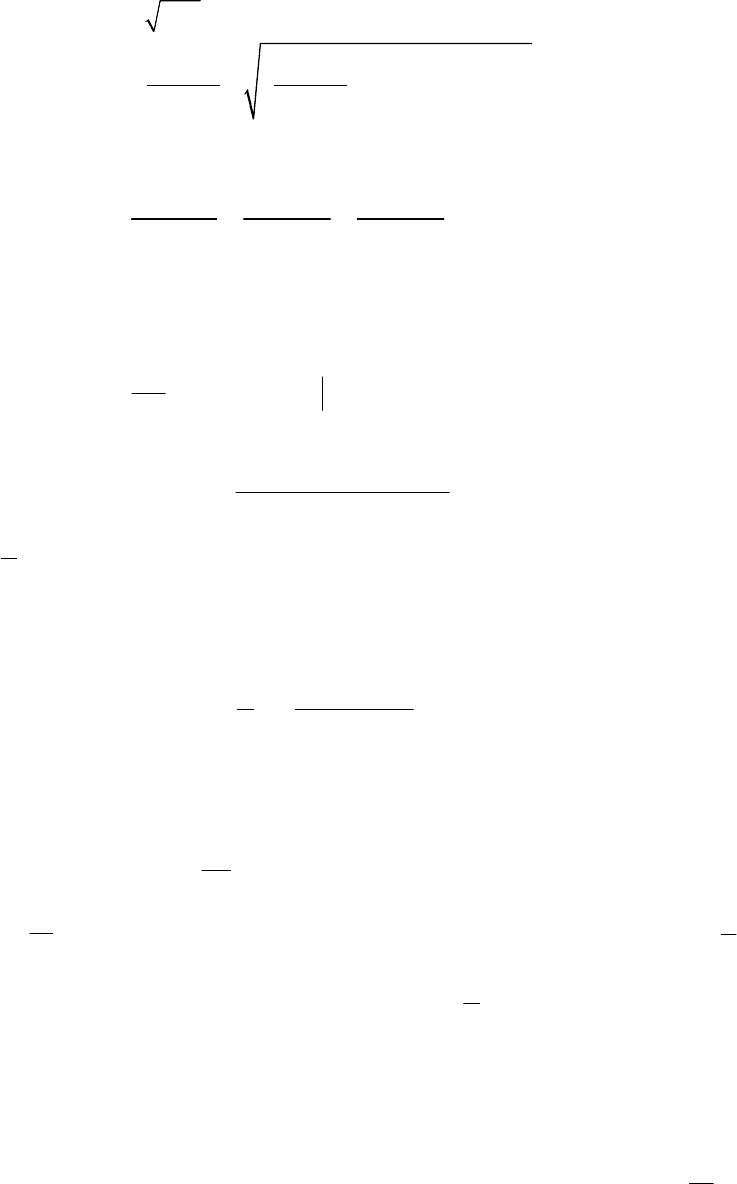
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.1. Основные понятия и соотношения
55
В отсутствие потерь
12 0
Aλ= γγ , а при их наличии:
2
2
12 12
012 12
22
A
ν+ν ν+ν
⎛⎞
λ=− + + γγ −νν
⎜⎟
⎝⎠
.
В системе без потерь справедливы
соотношения Мэнли – Роу, являющиеся
разновидностью закона сохранения энергии:
22 22 22
110 220 000
120
const,
AA AA AA−−−
===
γγγ
(5.4)
где
01,2
0, 0.γ< γ >
Взрывная неустойчивость возникает, когда приток энергии растет быстрее, чем ее
потери. Она описывается, например, таким уравнением:
()
2
0
;0,0,0.
t
dA
AAA A
dt
=
=γ −ν = γ> ν>
(5.5)
Тогда
(0)
(0)
(0)
() ,
(0) ( (0))
t
AA
At
AAAe
ν
=
+−
где
()
0
A
ν
=
γ
– значение порога. При
А(0)<A
(0)
и νt >>1 имеем
()
0At → . Если же
А(0)>A
(0)
, то наступает момент t
0
, при котором
(
)
At
0
→∞
(генерируется взрывная
неустойчивость). Для модели (5.5) справедливо выражение:
()
()
()
0
0
0
1
ln .
0
A
t
AA
⎛⎞
=
⎜⎟
⎜⎟
ν
−
⎝⎠
Реально взрывная неустойчивость ограничивается появлением дополнительного
источника потерь, который был несущественным при достаточно малых временах. Нелинейная
стадия таких неустойчивостей описывается, например, таким уравнением:
23
,0
dA
AAA
dt
=
γ−ν−β β>. (5.6)
Из (5.6) при
d
dt
= 0 следуют три решения: А
0
=0 (тривиальное, волны нет),
1
A
A
∞
γ
≈
≡
β
–
стационарное (максимальное) значение амплитуды,
()
0
2
A
A
ν
≈≡
γ
– пороговое значение
(считается, что
2
4βν << γ ). Время выхода А(t) на значение, близкое к A
∞
, равно
(
)
1
2
tA
−
∞∞
=β . (5.7)
При изучении неустойчивостей под переменной
t понимается не обязательно время, ею
может быть координата , а также время в подвижной системе координат
г
x
tt
′
=−
v
, где v
г
–
групповая скорость волнового пакета.
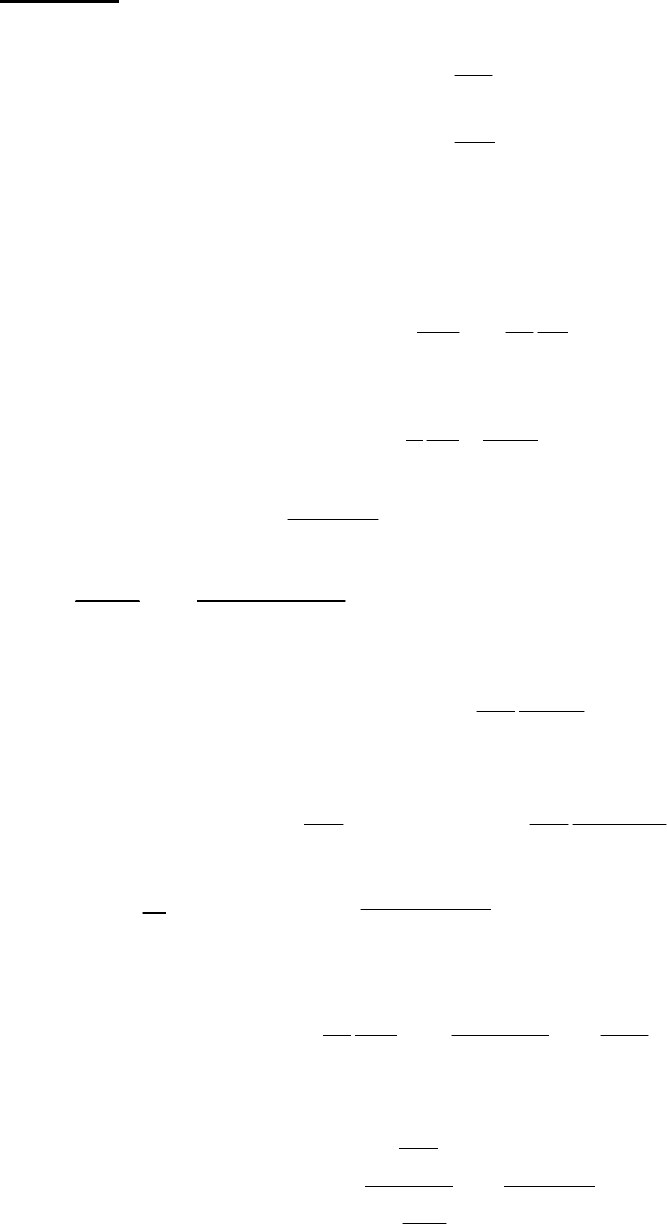
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.2. Примеры
56
5.2. Примеры
Пример 1
Решить следующую задачу о двухволновом взаимодействии:
1
102 1 0
;|0,
t
dA
AA A
dt
=
=
γ=
(5.8)
()
2
212 2 0 2
;| 0
t
dA
AA A A
dt
=
=−γ =
. (5.9)
Считать,
1,2
0γ>. Получить и проанализировать соотношение Мэнли – Роу, а также
выражения для
A
1
(t) и A
2
(t).
Решение
Разделим (5.8) на (5.9) и получим
0
11
221
.
A
dA
dA A
γ
=−
γ
Отсюда
2
02
1
12
1
.
2
AA
A
C
+
=
γγ
Из начальных условий
()
02
2
0
.
AA
C =
γγ
Тогда
() () ()
2
122
0
12
0
.
2
A
tAAt
A
−
=
γγ
Это уравнение представляет собой соотношение Мэнли-Роу. Отсюда
()
(
)
()
2
1
2
22
10
0.
2
At
At A
A
γ
=− +
γ
(5.10)
Подставим (5.10) в (5.8):
()
()
2
121
102
102
01 .
20
dA A
AA
dt A A
⎛⎞
γ
=γ −
⎜⎟
⎜⎟
γ
⎝⎠
Пусть
0.
d
dt
= Тогда
(
)
12 0
2
1
2
20
A
A
A
∞
γ
=
γ
.
Уравнение для
12
/
A
A
примет вид:
(
)
2
02
11
1
2
111
0
1.
AA
AA
d
dt A A A
∞∞ ∞
⎛⎞
=γ −
⎜⎟
⎝⎠
Разделим переменные:
()
1
02
1
1
2
1
1
2
1
0
1
A
d
AA
A
dt
A
A
A
∞
∞
∞
⎛⎞
⎜⎟
⎝⎠
=γ
−
,
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.2. Примеры
57
отсюда
()
(
)
02
111 1
1
0
,
AA t
A
tAth C
A
∞
∞
⎛⎞
=γ +
⎜⎟
⎝⎠
1
0
102
.
(0)
A
t
AA
∞
=
γ
Из начальных условий:
()
111
0th()0,AAC
∞
=
= что дает С
1
= 0.
Таким образом
()
11
0
th ,
t
At A
t
∞
=
() ( )
2
22
0
0ch .
t
At A
t
−
=
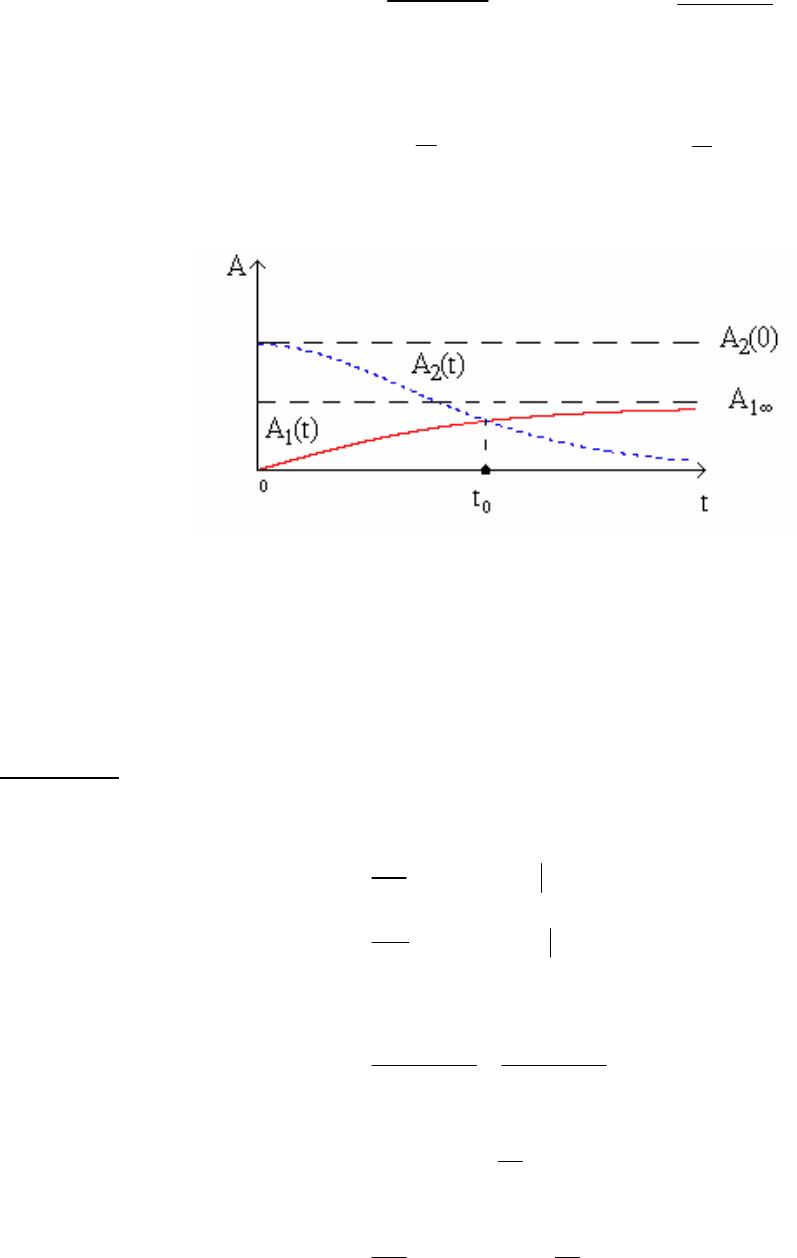
Графики решений
1
()At и
2
()At показаны на рис. 5.1.
Рис. 5.1. Вид решений
А
1
(t), A
2
(t).
Легко убедиться, что время развития неустойчивости равно
t
0
.
Энергия одной волны передается другой волне. Такое возможно только в случае, если
среда была изменена волной накачки с амплитудой
A
0
0
≠
. При А
0
= 0 никакого
взаимодействия не будет.
Пример 2
Исследовать генерацию второй гармоники в нелинейной среде, описываемую системой
укороченных уравнений:
2
1
12 1 1 1 1
0
2
2
21 2 2 2 2
0
,(0),0,
,(0),0.
x
x
dA
AA A A
dx
dA
AA A A
dx
=
=
=γ = γ <
=
γ=γ>
(5.11)
Решение
Соотношения Мэнли – Роу в данном случае имеют вид
22 22
11 22
12
(0) (0)
.
AA AA−−
=
γγ
(5.12)
Отсюда
22 22
2
22 11
1
(0) ( (0))AA AA
γ
=+ −
γ
. (5.13)
Подставляя (5.13) в (5.11), получим
222
12
11 2 1 1
1
( (0) ( (0))).
dA
AA A A
dx
γ
=γ + −
γ
(5.14)

Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.2. Примеры
58
При
x
→∞ или 0
d
dx
= справедливо такое решение для
11
()AA
∞
∞
≡ :
22 2
1
11 2
2
(0) (0)AA A
∞
γ
=−
γ
. (5.15)
С учетом (5.15) уравнение (5.14) принимает вид:
22
1
21 1 1
()
dA
AA A
dx
∞
=γ − .
Разделяя переменные и интегрируя, имеем
0
0
/
2
22
22
11 20
/
22
122
() (0)
(0)( 1)
xx
xx
Ae
Ax A A
AA e
∞
∞
γ
=+
γ+ −
,
где
21 2 2 2 2 2 2
22
012 22 1 22 1
11
( ) , (0) (0), (0) (0).xAAA AAA A
−
∞∞∞ ∞
γγ
=− γ = − = −
γγ
С учетом
1
()Ax из (5.12) получаем
0
0
/
2
2
22
/
22
22
() (0)
(0)( 1)
xx
xx
Ae
Ax A
AA e
∞
∞
=
+
−
.
В соответствии с полученными решениями амплитуда волны накачки
1
()Ax убывает от
1
(0)A до A
1∞
, а амплитуда второй гармоники растет от
2
(0)A до
2
A
∞
.
Пример 3
Исследовать взрывную неустойчивость, описываемую уравнением
()
()
0
2
;, 0, 0 ,
dA
A
AAA
dt
=γ −ν γν= =
где А
(0)
– пороговое значение.
Решение
Пороговое значение находится из соотношения
(
)
(
)
02 0
0AAγ−ν=
и равняется
()
0
.A
ν
=
γ
Тогда исходное соотношение примет вид
()
()
dA
dt
AA A=−
γ
0
.
Проинтегрируем это уравнение методом разделения переменных:
(0)
(0)
exp( )
A
CAt
AA
=
−γ
−
.
Из начального условия следует, что
(0)
(0)
.
(0)
A
C
AA
=
−
Тогда
(0)
(0)
(0)
() .
1 1 exp( )
(0)
A
At
A
At
A
=
⎛⎞
−
−γ
⎜⎟
⎝⎠
Глава 5. Когерентное взаимодействие волн. Неустойчивости.
5.2. Примеры
59
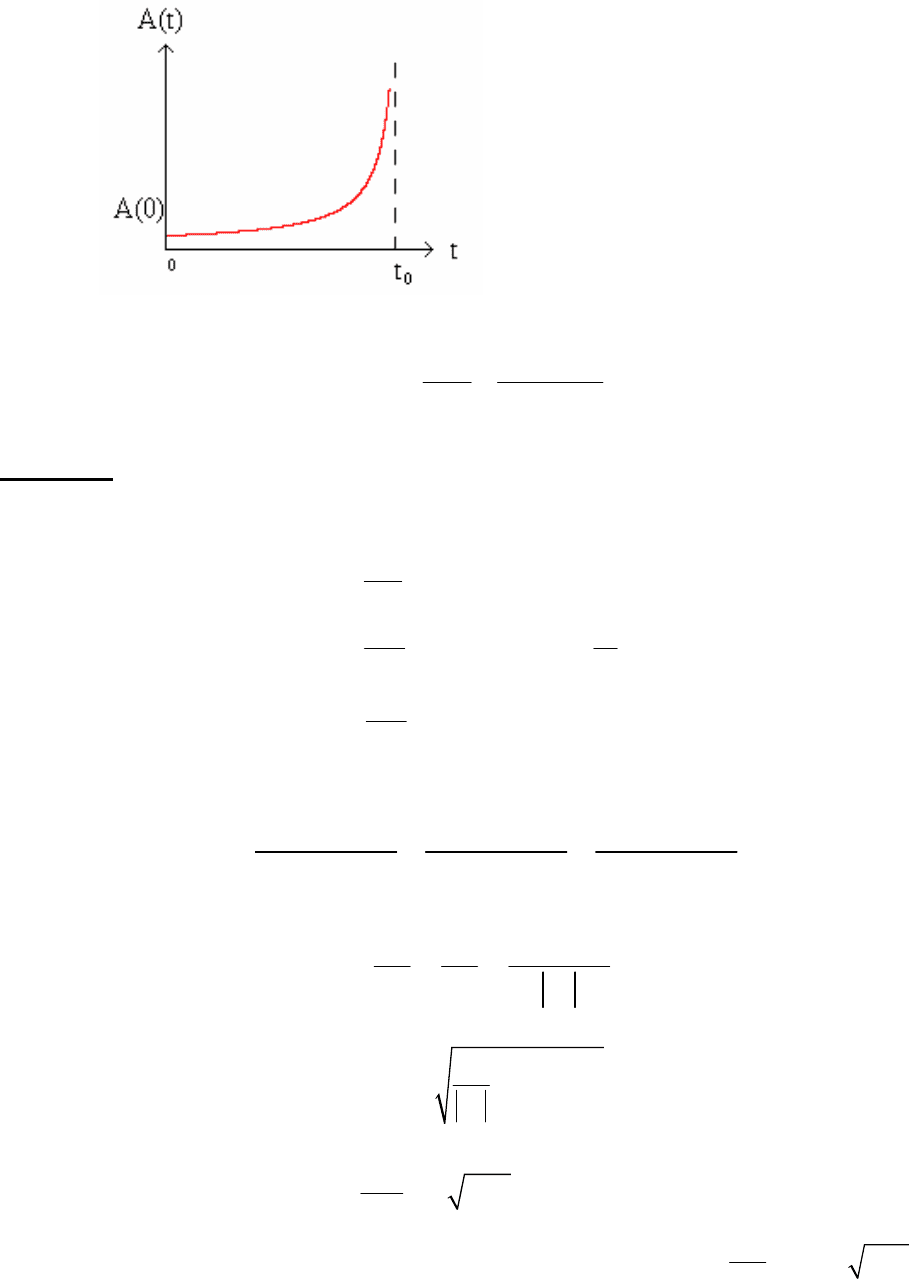
Видно, что при
(0)
(0)AA≤ взрывная неустойчивость не возникает, она имеет место при
(0)
(0)AA> .
Рис. 5.2. Вид решения А(t).
Время развития взрывной неустойчивости равно
0
(0) (0)
1(0)
ln .
(0)
A
t
AAA
=
γ−
Пример 4
В результате трехволнового взаимодействия могут возникать солитоны огибающих. Они
описываются следующей моделью:
1
102 1 2 0
;, 0; 0;
dA
AA
dt
=γ γ γ > γ <
(5.16)
2
201
;;
г
dA
x
AA t t
dt v
′
=γ = −
(5.17)
0
012 1,2 0
;()0;() .
dA
A
AA A A
dt
∞
=γ ±∞ = ±∞ =
(5.18)
Решение
Из соотношения Мэнли – Роу имеем:
22
22 22
00
11 22
120
()
() ()
AA
AA AA
−
±∞
−±∞ −±∞
==
γγγ
или
22
22
00 0
12
12 0
.
A
A
AA
−
==
γγ γ
Отсюда
1,2
22
1,2 00 0
0
().
A
AA
γ
=−
γ
(5.19)
Подставим (5.19) в (5.18) и получим
()
22
0
12 00 0
dA
A
A
dt
=− γγ −
.
Для удобства интегрирования данного уравнения введем
0
00
A
y
A
=
и
12 00
0Aλ= γγ >
.
Тогда
