Ларин Р.М., Пяткин А.В., Плясунов А.В. Методы оптимизации примеры и задачи
Подождите немного. Документ загружается.


m
P
i=1
n
P
j=1
c
ij
x
ij
−→
min
,
n
P
j=1
α
ij
x
ij
= a
i
, i = 1, m,
m
P
i=1
β
ij
x
ij
= b
j
, j = 1, n,
x
ij
≥ 0, i = 1, m, j = 1, n.
x y
w(x) ≥ z(y).
x y
w(x) = z(y) x y
x
1
− x
2
→ min, y
1
+ 2y
2
→ max,
x
1
+ x
2
= 1, y
1
+ y
2
= 1,
x
1
+ x
2
= 2; y
1
+ y
2
= −1.
x y
y
i
(a
i
x − b
i
) = 0 (i ∈ I),
(c
j
− yA
j
)x
j
= 0 (j ∈ J).
a
−5y
1
+ 8y
2
≤ a,
y
1
− y
2
≤ −3,
y
1
− 2y
2
≤ 3,
2y
1
− 3y
2
≤ 1
0 −→ max,
ax
1
− 3x
2
+ 3x
3
+ x
4
→ min
−5x
1
+ x
2
+ x
3
+ 2x
4
= 0,
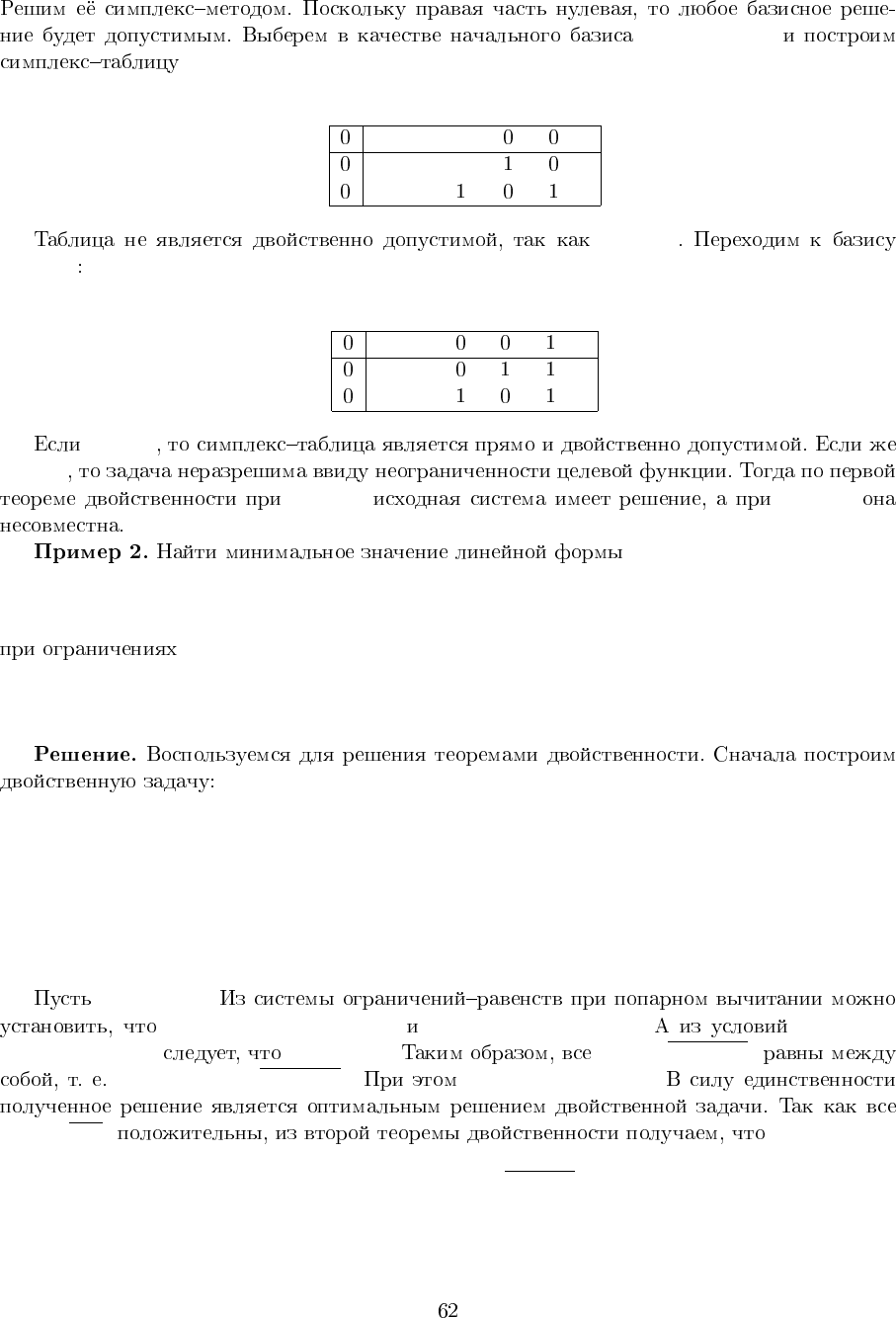
8x
1
− x
2
− 2x
3
− 3x
4
= 0,
x
i
≥ 0, i = 1, 2, 3, 4.
B = (A
3
, A
4
)
x
1
x
2
x
3
x
4
−w a + 5 −1
x
3
−1 −1
x
4
−2
z
02
< 0
(A
3
, A
2
)
x
1
x
2
x
3
x
4
−w a + 3
x
3
−3
x
2
−2
a ≥ −3
a < −3
a ≥ −3 a < −3
w(x) = x
1
+ x
2
+ ··· + x
n
x
j
+ x
j+1
≥ α
j
, j = 1, . . . , n − 1,
x
1
+ x
n
≥ α
n
.
z(y) =
n
X
i=1
α
i
y
i
→ max
y
i
+ y
i+1
= 1, i = 1, . . . , n − 1,
y
1
+ y
n
= 1,
y
i
≥ 0, i = 1, . . . , n.
n = 2k + 1.
y
1
= y
3
= ··· = y
2k+1
y
2
= y
4
= ··· = y
2k
. y
1
+ y
2
=
1, y
1
+ y
2k+1
= 1 y
2
= y
2k+1
. y
i
(i = 1, 2k + 1)
y
i
= 1/2 (i = 1, 2k + 1). z(y) = 1/2
P
n
i=1
α
i
.
y
i
(i = 1, n)
x
j
+ x
j+1
= α
j
, j = 1, n − 1,
x
1
+ x
n
= α
n
.

w(x) = 1/2
P
n
i=1
α
i
= z(y).
j = 1, 2x
1
=
P
k
s=0
α
2s+1
−
P
k
s=1
α
2s
,
x
1
=
1
2
n
X
s=1
(−1)
s+1
α
s
.
x :
x
j
= (−1)
j−1
³
j−1
X
s=1
(−1)
s
α
s
+ x
1
´
, j = 2, . . . , 2k + 1.
n = 2k. y
1
= y
3
= ··· = y
2k−1
y
2
= y
4
=
··· = y
2k
.
z(y) =
³
k
X
s=1
α
2s−1
´
y
1
+
³
k
X
s=1
α
2s
´
y
2
,
y
1
+ y
2
= 1, y
1
≥ 0, y
2
≥ 0. z(y)
P
k
s=1
α
2s−1
>
P
k
s=1
α
2s
, y
1
= 1, y
2
= 0.
P
k
s=1
α
2s−1
<
P
k
s=1
α
2s
, y
1
= 0, y
2
= 1.
P
k
s=1
α
2s−1
=
P
k
s=1
α
2s
z(y) = max
n
k
X
s=1
α
2s−1
,
k
X
s=1
α
2s
o
.
P
k
s=1
α
2s−1
≥
P
k
s=1
α
2s
. y
2s−1
= 1, y
2s
= 0 (s = 1, k).
x
2s−1
+ x
2s
= α
2s−1
, (s = 1, k). (∗)
w(x) =
P
n
j=1
x
j
=
P
k
s=1
α
2s−1
= z(y).
(∗)
x
2s
+ x
2s+1
≥ α
2s
, (s = 1, . . . , k − 1),
x
2k
+ x
1
≥ α
2k
,
n = 2k
x
1
+ 2x
2
+ 3x
3
+ 4x
4
−→ min,
x
1
+ x
2
+ x
3
+ x
4
≥ 1,
x
1
≥ 0, x
2
≥ 0, x
3
≥ 0, x
4
≥ 0
x
1
+ x
2
+ x
3
+ x
4
−→ min
x
1
− x
2
≥ 0, x
1
+ x
2
− x
3
+ x
4
− x
5
≥ 1,
x
1
≥ 0, x
2
≥ 0, x
3
≥ 0, x
4
≥ 0, x
5
≥ 0

x
1
+ 5x
2
+ x
3
+ 10x
4
+ x
5
+ 3x
6
−→ min
−x
1
+ x
2
+ x
3
+ x
4
≥ 1, x
1
+ 2x
2
− x
3
+ 3x
4
− x
5
− x
6
≥ 1
x
1
≥ 0, x
2
≥ 0 x
3
≥ 0, x
4
≥ 0, x
5
≥ 0, x
6
≥ 0
3x
1
+ 5x
2
+ 4x
3
−→ min
x
1
+ 2x
2
+ 3x
3
≥ 1, 2x
1
+ 3x
2
+ x
3
≥ 1, 3x
1
+ x
2
+ 2x
3
≥ 1,
6x
1
+ 6x
2
+ 6x
3
≥ 1, 2x
1
+ 4x
3
≥ 1
x
1
− x
2
+ x
3
−→ min,
x
1
− x
2
+ 2x
3
≥ 0, x
1
+ x
2
− x
3
≥ 0, −x
1
+ 2x
2
+ x
3
≥ 1,
x
1
+ x
3
≥ 2, −2x
1
− 2x
2
− 3x
3
≥ 3
x
1
+ 2x
2
+ 3x
3
+ ··· + nx
n
−→ min,
x
1
+ x
2
+ ··· + x
i
≥ i, i = 1, n,
x
j
≥ 0, j = 1, n;
x
1
+ x
2
+ x
3
−→ min,
λx
1
+ x
2
+ x
3
≥ µ
1
, x
1
+ λx
2
+ x
3
≥ µ
2
, x
1
+ x
2
+ λx
3
≥ µ
3
;
x
1
+ λx
2
+ λ
2
x
3
−→ min,
(1 + λ)x
1
+ x
2
+ x
3
≥ µ
1
, x
1
+ (1 + λ)x
2
+ x
3
≥ µ
2
, x
1
+ x
2
+ (1 + λ)x
3
≥ µ
3
n
P
j=1
a
ij
x
j
= b
i
, i = 1, m
m
P
i=1
a
ij
y
i
≤ 0, j = 1, n,
m
P
i=1
b
i
y
i
> 0;
m
P
i=1
a
ij
y
i
≤ c
j
, j = 1, n
n
P
j=1
a
ij
x
j
= 0, i = 1, m
n
P
j=1
c
j
x
j
≥ 0;
m
P
i=1
b
i
y
i
= b
m
P
i=1
a
ij
y
i
= c
j
, j = 1, n
n
P
j=1
a
ij
x
j
= b
i
, i = 1, m,
n
P
j=1
c
j
x
j
= b
a

1) − 5y
1
− 2y
2
≤ a 2) 9y
1
+ 16y
2
≥ a 3) − 3y
1
− y
2
≤ a + 5
−4y
1
+ y
2
≤ 5, 7y
1
− 8y
2
≤ 9, y
1
− 3y
2
− 4y
3
≤ 1,
2y
1
+ y
2
≤ 2, y
1
+ y
2
≤ 1, y
1
+ y
3
≤ 1,
3y
1
+ y
2
≤ 4; y
1
+ 2y
2
≤ −1; −2y
1
+ y
2
+ y
3
≤ 1,
y
2
+ y
3
≤ −2?
x
∗
B
= B
−1
b, x
∗
N
= 0, y
∗
= c
B
B
−1
, x
∗
y
∗
B
z
0j
≥ 0, j ∈ J
z
i0
≥ 0, i ∈ I
r : z
r0
< 0, r ≥ 1
{j | z
rj
< 0, j ≥ 1} 6= ∅ s
z
0s
|z
rs
|
= min{
z
0j
|z
rj
|
| z
rj
< 0, j ≥ 1},
X = ∅
σ(r) := s
z
0j
j |{j | z
0j
>
0, j ≥ 1}| = n − m
cx → min
Ax ≤ b,
x ≥ 0,
c
w(x) = x
1
+ 3x
2
→ min,
x
1
+ x
2
+ x
3
≤ 4,
x
1
− x
2
+ x
3
≤ −1,
x
i
≥ 0, i = 1, 2, 3.

c = (1, 3, 0)
w(x) = x
1
+ 3x
2
→ min,
x
1
+ x
2
+ x
3
+ x
4
= 4,
x
1
− x
2
+ x
3
+ x
5
= −1,
x
i
≥ 0, i = 1, 2, 3, 4, 5.
B = (A
4
, A
5
)
x
1
x
2
x
3
x
4
x
5
−w 0 1 3 0 0 0
x
4
4 1 1 1 1 0
x
5
−1 1 −1 1 0 1
z
20
=
−1 < 0 r = 2, s = 2
x
1
x
2
x
3
x
4
x
5
−w −3 4 0 3 0 3
x
4
3 2 0 2 1 1
x
2
1 −1 1 −1 0 −1
B = (A
2
, A
4
)
x
∗
= (0, 1, 0, 3, 0)
>
w(x
∗
) = 3.
B
0
−x
1
− 2x
2
+ 4x
3
−→ min
x
1
+ x
2
− 3x
3
= 0, x
1
− 2x
2
+ x
3
= 3
x
1
≥ 0, x
2
≥ 0, x
3
≥ 0
B
0
= (A
1
, A
2
)
−x
1
+ 7x
2
+ 5x
3
+ 35x
4
−→ min
2x
1
+ 6x
2
− 8x
3
− 30x
4
= 6, x
1
− x
2
+ x
3
+ x
4
= −5
x
1
≥ 0, x
2
≥ 0, x
3
≥ 0, x
4
≥ 0
B
0
= (A
1
, A
2
)
−x
1
− x
2
− x
3
+ x
5
−→ min
x
1
+ x
2
− 4x
4
+ 2x
5
= −2, x
2
+ x
3
+ x
4
− 2x
5
= −2, x
1
+ x
3
+ 3x
4
− 2x
5
= −2
x
1
≥ 0, x
2
≥ 0, x
3
≥ 0, x
4
≥ 0, x
5
≥ 0
B
0
= (A
1
, A
2
, A
3
)

x
n+1
x
n+1
→ min
x∈
e
X
,
e
X = {x = (x
1
, ..., x
n
, x
n+1
) ∈ E
n+1
| ϕ
j
(x
1
, ..., x
n
) ≤ 0 (j = 1, m), f(x
1
, ..., x
n
) − x
n+1
≤ 0}.
f(x
1
, ..., x
n
)
f(x) =< c, x >→ min
x∈X
, (1)
X = {x = (x
1
, ..., x
n
) ∈ E
n
| ϕ
j
(x) ≤ 0 (j = 1, m)}, (2)
c ϕ
j
(x) (j = 1, m)}
x ∈ X I(x) = {j ∈ {1, ..., m}| ϕ
j
(x) = 0 }
J(x, δ) = {j ∈ {1, ..., m}| − δ < ϕ
j
(x) ≤ 0 },
δ
δ
0
> 0 x
0
∈ X k
δ
k
> 0 x
k
∈ X (k ≥ 0)
σ → min
σ,p
, (3)
< c, p >≤ σ, (4)
< ϕ
0
j
(x
k
), p >≤ σ (j ∈ J(x
k
, δ
k
)), (5)
|p
i
| ≤ 1 (i = 1, n), (6)
p
(σ
k
, p
k
)
σ
k
≤ 0
σ → min
σ,p
,
< c, p >≤ σ,
< ϕ
0
j
(x
k
), p >≤ σ (j ∈ I(x
k
)), (7)
|p
i
| ≤ 1 (i = 1, n).

I(x
k
) ⊆ J(x
k
, δ
k
) σ
k
≤ σ
k
σ
k
B
(σ
∗
, p
∗
)
B x
∗
∈ X σ
∗
= 0 x
∗
k δ
k
> 0
x
k
∈ X (k = 0, 1, ...)
A (σ
k
, p
k
)
σ
k
< −δ
k
δ
k+1
= δ
k
−δ
k
≤ σ
k
< 0 δ
k+1
= δ
k
/2
σ
k
= 0 B σ
k
, p
k
σ
k
= 0 x
k
σ
k
< 0 δ
k+1
= δ
k
/2, p
k
= p
k
α
k
p
k
α
kj
ϕ
j
(x
k
+ αp
k
) = 0.
α
k
= min{α
kj
| 1 ≤ j ≤ m }.
x
k+1
= x
k
+ α
k
p
k
,
J(x
k+1
, δ
k+1
) = {j| − δ
k+1
< ϕ
j
(x
k+1
) ≤ 0 },
I(x
k+1
) = {j| ϕ
j
(x
k+1
) = 0 }.
k := k + 1
ϕ
j
(x) (j = 1, m)
X
{f(x
k
)} f
∗
= min
x∈X
f(x)
f(x
k
) =< c, x
k
>→ f
∗
k → ∞
x
∗
{x
k
}
f(x) X
x
0
∈ X
ξ → min
ϕ
j
(x) ≤ ξ (j = 1, m).
(ξ
0
, x
0
) x
0
∈ E
n
, ξ
0
≥ max
1≤j≤m
ϕ
j
(x
0
)
ξ
k
≤ 0
x
0
:= x
k

| min
x∈X
< c, x > − < c, x
k
> | ≤ | min
x∈X
k
< c, x > − < c, x
k
> |,
k
< c, x >→ min
x∈X
k
,
X
k
= {x| ϕ
j
(x
k
)+ < ϕ
0
j
(x
k
), x − x
k
>≤ 0 (j = 1, m) }.
p A B
|p
i
| ≤ 1 (i = 1, n)
z(x) = x
3
→ min
x
1
,x
2
,x
3
ϕ
1
(x) ≡ x
2
1
+ 2x
1
x
2
+ 2x
2
2
− 2x
1
− x
2
− x
3
− 2 ≤ 0,
ϕ
2
(x) ≡ x
2
1
+ x
2
2
− x
1
+ x
2
− x
3
− 3 ≤ 0,
ϕ
3
(x) ≡ x
2
1
+ x
1
− 4x
2
− x
3
+ 3 ≤ 0,
x
0
= (1, −1, 9)
>
δ
0
= 0.5 J(x
0
, δ
0
) = I(x
0
) = {3} ϕ
1
(x
0
) = −11 <
−δ
0
, ϕ
2
(x
0
) = −12 < −δ
0
, ϕ
3
(x
0
) = 0 > −δ
0
A
σ → min,
< c, p > −σ ≡ p
3
− σ ≤ 0,
< ϕ
0
3
(x
0
), p > −σ ≡ 3p
1
− 4p
2
− p
3
− σ ≤ 0,
−p
1
− 1 ≤ 0, p
1
− 1 ≤ 0, −p
2
− 1 ≤ 0, p
2
− 1 ≤ 0.
A B < c, p >≤ σ
p
3
≤ σ σ
k
≤ 0 x
k

p
k
3
≤ 0 p
3
≥ −σ + 3p
1
− 4p
2
p
3
A B
|p
3
| ≤ 1
A p
0
= (−1, 1, −3.5)
>
, σ
0
= −3.5 σ
0
< −δ
0
δ
1
= δ
0
= 0.5
α
0
x
1
= 1 − α, x
2
= −1 + α, x
3
= 9 − 3.5α (α > 0).
ϕ
j
(x
0
+ αp
0
) = 0 (j = 1, 2, 3)
α
0
= 2.1 ϕ
2
(x
0
+ α
0
p
0
) ≈ 0
x
1
x
1
= x
0
+ α
0
p
0
= (−1.1, 1.1, 1.65)
>
,
ϕ
1
(x
1
) = −1.34 < −δ
1
, −δ
1
< ϕ
2
(x
1
) = −0.03, ϕ
3
(x
1
) = −2.94 < −δ
1
J(x
1
, δ
1
) = {2}
max
1≤j≤3
ϕ
j
(x
1
) = −0.03 6= 0 −δ
1
δ
α
δ
k
α
kj
> 0 −δ
k
< ϕ
j
(x
k
+ α
kj
p
k
) ≤ 0
j
A
σ → min,
< c, p > −σ ≡ p
3
− σ ≤ 0,
< ϕ
0
2
(x
1
), p > −σ ≡ −3.2p
1
+ 3.2p
2
− p
3
− σ ≤ 0,
−p
1
− 1 ≤ 0, p
1
− 1 ≤ 0, −p
2
− 1 ≤ 0, p
2
− 1 ≤ 0.
p
1
= (1, −1, −3.2)
>
, σ
1
= −3.2
σ
1
< −δ
1
δ
2
= δ
1
= 0.5
α
1
x
1
= −1.1 + α, x
2
= −1.1 − α, x
3
= 1.65 − 3.2α (α > 0).
ϕ
j
(x
1
+ αp
1
) = 0 (j = 1, 2, 3)
α
1
= 0.45 ϕ
3
(x
1
+ α
1
p
1
) ≈ 0
x
2
x
2
= x
1
+ α
1
p
1
= (−0.65, 0.65, 0.21)
>
.
ϕ
1
(x
2
) = −1.14 < −δ
2
, ϕ
2
(x
2
) = −1.07 < −δ
2
, −δ
2
< ϕ
3
(x
2
) = −0.04 < 0
J(x
2
, δ
2
) = {3}
