Ларин Р.М., Пяткин А.В., Плясунов А.В. Методы оптимизации примеры и задачи
Подождите немного. Документ загружается.


µ
−(1 + e
x
2
) cos x
1
−e
x
2
sin x
1
−e
x
2
sin x
1
e
x
2
(cos x
1
− x
2
− 2)
¶
.
(2kπ, 0) a
11
= −2, a
22
= −1 a
12
= a
21
= 0
((2k + 1)π, −2) a
11
= 1 + e
−2
> 0, a
22
= −e
−2
< 0
a
12
= a
21
= 0
x
0
p
k
∈ E
n
α
k
> 0 x
k+1
=
x
k
+ α
k
p
k
(k = 0, 1, . . .) p
k
α
k
f(x
k+1
) ≤ f(x
k
)
f(x) x
∗
x
∗
?”
n > 1
f(x) = (x
1
−x
2
2
)(2x
1
−x
2
2
) x
∗
= (0, 0)
>
x
1
= ax
2
x
∗
x
2
= 0
f(x
1
, 0) = 2x
2
1
x
1
= 0 x
1
= ax
2
f(x)
e
f(x
2
) = f(ax
2
, x
2
) = (ax
2
− x
2
2
)(2ax
2
− x
2
2
) a = 0
e
f(x
2
) = x
4
2
x
2
= 0
e
f
0
(x
2
) = (a − 2x
2
)(2ax
2
− x
2
2
) + (ax
2
− x
2
2
)(2a − 2x
2
),
e
f
00
(x
2
) = −2(2ax
2
− x
2
2
) + 2(a − 2x
2
)(2a − 2x
2
) − 2(ax
2
− x
2
2
).
a 6= 0
e
f
0
(0) = 0
e
f
00
(0) = 4a
2
> 0
x
∗
f(x)
f(x) x
∗
X
1
= {x | x
1
> x
2
2
}, X
2
= {x | 2x
1
< x
2
2
}
X
3
= {x | x
2
2
> x
1
> x
2
2
/2}
f(0, 0) = 0 x
∗
f(x)
f(x) = x
2
1
+ 2x
2
2
+ 5x
2
3
− 2x
1
x
2
− 4x
1
x
3
− 2x
3
f(x) = x
4
1
+ x
2
2
− 4x
1
x
2
f(x) = x
1
e
x
1
− (1 + e
x
1
) sin x
2
f(x)

f(x) = −(x
2
2
+ 1)(sin x
1
+ 2)
f(x) = sin x
1
− x
2
2
E
n
f(x) −→ min
x∈X
(f(x) −→ max
x∈X
), (1)
X = {x ∈ E
n
| ϕ
j
(x) = 0, j = 1, m}. (2)
m ≤ n
m n m ≤ n
F
j
(x
1
, . . . , x
n
) = 0 (j = 1, m); (3)
F
j
(x)
U
ε
(x
0
) x
0
F
j
(x
0
) = 0
j = 1, m, ε > 0
¯
¯
¯
¯
¯
¯
¯
∂F
1
(x
0
)
∂x
1
. . .
∂F
1
(x
0
)
∂x
m
. . . . . . . . .
∂F
m
(x
0
)
∂x
1
. . .
∂F
m
(x
0
)
∂x
m
¯
¯
¯
¯
¯
¯
¯
6= 0.
x
0
U
ε
(x
0
)
x
1
, . . . , x
m
x
m+1
, . . . , x
n
x
i
= f
i
(x
m+1
, . . . , x
n
) (i = 1, m);
x
i
= x
0
i
(i = m + 1, n) x
0
i
(i = 1, m)
f
i
(x
0
m+1
, . . . , x
0
n
) = x
0
i
(i = 1, m);
f
i
(x
m+1
, . . . , x
n
) (i = 1, m)
f(x) X
f(x), ϕ
j
(x) (j = 1, m)
U
ε
(x
∗
)
x
∗
∂ϕ
1
(x
∗
)
∂x
1
. . .
∂ϕ
1
(x
∗
)
∂x
n
. . . . . . . . .
∂ϕ
m
(x
∗
)
∂x
1
. . .
∂ϕ
m
(x
∗
)
∂x
n
(4)

m
¯
¯
¯
¯
¯
¯
¯
∂ϕ
1
(x
∗
)
∂x
1
. . .
∂ϕ
1
(x
∗
)
∂x
m
. . . . . . . . .
∂ϕ
m
(x
∗
)
∂x
1
. . .
∂ϕ
m
(x
∗
)
∂x
m
¯
¯
¯
¯
¯
¯
¯
6= 0.
x
∗
ϕ
j
(x) = 0 (j = 1, m) (3
0
)
x
i
= f
i
(x
m+1
, . . . , x
n
) (i = 1, m), (5)
f
i
0
F (x
m+1
, . . . , x
n
) ≡ f(f
1
(x
m+1
, . . . , x
n
), . . . , f
m
(x
m+1
, . . . , x
n
), x
m+1
, . . . , x
n
)) (6)
x
∗
0
x
i
(i = 1, m)
y
j
(j = 1, m)
F (x, y) = f(x) +
m
X
j=1
y
j
ϕ
j
(x).
y
j
F (x, y)
x
∗ 0
x
∗
y
∗
j
(j = 1, m),
∂F (x
∗
, y
∗
)
∂x
i
= 0 (i = 1, n), (7)
∂F (x
∗
, y
∗
)
∂y
j
= 0 (j = 1, m). (8)
0
X
f(x) = x
1
+ x
2
+ x
3
+ x
4
ϕ(x) = x
1
x
2
x
3
x
4
− a
4
= 0 (a > 0) X = {x
i
> 0 | i = 1, n}

X y F (x, y) = f(x) + yϕ(x)
F
0
x
1
(x, y) = 1 + x
2
x
3
x
4
y = 0,
F
0
x
2
(x, y) = 1 + x
1
x
3
x
4
y = 0,
F
0
x
3
(x, y) = 1 + x
1
x
2
x
4
y = 0,
F
0
x
4
(x, y) = 1 + x
1
x
2
x
3
y = 0,
F
0
y
(x, y) = x
1
x
2
x
3
x
4
− a
4
= 0.
y 6= 0 −1/y = x
1
x
2
x
3
= x
1
x
2
x
4
=
x
1
x
3
x
4
= x
2
x
3
x
4
. x
1
= x
2
= x
3
= x
4
x
i
= a i = 1, 2, 3, 4.
f(x) =
n
X
i=1
n
X
j=1
a
ij
x
i
x
j
,
a
ij
= a
ji
, X = {x |
P
n
i=1
x
2
i
= 1}
X
(2x
1
, 2x
2
, . . . , 2x
n
)
X
F (x, y) = f(x) + y(1 −
n
X
i=1
x
2
i
).
n
X
j=1
a
ij
x
j
− yx
i
= 0 (i = 1, n). (9)
n n
¯
¯
¯
¯
¯
¯
¯
¯
a
11
− y a
12
. . . a
1n
a
21
a
22
− y . . . a
2n
. . . . . . . . . . . .
a
n1
a
n2
. . . a
nn
− y
¯
¯
¯
¯
¯
¯
¯
¯
= 0. (10)
y A
x ∈ X
i x
i
f(x) − y
n
X
i=1
x
2
i
= 0,
x ∈ X, f(x) = y
f(x) X
A

x
2
1
/a
2
1
+ x
2
2
/a
2
2
+ x
2
3
/a
2
3
= 1, a
1
> a
2
> a
3
> 0
b
1
x
1
+ b
2
x
2
+ b
3
x
3
= 0 b
i
6= 0
f(x) = x
2
1
+ x
2
2
+
x
2
3
X = {x | x
2
1
/a
2
1
+ x
2
2
/a
2
2
+ x
2
3
/a
2
3
= 1 b
1
x
1
+ b
2
x
2
+ b
3
x
3
= 0}
µ
2x
1
/a
2
1
2x
2
/a
2
2
2x
3
/a
2
3
b
1
b
2
b
3
¶
= 1,
x
i
= ca
2
i
b
i
i = 1, 2, 3 c ∈ E
1
x
2
1
a
2
1
+
x
2
2
a
2
2
+
x
2
3
a
2
3
= c
2
b
2
1
a
2
1
+ c
2
b
2
2
a
2
2
+ c
2
b
2
3
a
2
3
= c(b
1
x
1
+ b
2
x
2
+ b
3
x
3
) = 0,
x /∈ X
F (x, y) = x
2
1
+ x
2
2
+ x
2
3
+ y
1
(
x
2
1
a
2
1
+
x
2
2
a
2
2
+
x
2
3
a
2
3
− 1) + y
2
(b
1
x
1
+ b
2
x
2
+ b
3
x
3
).
x
x
i
+
y
1
x
i
a
2
i
+
y
2
b
i
2
= 0 (i = 1, 2, 3). (11)
x
i
y
1
= −f(x)
(1+y
1
/a
2
i
) 6= 0 i (1+y
1
/a
2
1
) = 0
y
2
= 0 x
2
(1 + y
1
/a
2
2
) = 0 x
3
(1 + y
1
/a
2
3
) = 0 b
1
x
1
+
b
2
x
2
+ b
3
x
3
= 0 x
2
, x
3
(1 + y
1
/a
2
2
) = 0 (1 + y
1
/a
2
3
) = 0 a
1
> a
2
> a
3
x
i
= −
y
2
b
i
a
2
i
2(a
2
i
+ y
1
)
(i = 1, 2, 3).
3
X
i=1
b
i
x
i
= −y
2
3
X
i=1
b
2
i
a
2
i
2(a
2
i
+ y
1
)
= 0.
y
2
6= 0 x
i
3
X
i=1
b
2
i
a
2
i
a
2
i
+ y
1
= 0.
f(x) = −y
1
y = x
2
x − y − 2 = 0
(x
1
, y
1
) (x
2
, y
2
)
f(x
1
, y
1
, x
2
, y
2
) = (x
1
−x
2
)
2
+ (y
1
−y
2
)
2
y
1
− x
2
1
= 0 x
2
− y
2
− 2 = 0

µ
−2x
1
1 0 0
0 0 1 −1
¶
,
F (x, y, z) = (x
1
− x
2
)
2
+
(y
1
− y
2
)
2
+ z
1
(y
1
− x
2
1
) + z
2
(x
2
− y
2
− 2)
F
0
x
1
= 2(x
1
− x
2
) − 2x
1
z
1
= 0,
F
0
x
2
= −2(x
1
− x
2
) + z
2
= 0,
F
0
y
1
= 2(y
1
− y
2
) + z
1
= 0,
F
0
y
2
= −2(y
1
− y
2
) − z
2
= 0.
(12)
z
2
= 2x
1
z
1
z
1
= z
2
z
1
= z
2
= 0, y
1
= y
2
x
1
=
x
2
y = x
2
, x − y − 2 = 0 z
1
6= 0 x
1
= 1/2.
y
1
= 1/4
x
2
+ y
2
= x
1
+ y
1
= 3/4 x
2
= y
2
+ 2,
x
2
= 11/8, y
2
= −5/8
p
f(1/2, 1/4, 11/8, −5/8) = 7
√
2/8.
f(x) = x
1
x
3
1
−x
2
2
= 0
x
1
= (x
2
)
2/3
≥ 0 x
∗
= (0, 0)
F (x, y) = x
1
+y(x
3
1
−x
2
2
)
F
0
x
1
= 1 + 3yx
2
1
= 0,
F
0
x
2
= −2yx
2
= 0,
F
0
y
= x
3
1
− x
2
2
= 0,
(13)
(3x
2
1
, −2x
2
) x
∗
= (0, 0)
(0, 0)
f(x) = x
1
x
2
x
3
−→ extr
X
X = {x | x
2
1
+ x
2
2
+ x
2
3
= 1, x
1
+ x
2
+ x
3
= 0}
f(x) = x
1
x
2
x
3
−→ extr
X
X = {x | x
1
+ x
2
+ x
3
= 5, x
1
x
2
+ x
2
x
3
+ x
1
x
3
= 8}
f(x) = x
1
x
2
2
x
3
3
−→ extr
X
X = {x | x
1
+ 2x
2
+ 3x
3
= a, x
1
> 0, x
2
> 0 x
3
> 0} (a > 0)
f(x) = x
1
+ x
2
+ x
3
−→ extr
X
X = {x | x
2
1
+ x
2
2
= 1, x
1
+ x
2
− x
3
= 0}
f(x) = x
2
−→ extr
X
X = {x | x
3
1
+ x
3
2
− 3x
1
x
2
= 0}
f(x) = x
1
+ x
2
+ x
2
3
+ 2(x
1
x
2
+ x
1
x
3
+ x
2
x
3
) −→ extr
X
X = {x | x
2
1
+ x
2
2
+ x
3
= 1}

x
2
+ y
2
+ z
2
= 1 N
(x
i
, y
i
, z
i
)
>
, i = 1, N
a n
(x
2
+ y
2
+ z
2
)
2
= a
2
(x
2
+ y
2
− z
2
) (a > 0)
(x
0
, y
0
, z
0
)
>
a
1
x
1
+ a
2
x
2
+ a
3
x
3
+
a
0
= 0
f(x) −→
x∈X
X = {x ∈ E
n
| ϕ
j
(x) ≤ 0 (j = 1, m)}
ϕ
j
(x) (j = 1, m)
E
n
f(x)
X X
ϕ
j
X
f(x)
X
f(x) X
f(x) X
X
C
0
m
+ C
1
m
+ . . . + C
min(m,n)
m
f(x) −→
x∈X
I
X
I
= {x | ϕ
j
(x) = 0 (j ∈ I)}
I ⊂ {1, 2, . . . , m} I = ∅
I n
f(x)
n
m
X
x
i
= ψ
i
(t) ( i = 1, n) x(t) ∈ X t ≥ 0 f(x(t)) → ±∞ t → +∞
f(x) = x
2
1
− x
1
x
2
+ x
2
2
X = {x | |x
1
| + |x
2
| ≤ 1}
X X
f
0
x
1
(x) = 2x
1
−x
2
f
0
x
2
(x) = −x
1
+2x
2
(0, 0)
>
X x
1
+ x
2
= 1, −x
1
+ x
2
=

1, x
1
− x
2
= 1 − x
1
− x
2
= 1 f(x)
x
1
+ x
2
= 1
e
f(x
1
) = f (x
1
, 1 − x
1
) = 3x
2
1
− 3x
1
+ 1
e
f
0
(x
1
) = 6x
1
−3 x
1
= 1/2 x
2
= 1/2
(1/2, 1/2)
>
f(x
1
, 1 + x
1
) = x
2
1
+ x
1
+ 1
(−1/2, 1/2)
>
f(x)
(−1/2, −1/2)
>
(1/2, −1/2)
>
X
(0, 1)
>
, (0, −1)
>
, (1, 0)
>
(−1, 0)
>
X
f(0, 0) = 0, f(1/2, 1/2) =
f(−1/2, −1/2) = 1/4, f(−1/2, 1/2) = f(1/2, −1/2) = 3/4, f(1, 0) = f(−1, 0) = f(0, 1) =
f(0, −1) = 1. f
X
f(x) = x
1
x
2
2
+ x
2
1
x
2
−
3x
2
1
− 3x
2
2
X = {x | − x
1
− x
2
+ 1 ≤ 0, x
1
+ x
2
− 16 ≤ 0}
X
1 ≤ x
1
+x
2
≤ 16 X
f(x)
½
f
0
x
1
= x
2
2
+ 2x
1
x
2
− 6x
1
= 0,
f
0
x
2
= 2x
1
x
2
+ x
2
1
− 6x
2
= 0.
(14)
(x
2
−x
1
)(x
1
+ x
2
+ 6) = 0 x
1
=
x
2
x
1
+ x
2
= −6
X x
1
= x
2
3x
2
1
−6x
1
= 0
x
1
= x
2
= 0 x
1
= x
2
= 2
X
F (x, y) = f(x) + y(x
1
+ x
2
− t) t = 1 t = 16
½
F
0
x
1
= x
2
2
+ 2x
1
x
2
− 6x
1
+ y = 0,
F
0
x
2
= 2x
1
x
2
+ x
2
1
− 6x
2
+ y = 0.
x
1
= x
2
t = 1
t = 16 (1/2, 1/2) (8, 8)
x
1
+ x
2
= 1 x
1
+ x
2
= 16 X
f(2, 2) =
−8, f(1/2, 1/2) = −5/4, f(8, 8) = 640.
X f(x)
x
1
= t, x
2
= s −t, t ∈ E
1
1 ≤ s ≤ 16
X f(t, s −t) = −(s + 6)t
2
+ (s
2
+
6s)t − 3s
2
−(s + 6) < 0 1 ≤ s ≤ 16 f(t, s − t) → −∞ t → ∞
X
f(x) = x
1
x
2
x
3
X = {x ∈ E
3
| x
1
+ x
2
+ x
3
≤ 6, x
1
x
2
+ x
2
x
3
+ x
1
x
3
≤ 8}
X
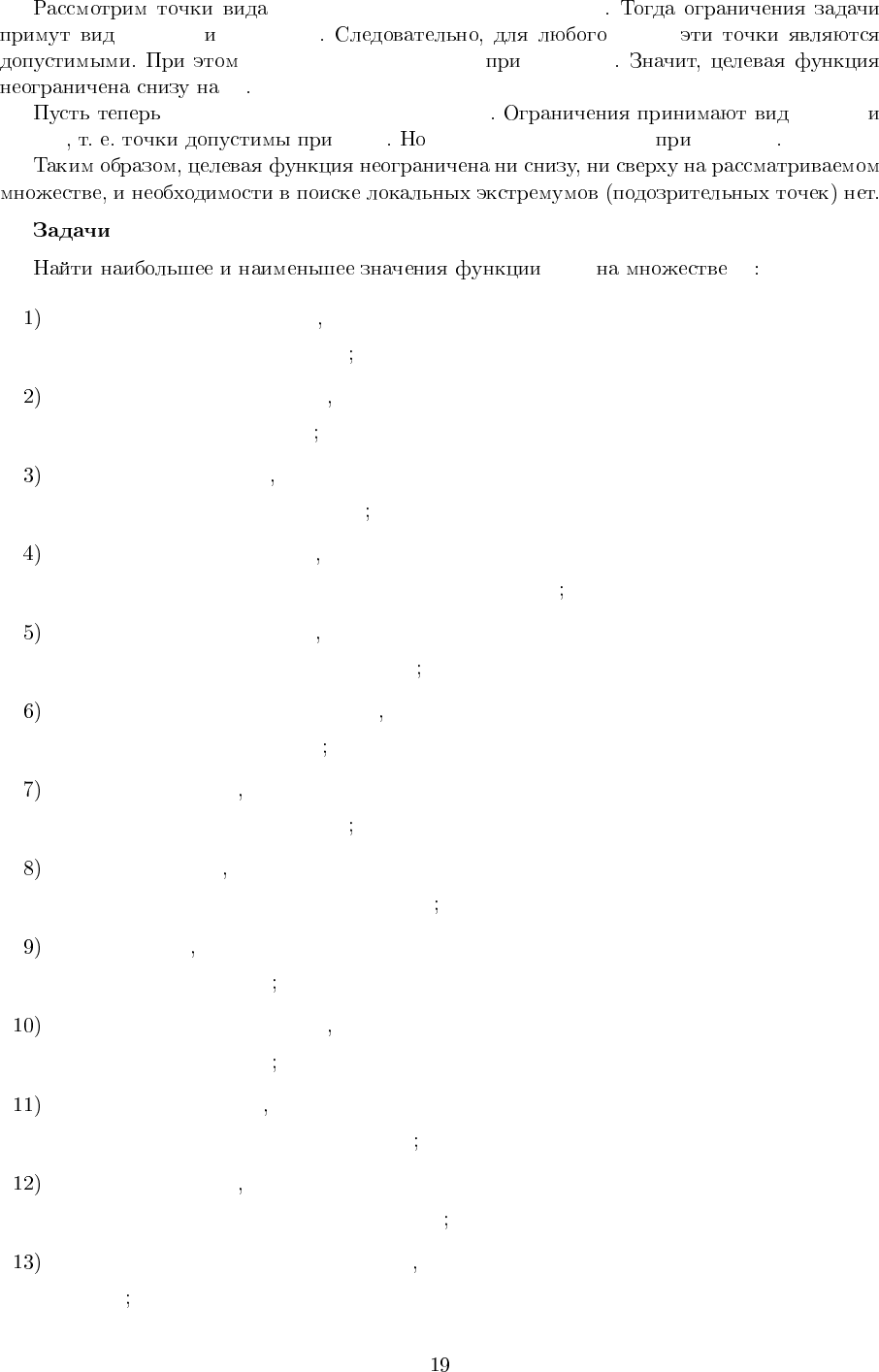
x
1
(t) = 1, x
2
(t) = 1, x
3
(t) = −t
−t ≤ 4 −t ≤ 7/2 t ≥ 0
f(1, 1, −t) = −t → −∞ t → +∞
X
x
1
(t) = 1, x
2
(t) = −1, x
3
(t) = −t −t ≤ 6
−1 ≤ 8 t ≥ 0 f(1, −1, −t) = t → +∞ t → +∞
f(x) X
f(x) = x
1
x
2
− x
2
1
− 2x
2
2
+ x
1
X = {x | x
1
∈ [0, 1], x
2
∈ [0, 1]}
f(x) = x
3
1
− 4x
2
1
+ 2x
1
x
2
− x
2
2
X = {x | |x
1
| ≤ 5, |x
2
| ≤ 1}
f(x) = x
3
1
+ x
3
2
− 3x
1
x
2
X = {x | x
1
∈ [0, 2], x
2
∈ [−1, 2]}
f(x) = (x
1
− 5)
2
+ (x
2
− 7)
2
X = {x | x
1
+ 2x
2
≤ 12, x
1
+ x
2
≤ 9, x
1
≥ 0, x
2
≥ 0}
f(x) = (x
1
− 3)
2
+ (x
2
− 5)
2
X = {x | x
2
1
+ x
2
2
≤ 10, 2x
1
+ 2x
2
= 5}
f(x) = x
1
(π − x
1
) sin x
2
+ x
2
cos x
1
X = {x | x
1
∈ [0, π], x
2
≥ 0}
f(x) = x
1
+ x
2
+ x
3
X = {x | x
2
1
+ x
2
2
≤ x
3
, x
3
≤ 1}
f(x) = 2x
1
x
2
+ x
3
X = {x | x
2
1
+ x
2
2
= 1, 0 ≤ x
3
≤ 2x
1
+ 1}
f(x) = x
2
1
− x
2
2
X = {x | x
2
1
+ x
2
2
≤ 16}
f(x) = x
2
1
+ x
2
2
− 12x
1
+ 16x
2
X = {x | x
2
1
+ x
2
2
≤ 25}
f(x) = arctg x
1
− ln x
2
X = {x | x
2
1
+ x
2
2
≤ 4, x
1
≥ 0, x
2
≥ 1}
f(x) = x
1
+ x
2
− x
3
X = {x | x
1
x
2
x
3
≤ 1, −x
1
+ x
2
− x
3
≤ 0}
f(x) = x
2
1
+ x
1
x
2
+ x
2
2
+ 3|x
1
+ x
2
+ 2|
X = E
2

f(x) = x
2
1
+ x
2
2
+ 2α|x
1
+ x
2
− 1|, α > 0
X = E
2
f(x) = x
2
1
+ x
2
2
+ 2 max{x
1
, x
2
}
X = E
2
X ⊂ E
n
x, y ∈ X α ∈ [0, 1]
z = αx + (1 − α)y ∈ X
x
1
, x
2
, . . . , x
m
z = α
1
x
1
+ α
2
x
2
+ . . . + α
m
x
m
α
i
≥ 0
α
1
+ α
2
+ . . . + α
m
= 1
X
f(x) X
x, y ∈ X α ∈ (0, 1) f(αx + (1 −α)y) ≤ αf (x) + (1−α)f (y)
x y
f(x)
−f(x)
f(x) X
f(x) X
x, y ∈ X hf
0
(x), y − xi ≤ f(y) − f(x)
f(x)
X B(x) =
³
∂
2
f(x)
∂x
i
∂x
j
´
i,j=1,n
x ∈ X
f(x)
X λ {x ∈ X | f(x) ≤ λ}
f(x)
X
f(
m
X
i=1
α
i
x
i
) ≤
m
X
i=1
α
i
f(x
i
),
x
i
∈ X , α
i
≥ 0 i = 1, m α
1
+ . . . + α
m
= 1
f(x)
X
f(x) X
x
∗
∈ X f(x)
X
f(x) X X
∗
f(x) X
f(x) X
x
∗
∈ X x ∈ X, x 6= x
∗
f(x) > f(x
∗
)
