Лапин Н.И. Теория и практика инноватики

Подождите немного. Документ загружается.

Раздел III. ИННОВАЦИОННЫЕ РИСКИ

120

Формула (6) как основа субъективного подхода в теории принятия

решений впервые была предложена в работах Г. Крамера и Д. Бернулли

еще в первой половине XVIII в. Аксиоматика и строгая математическая

разработка методологии рационального принятия решений с учетом

субъективной функции полезности были осуществлены много позже

Дж. Нейманом и О. Моргенштерном

После расчета ожидаемой полезности проекта часто бывает не-

обходимо вернуться к стоимостному представлению задачи оценки

риска, т. е. получить стоимостную оценку прибыльности проекта, эк-

вивалентную его ожидаемой полезности.

Стоимостная оценка прибыльности проекта Ï´ может быть получена

из уравнения

, (7)

где U

exp

= const (рассчитанная ожидаемая полезность); Ï ′— стоимостная оцен-

ка прибыльности проекта, эквивалентная ожидаемой полезности проекта.

Рассмотрим типовую задачу. Предположим, что руководство некой фир-

мы стоит перед выбором — внедрять или не внедрять новшество, которое с

вероятностью 0,6 принесет выручку 1 млн руб. и с вероятностью 0,4 принесет

нулевую выручку. Внедрение требует затрат в размере 0,5 млн руб.

Положим, что склонность к риску руководителей фирмы определяется

функцией полезности вида U(x) = ln(x + 1), где x — текущий объем средств

на счете фирмы, составляющий 1 млн руб. Пойдут ли руководители фирмы

на инновацию? Какую максимальную сумму руководство фирмы согласится

заплатить за услуги страхования вложенных инвестиций, полностью устра-

няющего возможные потери?

Решение

Вычислим ожидаемую полезность инновационного проекта без страхо-

вания инвестиций:

exp

= 0,6•ln [(1 – 0,5 + 1) +1] + 0,4•ln [(1–0,5 + 0) + 1] = 0,6•0,92 +

+ 0,4•0,40 = 0,71.

Выражение в курглых скобках под знаком логарифма представляет собой

прирост средств на счете фирмы, который равен начальному количеству средств

на счете минус инвестиции в проект плюс выручка от реализации проекта.

Вычислим стоимостную оценку прибыльности проекта, эквивалентную

его ожидаемой полезности:

0,71= ln (x

´+ 1) > x´= е

0,71

–1=1,03 млн руб.

Глава 6. Неопределенность и риск в инновацияХ 121

Таким образом, руководство фирмы будет инвестировать в проект, так как

даже с учетом своей несклонности к риску оно оценивает участие в проекте

(1,03 млн руб.) выше, чем неучастие (1 млн руб. — изначальная сумма средств на

счете фирмы). Или, рассуждая иначе, полезность внедрения новшества (0,71),

с точки зрения руководителей фирмы, выше полезности отказа от внедрения:

ln(1+1) = 0,69.

Вычислим ожидаемую полезность проекта в случае страхования инве-

стиций:

exp

= 0,6•ln[(1 – 0,5 + 1 + 0) + 1] + 0,4•ln [(1 – 0,5 + 0 + 0,5) + 1] =

= 0,6•0,92 + 0,4• 0,69 = 0,55 + 0,28 = 0,83.

Выражение в круглых скобках под знаком логарифма представляет собой

прирост средств на счете фирмы, равный начальнуму количеству средств на

счете минус инвестиции в проект плюс выручка от реализации проекта плюс

компенсация потерь, гарантированная страховой компанией. При первом ис-

ходе нет потерь, поэтому компенсации 0 руб., при втором исходе потери 0,5 млн

руб. полностью покрываются.

Вычислим стоимостную оценку прибыльности проекта, эквивалентную

его ожидаемой полезности в случае страхования:

0,83 = ln(x

´ + 1) → x´= e

0,83

–1 = 1,29 млн руб.

Руководство фирмы приобретет страховку, если ее стоимость будет удо-

влетворять условию:

1,29 млн руб. — P > 1,03 млн руб., где P — цена страхового полиса. Отсюда

P < 0,26 млн руб.

Получатся, что цена страхового полиса должна быть менее 260 тыс. руб.

Ïîïðàâêà íà ðèñê ïðè îöåíêå ýôôåêòèâíîñòè ïðîäîëæèòåëüíûõ

âî âðåìåíè èííîâàöèîííûõ ïðîåêòîâ. Рассмотрим теперь задачу об

оценке экономической эффективности среднеG и долгосрочных ин-

новационных проектов.

Для оценки эффективности любого инвестиционного проекта рас-

считывают величину NPV (Net Present Value) — так называемую чистую

приведенную стоимость проекта:

, (8)

где B

, C

— величина выручки и затрат в году t; Ñ

— затраты на запуск проекта

(цена участия в проекте, начальные инвестиции в проект и др.); r

— коэффи-

циент дисконтирования для периода 1 ... t реализации проекта (например, r

—

банковская процентная ставка для трехлетнего вклада); t = 1, 2, 3, … — этапы

реализации проекта (годы).

Раздел III. ИННОВАЦИОННЫЕ РИСКИ

122

Формула (8) позволяет рассчитать прибыль, которую принесет про-

ект на текущий момент — год, когда нужно осуществить инвестиции

на запуск проекта. Первый член разности в этой формуле называют

приведенной стоимостью проекта. По смыслу она показывает, сколько

сегодня стоит альтернативный проект (например, банковский вклад)

с заранее известной годовой нормой рентабельности r (скажем, уста-

новленной банком процентной ставкой по вкладу), который в течение

того же периода t будет приносить ту же прибыль Ï

= B

– C

, что и

проект, предлагаемый к рассмотрению. Основной вопрос, который в

данном случае решается: существует ли аналогичный по доходности

и срокам альтернативный проект, который при пересчете на текущий

момент стоит дешевле? То есть можно ли, не участвуя в предлагаемом

к рассмотрению проекте, вложить деньги так, чтобы при тех же бу-

дущих доходах начальных затрат потребовалось меньше? Если такой

альтернативный проект существует, рассматриваемый проект следует

признать неэффективным.

В качестве периода t может фигурировать не только год, но и любой

другой, выбранный исходя из отдельных соображений период контроля

доходности проекта. В качестве альтернативного проекта наиболее

часто рассматривается вложение денег в банк.

Далее необходимо соотнести полученную величину приведенной

стоимости (пересчитанные на текущий момент будущие доходы) с на-

чальными затратами, которые требуются для запуска рассматриваемого

инвестиционного проекта, — Ñ

. Разница между приведенной стои-

мостью, характеризующей альтернативный рассматриваемому проекту

способ вложения денег, и начальными инвестициями, требуемыми для

запуска рассматриваемого инновационного проекта, представляет со-

бой чистую приведенную стоимость проекта. Ее величина показывает,

является ли данный проект более эффективным по сравнению с су-

ществующими альтернативами. Если NPV > 0, то проект более при-

влекателен, чем рассмотренная альтернатива, и инвестировать следует;

если NPV = 0, то имеет место ситуация равноприоритетности проектов

(например, все равно — инвестировать в проект или нести деньги в

банк). Наконец, если NPV < 0, то это означает, что проект не является

инвестиционноGпривлекательным по отношению к рассмотренной

альтернативе.

Теперь уточним формулу чистой приведенной стоимости для слу-

чая инновационного проекта, который обычно характеризуется повы-

шенной рискованностью. В данном случае имеем дело не с точно из-

вестной прибыльностью по этапам t реализации проекта Ï

= B

–C

а с некоторым вероятностным распределением прибыли. Поэтому в

Глава 6. Неопределенность и риск в инновацияХ 123

формуле (8) необходимо перейти от строгих величин к ожидаемым:

NPV

→ NPV

texp

, B

→ B

texp

и C

→ C

texp

(параметры Ñ

и r являются

экзогенными — задаваемыми извне и потому заведомо известными и

строго определенными).

Если вероятностное распределение выручки или затрат в те или

иные периоды спрогнозировать трудно, риск может быть учтен за

счет перехода от безрискового коэффициента дисконтирования r к

коэффициенту дисконтирования r* > r, скорректированного с учетом

риска (надбавка, связанная с дополнительным риском, принимаемым

на себя инвестором). Тем самым требования к оценке эффективности

для инновационных проектов становятся существенно более жест-

кими. Увеличение r приводит к занижению приведенной стоимости

рассматриваемого проекта по отношению к существующим альтерна-

тивам, и, значит, фирма, предлагающая потенциальным инвесторам

участвовать в своем инновационном проекте, должна либо снижать

размер запрашиваемых начальных инвестиций Ñ

, либо тем или иным

способом доказывать инвесторам свою надежность, деловую порядоч-

ность и т.д., чтобы снизить оценку величины r инвесторами (или иными

принимающими решение субъектами).

Следует заметить, что четких правил, по которым осуществляется

переход от величины r к r*, не существует. Соответствующая добавка Δ r

к безрисковому коэффициенту дисконтирования r, которая часто на-

зывается премией за риск (Δ r = r* –r ), может достигать довольно

больших значений (до 7–10% и более), если проект расценивается как

слишком рискованный (например, фирма, осуществляющая проект,

мало известна на рынке или имеет неустойчивую репутацию, либо

слишком трудно предсказать исход НИОКР, которые необходимо

провести, и т.д.). В общем случае назначение премии за риск является

субъективным выбором инвестора, при котором учитывается очень

широкий спектр факторов — от склонности к риску самого инвестора

до стабильности и эффективности национальной инновационной си-

стемы страны, в которой реализуется проект.

Итак, с учетом сделанных замечаний для оценки эффективности ин-

новационного проекта можно использовать следующую формулу:

(9)

где B

t exp

— ожидаемые величины выручки и затрат в году t ;

r* = r + Δ r — коэффициент дисконтирования, увеличенный с учетом

степени рискованности проекта.

Раздел III. ИННОВАЦИОННЫЕ РИСКИ

124

Во избежание завышенных оценок риска расчеты NPV иногда це-

лесообразно проводить с помощью формулы отдельно (9), вводя в нее:

1) только надбавки к коэффициенту дисконтирования; 2) только ожи-

даемые величины выручки и затрат. Данный метод может применяться

и в более сложных и уточненных модификациях

Возможен и несколько иной подход к оценке перспективности про-

екта, который может применяться в случае, когда, например, необходимо

оценить сравнительную эффективность нескольких инновационных про-

ектов или несколько сценариев одного и того же проекта. Для этого

рассчитывают внутреннюю норму рентабельности каждого проекта,

которая определяется из условия

NPV (r)=0. (10)

Теперь в функции NPV = NPV(Ï, Ñ

, r) следует предположить за-

данными и неизменными характеристиками проекта и прибыльность

проекта за период Ï = B – C и необходимые начальные затраты на

запуск проекта Ñ

. Переменной же, напротив, становится величина

r, которая имеет уже иной, чем в формуле (9), смысл. Это уже не эк-

зогенная величина, характеризующая прибыльность альтернативного

проекта, а характеристика данного конкретного проекта, которая по-

казывает, насколько эффективен проект и оправданны ли требуемые

сегодня вложения в него.

Величина r, удовлетворяющая условию (10), и будет внутренней

нормой рентабельности проекта. Выбирается тот проект или тот из его

сценариев, при котором внутренняя норма рентабельности выше.

Рассмотрим типовую задачу. Неизвестная на рынке новообразованная

фирма предлагает инвесторам участие в двухлетнем проекте, который обещает

следующий вероятный уровень прибылей в каждом году (см. таблицу).

Показатель

Год

1-й 2-й

Прибыль, млн. руб. 50 100 100 200

Вероятность получения

такой прибыли

0,5 0,5 0,6 0,4

У потенциальных инвесторов также существует возможность положить

деньги в банк под 5% годовых вместо того, чтобы вложить их в предлагаемый

проект. На какой минимальный размер инвестиций может рассчитывать фир-

ма, предлагающая на рынке свой проект, если местные инвесторы работают с

только вышедшими на рынок фирмами, исходя из премии за риск 7%?

Глава 6. Неопределенность и риск в инновацияХ 125

Решение

Ожидаемая прибыль за 1Gй год реализации проекта: Ï

= 25 + 50 =

=75 млн руб.

Ожидаемая прибыль за 2Gй год реализации проекта: Ï

= 60 + 80 = 140

млн руб.

Предлагаемый проект будет привлекателен для инвесторов в случае, если

NPV > 0.

Однако фирма, которая предлагает свои услуги, на рынке еще никак не успела

себя проявить, поэтому проект является высокорискованным и в расчетах следует

перейти к рисковому коэффициенту дисконтирования: r = 5 + 7 = 12%.

Тогда должно выполняться условие:

75 / (1 + 0,12)

+ 140 / (1 + 0,12)

– Ñ

> 0, отсюда: Ñ

< 66,9 + 111,6 =

=178, 5 млн руб.

Фирма может запрашивать размер начальных вложений, не превышаю-

щий 178,5 млн руб, в противном случае инвесторам будет выгоднее поместить

деньги в банк.

Ñöåíàðíîå ìîäåëèðîâàíèå ðèñêîâûõ ñèòóàöèé

Рассмотрим еще один класс задач по оценке проектных рисков.

Часто бывает необходимым, воGпервых, просчитать несколько вариантов

возможных действий (стратегий управления или сценариев развития

проекта) и, воGвторых, учесть разнообразные ситуации, которые могут

возникать во внешней среде и делать более или менее приоритетными

те или иные стратегии. Решение подобного класса задач предполагает

использование аппарата теории игр.

Пусть {A

}

, i

= 1,..., N, — набор стратегий (сценариев), которые

могут быть реализованы командой проекта (фирмой, предпринима-

телем и т.д.). Пусть {B

}

, i

= 1,..., M, — набор возможных состояний

внешней среды, в которой развивается проект. И наконец, пусть {Ï

} —

прибыль, которую принесет проект при реализации iGй стратегии и

jGм состоянии внешней среды. Математически подобную ситуацию

отражает матрица, которую называют платежной:

А =

... В

...

2М

...

(11)

Раздел III. ИННОВАЦИОННЫЕ РИСКИ

126

Задача состоит в том, чтобы определить: 1) оптимальную стра-

тегию при тех или иных предположениях о вероятности реализации

различных состояний внешней среды; 2) размер прибыли, который

принесет проект при выбранной стратегии; 3) ущерб или упущенные

возможности, возникающие в связи с несовершенством информации

о состоянии внешней среды (о действиях конкурента, потребительских

предпочтениях и др.).

Здесь возможны разные подходы в зависимости от того, какие допу-

стимо сделать предположения о свойствах внешней среды (например,

о характере институтов, действующих правилах, регулирующих про-

цедурах), и от полноты информации, которой мы располагаем (напри-

мер, известна нам стратегия конкурента или нет). ДавольноGтаки часто

решение подобных задач оказывается весьма сложным и трудоемким.

Здесь ограничимся только некоторыми частными случаями.

В первую очередь рассмотрим ситуацию, близкую к ситуации не-

определенности, когда нам известны возможные состояния внешней

среды {B

}, но ничего не известно о вероятностях, с которыми то или

иное состояние реализуется. Существует целый набор критериев, ко-

торыми в этом случае может руководствоваться команда проекта при

выборе бизнесGстратегии или сценария реализации проекта. В табл. 6.1

приведены критерии, наиболее часто используемые на практике

Òàáëèöà 6.1

Êðèòåðèè ïðèíÿòèÿ ðåøåíèé â óñëîâèÿõ âåðîÿòíîñòè

íåîïðåäåëåííîñòè ñîñòîÿíèé âíåøíåé ñðåäû

Наименование критерия Примечание

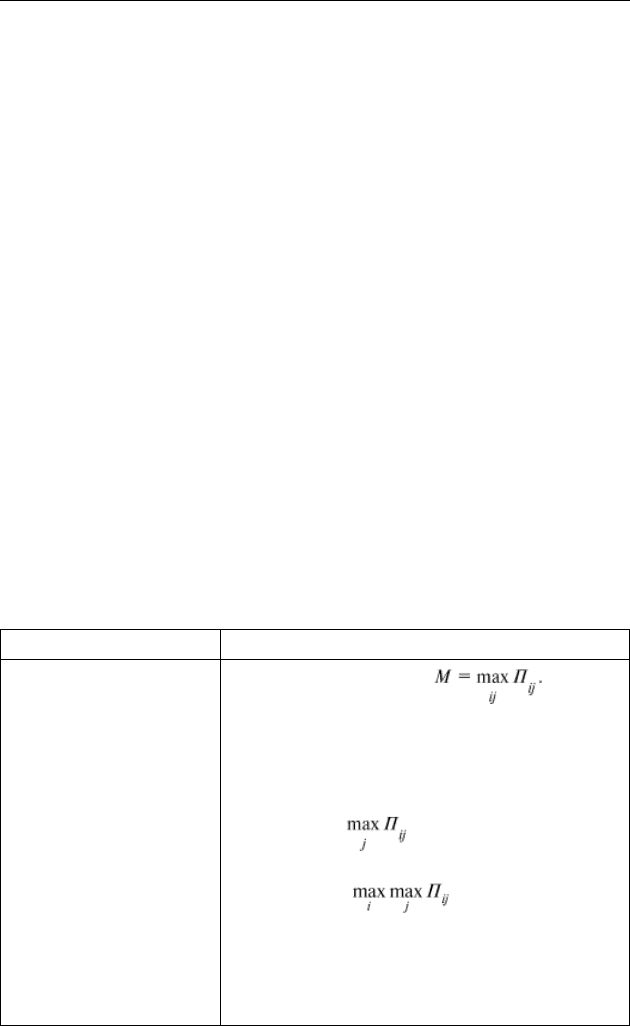
Оптимистический

критерий

Математическая запись: При этом

критерии предполагается, что нам будет везти,

поэтому: 1) для каждой стратегии A

выбирает-

ся наилучшее состояние внешней среды B, при

котором размер прибыли является наибольшим

(т.е. находится ); 2) из полученного на 1-м

шаге ряда значений П

выбирается максимальное

(т.е. находится ), а соответствующая

стратегия A

рассматривается как оптимальная.

Критерий позволяет вычислить максимально воз-

можную прибыль проекта, но она будет гаранти-

рована только в том случае, если ситуация будет

развиваться исключительно в нашу пользу

Глава 6. Неопределенность и риск в инновацияХ 127

Ïðîäîëæåíèå òàáë. 6.1

Наименование

критерия

Примечание

Критерий недостаточно-

го основания (критерий

Лапласа)

Математическая запись:

, где

М — число возможных состояний внешней среды.

Критерий предполагает, что вероятности реали-

зации всех состояний внешней среды равны. На

основе этого предположения сначала для каждой

стратегии А

вычисляется среднее арифметическое

значение прибыли, а затем выбирается макси-

мальное из них. Критерий работает оптимально,

если реальная ситуация позволяет реализовать

стратегию большое количество раз, т. е. необхо-

димо максимизировать выигрыш не одномомент-

но, а на определенном интервале времени

Пессимистический

критерий - 1

(критерий Вальда)

Математическая запись:

. При

этом критерии предполагается, что нам бу-

дет тотально не везти, поэтому: 1) для каждой

стратегии A

выбирается наихудшее состояние

внешней среды B

, при котором размер прибыли

является наименьшим (т. е. находится );

2) из полученного на 1-м шаге ряда значений

выбирается максимальное (т. е. находит-

ся ), а соответствующая стратегия

рассматривается как оптимальная. Критерий

позволяет вычислить нижнюю границу прибыли,

т. е. величину, ниже которой прибыль гарантиро-

ванно не упадет. Критерий хорошо работает, ког-

да решение нужно принять один- единственный

раз и нет возможности экспериментировать. Од-

нако, реализуя такой сценарий, можно упустить

более высокую прибыль, которая окажется воз-

можной, если будет иметь место не самое худшее

(как предполагали) состояние внешней среды

Раздел III. ИННОВАЦИОННЫЕ РИСКИ

128

Îêîí÷àíèå òàáë. 6.1

Пессилистический

критерий-2 (критерий

Сэвиджа)

Математическая запись: . Этот

критерий полностью идентичен предыдущему, с

той лишь разницей, что мы имеем дело не с ма-

трицей прибылей, а с матрицей рисков, элементы

которой могут иметь смысл ущерба, который

грозит проекту при различных комбинациях стра-

тегий фирмы и состояний внешней среды, или

упущенных возможностей, связанных с неполно-

той информации при принятии решений. В по-

следнем случае может использоваться следующая

связь между r и П:

Композитный (критерий

Гурвица)

Математическая запись:

Данный критерий является суперпозицией

оптимис-тического и пессимис-тического крите-

риев. Все зависит от того, насколько команда про-

екта считает возможным полагаться на везение.

C этой целью в расчеты вводится коэффициент p

(0 ≤ p ≤ 1). При p = 0 реализуется оптимистиче-

ский критерий, при p = 1 — пессимистический.

Коэффициенты p и (1–p) характеризуют соот-

ветственно степени пессимизма и оптимизма

игроков.

Возможна и другая ситуация, когда известным оказывается не

только набор состояний внешней среды, но и вероятности, с ко-

торыми каждое из состояний может реализоваться. В этом случае

имеем информацию не только о наборе {B

}, но и о множестве пар

, p

}, где p

— вероятность реализации jGго состояния внешней среды.

Информация об этих вероятностях может быть получена различными

способами, наиболее распространенным из которых на практике яв-

ляется экспертиза. Экспертами сначала идентифицируются, а затем

взвешиваются факторы риска (определяется вероятность состояний

внешней среды). Эта процедура осуществляется на этапе качественного

анализа рисков, о котором подробно говорилось в пункте «Основные

этапы качественной оценки рисков» настоящей главы .

Глава 6. Неопределенность и риск в инновацияХ 129

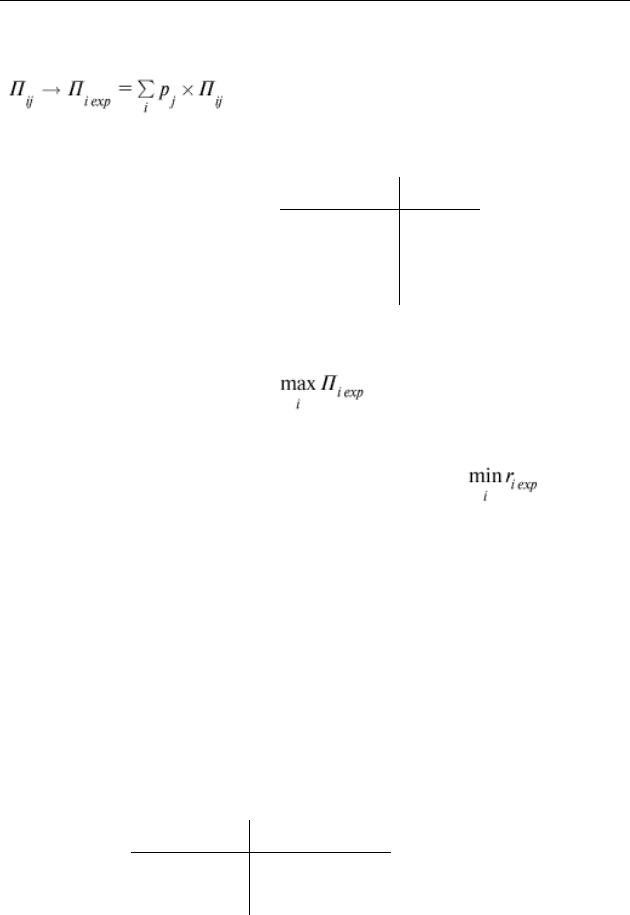
В рассматриваемом случае для выбора оптимальной страте-

гии, в матрице (11) необходимо перейти к ожидаемым величинам

( ), получив столбец Ï

i exp

, который ставит

в cоответствие каждой стратегии A

величину ожидаемой прибыли

(см. матрицу 12).

А =

i exp

...

1 exp

2 exp

...

N exp

Далее следует выбрать ту стратегию, которая соответствует макси-

мальной ожидаемой прибыли ( ). Если изначально использо-

валась не матрица прибылей, а матрица рисков, необходимо проделать

аналогичные действия, с той лишь разницей, что выбор стратегии дол-

жен удовлетворять условию минимизации ущерба ( ).

Состояния внешней среды могут моделироваться поGразному,

например иметь иерархическое строение, когда разные состояния

приводят к возможности реализации новых наборов состояний и т.д.

В этом случае мы получаем так называемое «дерево» решений, каждая

ветвь которого представляет собой одну из возможных альтернатив

(сценариев). Выбор оптимального решения осуществляется посред-

ством последовательного отбрасывания менее перспективных ветвей,

а перспективность каждой ветви определяется с помощью описанного

выше алгоритма.

Рассмотрим типовую задачу. Пусть {A

} — набор возможных стратегий

фирмы À; {B

} — возможные состояния рынка. Дана матрица прибылей фирмы

À (млн руб.) при различных состояниях рынка:

Определить:

1) оптимальную стратегию фирмы À в соответствии с пессимистическим

критерием Вальда;

(12)