Лабораторные работы по курсу общей физики (3-я Редакция 2012 г.)
Подождите немного. Документ загружается.


- 3 -
Для равновесного адиабатического процесса справедливо уравнение Пуассона:
7) pV
= const, где - коэффициент Пуассона (показатель адиабаты).
Используя уравнение Менделеева-Клапейрона, можно из уравнения Пуассона найти связь
между р и Т, а также V и Т в адиабатическом процессе:
8)
constpT
1
,
constVT
1
1
.
9)
1
V
p
V
p
C
C
C
C
, где С
p
- молярная и С
p
-
удельная теплоемкости при постоянном
объеме, С
р
и С
р
- молярная и удельная
теплоемкости при постоянном давлении.
На рис. 1 сплошная кривая - адиабата - изображает в
p-V-диаграмме адиабатический процесс, а
штриховая линия - изотерма - изотермический про-
цесс при температуре, соответствующей начальному
состоянию 1 газа. При адиабатическом процессе
давление меняется с изменением объема газа резче,
чем при изотермическом процессе. При
адиабатическом расширении уменьшается температура газа и его давление падает быстрее,
чем при соответствующем изотермическом расширении. При адиабатическом сжатии газа его
давление возрастает быстрее, чем при изотермическом сжатии. Это связано с тем, что
увеличение давления происходит за счет уменьшения объема газа и в связи с возрастанием
температуры. Работа А
1-2
, совершаемая газом при адиабатическом процессе 12, измеряется
площадью, заштрихованной на рис. 1.
Распространение звуковой волны в газе (воздухе) происходит адиабатически, так как сжатия и
разрежения в газе сменяют друг друга настолько быстро, что теплообмен между слоями газа,
имеющими разные температуры, не успевает произойти. Такие процессы описываются
уравнением (7). Известно, что скорость распространения звуковой волны в газах зависит от
показателя адиабаты . Скорость звука в газах определяется формулой:
10)
RT
, где R - универсальная газовая постоянная, Т - температура газа,
- молярная
масса газа.
Преобразуя формулу (10), находим:
11)
2
RT
.
Таким образом, для определения показателя адиабаты достаточно измерить температуру газа
и скорость распространения звука (молярная масса предполагается известной - для воздуха
=29-10
-3
кг/моль).
Звуковая волна, распространяющаяся вдоль трубы, испытывает многократные отражения от
торцов. Звуковые колебания в трубе являются наложением всех звуковых волн и довольно
сложны. Картина упрощается, если длина трубы L равна целому числу длин полуволн, т.е.
когда
12)
2
nL
, где
- длина волны звука в трубе; п - любое целое число.
Если условие (12) выполнено, то волна, отраженная от торца трубы, вернувшаяся к ее началу
и вновь отраженная, совпадает по фазе с падающей. При звуковых колебаниях слои воздуха,
прилегающие в торцам трубки, не испытывают смещения (узел - смещения). Узлы смещения
повторяются по всей длине трубы через
2
. Между узлами находятся максимумы смещения
(пучности).
Рис. 1
- 4 -
Скорость звука
связана с его частотой
и длиной волны
соотношением:
13)
.
Длина волны может быть найдена из соотношения:
17)
2
nL
n
где L
n
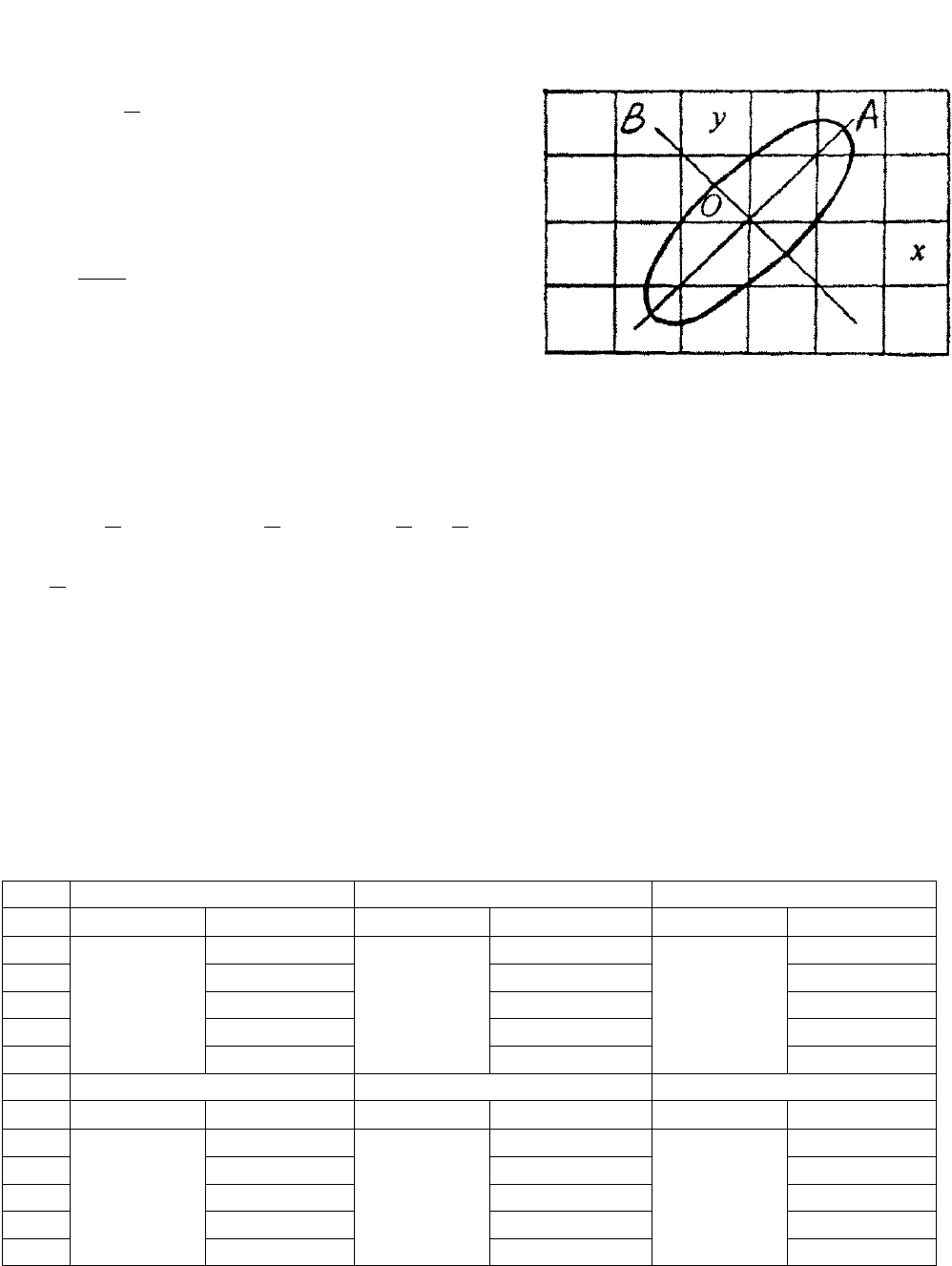
- расстояние между n
положениями телефона и микрофона, в которых
эллипс последовательно вырождается в прямые А и
В (рис. 2).
С учетом формулы (13) имеем:
18)
n
vL
n
2
.
При неизменной частоте
звукового генератора (и,
следовательно, неизменной длине звуковой волны
) можно изменять расстояние L
n
между
телефоном и микрофоном. Для этого микрофон или телефон приближаются или удаляются
друг от друга с помощью специального стержня на установке. Данный стержень градуирован
шкалой, цена деления которой 510
-5
м. Наблюдая положения, в которых эллипс вырождается
в прямую, имеем:
19)
2
nL
n
,
22
,...,
2
)1(
1
knLnL
knn
,
т.е.
2
равно угловому коэффициенту графика, изображающего зависимость L
n
от номера
положения п. Скорость звука находится по формуле (13), а отношение удельных
теплоемкостей рассчитывается по формуле (11).
Расчётная часть
После снятия показаний с установки получаем 3 серии измерений. Каждой серии
соответствует своё значение частоты звуковой волны
. Для большей достоверности
измерений, измерения каждой серии сняты для двух случаев: а) - микрофон движется по
направлению от телефона; б) - микрофон движется по направлению к телефону.
а)
серия 1
серия 2
серия 3
n
1
, Гц 10
3
L
n
, м
2
, Гц 10
3
L
n
, м
3
, Гц 10
3
L
n
, м
1
3,52
0,100
3,62
0,100
3,768
0,100
2
0,137
0,134
0,134
3
0,186
0,183
0,180
4
0,235
0,230
0,225
5
0,285
0,280
0,272
б)
серия 1
серия 2
серия 3
n
1
, Гц 10
3
L
n
, м
2
, Гц 10
3
L
n
, м
3
, Гц 10
3
L
n
, м
1
3,52
0,100
3,62
0,100
3,768
0,100
2
0,136
0,134
0,133
3
0,185
0,182
0,180
4
0,235
0,229
0,225
5
0,285
0,280
0,272
Снятия показаний проводились при стандартных условиях т.е. температура воздуха в трубке
T примем равной 20 C (T = 293 K).
При произведении вычислений для каждой серии будут использоваться средние
арифметические значения соответствующих значений длин L
n
взятые из а) и б) частей
Рис. 2
- 5 -
таблицы. Для удобства результаты L
n
для случая б) записаны в соответствии с номерами
результатов n в части таблицы а).
Для нахождения длины звуковой волны (
) испускаемой телефоном, построим для каждой
серии графики зависимости L
n
от n. Значения L
n
возьмём усреднённые, как описывалось выше.
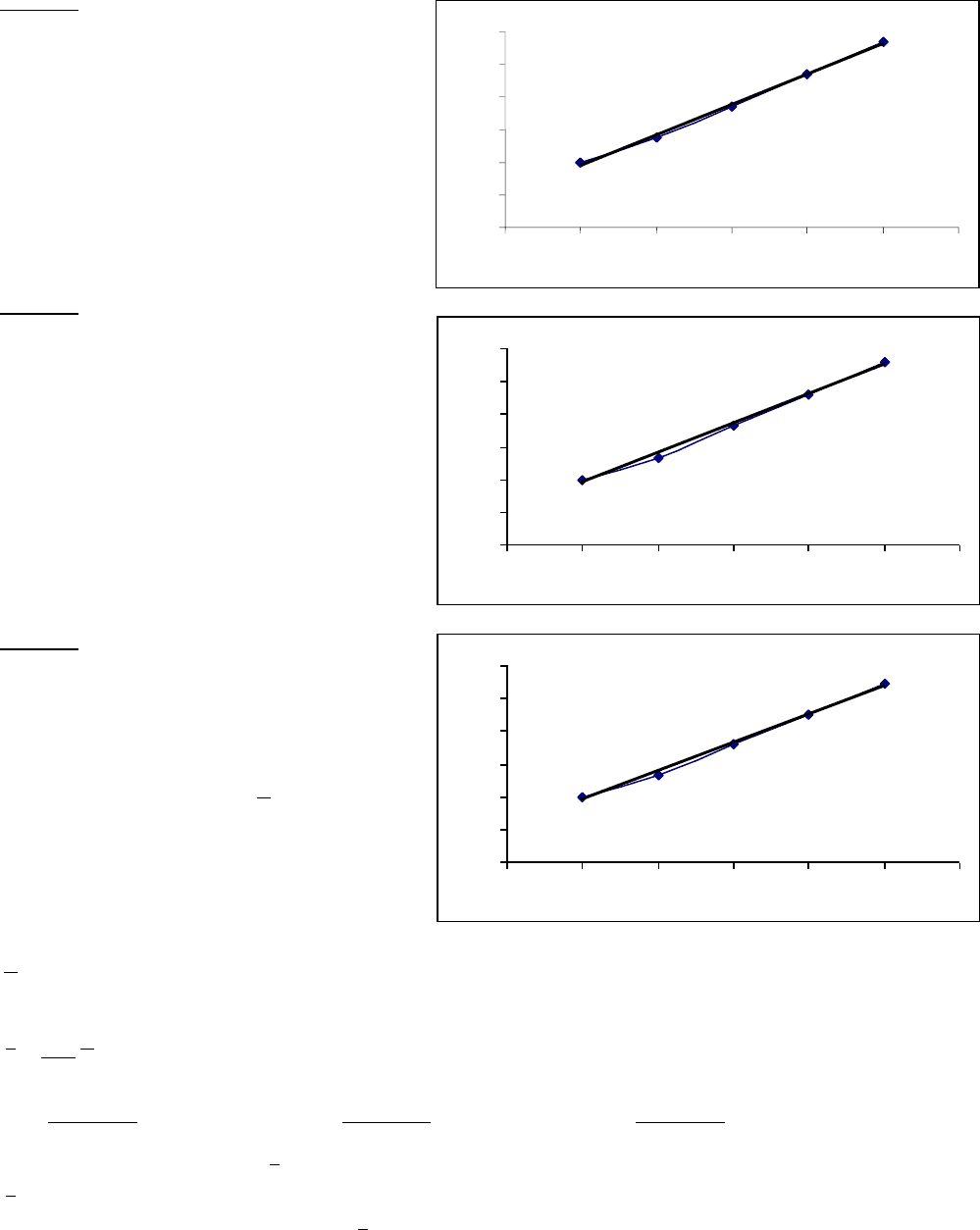
Серия 1.
Примерное значение коэффициента
наклона данного графика можно
получить после его аппроксимации
(усреднению квадратов значений
координат точек). т.е. L
n
= 0,0469n.
Подставим L
n
из данного выражения в
формулу (17), получим, что:
1
/2 = 0,0469, отсюда
1
= 20,0469 =
= 9,3810
-2
м.
Серия 2.
Данный график с расчётами построим
аналогично предыдущему графику.
L
n
= 0,0456n. Отсюда:
2
= 9,1210
-2
м.
Серия 3.
Точно так же строится график и для
третьей серии измерений.
L
n
= 0,0436n. Отсюда:
3
= 8,7210
-2
м.
Далее вычислим действительное
значение скорости звука
через
1
,
2
и
3
, найденные по формуле (13):.
18,330103,52109,38
32
1
м/с.
14,330103,62109,12
32
2
м/с.
57,328103,768108,72
32
3
м/с.
63,329
м/с.
Теперь, для каждого значения частоты по формуле (11) найдём показатель адиабаты
.
2
RT
;
23,118,330
29331,8
1029
2
3
1
;
23,114,330
29331,8
1029
2
3
2
;
29,1327,57
29331,8
1029
2
3
3
;
Действительное значение
найдём, как среднее арифметическое от
1
,
2
и
3
:
25,1
.
Остаётся вычислить погрешность
. Так, как
находится из простой линейной формулы, то
для нахождения абсолютной погрешности можно использовать упрощённую формулу вида:
0,1
0,1365
0,1855
0,235
0,285
y = 0,0469x
0
0,05
0,1
0,15
0,2
0,25
0,3
0
1
2
3
4
5
6
L
n
n
0,1
0,134
0,1825
0,2295
0,28
y = 0,0456x
0
0,05
0,1
0,15
0,2
0,25
0,3
0 1 2 3 4 5 6
n
L
n
0,1
0,1335
0,18
0,225
0,272
y = 0,0436x
0
0,05
0,1
0,15
0,2
0,25
0,3
0 1 2 3 4 5 6
L
n
n

- 6 -
, где
22
4
n
LT
при
2
22
4
RTn
vL
n
.
Так, как относительная погрешность величин находится последующей формуле:
T
T
T
, то
найдём абсолютную погрешность T. В силу того что температура была замерена однократно
то за значение абсолютной погрешности принимают значение её случайной составляющей.
Tсл
T
;
2
c
k
Tсл
; при k = 1,1 и c = 1.
2
1075,2
2932
1,1
T
.
При вычислении L
n
за действительное значение L
n
примем среднее арифметическое значение
всех 30-ти измерений ((а) и (б) частей всех серий), при c = 10
-3
м.
3
3
103
2
101,1
n
L
.
Возвращаясь к формуле вычисления
, подставим получившиеся значения T и L
n
.
294
1044,310361056,725,1
Итого получаем:
= (125 3,44)10
-2
.

- 1 -
Министерство образования РФ
Рязанская государственная радиотехническая академия
Кафедра ОиЭФ
Лабораторная работа № 1-11
«ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ ПРИ ПОМОЩИ
ОБОРОТНОГО И МАТЕМАТИЧЕСКОГО МАЯТНИКОВ»
Выполнил ст. гр. 255
Ампилогов Н. В.
Проверил
Малютин А. Е.
Рязань 2002
- 2 -
Цель работы: изучение законов колебания маятника; ознакомление с косвенными
методами измерения ускорения свободного падения при помощи математического и
оборотного маятников.
Приборы и принадлежности: маятник универсальный ФПМ-04 (далее - маятник).
Элементы теории
Наиболее точные измерения ускорения свободного падения g выполняются с помощью
косвенных методов. Многие из них основаны на использовании формулы для периода
колебаний физического маятника. Массу маятника и период его колебаний можно
измерить с очень высокой точностью, но точно измерить момент инерции не удается.
Указанного недостатка лишен метод оборотного маятника, который позволяет
исключить момент инерции из расчетной формулы для g.
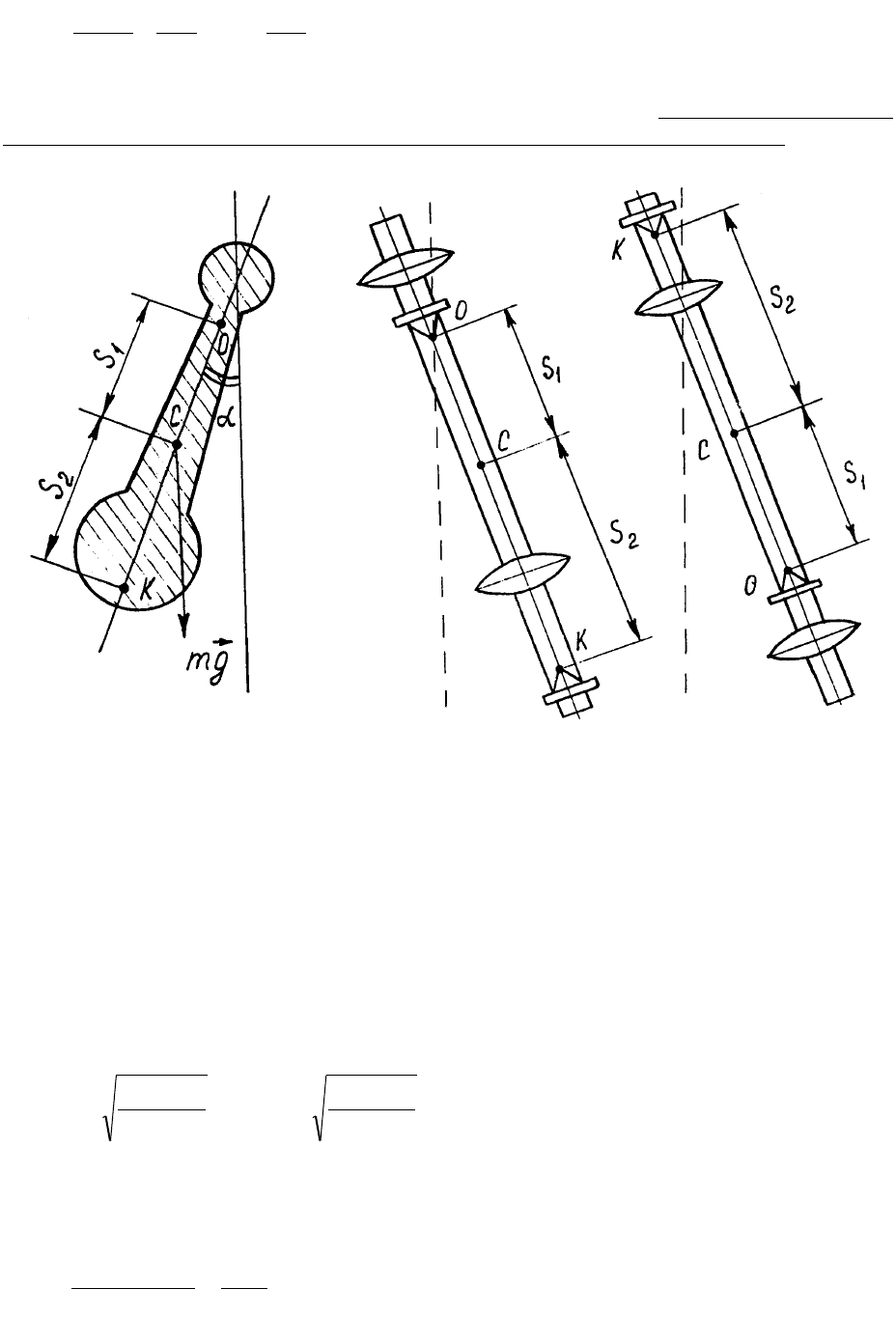
Рассмотрим тело массы m, способное колебаться относительно точки О и отклоненное от
положения равновесия на угол а (рис. 1). Это тело представляет собой физический
маятник с моментом инерции I (относительно оси О, перпендикулярной плоскости
рисунка).
Приведенная длина физического маятника l - это длина такого математического
маятника, период колебаний которого равен периоду колебаний данного физического
маятника:
(1)
g
l
mgS
I
T
22
1
;
Отсюда
1
mS
I
l
, где I - момент инерции маятника относительно оси качаний, т - его масса, S
1
-
расстояние от центра масс до точки подвеса.
Измерить приведенную длину можно перераспределением масс маятника или
изменением положения точки его подвеса.
Точка К, лежащая на перпендикуляре к оси качаний, проходящем через центр тяжести
физического маятника на расстоянии l от этой оси, называется центром качаний
(математический маятник длины l, подвешенный к оси качаний физического маятника,
будет колебаться синхронно с центром качаний).
Приведенная длина маятника
2)
1
1
mS
I
l
.
По теореме Штейнера
3)
1
1
0
1
2
10
1
S
mS
I
mS
mSI
l
.
Если заставить маятник колебаться около горизонтальной оси, проходящей через К, его
приведенная длина
4)
2
2
0
2
2
20
2
S
mS
I
mS
mSI
l
, где S
2
=KC - расстояние от новой оси вращения до центра
масс маятника; I
0
-момент инерции относительно оси, перпендикулярной плоскости
рисунка и проходящей через центр масс маятника. Из рис. 1 следует, что
5)
1
0
112
mS
I
SlS
.
Подставим это выражение в формулу (4) и найдем приведенную длину l
2
:
- 3 -
6)
1
1
0
1
1
0
0
10
2
l
mS
I
S
mS
I
mI
mSI
l
.
Таким образом, центр качаний обладает следующим свойством: если ось пройдет через
центр качаний, то новый центр качаний будет расположен на месте старой оси.
Из равенства приведенных длин следует равенство периодов колебаний.
Оборотным маятником называется физический маятник, центр качаний которого
расположен в пределах колеблющегося тела. Такой маятник можно подвешивать в
любой из двух точек О и К (рис. 2) без изменения периода колебаний: T
1
=T
2
=T.
Взаимозаменяемые точки О и К расположены по обе стороны от центра масс С на
расстояниях S
1
и S (рис. 2). Моменты инерции относительно осей, проходящих через эти
точки, различны:
7) I
l
=I
0
+mS
1
и I
2
=I
0
+mS
2
.
Периоды колебаний оборотного маятника могут быть выражены:
8)
1
2
10
1
2
mgS
mSI
T
и
2
2
1
2
20
2
mgS
mSI
T
.
Учитывая равенство периодов, и решая эту систему уравнений, легко получить
выражение для ускорения свободного падения:
9)
2
2
2
21
2
4
)(4
T
l
T
SS
g
, где l = S
1
+ S
2
- приведенная длина маятника.
Рис. 1
Рис. 2
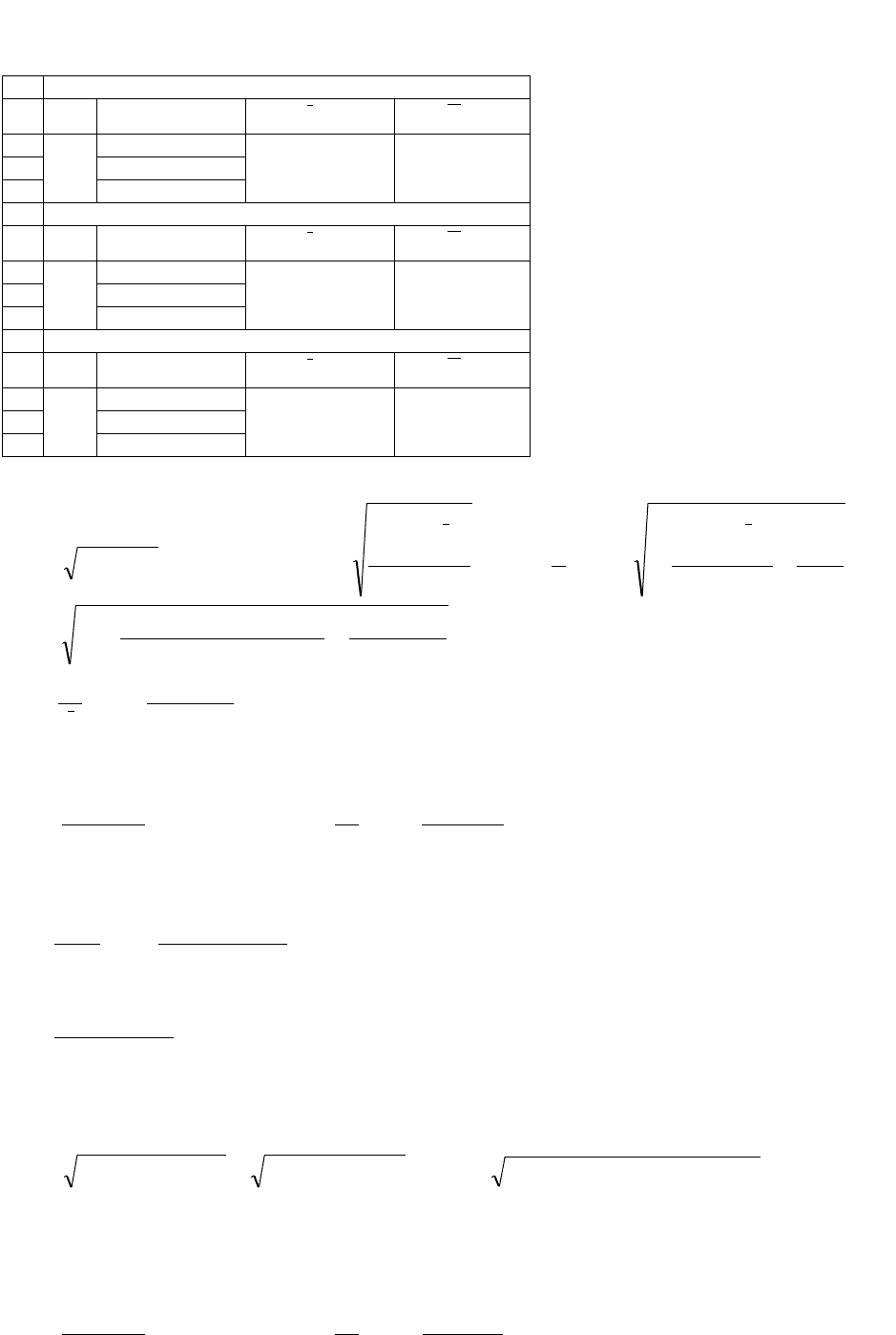
- 4 -
Расчётная часть
l = 0,39 м. (расстояние между
крепёжными призмами);
l = 0,4 м. (расстояние между
крепёжными призмами);
l = 0,37 м. (длина подвеса
маятника);
Вначале рассчитаем погрешность измерения времени t, при c = 10
-3
с, k = 1,1 и t
c
= 4,3:
;
22
ссл
t
;
слcсл
t
;
)1(
)(
2
1
nn
tt
n
i
i
сл
;
2
c
k
с
;
4)1(
)(
22
2
1
2
ck
nn
tt
tt
n
i
i
c
1
6222
2
1055,1
4
1021,1
6
07,002,005,0
3,4
t
с.
;
t
t
t
;1021,6
94,24
1055,1
3
1
t
Вычислим погрешность однократного (
сл
= 0) измерения величины l для физического
маятника, при c = 10
-2
м.:
3
2
105,5
2
101,1
l
м.
;
l
l
l
;1053,1
36,0
105,5
2
3
l
Теперь по формуле 0(9) подсчитаем значение g по данным снятым с физического
маятника (а):
2
2
4
T
l
g
;
84,9
25,1
39,014,34
2
2
g
м/с
2
.
Далее подсчитаем значение g по данным снятым с физического маятника (б):
78,9
27,1
4,014,34
2
2
g
м/с
2
.
Вычисления с физическим маятником завершим вычислением (по упрощённой формуле)
погрешности косвенной величины g. За относительную погрешность периода колебаний
T, примем относительную погрешность измерения времени t:
22
2
22
2
22 ltlTg
;
194,01053,11021,64
4262
gg
м/с
2
Итого для физического маятника получен результат:
g = 9,810,194 м/с
2
.
Вычислим погрешность однократного измерения величины l для математического
маятника, при c = 10
-3
м.:
4
3
105,5
2
101,1
l
м.
;
l
l
l
;1053,1
36,0
105,5
3
4
l
а)
Физический маятник
№
N
t
i
, с
i
t
, с
T
, с
1
20
24,99
24,94
1,25
2
24,96
3
24,87
б)
Физический маятник
№
N
t
i
, с
i
t
, с
T
, с
1
20
25,83
25,6
1,27
2
25,67
3
25,17
Математический маятник
№
N
t
i
, с
i
t
, с
T
, с
1
80
97,89
97,83
1,22
2
97,78
3
97,82

- 5 -
Пользуясь тем же выражением, вычислим значение g по данным снятым с
математического маятника:
8,9
22,1
37,014,34
2
2
g
м/с
2
.
Теперь для математического маятника найдём погрешность величины g:
36262
1021,51053,11021,64
gg
м/с
2
Для математического маятника получен результат:
g = (9800,521)10
-2
м/с
2
.

- 1 -
Министерство образования РФ
Рязанская государственная радиотехническая академия
Кафедра ОиЭФ
Лабораторная работа № 1-16
«ИЗУЧЕНИЕ ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТЕЛА С ПОМОЩЬЮ
МАШИНЫ АТВУДА»
Выполнил ст. гр. 255
Ампилогов Н. В.
Проверил
Малютин А. Е.
Рязань 2002
