Labelle P. Supersymmetry DeMYSTiFied

Подождите немного. Документ загружается.

196

Supersymmetry Demystified

This is simply 4m times the expression we would have in a boson propagator, so

we may write

Tr[S(z − z)] = 4mD(z − z) (9.56)

Equation (9.54) is therefore





(x −w )D

(y − w)D

(z − w)D(z − z)





=−8ig

(9.57)

where once more we have used Eq. (9.44).

Contribution from L

The integral is [see Eqs. (9.39) and (8.71)]



z0|T

B(x)B(y)



B(z)

(z)γ

(z) B(w)(w)γ

(w)

#

|0

(9.58)

Obviously, B(x) must be contracted with either B(w) or B(z), and B(y) must

be contracted with the remaining B. This gives two contributions. We get, after

contracting the B ﬁelds only,



(x − z)D

(y − w)0|T





(z)γ

5αβ



(z) 

(w)γ

5δρ



(w)



|0

(9.59)

where the spinor indices are shown explicitly.

If we contract the two spinors at z with each another and the two spinors at w

with each other, we get a disconnected graph. We therefore must contract the two

spinors at w with the two spinors at z. At this point, we must keep in mind that we

are dealing with Majorana fermions, so we have more possibilities than for a Dirac

CHAPTER 9 Some Explicit Calculations

197

fermion. Keeping this in mind, we get

0|T





(z)γ

5αβ



(z) 

(w)γ

5δρ



(w)



|0

=0|T





(z)γ

5αβ



(z) 

(w)γ

5δρ



(w)



|0

+0|T





(z)γ

5αβ



(z) 

(w)γ

5δρ



(w)



|0 (9.60)

Consider the second term ﬁrst. This is a term we also would get for Dirac

fermions. Recall that in the fermion propagator (9.18), the  appears to the left of

the Dirac conjugate ﬁeld

, so we must move 

(w) to the left of 

(z). Every

time we move a fermion ﬁeld passed a  or a

, we pick up a minus sign, so we get

0|T





(z)γ

5αβ



(z) 

(w)γ

5δρ



(w)



|0

=−0|T





(w)

(z)γ

5αβ



(z)

(w)γ

5δρ



|0 (9.61)

Now we can replace the contractions by fermion propagators, which gives us that

the second term of Eq. (9.60) is ﬁnally equal to

−S

ρα

(w − z)γ

5αβ

βδ

(z − w)γ

5δρ

=−Tr



S(w − z)γ

S(z − w)γ



(9.62)

We obtain a trace of the matrices because all the indices appear next to one another

except for the index ρ, which appears at the very beginning and at the very end.

Let us now turn our attention to the ﬁrst term of Eq. (9.60). This is a contribution

that we would not have if we were considering Dirac fermions. In order to use the

propagators (9.25) and (9.26), we need to move the two  next to one another and

the two

 next to one another as well. In principle, we could use any order between

the two  and between the two

, but the calculation will be much simpler if we

arrange the order so that we get a trace. Unfortunately, we can’t quite make it work.

For example, if we move the



(w) to the left of 

(z) and 

(w) to the right of



(z),weget

0|T





(z)γ

5αβ



(z) 

(w)γ

5δρ



(w)



|0

=0|T





(w)

(z)γ

5αβ



(z)

(w)γ

5δρ



|0 (9.63)

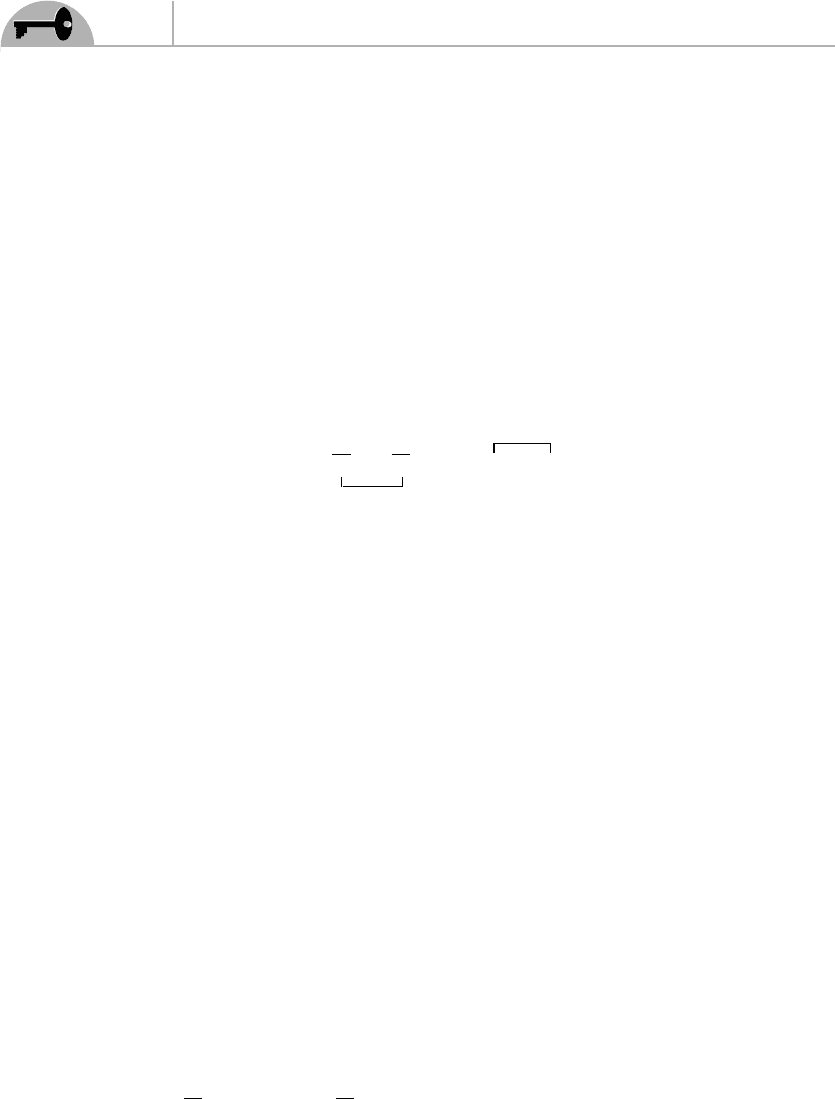
198

Supersymmetry Demystified

We see that the indices are not in order: There is a mismatch because of the indices

of the γ

matrix on the far right. The way out is of course to reverse the indices of

that matrix. This can be done by using the identity (valid for any matrix)

5δρ

= (γ

)

ρδ

(9.64)

However, because γ

= γ

, we see that we are free to switch the order of its indices,

5δρ

= γ

5ρδ

(9.65)

which allows us to write Eq. (9.63) as

0|T





(w)

(z)γ

5αβ



(z)

(w)γ

5ρδ



|0

= C

δγ

γα

(w − z)γ

5αβ

βμ

(z − w)C

μρ

5ρδ

= Tr



S(w − z)γ

S(z − w)C



Now, it turns out that there is always a way to get rid of the C

matrices. The

trick is to use that C

=−C = C

−1

so that (C

)

=−1. In order to use this,

though, we need to get the two C

matrices next to one another. We will do this

in two steps. First, we use the invariance of the trace under cyclic permutations,

Tr(ABC D) = Tr(DABC) to write



S(w − z)γ

S(z − w)C



= Tr



S(w − z)γ

S(z − w)C



(9.66)

Next, we use the fact that γ

and C

commute; i.e., γ

= C

(which can be

easily checked using their explicit representations), so we ﬁnally obtain



S(w − z)γ

S(z − w)C



= Tr



S(w − z)γ

S(z − w)C



=−Tr



S(w − z)γ

S(z − w)γ



(9.67)

which is equal to what we had obtained for the second term of Eq. (9.60) [see also

Eq. (9.62)]. Therefore, Eq. (9.60) is equal to

0|T





(z)γ

5αβ



(z) 

(w)γ

5δρ



(w)



|0=−2Tr



S(w − z)γ

S(z − w)γ



(9.68)

CHAPTER 9 Some Explicit Calculations

199

Figure 9.11 Diagram corresponding to Eq. (9.69). The vertices drawn as a cross inside a

circle represent interactions containing a γ

matrix.

Plugging this back into the expression for the diagram, i.e., Eq. (9.59), we get

that the contribution of L

−2g



(x − z)D

(y − w)Tr



S(z − w)γ

S(w − z)γ



(9.69)

which is shown in Figure 9.11 and corresponds to the integral

−2g



(2π)

−ip·(x−z)

− m

+i 



(2π)

−iq·(y−w )

− m

+i 



(2π)



(2π)



−ik·(z−w )

/k − m +i 

−il·(w−z)

/l − m + i



(9.70)

Doing the integration over z gives a factor (2π)

( p − k +l), which we may

use to integrate over d

l.Weget

−2g



(2π)

−ip·x

− m

+i 



(2π)

−iq·(y−w )

− m

+i 



(2π)

ip·w



/k − m +i 

/k − /p − m + i



(9.71)

Doing the integral over w and then over q,weget



(2π)

−ip·(x−y)

− m

+i 

− m

+i 



(2π)

(/k + m)γ

(/k − /p +m)γ

− m

)[(k − p)

− m

]

200

Supersymmetry Demystified

To carry out the traces, we simply need to use (γ

)

= 1, γ

=−γ

,Tr(/a) = 0,

Tr(/aγ

/bγ

) =−4a · b, and obviously, Tr(1) = 4. This leads us to



(2π)

−ip·(x−y)

− m

+i 

− m

+i 



(2π)

k · p − k

+ m

− m

)[(k − p)

− m

]

(9.72)

This contains a quadratic divergence, but it is not easy to isolate it in that form. A

standard trick is to write the numerator as

k · p − k

+ m

−( p − k)

+ k

+ p

− 2k

+ 2m

−( p − k)

+ m

− k

+ m

+ p

(9.73)

so that the integral is

−4g



(2π)

−ip·(x−y)

− m

+i 

− m

+i 



(2π)

(k − p)

− m

−

− m

)[(k − p)

− m

]

In this form, it is clear that the quadratic divergence is isolated in the ﬁrst two

terms. Ignoring the last term and making the change of variable k → k + p in the

ﬁrst integral, we can ﬁnally see that the quadratically divergent contribution of this

diagram is

−8g





(2π)

−ip·(x−y)

− m

+i 

− m

+i 



(2π)

− m





= 8ig

(9.74)

As an aside, the change of variable we just performed is ﬁne as long as we are only

interested in isolating the quadratic divergent contribution of the diagram. If we

were interested in extracting the ﬁnite contribution, we could not be as cavalier.

CHAPTER 9 Some Explicit Calculations

201

The Remaining Terms

There are still three terms we haven’t calculated: the terms in L

I 3

, L

I 2

I 4

, and

I 3

I 4

. However, none of these terms contribute connected diagrams to the one-

loop B propagator as you can easily verify.

9.5 Putting It All Together

Let us summarize our results. We will group the contributions into two groups:

the tadpole diagrams and the nontadpole diagrams. Our goal is to demonstrate that

quadratic divergences cancel out, so we don’t take into consideration the diagram

of Figure 9.7 which contains a logarithmic divergence.

For the tadpole diagrams, we found

A tadpole = 6ig

B tadpole = 2ig

Fermion tadpole =−8ig

Sum = 0 (9.75)

The results for the nontadpole diagrams are

A loop =−2ig

B loop =−6ig

Fermion loop = 8ig

Sum = 0 (9.76)

As advertised, all quadratic divergences cancel out!

The choice of grouping the contributions into tadpole versus nontadpole diagrams

to show the cancellation may seem arbitrary in this example. For example, we

could have grouped instead the fermion and scalar contributions separately and still

obtained a cancellation. However, there is an accidental symmetry here that obscures

the structure of the cancellations. For this reason, it is instructive to calculate as well

the one-loop quadratic divergent contributions to the A propagator. We will only

quote the results here, which you are invited to double-check (all the tricks needed

to do the calculation have been introduced in the calculation of the B propagator).

202

Supersymmetry Demystified

The one-loop quadratic divergent contributions to the propagator of A are, for

the tadpole diagrams,

A tadpole = 18ig

B tadpole = 6ig

Fermion tadpole =−24ig

Sum = 0 (9.77)

and for the non-tadpole diagrams, they are

A loop =−6ig

B loop =−2ig

Fermion loop = 8ig

Sum = 0 (9.78)

Again, there is one diagram that is only logarithmically divergent and therefore was

not included.

By looking at the results for the A propagator, it is now clear that the tadpole

diagrams cancel separately from the nontadpole contributions. These cancellations

are highly nontrivial. They obviously require a very subtle “conspiracy” between

all the parameters appearing in the lagrangian. Obviously, SUSY imposes very

stringent conditions on these parameters (not only at tree level, as we will discuss

in the next section). This is striking when we realize that there are three particles

and seven interaction terms but only one mass and one coupling constant in the

theory! Thus there are only two parameters, where we could have, in principle, 10

different parameters (three masses and seven coupling constants).

However, if we are only interested in having the quadratic divergences cancel, it

turns out that SUSY offers more constraints than what is necessary. For example,

consider leaving the dimensionless coupling constants in all the interactions the

same, as in SUSY, but let’s assign different symbols to the four different parameters

with a dimension of mass: the masses of the three particles m

, m

, and m



and

the dimensionful coupling constant that appears in the interaction L

I 2

, which we

will denote by m

The important point to notice is that the scalar masses m

and m

do not appear

at all in the quadratically divergent corrections to the propagator! On the other

hand, if we go over the calculation of the contribution from the fermion tadpole,

we can see that this diagram is actually proportional to m



, and therefore, for

the quadratic divergences to cancel, it is essential that m

= m



CHAPTER 9 Some Explicit Calculations

203

The conclusion is that we can change the masses of the scalar particles with-

out disrupting the cancellation of quadratic divergences! This would clearly break

SUSY because the fermion and the scalar would no longer be degenerate in mass,

but it would not spoil the cancellation of the quadratic divergences. Of course, we

have only shown this for the very speciﬁc case of the one-loop corrections to the B

propagator. But a more detailed analysis shows that it is in fact valid to all orders

of perturbation theory and for all processes!

In addition, we also may modify some of the coupling constants of the various

interactions without spoiling the cancellations of the quadratic divergences. Thus,

as long as we are motivated only by the desire to cancel these divergences, we

have actually more leeway with the parameters of the theory than SUSY allows.

We could therefore add terms to the lagrangian that would break explicitly the

invariance under SUSY but which would preserve the cancellation of quadratic

divergences in the theory. Such terms are said to break SUSY softly. We will list all

the possible terms that break SUSY softly in Chapter 14. They will play a crucial

role in Chapters 15 and 16 because they are required to break SUSY in the MSSM.

9.6 A Note on Nonrenormalization Theorems

Unfortunately, we don’t have enough space to explore more in-depth the perturba-

tive properties of supersymmetric theories. The very simple examples we did had

for their only goal to give you a peek at the types of cancellations of ultraviolet

divergences that occur owing to SUSY.

However, this very short chapter does not do justice to the power of SUSY. Given

more space, we would discover not only that all quadratic divergences cancel to

all orders of perturbation theory but also that the only renormalization required

in the Wess-Zumino model is a common wavefunction renormalization of all the

ﬁelds (which involves only a logarithmic divergence). The mass m and the coupling

constant g do not get renormalized at all to any order in perturbation theory!

The theorems demonstrating that certain parameters in supersymmetric theories

do not get renormalized at all are known as nonrenormalization theorems. A proof

using a diagrammatic approach was worked out in Ref. 22. Seiberg

has derived

the same result using a very nifty trick that makes the proof extremely simple. The

basic idea is that the parameters of the theory, such as m and g in the Wess-Zumino

model, are treated as the expectation values of some new ﬁelds. Of course, these are

not physical ﬁelds but rather simply mathematical tricks to carry out the proof and

therefore are sometimes referred to as spurious ﬁelds or spurions. The introduction

of these spurious ﬁelds enhances the symmetry of the lagrangian, introducing an

additional U(1) symmetry. Using the superspace approach that we will cover in

later chapters and the holomorphicity of the potential, it is a simple matter to prove

204

Supersymmetry Demystified

that some interactions cannot get renormalized to any order in perturbation theory.

A simple illustration of this technique can be found in Section 3 of Ref. 43, and

more details are given in Section 8.2 of Ref. 8.

Let us also add that calculations of Feynman diagrams in SUSY are simpliﬁed

greatly by the use of so-called supergraphs. These graphs involve the propaga-

tors (or superpropagators) of the superﬁelds that we will introduce in Chapter 11.

The end result is that the effect of all the ﬁeld members of a supermultiplet are

taken into account simultaneously instead of having many diagrams with the var-

ious ﬁelds. This obviously simpliﬁes the calculations greatly, and is a powerful

tool to build directly into the Feynman diagrams the highly nontrivial relations be-

tween the various terms imposed by SUSY. The supergraph approach therefore not

only simpliﬁes calculations but also facilitates the proof of many results, including

nonrenormalization theorems. This is unfortunately beyond the scope of this book,

but if you are interested, you can ﬁnd a nice introduction in Ref. 47 and a more

technical presentation in Ref. 49.

9.7 Quiz

1. What is the difference between the propagator of a Dirac fermion and the

propagator of a Majorana fermion?

2. How many different parameters are there in the Wess-Zumino model (for a

single multiplet)?

3. Are supersymmetric theories completely free of all divergences?

4. Give one example of a term we could add to the lagrangian that would break

SUSY but which would not spoil the cancellation of quadratic divergences.

5. What is meant by saying that an interaction breaks SUSY softly?

CHAPTER 10

Supersymmetric

Gauge Theories

The only theory we have built so far contained a spinor and a scalar ﬁeld. If we are

to apply supersymmetry (SUSY) to real life, we need to deal with gauge theories.

As we saw in Section 7.4, a vector (massless) supermultiplet contains states with

helicities h = 1/2 and h = 1. Together with the corresponding CPT conjugates,

we therefore have four states with h =±1/2, ±1. The particle content is therefore

a massless fermion and a massless spin 1 particle. If we consider an abelian U (1)

gauge theory, this is all the particle content we need to construct the supersymmetric

version because there is only one gauge ﬁeld. For nonabelian gauge theories, we

will, of course, need to introduce as many fermions as there are gauge ﬁelds, and

these fermions will have to transform in the same representation as the gauge ﬁelds.

But let’s not get ahead of ourselves, and let’s start by building a supersymmetric

abelian gauge theory. By the way, the term gauge multiplet is often used to denote

a vector multiplet, and we will use both terms interchangeably.