Labelle P. Supersymmetry DeMYSTiFied

Подождите немного. Документ загружается.

226

Supersymmetry Demystified

Note that because of the covariant derivative, F and χ (and their hermitian

conjugates) pick up an extra term compared with what we had previously, when

the chiral multiplet had no charge. To be explicit, these are

δF = previous terms + qζ

†

¯σ

χ A

δF

†

= previous terms + qχ

†

¯σ

ζ A

δχ = previous terms + qφ A

iσ

∗

δχ

†

= previous terms − qφ

†

iσ

These will generate new terms in the variation of the terms in the free part of

the lagrangian for the chiral multiplet contained in Eq. (10.36) that we did not have

before. Let us use (δF )

to represent the new term appearing in the variation of F

and similar expressions for the other ﬁelds, with a subscript A to remind us that

this new term contains the gauge ﬁeld A

. Then the new terms generated in the

variation of the free part of the chiral multiplet lagrangian are simply

δ(L

free

) = i



δχ

†

)

¯σ

∂

χ +iχ

†

¯σ

∂

(δχ )

+ (δ F

†

)

F + F

†

(F)

(10.41)

Now consider the variation of the terms in the ﬁrst interaction lagrangian,

Eq. (10.37), under SUSY:

δ(L

int

)

= iq(δφ) A

∂

†

+iqφ(δA

)∂

†

+iqφ A

∂

(δφ

†

)

−iq(δφ

†

∂

φ −iqφ

†

(δ A

)∂

φ −iqφ

†

∂

(δφ)

−q(δχ

†

¯σ

χ −q(δ A

)χ

†

¯σ

χ −qχ

†

¯σ

(δχ ) (10.42)

The variation of Eq. (10.40) is

δ(L

int

)

= c

(δφ

†

)χ ·λ + c

†

(δχ ) · λ + c

†

χ ·(δλ)

(δφ)

λ · ¯χ +c

φ(δ

λ) · ¯χ +c

λ · δ ¯χ

(δφ

†

)φ D + c

†

(δφ)D +c

†

φδD (10.43)

The goal is to see if there is a choice of values for c

, c

, and a such that the

sum of Eqs. (10.41), (10.42), and (10.43) cancel, modulo total derivatives. This

is obviously a huge undertaking! We will not carry out the full calculation here

but simply consider just enough terms to allow us to determine the values of these

three constants. We also will ﬁnd that one of the SUSY transformations must be

modiﬁed.

CHAPTER 10 Supersymmetric Gauge Theories

227

Terms Linear in D

Let’s focus on the terms linear in D that must cancel among themselves (modulo

total derivatives, as usual). There are four such terms: the two terms that have

explicit factors of D and the two terms generated by the variation of λ and its

hermitian conjugate. These are

a(φ

†

Dχ · ζ + φ D

ζ · ¯χ)+c

(φ D ¯χ ·

ζ + φ

†

Dζ · χ)

Of course, the terms in φ and the terms in φ

†

must cancel out separately. We see

that the condition in both cases is

a +c

= 0 (10.44)

Terms with Four Spinors

Next, consider terms that are generated with four spinors. One source is from the

next to last term in Eq. (10.42). The other two sources are from the ﬁrst and fourth

terms of Eq. (10.43). We get

−qaχ

†

¯σ

χ(ζ

†

¯σ

λ + λ

†

¯σ

ζ)+ c

¯χ ·

ζχ · λ + c

ζ · χ

λ · ¯χ (10.45)

Using the identity (A.57), we have



†

¯σ



(ζ

†

¯σ

β) = 2( ¯χ ·

ζ )(χ · β)

so Eq. (10.45) becomes

−2qa( ¯χ ·

ζ )(χ · λ) − 2qa( ¯χ ·

λ)(χ ·ζ)+ c

( ¯χ ·

ζ )(χ · λ) + c

(ζ · χ)(

λ · ¯χ)

= (c

− 2qa)



( ¯χ ·

ζ )(χ · λ) + (ζ · χ)(

λ · ¯χ)



where the parentheses around the spinor dot products have been included just to

make the expression easier to read. We have used the fact that the order in spinor

dot products does not matter; e.g.,

λ · ¯χ = ¯χ ·

λ.

We therefore get the condition

− 2qa = 0 (10.46)

228

Supersymmetry Demystified

Putting together Eqs. (10.44) and (10.46), we see that we can express both c

and c

in terms of a, i.e.,

= 2qa c

=−2qa

(10.47)

Terms with φ and a Derivative of φ

We have contributions of this form in the second and ﬁfth terms of Eq. (10.42). We

also generate terms like this from the variation of χ and χ

†

in the second and sixth

terms of Eq. (10.43). Explicitly, these are [using the explicit form for the spinor dot

products, Eq. (A.37)]

iqa



φ∂

†

− φ

†

∂



†

¯σ

λ + λ

†

¯σ



+ c

†

(−i∂

φ)



iσ

∗



(−iσ

)λ

−c

φλ

†

(iσ

)



i∂

†

iσ



(10.48)

At ﬁrst sight, it seems as if there are no other terms of this form. But we have

to remember that terms related by integration by parts must be considered as being

equivalent. Thus we also must include terms of the form φφ

†

times the derivative

of other ﬁelds. There is indeed such a term: the last term of Eq. (10.43):

†

φδD =−2iqa

†



(∂

†

) ¯σ

ζ − ζ

†

¯σ

∂



=−2iqa

†

φ∂



†

¯σ

ζ − ζ

†

¯σ



(10.49)

where we have used c

=−2qa

We must ﬁnd if it’s possible to get the terms in Eqs. (10.48) and (10.49) to

cancel, modulo total derivatives. Adding the two terms and taking the transpose of

the pieces in the last two terms of Eq. (10.48), we get

iqa



φ∂

†

− φ

†

∂



†

¯σ

λ + λ

†

¯σ



−ic

†

(∂

φ)ζ

†

iσ

μT

iσ

+ic

φ(∂

†

)λ

†

iσ

μT

iσ

ζ − 2iqa

†

φ∂



†

¯σ

ζ − ζ

†

¯σ



Using the identity (A.5) to simplify the two terms with σ

matrices, and setting

= 2qa, we get a much simpler expression:

iqa



φ∂

†

+ φ

†

∂



†

¯σ

λ − λ

†

¯σ



− 2iqa

†

φ∂



†

¯σ

ζ − ζ

†

¯σ



(10.50)

CHAPTER 10 Supersymmetric Gauge Theories

229

There is no value of a for which this is zero (other than the trivial and uninteresting

a = 0). However, it is not necessary for these terms to cancel out identically, all

we need is for them to be equal to zero modulo total derivatives! Thus, if there is

a value of a for which the whole thing is a total derivative, we have achieved our

goal. Note that the ﬁrst parentheses may be written as

(φ∂

†

+ φ

†

∂

φ) = ∂

(φ

†

φ)

and then it becomes obvious that Eq. (10.50) is a total derivative at the condition

that iqa = 2iqa

. This ﬁnally gives us

1 − 2a

= 0 ⇒ a =−

√

where the choice of sign is purely conventional. Using this in Eq. (10.47), we ﬁnally

get

=−

√

2qc

=−q

We have now ﬁxed completely the only three parameters available to us. But there

are still many many more terms to cancel out! It turns out that, quite remarkably,

almost all terms do cancel out with the values of a, c

, and c

we have determined.

We won’t carry out the entire calculation here, for lack of space (and of energy),

but we will point out the single set of terms that do not cancel out and show how

the problem is taken care of.

Terms in F

The problem appears in the terms linear in F or F

†

. Some of these terms are

generated by the variation of χ and χ

†

in the seventh and last terms of Eq. (10.42)

and in the second and sixth terms of Eq. (10.43):

−qF

†

¯σ

χ −qFχ

†

¯σ

ζ −

√

2qφ

†

Fζ · λ −

√

2qF

†

λ ·

ζ (10.51)

230

Supersymmetry Demystified

In addition, we have the two terms produced by the variation of F

†

F in Eq.

(10.41):

(δF

†

)

F + F

†

(δF)

= qA

†

¯σ

χ +qA

Fχ

†

¯σ

We see that these terms cancel out the ﬁrst two terms of Eq. (10.51). However,

we are left with the last two terms of Eq. (10.51), which cannot be canceled with

anything. The only way out is to introduce an extra term in the variation of F.We

must impose

δF =−iζ

†

¯σ

χ +

√

2qφ

λ ·

where the ﬁrst term is what we had previously. Of course, we also have

δF

†

= i(D

χ)

†

¯σ

ζ +

√

2qφ

†

λ · ζ

With this modiﬁcation and with our choices of c

, c

, and a, all the terms in

Eqs. (10.41), (10.42), and (10.43) cancel out. Amazing!

Final Result for the Coupling of a Chiral with an

Abelian Gauge Multiplet

The full lagrangian that couples a chiral multiplet with an abelian multiplet is

therefore

L = (D

φ)

†

φ) + iχ

†

¯σ

χ + F

†

F −

μν

+i λ

†

¯σ

∂

+ ξ D −

√

2q(φ

†

χ ·λ + h.c.) −qφ

†

φ D

Note the interesting fact that the coupling constants in the interactions terms are

all proportional to the electric charge, a relation imposed by SUSY. In non-SUSY

theories, there would be no way to generate this type of constraint other than putting

it in by hand.

CHAPTER 10 Supersymmetric Gauge Theories

231

The ﬁelds transform as

δ A

=−

√

(ζ

†

¯σ

λ + λ

†

¯σ

ζ)

δλ =−

√

μν

¯σ

ζ −

√

Dζ

δ D =

√

†

¯σ

∂

λ −

√

(∂

†

) ¯σ

δφ = ζ · χ

δχ =−i(D

φ)σ

iσ

∗

+ Fζ

δF =−iζ

†

¯σ

χ +

√

2qφ

λ ·

ζ (10.52)

The lagrangian (10.54) does not contain any interaction among the ﬁelds of the

chiral multiplet. We have seen in Section 8.1 [see Eq. (8.26)] that the interaction

lagrangian of a single chiral multiplet, which is written entirely in terms of the

superpotential W,isgivenby

∂W

∂φ

F −

∂

∂φ

χ ·χ + h.c.

But since all the members of the chiral multiplet have the same charge, there is

no superpotential W for which this expression is gauge-invariant (recall that the

superpotential depends only on φ, not on its hermitian conjugate). Therefore, we

must set W equal to zero to respect gauge invariance.

If we allow for the presence of several chiral multiplets, as in Section 8.2, then it

becomes possible to write down gauge-invariant interactions between them at the

condition that there are some combinations of the charges that add up to zero. The

interaction lagrangian can be read off from Eq. (8.60):



∂W

∂φ

−

∂

∂φ

· χ

+ h.c.



(10.53)

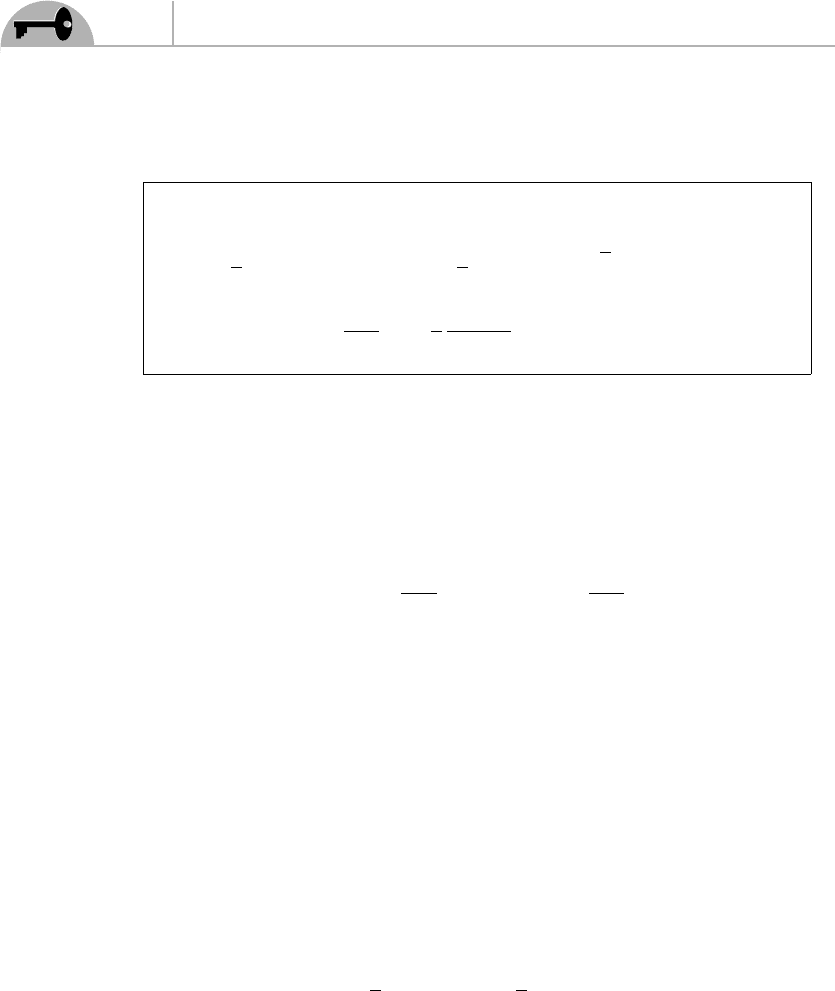
232

Supersymmetry Demystified

If we include this term and allow for the presence of several left-chiral multiplets,

we obtain the following generalization:

L =(D

)

†





+i χ

†

¯σ

+ F

†

−

μν

+i λ

†

¯σ

∂

λ +

+ ξ D −

√

2q ×



†

· λ + h.c.



−qφ

†

D +



∂W

∂φ

−

∂

∂φ

· χ

+ h.c.



(10.54)

10.7 Eliminating the Auxiliary Fields

Eliminating the auxiliary ﬁelds F

leads to the replacement

†



∂W

∂φ

+ h.c.



=−



∂W

∂φ



Now let’s turn our attention to the auxiliary ﬁeld D. Can we also eliminate it

for a general supersymmetric abelian gauge theory? The answer is yes, and it is

actually easier than eliminating the auxiliary ﬁelds F

. The solution to the equation

of motion δL/δ D = 0is

D = q

†

− ξ

where the ξ comes from the Fayet-Illiopoulos term. Plugging this back into the D

dependent terms in the lagrangian, we get

−q

†

D +

+ ξ D =−





†

− ξ



(10.55)

where we wrote the summation symbol in the ﬁrst term to make it clear that the

sum is performed before squaring the expression.

We see that this represents another contribution to the potential of the scalar

ﬁelds. After elimination of the auxiliary ﬁelds using their equations of motion, the

CHAPTER 10 Supersymmetric Gauge Theories

233

total lagrangian therefore can be written as

L = L

=D=0

−



∂W

∂φ



−





†

− ξ



(10.56)

This means that the scalar ﬁeld potential is simply

V (φ

) =



∂W

∂φ







†

− ξ



(10.57)

To be precise, these terms not only contain the interactions of the scalar ﬁelds, but

they also contain their masses as well.

Equation (10.57) will play a crucial role in our discussion of SUSY spontaneous

symmetry breaking in Chapter 14.

10.8 Combining a Nonabelian Gauge

Multiplet With a Chiral Multiplet

As in the abelian case, we assign the ﬁelds of the chiral multiplet (φ, χ, and F)

to some representation of the gauge group, the usually choice being the funda-

mental or antifundamental representations. These representations of SU(N ) are

N -dimensional, so we must take N copies of each of the ﬁelds of the chiral mul-

tiplet. We then replace the derivatives acting on the these ﬁelds with covariant

derivatives. For example, if we assemble N scalar ﬁelds transforming in the funda-

mental representation φ

into a column vector φ,wehave

φ = ∂

φ +igA

As we saw in Section 10.5, this is a shorthand for

= ∂

+ig A





We have, of course, a similar expression for the covariant derivative acting on the

chiral spinors ﬁelds χ

If we do not consider self-interactions of the chiral multiplet (i.e., if we set

the superpotential equal to zero), the simplest lagrangian containing interactions

234

Supersymmetry Demystified

between a chiral and nonabelian gauge multiplets is

L =





†

) +i(χ

)

†

¯σ

+ (F

)

†

−

μν

+i (λ

)

†

¯σ

λ)

≡ (D

φ)

†

φ) + iχ

†

¯σ

χ + F

†

F −



μν



+i λ

†

¯σ

λ +

where the index b runs from 1 to N , whereas the index a runs from 1 to N

− 1.

This is the nonabelian generalization of Eq. (10.36). As mentioned earlier, there

is no Fayet-Illiopoulos term in the nonabelian case because such a term is not

gauge-invariant.

This lagrangian contains interactions between the gauge ﬁelds of the gauge

multiplet and the ﬁelds χ and φ through the covariant derivatives, but we also can

add extra gauge-invariant interactions between the ﬁelds of the two multiplets, as

we did in the abelian case.

The ﬁelds of the vector multiplet are all in the adjoint representation, so what

we need is to build gauge-invariant expressions out of ﬁelds transforming in the

fundamental and the adjoint representations. From Section 10.3, we know that the

transformation of a ﬁeld belonging to the adjoint representation, e.g., F

μν

,isgiven

by [see Eqs. (10.22) and (10.23)]

μν

→ UF

μν

†

where F

μν

= F

μν

. The other ﬁelds of the vector multiplet, ﬁelds λ and D, trans-

form the same way. On the other hand, the ﬁelds of the chiral multiplet transform

in the fundamental representation, i.e.,

φ → U φ

and similarly for χ and F. Here, it is understood that φ actually stands for a col-

umn vector with N entries φ

. We therefore have the following 27 gauge-invariant

combinations available:

(φ, χ, F)

†

μν

,λ,D)(φ, χ , F)

Nine terms are real, whereas the remaining 18 terms form 9 pairs related by her-

mitian conjugation.

However, the dimension of most of these terms is too large. Recall that the ﬁelds

of the gauge muliplet F

μν

, D

, and λ

have dimensions 2, 2, and 3/2, respectively,

CHAPTER 10 Supersymmetric Gauge Theories

235

whereas the ﬁelds F

, φ

, and χ

have dimensions 2, 1, and 3/2. If we don’t worry

about Lorentz invariance for now, the available gauge-invariant terms of dimension

4 or less are

†

μν

φφ

†

Dφφ

†

λχ +h.c. φ

†

λφ +h.c. (10.58)

These are the obvious nonabelian generalization of Eq. (10.38), and the exact

same arguments that we used after that equation show once more that the only

Lorentz invariants of dimension 3 or less are

int

= c

†

λ · χ +c

λ · ¯χ +c

†

Dφ

where c

must be real, and we have taken c

to be real as well. Without showing all

the matrix indices, it may be a bit clearer to show explicitly the matrix structure of

this expression by writing

int

= c



†



· λ

+ c



φT

¯χ



+ c



†



This is, of course, the nonabelian generalization of Eq. (10.40). If we do show all

the gauge indices, we have

int

= c



(φ

)

†







· λ

+ c



(φ)





¯χ



+ c



(φ

)

†







Now we should repeat the steps of Section 10.6 to ﬁnd out if there is a choice of c

and c

for which the theory is supersymmetric. We won’t present the calculation

here because it is almost identical to what we did in Section 10.6. The ﬁnal result

turns out to be that the theory is SUSY invariant at the same condition that we found

for the abelian case, namely,

=−

√

2g and c

=−g

The complete lagrangian of a chiral multiplet interacting with a nonabelian gauge

multiplet is ﬁnally

L =(D

φ)

†

φ) + i(χ )

†

¯σ

χ +(F)

†

F −



μν



+i (λ)

†

¯σ

−

√

2gφ

†

λ · χ −

√

2gφ

λ · ¯χ − gφ

†

Dφ

(10.59)