Кузюрин Н.Н. Фомин С.А. Сложность комбинаторных алгоритмов. Курс лекций

Подождите немного. Документ загружается.

Алгоритм 24 Динамическое программирование для задачи 0-1 РЮКЗАК

def knapsack_dylp (A, B, C):

print , A, , B, , C

T ← {0: 0} # Хэш: самая большая стоимость набора для веса - вес:стоимость

← {0: [ ]}

Цикл по всем предметам

for i ∈ xrange (len (A)) :

print C[i], , A[i], ,

← dict (T ) # Копируем T

k−1

в T

old

print T

Цикл по всем полученным частичным суммам

for x ∈ :

if (x + A[i]) ≤ B :

if ¬(x + A[i] ∈ T ) ∨ (T [x + A[i]] < [x] + C[i]):

T [x + A[i]] ← [x] + C[i]

[x + A[i]] ← [x] + [i]

print , T

← max (T.values ())

← [argmax (T )]

print , ,

return ( , )

2. размер множества отобранных частичных решений не превосходит B;

Упражнение 46 Постройте алгоритм динамического программирования для задачи 21 «Knapsack», осно-

ванный на отборе наиболее «легких» частичных решений. Какова будет его временная сложность?

Таким образом, для небольших значений параметров c

, . . . , c

, или B, можно построить эффективный псевдополи-

номиальный алгоритм для точного решения задачи о рюкзаке. Еще раз отметим, что он не является полиномиальным.

При росте значений параметров c

, . . . , c

, B эффективность этого алгоритма будет уменьшаться. Кроме этого, стоит

помнить и о пространственной сложности алгоритма — нам требуется Ω(B) или Ω(f

∗

) памяти для хранения частичных

решений.

Упражнение 47 Придумайте входные наборы для алгоритма 24 «Рюкзак-ДинПрог» на которых он будет

работать экспоненциальное время.

Упражнение 48 Придумайте входные наборы для алгоритма из упражнения 46 на которых он будет рабо-

тать экспоненциальное время.

Что же делать, если параметры c

, . . . , c

или B задачи велики настолько, что сложность алгоритма 24 «Рюкзак-

ДинПрог» (или алгоритма из упражнения 46) не укладывается в требования технического задания по времени или по

памяти?

Во-первых, можно организовать «разумный» перебор, не привязываясь к таблице, ограниченной малостью вход-

ных параметров типа B, устроив перебор, по так называемым доминирующим частичным решениям.

Определение 52 Одно подмножество предметов для задачи 21 «Knapsack» доминирует другое такое под-

множество, если стоимость первого набора предметов больше, а вес — меньше или равен весу второго на-

бора.

Т.е. набор доминирующих подмножеств есть набор Парето-оптимальных решений, т.е. таких решений, в которых

нельзя улучшить один параметр (стоимость), без ухудшения другого параметра (увеличения веса).

Алгоритм Немхаузера-Ульмана (алгоритм 25 «Рюкзак Немхаузера-Ульмана»), аналогично алгоритму 24 «Рюкзак-

ДинПрог», порождает подмножества поочередным добавлением предметов, только вместо таблицы (размера не более

B) «наиболее дорогих решений», поддерживается список доминирующих решений, упорядоченных по возрастанию

веса. При добавлении каждого предмета порождается новый список (в котором подмножества также упорядочены по

весу и являются доминирующими по отношению к друг другу). Остается слить эти два списка, удалив доминируемые

подмножества.

Заметим, что и алгоритм 25 «Рюкзак Немхаузера-Ульмана», остается в наихудшем случае экспоненциальным.

Упражнение 49 Придумайте входные наборы для алгоритма 25 «Рюкзак Немхаузера-Ульмана» на которых

он будет работать экспоненциальное время.

Но практика использования показала, что на реальных данных алгоритм 25 «Рюкзак Немхаузера-Ульмана» рабо-

тает достаточно хорошо. Объяснение этому будет дано в разделе 3.1.3.

Если же необходимо застраховаться от возможных «плохих» входных данных, то можно использовать идею ал-

горитма 24 «Рюкзак-ДинПрог» для эффективного приближенного решения задачи 21 «Knapsack» с любой наперед

заданной точностью (см раздел. 2.2.2).

2.2.2 Полностью полиномиальная приближенная схема для задачи о рюкзаке

Одним из общих подходов к решению переборных задач является разработка приближенных алгоритмов с гарантиро-

ванными оценками качества получаемого решения

. Особую роль среди приближенных алгоритмов играют те, которые

способны находить решения с любой фиксированной наперед заданной точностью (см. определение 35).

Определение 53 Алгоритм с мультипликативной точностью (1 + ε) называется ε-оптимальным.

Тот же термин ε-оптимальное используется для обозначения допустимого решения со значением целевой функ-

ции, отличающемся от оптимума не более, чем в (1 + ε) раз (таким образом, задача, стоящая перед ε-оптимальным

алгоритмом состоит в отыскании какого-либо ε-оптимального решения).

Алгоритм, не гарантирующий точность решения, однако применяемый на практике из-за хороших практических результатов принято называть

эвристикой

Алгоритм 25 Алгоритм Немхаузера-Ульмана для задачи о рюкзаке

def mergeSolutions ( , ) : # Слияние списков доминирующих решений с удалением доминируемых

i ← j ← 0 # можем считать, что входные списки непусты.

← [ ]

while (i < len ( ) ∨ j < len ( )):

while (i < len ( ) ∧ j < len ( ) ∧ ( [i]. ≥ [j]. ) ∧ ( [i]. ≤ [j]. )):

j ← j + 1

while (i < len ( ) ∧ j < len ( ) ∧ ( [i]. ≤ [j]. ) ∧ ( [i]. ≥ [j]. )):

i ← i + 1

if i < len ( ) ∧ j < len ( ):

if ( [i]. < [j]. ):

.append ( [i])

i ← i + 1

else:

.append ( [j])

j ← j + 1

elif i < len ( ):

.append ( [i])

i ← i + 1

else: # т.е. j<len(list2)

.append ( [j])

j ← j + 1

return

Алгоритм Немхаузера-Ульмана (Nemhauser-Ullman)

def knapsack_nemhauser_ullman ( , B) :

print , B, ,

← [Solution ()]

for ∈ :

print ,

← [ ]

for ∈ :

if . + . ≤ B :

.append ( + )

print , , ,

← mergeSolutions ( , )

print ,

return [len ( ) − 1]

Определение 54 Полностью полиномиальной аппроксимационной схемой называется приближенный алго-

ритм, в котором уровень точности ε выступает в качестве нового параметра, и алгоритм находит ε-оптимальное

решение за время, ограниченное полиномом от длины входа и величины ε

−1

Только одно обстоятельство является препятствием для построения полностью полиномиальной аппроксимацион-

ной схемы для задачи 0-1 РЮКЗАК методом динамического программирования. Это наличие «больших» коэффици-

ентов в целевой функции.

Действительно, как мы видели выше, динамическое программирование дает точный псевдополиномиальный алго-

ритм для задачи о рюкзаке со сложностью O(nf

∗

) или O(nB). Если величины f

∗

и B не ограничена сверху никаким

полиномом (то есть имеются большие коэффициенты), то этот псевдополиномиальный алгоритм не является полино-

миальным.

Однако, к счастью, существует общий метод (который условно можно назвать масштабированием), позволяю-

щий перейти к задаче с небольшими коэффициентами в целевой функции, оптимум которой не сильно отличается от

оптимума исходной задачи.

Зададимся вопросом: что произойдет, если мы отмасштабируем коэффициенты c

, . . . , c

, поделив их нацело (с

остатком) на некоторый параметр scale, решив «отмасштабированную» задачу, и затем снова умножив коэффициенты

на параметр scale? Каково будет изменение значения целевой функции после этой операции?

Более формально, положим c

= bc

/scalec, ˜c

= c

· scale и обозначим оптимум «отмасштабированной» задачи (с

) через f

, а оптимум задачи с коэффициентами ˜c

через

Ясно, что любое допустимое решение «отмасштабированной» задачи является также допустимым решением ис-

ходной задачи. Кроме того, абсолютная погрешность не превосходит величины n · scale. Если потребовать, чтобы эта

величина не превосходила

1+ε

∗

, то по определению получим, что каждое допустимое решение исходной задачи отли-

чается от решения «отмасштабированной» задачи не более, чем на эту же величину.

Обозначая оптимум «отмасштабированной» задачи через

f, получаем, что

f ≥ f

∗

−

1 + ε

∗

(1 + ε)

т.е. оптимум «отмасштабированной» задачи отличается от оптимума исходной задачи не более, чем в 1 + ε раз.

При этом величина значение оптимального решения для «отмасштабированной» задачи уменьшается не менее, чем

в scale раз по сравнению с исходной. И таким образом, для отмасштабированной задачи, версия алгоритма 24 «Рюк-

зак-ДинПрог», ориентированная на отбор «самых легких решений» будет работать существенно меньшее время.

Однако проблема состоит в том, что в момент масштабирования мы не знаем величины оптимума f

∗

, и не можем

выбрать коэффициент scale, который, чтобы решение было ε-оптимальным, не должен превышать

εf

∗

n(1+ε)

, с одной

стороны, с другой — желательно максимально приблизить его к этой оценке, чтобы уменьшить коэффициенты в задаче.

Поэтому, важное наблюдение состоит в том, что вместо f

∗

можно рассматривать нижнюю оценку f

∗

, и, обозначив

ее f

, выбирать параметр масштабирования

scale = max{1, b

εf

n(1 + ε)

c}.

Тогда все вышеизложенные соображения о точности «отмасштабированного» решения сохранят силу. Таким образом,

стоит задача выбора нижней оценки f

, которую можно найти быстро с одной стороны, и желательно чтобы она была

как можно ближе к f

∗

, т.к. это даст возможность увеличить коэффициент scale, и тем самым, сильнее уменьшить

коэффициенты c

, . . . , c

и время выполнения алгоритма. Таким образом, общая схема алгоритма, представлена как

процедура «knapsack_ptas_generic», в алгоритме 26 «Рюкзак-PTAS-общая схема», которой на вход, кроме обычных

параметров рюкзака, передают функцию «f_lower_bound», используемую для получения нижней оценки стоимости

решения.

Осталось найти такую функцию. Например, можно рассмотреть тривиальную аппроксимацию

max

≥ f

∗

≥ f

≡ c

max

где c

max

= max

Получим функцию «knapsack_ptas_trivial» в алгоритме 27 «Рюкзак-PTAS».

Сложность этого алгоритма — O(nf

) (см. анализ алгоритма 24 «Рюкзак-ДинПрог»).

Учитывая, что f

∗

≤ nc

max

, а

f ≤ nb

max

scale

c, получаем оценку сложности алгоритма «knapsack_ptas_trivial»:

O(n

f) = O



max

scale



= O



(1 + ε)



= O





Можно ли улучшить эту оценку? Ответ на этот вопрос положителен. Для этого рассмотрим менее наивную ап-

проксимацию величины f

∗

. Вспомним алгоритм 19 «Рюкзак-Жадный» из раздела 2.1.3. Для значения решения f

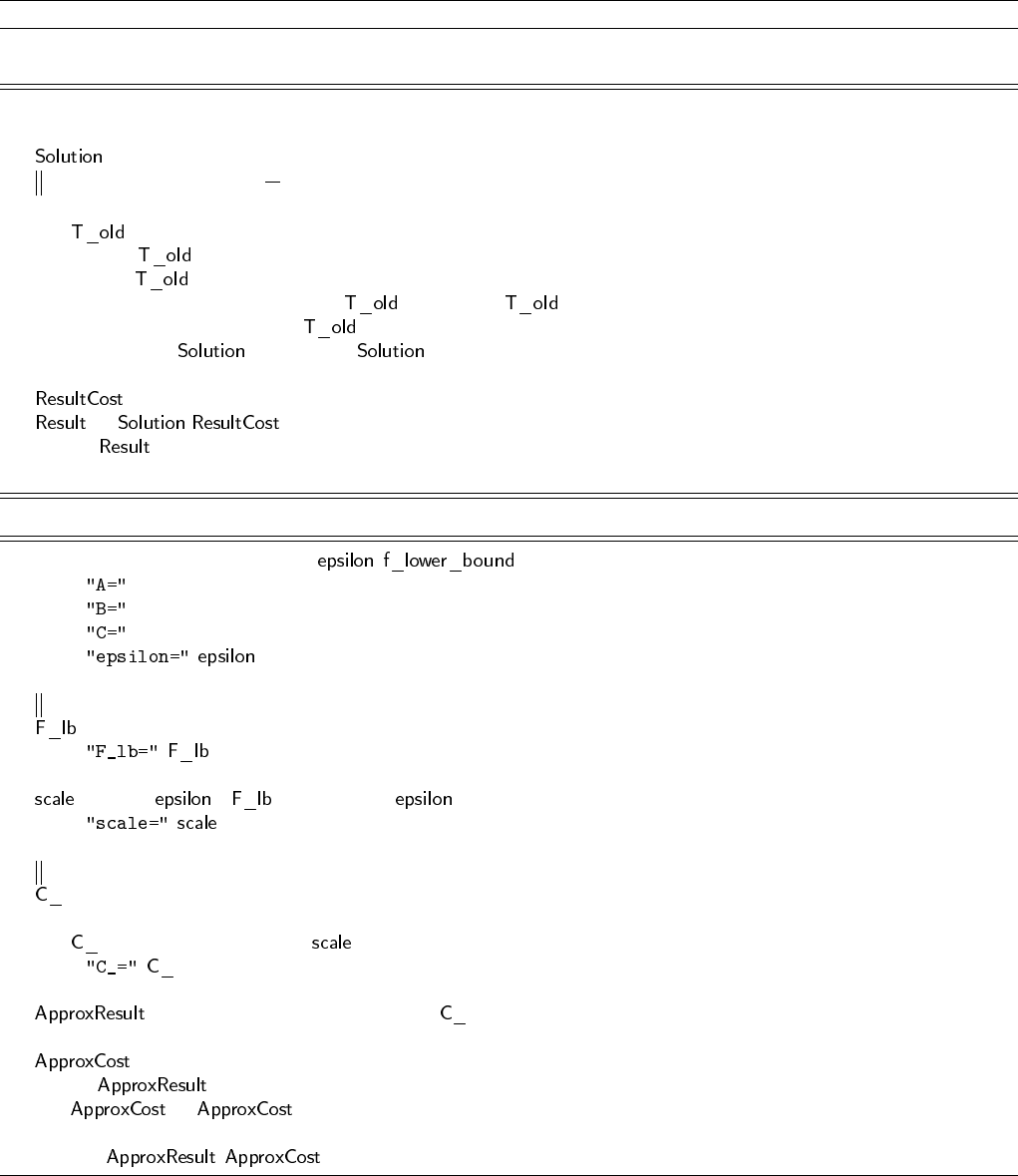
Алгоритм 26 PTAS для задачи 0-1 РЮКЗАК: Общая схема

Динамическое программирования для рюкзака, с отбором "наиболее легких"частичных решений.

def knapsack_dylp_lightest (A, B, C) :

T ← {0: 0} # Хэш: самый малый вес для стоимости - стоимость:минимальный вес

← {0: [ ]}

Цикл по всем предметам

for i ∈ xrange (len (A)) :

← dict (T ) # Копируем T

k−1

в T

old

for x ∈ :

if ( [x] + A[i]) ≤ B :

if (¬(x + C[i] ∈ T )) ∨ ( [x] + A[i] < [x + C[i]]):

T [x + C[i]] ← [x] + A[i]

[x + C[i]] ← [x] + [i]

← max (T.keys ())

← [ ]

return

PTAS для рюкзака. Общая схема.

def knapsack_ptas_generic (A, B, C, , ):

print , A

print , B

print , C

print ,

Вычисляем нижнюю оценку стоимости и параметр округления scale

← f_lower_bound (A, B, C)

print ,

← ﬂoor ( ∗ /len (C)/(1 + ))

print ,

Округляем коэффициенты

← [ ]

for i ∈ xrange (len (A)) :

.insert (i, int (ﬂoor (C[i]/ )))

print ,

← knapsack_dylp_lightest (A, B, )

← 0

for i ∈ :

← + C[i]

return ( , )

Алгоритм 27 PTAS для задачи 0-1 РЮКЗАК: Алгоритмы сложности

def knapsack_lower_bound_trivial (A, B, C):

Простая оценка нижней границы стоимости решения.

return max (C)

def knapsack_lower_bound_greedy (A, B, C):

Оценка нижней границы через жадный алгоритм.

return knapsack_greedy (A, B, C)

PTAS для рюкзака, сложности O(

)

def knapsack_ptas_trivial (A, B, C, ) :

return knapsack_ptas_generic (A, B, C, , )

PTAS для рюкзака, сложности O(

)

def knapsack_ptas_nontrivial (A, B, C, ) :

return knapsack_ptas_generic (A, B, C, , )

полученного модифицированным жадным алгоритмом для задачи о рюкзаке, и оптимального значения f

∗

выполняется

∗

≤ f

∗

. (2.6)

Используя эту оценку, получаем функцию «knapsack_ptas_nontrivial» в алгоритме 27 «Рюкзак-PTAS». Аналогич-

но, учитывая, что f

∗

≤ 2f

, а

f ≤

∗

scale

≤

scale

получаем оценку сложности для этого алгоритма:

O(n

f) = O



scale



= O



(1 + ε)



= O





Глава 3

Вероятностные алгоритмы и

вероятностный анализ.

3.1 Вероятностный анализ детерминированных алгоритмов

3.1.1 Задача упаковки. Анализ сложности в среднем.

Среди подходов к решению NP-трудных задач можно выделить два. Первый заключается в построении приближен-

ных алгоритмов с гарантированными оценками точности получаемого решения (См. раздел 2), а второй — в отказе от

анализа сложности алгоритмов по наихудшему случаю и переходе к анализу сложности в среднем. Настоящая лекция

посвящена изучению второго подхода (анализу сложности в среднем).

Известно, что большинство задач дискретной оптимизации являются NP-трудными и для них существование по-

линомиальных алгоритмов маловероятно. Несмотря на это для многих исходных данных (входов) такие задачи бывают

легко разрешимы на практике. Таким образом, вся трудность задачи может заключаться в небольшом подмножестве

входов. Проблема нахождения таких входов важна для экспериментальной оценки эффективности алгоритмов, и, в то

же время, играет заметную роль в математической криптографии. Концепция сложности в среднем для таких задач

представляется более адекватной, чем концепция сложности в худшем случае.

Имеется еще одно соображение в пользу перехода от анализа по худшему случаю к анализу сложности в среднем.

Оно состоит в том, что некоторые практически эффективные алгоритмы не являются эффективными при анализе по

худшему случаю. Пожалуй наиболее известным примером такого алгоритма является симплекс-метод решения задач

линейного программирования, который не являясь полиномиальным алгоритмом, поразительно хорошо зарекомендо-

вал себя при решении практических задач.

Таким образом, естественные попытки ослабить требования в определении эффективности привели к понятию слож-

ности в среднем (average case complexity), под которым, грубо говоря, понимается математическое ожидание времени

работы алгоритма при заданном вероятностном распределении на исходных данных. С середины 80-х годов начала

развиваться теория сложности в среднем, в некотором смысле аналогичная теории полиномиальной сводимости для

NP-трудных задач. Кроме того, для ряда NP-полных задач удалось построить полиномиальные в среднем алгорит-

мы. Однако, успехи достигнутые здесь оказались гораздо скромнее результатов в теории сложности при анализе по

худшему случаю.

В последнее время получен ряд интересных результатов для задач типа рюкзака с константным числом ограни-

чений, введено новое понятие «сглаженной сложности» (smoothed complexity)и доказано, что некоторые варианты

симплекс-метода имеют полиномиальную сглаженную сложность, построены приближенные полиномиальные в сред-

нем алгоритмы нахождения максимальной клики в графе, с гарантируемыми оценками точности существенно лучшими

аналогичных оценок для худшего случая.

Перейдем к конкретизации сказанного выше. Пусть для данного алгоритма A время его работы на входе I обозна-

чается через T

(I). Пусть также для каждого натурального n задано распределение вероятностей на входах I длины

n, обозначаемое P

(I). Поскольку T является случайной величиной, естественным кажется определить среднее время

работы алгоритма A как математическое ожидание времени работы алгоритма E

на входах длины n.

Определение 55 «Полиномиальный в среднем (грубо)» Алгоритм A называется полиномиальным в среднем,

если среднее время его работы ограничено полиномом от длины входа, т.е. существует константа c > 0

такая, что E

= O(n

Замечание. Необходимо подчеркнуть, что в теоретических работах, касающихся теории сводимости и сложности в

среднем, полиномиальность в среднем принято определять по другому. Причина состоит в том, что приведенное выше

определение слишком чувствительно: изменение T на T

(типичная оценка при симуляции одной вычислительной мо-

дели на другой) может привести к тому, что алгоритм полиномиальный в среднем, скажем на модели RAM, не является

полиномиальным в среднем на машине Тьюринга.

Упражнение 50 Приведите пример функции T и распределения исходных данных P

(I), для которых T яв-

ляется полиномиальной в среднем, а T

— нет.

Эту ситуацию нельзя признать удовлетворительной, поскольку ничего подобного не происходит при анализе сложности

по худшему случаю: определение полиномиального алгоритма не зависит от выбранной модели вычислений.

Поэтому в теоретических работах, касающихся теории сводимости и сложности в среднем, используют обычно

другое определение:

Определение 56 «Полиномиальный в среднем» Алгоритм называется полиномиальным в среднем, если су-

ществует константа ε > 0 такая, что E

= O(n), где T — время работы алгоритма.

Тем не менее, обычно при анализе конкретных алгоритмов, используют определение 55 «Полиномиальный в сред-

нем (грубо)», имея в виду конкретную модель вычислений (обычно RAM).

Задача 23 «Упаковка» (Packing)

Дано конечное множество L из m элементов и система его подмножеств S

, . .., S

. Требуется найти

максимальную по числу подмножеств подсистему попарно непересекающихся подмножеств.

Эта задача эквивалентна следующей 0 − 1 целочисленной линейной программе

cx → max (3.1)

Ax ≤ b

∀i x

∈ {0, 1}

В этой целочисленной линейной программе n столбцов-переменных x

, . . . , x

соответствуют подмножествам S

, . . . , S

и их включению в решение, вектор стоимости и вектор ограничений: c = (1, . . . , 1), b = (1, . . . , 1). (0, 1)-матрица A

(размера m × n) описывает состав каждого подмножества (или принадлежность каждого из m предметов, заданным n

подмножествам). Проще говоря, матрица A является матрицей инцидентности семейства S

, . .. , S

подмножеств

множества L.

Напомним определения:

Определение 57 Элемент l

и подмножество S

инцидентны, если l

∈ S

Определение 58 Матрицей инцидентности для семейства S

, . .., S

подмножеств множества L называется

(0, 1)-матрица A = (a

) размером m × n, построенная по следующему правилу: a

= 1 в том и только в том

случае, когда элемент l

∈ L и подмножество S

инцидентны.

Это позволяет при изучении задач о покрытии/упаковке пользоваться как терминологией подмножеств конечного

множества, так и вести рассмотрения в терминах (0, 1)-матриц.

Векторы стоимости и ограничений — состоящие полностью из единиц векторы размерности n и m соответственно.

Таким образом m строк-ограничений, соответствующих m предметам, очевидным образом выражают ограничение на

непересекаемость выбранных подмножеств ни по одному предмету, а целевая функция равна числу таких подмножеств.

В литературе задача с ЦЛП постановкой 3.1 (с возможностью выбора произвольных неотрицательных целочислен-

ных векторов c и b), также встречается под названием «Упаковка подмножеств». Известно, что задача 23 «Packing»

NP-полна [Joh90].

Тривиальный метод решения задачи 23 «Packing» — полный перебор, всех 2

наборов подмножеств, с проверкой

на совместность и выбором набора содержащего наибольшее число подмножеств.

Более прогрессивное решение — ограничить перебор по допустимым решениям задачи, применив метод динами-

ческого программирования. Обозначим через T (j) множество всех допустимых булевых векторов для системы (3.1) с

n−j нулевыми последними компонентами и через e

- вектор размерности n с единичной j-й компонентой и остальны-

ми нулевыми компонентами. Тогда можно строить множество допустимых решений T (j) на основе множества T (j −1),

пытаясь добавить множество j ко всем допустимым решениям из T (j).

Более формально это описано в алгоритме 28 «Упаковка-ДинПрог».

Нетрудно убедиться, что сложность алгоритма есть O(mn|T (n)|). Действительно — внешний цикл O(n), внутрен-

ний — O(|T (n)|), проверка на допустимость нового решения — O(m) (если непонятно, обязательно подумайте почему).

Здесь x ≤ y обозначает покомпонентное сравнение векторов.

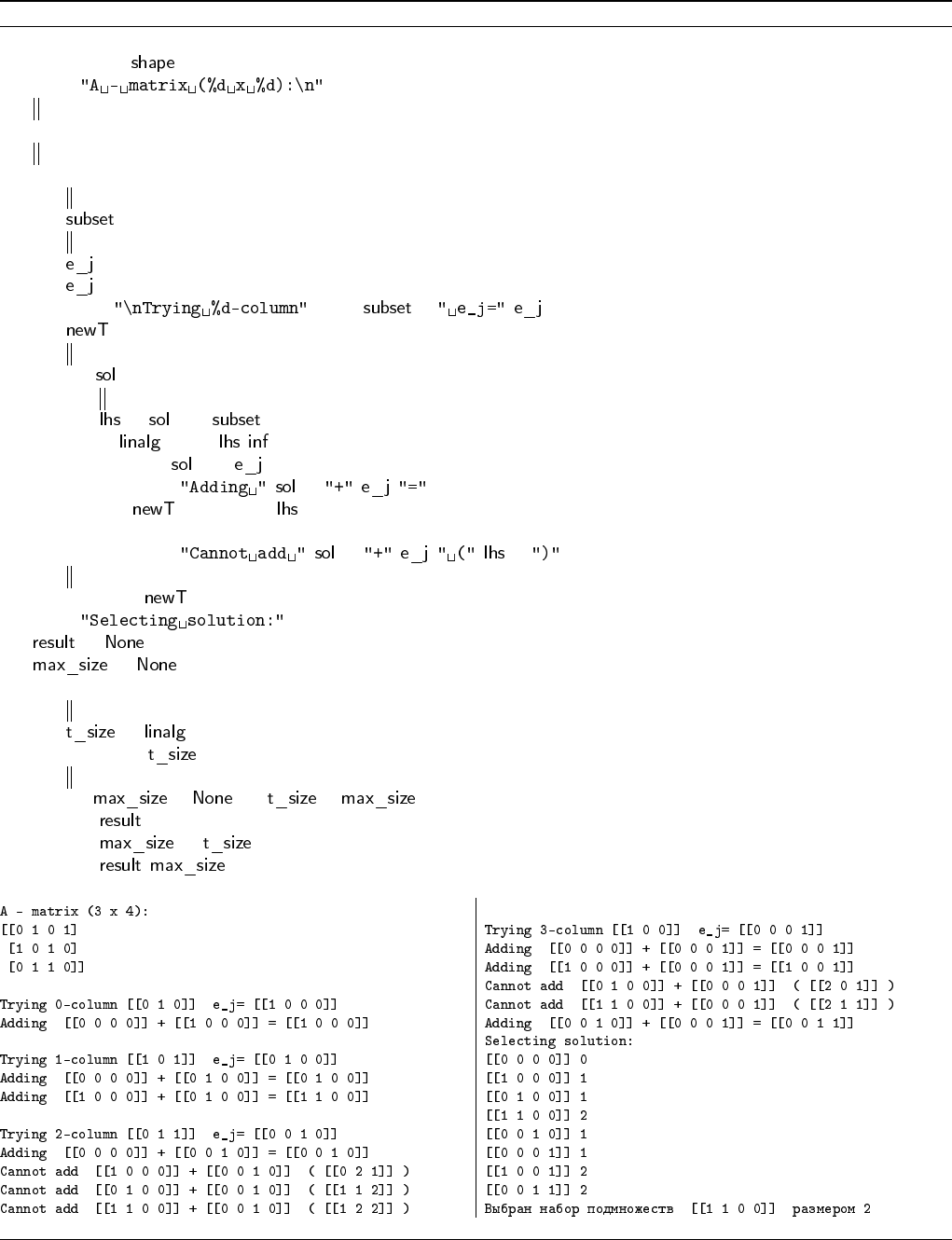
Алгоритм 28 Динамическое программирование для задачи «Упаковка»

def packing_dylp (A) :

(m, n) ← A.

print % (m, n), A

T - множество допустимых решений - список пар (строка-решение,столбец-LHS).

T ← [(mat (zeros (n)), mat (zeros (m)).T )]

Цикл по всем подмножествам.

for j ∈ xrange (n):

Пробуем добавить подмножество j к множеству допустимых решений. subset - j-ое подмножество.

← A[: , j]

- вектор-строка с единицей на j-той позиции

← mat (zeros (n))

[: , j] ← 1

print % (j), .T, ,

← [ ]

Для каждого частичного решения

for ∈ T :

Вычисляем левую часть

← [1] +

if .norm ( , ) < 2:

k ← [0] +

print , [0], , , , k

.append ((k, ))

else:

print , [0], , , , .T,

Добавляем новые частичные решения к основному множеству.

T ← T +

←

for t ∈ T :

для каждого частичного решения, вычисляем его размер

← .norm (t[0].T, 1)

print t[0],

ищем набор наибольшего размера

if ( = ) ∨ ( > ):

← t[0]

←

return ( , )