Кузюрин Н.Н. Фомин С.А. Сложность комбинаторных алгоритмов. Курс лекций
Подождите немного. Документ загружается.

Упражнение 51 Укажите как надо организовать вычисление, чтобы проверка на допустимость нового ре-
шения имела сложность O(m).
Таким образом, сложность алгоритма существенно зависит от размера множества допустимых решений, возника-
ющих при выполнении алгоритма.
Упражнение 52 Какие входные данные для алгоритма 28 «Упаковка-ДинПрог» заставят его работать экс-
поненциально долго? А какие — за O(n
3
)?
Однако, можно показать, что алгоритм 28 «Упаковка-ДинПрог» может быть полиномиальным в среднем, т.е. ра-
ботать эффективно на некотором случайном распределении входных данных.
Предположим, что все элементы a
ij
матрицы ограничений из (3.1) являются независимыми случайными величина-
ми, принимающими значения {0, 1}, причем для всех i, j выполнено
P {a
ij
= 1} = p, P {a
ij
= 0} = 1 − p.
При этом время работы алгоритма является случайной величиной, зависящей от исходных данных, и под средним
временем понимается математическое ожидание времени работы алгоритма.
Теорема 23 Пусть для входных данных задачи 23 «Packing» выполнено условие
mp
2
≥ ln n (3.2)
Тогда алгоритм 28 «Упаковка-ДинПрог» является полиномиальным в среднем.
Доказательство Математическое ожидание времени работы алгоритма — O(nmE|T (n)|). Поэтому для доказатель-
ства теоремы 23 достаточно будет оценить сверху математическое ожидание размера множества T (n).
Вероятность P (k) того, что некоторый вектор x
k
с k единичными компонентами и n − k нулевыми компонентами
является допустимым решением (3.1) (то есть удовлетворяет всем ограничениям в (3.1)) можно оценить сверху следу-
ющим образом:
P (k) =
m
Y
i=1
p
i
(k),
где p
i
(k) — вероятность выполнения i-неравенства для x
k
:
p
i
(k) ≡ P
n
X
j=1
a
ij
x
k
j
≤ 1
≤ P
k
X
j=1
a
ij
≤ 1
,
откуда (при k > 1)
P (k) ≤
m
Y
i=1
P
k
X
j=1
a
ij
≤ 1
=
m
Y
i=1
P
k
X
j=1
a
ij
= 0
+ P
k
X
j=1
a
ij
= 1
=
m
Y
i=1
(1 − p)
k
+ kp(1 − p)
k−1
=
m
Y
i=1
(1 − p)
k−1
(1 + p(k −1)) ≤
m
Y
i=1
(1 − p)
k−1
(1 + p)
k−1
=
m
Y
i=1
(1 − p
2
)
k−1
≤
m
Y
i=1
e
−p
2
(k−1)
= e
−mp
2
(k−1)
Упражнение 53 Докажите, что E|T (n)| ≤
P
n
k=0
n
k
P (k).
Следовательно, мы можем оценить математическое ожидание мощности T (n) следующим образом
E|T (n)| ≤
n
X
k=0
n
k
P (k) = 1 +
n
X
k=1
n
k
P (k) = 1 + n +
n
X
k=2
n
k
P (k)
= 1 + n +
n
X
k=2
n
k
e
−mp
2
(k−1)
≤ 1 + n +
n
X
k=2
e
k ln n−mp
2
(k−1)
= 1 + n + n
n
X
k=2
e
(k−1)(ln n−mp
2
)
91
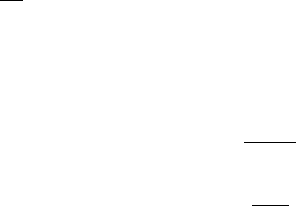
При условии mp
2
≥ ln n в последней сумме каждый член не превосходит 1. Это и означает, что E|T (n)| = O(n
2
).2
В заключение отметим, что из полученных результатов вытекает не только полиномиальный в среднем алгоритм
для задачи оптимизации (3.1), но и полиномиальный в среднем алгоритм для, вообще говоря, более трудной задачи
подсчета числа целых точек в многограннике (3.1).
3.1.2 Точность жадного алгоритма для почти всех исходных данных
Анализ точности алгоритмов в типичном случае. Асимптотическая точность жадного алгоритма в зада-
че о покрытии для «почти всех исходных данных»
Ранее мы доказали, что для задачи о покрытии жадный алгоритм (см. раздел 2.1.1) в худшем случае гарантирует
нахождение покрытия, размер которого превосходит размер минимального покрытия не более чем в логарифмическое
число раз (по m).
Наша цель сейчас — показать, что для «типичных данных» (в отличие от худшего случая, см. упражнение 38) это
отношение близко к единице, т.е. размер покрытия, найденного жадным алгоритмом, почти равен размеру минималь-
ного покрытия.
Как и в предыдущем разделе, мы будем использовать формулировку задачи о покрытии на языке (0, 1)-матриц и
целочисленных линейных программ:
cx → min (3.3)
Ax ≥ b
∀i x
i
∈ {0, 1}
В этой целочисленной линейной программе n столбцов-переменных x
1
, . . . , x
n
соответствуют подмножествам S
1
, . . . , S
n
и их включению в решение-покрытие. Матрица A также является матрицей инцидентности, а векторы стоимости и
ограничений — также векторы размерности n и m соответственно, состоящие полностью из единиц.
Таким образом, m строк-ограничений, соответствующих m предметам, очевидным образом выражают ограничение
на обязательное включение предмета хотя бы в одно из покрывающих подмножеств, а целевая функция равна числу
таких подмножеств.
Как и в разделе 3.1.1, предположим, что A = (a
ij
) — случайная (0,1)-матрица, такая, что для всех i, j выполнено
P {a
ij
= 1} = p, P {a
ij
= 0} = 1 − p.
Пусть R(G) =
Z
G
M
, где Z
G
— величина покрытия найденного жадным алгоритмом, а M — величина минимального
покрытия. Наш основной результат заключается в следующей теореме.
Теорема 24 Пусть вероятность p фиксирована, 0 < p < 1. Пусть для задачи (3.3) со случайной матрицей A
определенной выше выполнены условия:
ln ln n
ln m
→ 0 при n → ∞, (3.4)
ln m
n
→ 0 при n → ∞. (3.5)
Тогда для любого фиксированного ε > 0
P{R(G) ≤ 1 + ε} → 1 при n → ∞.
Заметим, что при m = cn, где c — некоторая константа, условия (3.4) и (3.5) теоремы 24 выполнены автоматически.
Доказательство Сначала докажем нижнюю оценку размера минимального покрытия.
Пусть X — случайная величина, равная числу покрытий размера
l
0
= −d(1 − δ) ln m/ ln(1 − p)e,
тогда
EX =
n
l
0
P (l
0
),
где P (l
0
) — вероятность того, что фиксированные l
0
столбцов являются покрытием A. Нетрудно видеть (убедитесь, что
это действительно нетрудно!), что
P (l
0
) =
1 − (1 − p)
l
0
m
≤ exp{−m(1 − p)
l
0
}.
92

Используя неравенство
n
k
≤ n
k
, получаем
ln EX ≤ l
0
ln n − m(1 − p)
l
0
≤ −
ln m
ln(1 − p)
ln n − m exp
−(1 − δ) ln(1 − p)
ln m
ln(1 − p)
≤ −
ln m
ln(1 − p)
ln n − mm
−1
m
δ
≤ −
ln m
ln(1 − p)
ln n − m
δ
.
Нетрудно проверить, что для любого фиксированного 0 < δ < 1 при условиях (3.4) последнее выражение стремится
к −∞ при n стремящемся к бесконечности.
Таким образом, вероятность того, что нет покрытия размера l
0
в случайной (0, 1)-матрице A стремится к 1, по-
скольку (согласно неравенству Чебышева)
P{X ≥ 1} ≤ EX → 0.
Последнее означает, что M ≥ l
0
.
Теперь докажем верхнюю оценку размера покрытия построенного жадным алгоритмом.
Используем следующую известную лемму [AS92] о вероятности больших уклонений для сумм независимых случай-
ных величин.
Лемма 21 Пусть Y — сумма n независимых случайных величин, каждая из которых принимает значение 1 с
вероятностью p и 0 с вероятностью 1 − p. Тогда
P{|Y − np| > δnp} ≤ 2 exp{−(δ
2
/3)np}.
По этой лемме вероятность того, что некоторый фиксированный столбец содержит менее чем (1 −δ)pn единиц (или
более чем (1 + δ)pn единиц) оценивается сверху так:
P
bad
≤ 2 exp{−(δ
2
/3)np},
и математическое ожидание числа таких столбцов не превосходит mP
bad
. Нетрудно видеть, что
mP
bad
≤ 2 exp{ln m − (δ
2
/3)np} = 2 exp{ln m − O(1)n} → 0, при n → ∞,
по условию (3.5). Следовательно, первое неравенство Чебышева P {X ≥ 1} ≤ EX влечет, что вероятность события
«каждый столбец содержит не менее (1 − δ)pn единиц» стремится к 1.
Теперь мы можем почти дословно повторить получение верхней оценки размера покрытия, построенного жадным
алгоритмом, в худшем случае.
Пусть N
t
— число непокрытых строк после t-го шага жадного алгоритма. Имеем:
N
t
≤ N
t−1
−
N
t−1
(1 − δ)pn
n
= N
t−1
(1 − (1 − δ)p)
≤ N
0
(1 − (1 − δ)p)
t
= m(1 − (1 − δ)p)
t
.
Найдем максимальное t при котором еще есть непокрытый элемент:
m(1 − (1 − δ)p)
t
≥ 1
Получим:
ln m + t ln(1 − (1 − δ)p) ≥ 0,
или
t ≥ −
ln m
ln(1 − (1 − δ)p)
Отсюда получается верхняя оценка мощности «жадного покрытия» в типичном случае:
Z
G
≤ 1 +
ln m
ln
1
1−p(1−δ)
.
93

Упражнение 54 Докажите, что комбинируя это неравенство с нижней оценкой, можно получить что для
любого фиксированного ε > 0 и достаточно больших n
R(G) ≤ 1 + ε.
2
3.1.3 Полиномиальный в среднем алгоритм для задачи о рюкзаке
Рассмотрим снова классическую задачу о рюкзаке.
Вход: Положительные веса w
1
, . . . , w
n
, стоимости p
1
, . . . , p
n
, размер рюкзака B.
Выход: Подмножество S ⊆ [n] := {1, 2, . . . , n} такое что
P
i∈S
w
i
≤ B и
P
i∈S
p
i
— максимально.
Известно, что эта задача NP-трудна, если рассматривать ее с точки зрения худшего случая. Однако, было отмече-
но, что на практике некоторые из известных алгоритмов ее решения чрезвычайно эффективны. Одна из самых извест-
ных аналогий — это знаменитый симплекс-метод решения задачи линейного программирования, который на некоторых
входах работает экспоненциальное время, но в большинстве практических случаев чрезвычайно эффективен. Теоре-
тическое объяснение этого феномена заключается в том, что симплекс метод является полиномиальным в среднем
алгоритмом. Аналогичное положение (как выяснилось совсем недавно) имеет место быть и для задачи о рюкзаке.
Алгоритм Немхаузера-Ульмана
Мы рассмотрим сейчас алгоритм Немхаузера-Ульмана, основанный на методе динамического программирования, для
решения этой задачи и проанализируем его.
Определение: Подмножество S ⊆ [n] веса w(S) =
P
i∈S
w
i
и стоимости
P
i∈S
p
i
доминирует другое подмножество
T ⊆ [n] если w(S) ≤ w(T ) и p(S) ≥ p(T ).
Для i ∈ [n] пусть S(i) обозначает последовательность всех доминирующих подмножеств над 1, 2, . . . , i. Будем пред-
полагать, что множества в S(i) упорядочены по возрастанию их весов. Зная S(i) нетрудно найти S(i + 1) следующим
образом: сделаем еще одну копию S(i) и добавим элемент i+1 к каждому из элементов скопированного массива. Далее
сливаем два последовательных списка, удаляя множества доминируемые некоторым множеством из объединения двух
последовательностей. В результате получим S(i + 1). Обозначим q(n) = |S(n)|.
Лемма 1. Алгоритм Немхаузера-Ульмана вычисляет оптимум в задаче о рюкзаке за время
O (n · q(n)) .
Анализ
Теорема. Пусть веса w
i
являются произвольными положительными числами, а стоимости p
i
являются случайными
независимыми величинами равномерно распределенными на отрезке [0,1], и пусть q обозначает число доминирующих
множеств для всех n предметов. Тогда E[q] = O(n
3
).
Доказательство. Пусть m = 2
n
и S
1
, . . . , S
m
обозначают последовательность всех подмножеств множества [n],
перечисленных в порядке неубывания их весов. Пусть стоимость подмножества S
u
есть P
u
=
P
i∈S
u
p
i
. Для любого
2 ≤ u ≤ m, определим ∆
u
= max
k∈[u]
P
k
− max
k∈[u−1]
P
k
≥ 0.
Факт 1. Для любого u ≥ 2, S
u
— доминирующее множество тогда и только тогда когда ∆
u
> 0.
Имеем:
E[q] = P
1
+
m
X
u=2
Pr[∆
u
> 0].
Таким образом, для получения верхней оценки E[q] достаточно получить верхнюю оценку для
P
m
u=2
Pr[∆
u
> 0].
Для получения верхней оценки оценим E[P
m
]. С одной стороны,
E[P
m
] = P
1
+
m
X
u=2
E[∆
u
] =
m
X
u=2
Pr[∆
u
> 0]E[∆
u
| ∆
u
> 0].
С другой стороны, E[P
m
] = n/2. Справедлива следующая
Лемма 2. Для любого u ∈ {2, . . . , m}, E[∆
u
| ∆
u
> 0] ≥
1
32n
2
.
Отсюда следует, что
n/2 = E[P
m
] =
m
X
u=2
Pr[∆
u
> 0]E[∆
u
| ∆
u
> 0] ≥
m
X
u=2
Pr[∆
u
> 0] ·
1
32n
2
,
94

или E[q] = 1 +
P
m
u=2
Pr[∆
u
> 0] ≤ 16n
3
+ 1.
Таким образом, для получения окончательного результата остается доказать лемму 2.
Доказательство леммы 2. Зафиксируем u ∈ {2, . . . , m}. Заметим, что
E[∆
u
| ∆
u
> 0] ≥ Pr[∆
u
≥
1
16n
2
| ∆
u
> 0] ·
1
16n
2
.
Значит, достаточно доказать, что Pr[∆
u
≥
1
16n
2
| ∆
u
> 0] ≥
1
2
. Для каждого k ∈ [u − 1] положим X
k
= S
u
\ S
k
и
Y
k
= S
k
\ S
u
. Имеем:
Pr[∆
u
≥
1
16n
2
| ∆
u
> 0] = Pr
"
∀k :
X
i∈S
u
p
i
≥
X
i∈S
k
p
i
+
1
16n
2
| ∀k :
X
i∈S
u
p
i
>
X
i∈S
k
p
i
#
=
= Pr
"
∀k :
X
i∈X
k
p
i
≥
X
i∈Y
k
p
i
+
1
16n
2
| ∀k :
X
i∈X
k
p
i
≥
X
i∈Y
k
p
i
#
,
где квантор всеобщности распространяется на все элементы k ∈ [u − 1]. Без ограничения общности можно считать,
что S
u
= [t]. Рассмотрим два класса случайных переменных {p
1
, . . . , p
t
} и {p
t+1
, . . . , p
n
}. Пусть значения переменных
из второго класса фиксированы произвольным образом. Оценим вероятность того, что хотя бы одна из переменных из
первого класса мала.
Pr
"
∃j ∈ [t] : p
j
≤
1
4n
| ∀k :
X
i∈X
k
p
i
≥
X
i∈Y
k
p
i
#
≤
X
j∈[t]
Pr
"
p
j
≤
1
4n
| ∀k :
X
i∈X
k
p
i
≥
X
i∈Y
k
p
i
#
≤
≤
X
j∈[t]
Pr
p
j
≤
1
4n
=
t
4n
≤
1
4
.
Далее предположим, что p
j
≥
1
4n
, для любого j ∈ [t]. Пусть L
k
=
P
i∈X
k
p
i
. При нашем предположении L
k
≥
1
4n
, для
любого k ∈ [u − 1], поскольку каждое множество X
k
содержит по крайней мере один элемент размера не менее
1
4n
.
При наших предположениях о L
k
мы анализируем Pr
∆
u
<
1
16n
2
| ∆
u
> 0
. Для того, чтобы компенсировать слу-
чай, когда наше предположение не имеет места, мы докажем что эта вероятность не превосходит 1/4 (вместо 1/2). В
частности, перепишем уравнение (1) и докажем, что
Pr
"
∀k :
X
i∈Y
k
p
i
≤ L
k
−
1
16n
2
| ∀k :
X
i∈Y
k
p
i
≤ L
k
#
≥
3
4
,
для произвольного фиксированного L
k
≥
1
4n
, где вероятность рассматривается по случайному выбору значений пере-
менных p
t+1
, . . . , p
n
.
Рассмотрим теперь геометрические интерпретации. Рассмотрим (n − t)-мерные политопы:
A =
(
(p
t+1
× . . . × p
n
) ∈ [0, 1]
n−t
| ∀k :
X
i∈Y
k
p
i
≤ L
k
−
1
16n
2
)
,
B =
(
(p
t+1
× . . . × p
n
) ∈ [0, 1]
n−t
| ∀k :
X
i∈Y
k
p
i
≤ L
k
)
.
Ясно, что A ⊆ B. Поскольку распределение равномерное,
Pr
∆
u
≥
1
16n
2
| ∆
u
> 0
=
vol(A ∩ B)
vol(B)
=
vol(A)
vol(B)
,
где vol(
˙
) обозначает объем соответствующего политопа. В терминах объемов нам надо показать, что vol(A) ≥
3
4
vol(B).
Идея заключается в измельчении политопа B равномерно по всем размерностям пока измельченный политоп не
будет содержаться в политопе A. Для ε ∈ [0, 1] определим
B
ε
=
(
(p
t+1
× . . . × p
n
) ∈ [0, 1 − ε]
n−t
| ∀k :
X
i∈Y
k
p
i
≤ (1 − ε)L
k
)
.
95

Очевидно, B = B
0
и, в общем случае, B
ε
может быть получен разбиением B по каждому измерению на множитель
1 − ε. Поскольку размерность равна n − t, vol(B
ε
) = (1 − ε)
n−t
vol(B).
Далее мы исследуем вопрос о том, как выбрать ε так чтобы B
ε
⊆ A. Заметим, что L
k
(1−
1
4n
) ≤ L
k
−
1
16n
2
, поскольку
L
k
≥
1
4n
. Полагая ε =
1
4n
, получаем что B
ε
⊆ A.
Далее имеем:
vol(A) ≥ vol(B
ε
) = (1 − ε)
n−t
vol(B) ≥
(1 − ε(n − t))vol(B) ≥
3
4
vol(B),
что завершает доказательство леммы.
3.2 Вероятностные алгоритмы.
Напомним, что формальные (и неформальные) определения вероятностных алгоритмов и их классов мы рассматривали
в разделе 1.4.
3.2.1 Алгоритм Фрейвалда
Один из первых примеров вероятностных алгоритмов, более эффективных чем детерминированные, был предложен
Фрейвалдом (см. [MR95]) для задачи проверки матричного равенства AB = C. Обычный детерминированный алгоритм
заключается в перемножении матриц A и B и сравнении результата с C.
Сложность такого алгоритма есть O(n
3
) при использовании стандартного алгоритма умножения матриц размера
n × n, и O(n
2.376
) при использовании лучшего из известных быстрых алгоритмов матричного умножения.
Вероятностный алгоритм Фрейвалда для этой задачи имеет сложность O(n
2
) и заключается в умножении левой и
правой частей на случайный булев вектор x = (x
1
, . . . , x
n
) с последующим сравнением полученных векторов. Алго-
ритм выдает ответ, что AB = C, если ABx = Cx и является алгоритмом типа Монте-Карло с односторонней ошиб-
кой [MR95]. При этом ABx вычисляется как A(Bx), что и обеспечивает оценку сложности алгоритма O(n
2
).
Корректность алгоритма обеспечивается следующей теоремой.
Теорема 25 Пусть A, B, и C — n ×n матрицы над полем F
2
, причем AB 6= C. Тогда для случайного вектора x
выбранного случайно и равномерно из {0, 1}
n
,
P {ABx = Cx} ≤ 1/2.
Доказательство Пусть D = AB −C. Мы знаем, что D — не полностью нулевая матрица и хотим оценить вероятность
того, что Dx = 0. Без ограничения общности можно считать, что ненулевые элементы имеются в первой строке и они
располагаются перед нулевыми. Пусть d — вектор, равный первой строке матрицы D, и предположим, что первые k
элементов в d — ненулевые.
P{Dx = 0} ≤ P{d
T
x = 0}.
Но, d
T
x = 0 тогда и только тогда, когда
x
1
=
−
P
k
i=2
d
i
x
i
d
1
Для каждого выбора x
2
, . . . , x
k
правая часть этого равенства фиксирована и равна некоторому v > 0. Вероятность, что
x
1
равно v, не превосходит 1/2, поскольку x
1
равномерно распределено на двухэлементном множестве ({0, 1}).
2
Классическим примером задачи, где вероятностные алгоритмы успешно применяются, является задача проверки
тождеств для многочлена от многих переменных:
Задача 24 Верно ли для заданного полинома P (x
1
, . . . , x
n
), что P (x
1
, . . . , x
n
) ≡ 0?
Следующая лемма (См. [MR95]) по сути описывает вероятностный Монте-Карло алгоритм с односторонней ошиб-
кой.
2
элементы матрицы ∈ F
96
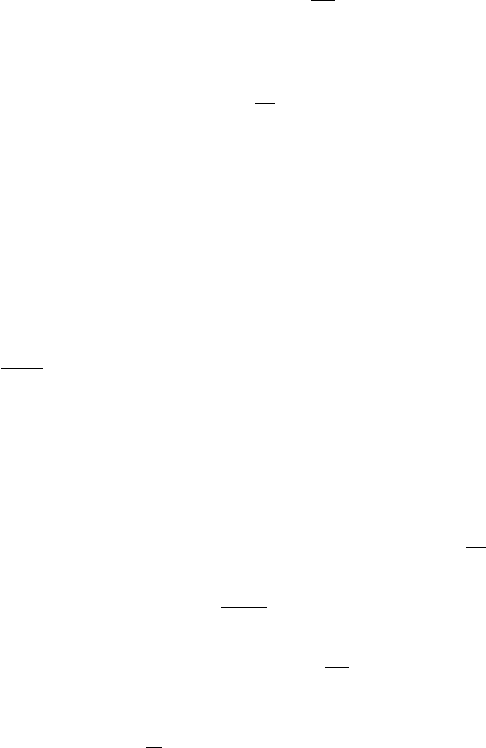
Лемма 22 Пусть Q(x
1
, . . . , x
n
) — многочлен от многих переменных степени d над полем F и пусть S ⊆ F —
произвольное подмножество. Если r
1
, . . . , r
n
выбраны случайно, независимо и равномерно из S, то
P (Q(r
1
, . . . , r
n
) = 0 | Q(x
1
, . . . , x
n
) 6≡ 0) ≤
d
|S|
.
Доказательство По индукции по n.
Базисный случай n = 1 включает полиномы от одной переменной Q(x
1
) степени d. Поскольку каждый такой поли-
ном имеет не более d корней, вероятность, что Q(r
1
) = 0 не превосходит
d
|S|
.
Пусть теперь предположение индукции верно для всех полиномов, зависящих от не более n − 1 переменной.
Рассмотрим полином Q(x
1
, . . . , x
n
) и разложим его по переменной x
1
Q(x
1
, . . . , x
n
) =
k
X
i=0
x
i
1
Q
i
(x
2
, . . . , x
n
),
где k ≤ d — наибольшая степень x
1
в Q.
Предполагая, что Q зависит от x
1
, имеем k > 0, и коэффициент при x
k
1
, Q
k
(x
2
, . . . , x
n
) не равен тождественно нулю.
Рассмотрим две возможности.
Первая — Q
k
(r
2
, . . . , r
n
) = 0. Заметим, что степень Q
k
не превосходит d − k, и по предположению индукции
вероятность этого события не превосходит
(d−k)
|S|
.
Вторая — Q
k
(r
2
, . . . , r
n
) 6= 0. Рассмотрим следующий полином от одной переменной:
q(x
1
) = Q(x
1
, r
2
, r
3
, . . . , r
n
) =
k
X
i=0
Q
i
(r
2
, . . . , r
n
)x
i
.
Полином q(x
1
) имеет степень k, и не равен тождественно нулю, т.к. коэффициент при x
k
1
есть Q
k
(r
2
, . . . , r
n
). Базо-
вый случай индукции дает, что вероятность события q(r
1
) = Q(r
1
, r
2
, . . . , r
n
) = 0 не превосходит
k
|S|
.
Мы доказали два неравенства:
P{Q
k
(r
2
, . . . , r
n
) = 0} ≤
d − k
|S|
;
P{Q(r
1
, r
2
, . . . , r
n
) = 0| Q
k
(r
2
, . . . , r
n
) 6= 0} ≤
k
|S|
.
Используя результат следующего упражнения: покажите, что для любых двух событий E
1
, E
2
,
P{E
1
} ≤ P{E
1
| E
2
} + P{E
2
},
мы получаем, что вероятность события Q(r
1
, r
2
, . . . , r
n
) = 0 не превосходит суммы двух вероятностей (d − k)/|S| и
k/|S|, что дает в сумме желаемое d/|S|. 2
Упражнение 55 Имеется квадратная, n × n матрица A, элементами которой являются линейные функции
f
ij
(x) = a
ij
x + b
ij
.
Придумайте Монте-Карло алгоритм с односторонней ошибкой, для проверки этой матрицы на вырож-
денность (detA ≡ 0).
Еще одним примером успеха вероятностных алгоритмов является разработка эффективных вероятностных алго-
ритмов проверки простоты числа: для натурального числа n заданного в двоичной системе, определить является ли оно
простым [SV77]. Только в 2002 г. для этой задачи удалось построить полиномиальный детерминированный алгоритм.
Одной из многочисленных областей, где широко применяются вероятностные алгоритмы, являются параллельные
вычисления. Эффективным параллельным алгоритмом (или NC-алгоритмом) называется алгоритм, который на много-
процессорной RAM (так называемой PRAM) с числом процессоров не превосходящих некоторого полинома завершает
работу за время ограниченное полиномом от логарифма длины входа. Построение эффективного детерминированного
параллельного алгоритма (NC-алгоритма) для нахождения максимального паросочетания в двудольном графе являет-
ся одной из основных открытых проблем в теории параллельных алгоритмов. Удалось, однако, построить эффективный
параллельный вероятностный алгоритм нахождения максимального паросочетания в двудольном графе (так называе-
мый RNC-алгоритм) [MR95].
97

3.2.2 Вероятностные методы в перечислительных алгоритмах. Подсчет числа выполняю-
щих наборов для ДНФ
В данной лекции мы рассматриваем перечислительные задачи и изучим как вероятностные методы могут быть приме-
нены для решения таких задач. Алгоритм для решения перечислительной задачи берет на вход конкретные входные
данные рассматриваемой задачи (например граф) и в качестве выхода выдает неотрицательное целое являющееся чис-
лом решений задачи (например число гамильтоновых циклов в графе).
Далее мы опишем рандомизированную полиномиальную аппроксимационную схему для задачи подсчета числа вы-
полняющих наборов для данной днф, т.е. число наборов, на которых днф равна 1.
Пусть П - некоторая перечислительная задача, I - вход задачи. Пусть далее #(I) обозначает число различных
решений для входа I задачи П.
Определение 59 Полиномиальной рандомизированной аппроксимационной схемой (PRAS) для пере-
числительной задачи П называется вероятностный алгоритм A, который получая вход I и вещественное
ε > 0, за время полиномиальное от n = |I|выдает в качестве выхода A(I) такое, что
Pr[(1 − ε)#(I) ≤ A(I) ≤ (1 + ε)#(I)] ≥
3
4
.
Определение 60 Полностью полиномиальной рандомизированной аппроксимационной схемой
(FPRAS) называется полиномиальная рандомизированная аппроксимационная схема, время работы кото-
рой ограничено полиномом от n и 1/ε.
Определение. Полностью полиномиальной рандомизированной аппроксимационной схемой с параметрами (ε, δ)
(или кратко (ε, δ)-FPRAS) для перечислительной задачи П называется полностью полиномиальная рандомизирован-
ная аппроксимационная схема, которая на каждом входе I вычисляет ε-аппроксимацию для #(I) с вероятностью не
менее 1 − δ за время полиномиальное от n, 1/ε и log 1/δ.
Перечислительная задача для днф.
Пусть f (x
1
, . . . , x
n
) – булева формула в дизъюнктивной нормальной форме (днф) над множеством булевых пе-
ременных x
1
, . . . , x
n
. Иными словами f = C
1
∨ . . . ∨ C
m
есть дизъюнкция скобок C
i
, где каждая скобка C
i
есть
конъюнкция L
1
∧ . . . ∧ L
k
i
k
i
литералов. Каждый литерал есть либо переменная, либо ее отрицание.
Каждой булевой переменной приписывается значение из {0, 1}. Набор значений переменных a = (a
1
, . . . , a
n
) на-
зывается выполняющим для f если f (a
1
, . . . , a
n
) = 1.
Мы будем обозначать через #f число выполняющих наборов для данной формулы f .
Мы сформулируем более общую задачу и опишем для нее (ε, δ)-FPRAS.
Пусть U – конечное множество известной мощности и пусть f : U → {0, 1} булева функция над U . Положим G =
{u ∈ U | f (u) = 1}. Предположим, что для любого u ∈ U, f(u) можно вычислить эффективно. Предположим также,
что возможно равномерно и случайно выбирать элементы из U. Для простоты будем считать, что обе эти операции
занимают единичное время. Проблема заключается в оценке |G|.
Рассмотрим стандартный метод Монте-Карло и покажем, что он не является (ε, δ)-FPRAS для этой задачи.
1. Проведем N независимых испытаний, в каждом из которых выбирается случайная точка из U с равномерным
распределением. Если в i-м испытании в выбранной точке значение f равно 1, то полагаем y
i
= 1, в противном случае
полагаем y
i
= 0.
2. Рассмотрим сумму независимых случайных величин Y =
P
N
i=1
y
i
. В качестве аппроксимации |G| возьмем вели-
чину
˜
G =
Y
N
|U|.
Заметим, что P {y
i
= 1} = |G|/|U|. Обозначим эту вероятность через p. Справедливо следующее неравенство
Лемма ([MR95]. Пусть x
1
, . . . , x
n
– независимые случайные величины такие, что x
i
принимают значения 0, 1, и
P {x
i
= 1} = p, P {x
i
= 0} = 1 − p. Тогда для X =
P
n
i=1
x
i
и EX = np и для любого 0 < δ < 1, выполнены
неравенства:
P {X − EX > δEX} ≤ exp{−(δ
2
/3)EX}
P {X − EX < −δEX} ≤ exp{−(δ
2
/2)EX}.
Оценим вероятность того, что аппроксимация хорошая.
Pr{(1 − ε)|G| ≤
˜
G ≤ (1 + ε)|G|} = Pr{(1 − ε)|G|N/|U| ≤ Y ≤ (1 + ε)|G|N/|U|} =
Pr{(1 − ε)Np ≤ Y ≤ (1 + ε)Np}.
Применяя неравенства из леммы, получаем:
Pr{(1 − ε)|G| ≤ Z ≤ (1 + ε)|G|} > 1 − 2 exp{−(ε
2
/3)Np}.
98

Накладываем условие, чтобы эта оценка была не меньше 1 − δ, и получаем:
2 exp{−(ε
2
/3)Np} < δ,
что эквивалентно
2
δ
< exp{ε
2
/3Np}
или
N >
1
p
3
ε
2
ln
2
δ
.
Почему полученная оценка не столь хороша? Потому что p может быть экспоненциально мало (например, если
функция равна 1 лишь в одной точке) и тогда число требующихся шагов будет экспоненциально велико.
Покажем как использовать этот метод не напрямую, а после некоторой переработки задачи.
Рассмотрим более общую (по сравнению с задачей о числе выполняющих наборов для днф) задачу.
Пусть V – конечное множество и имеется m его подмножеств H
1
, . . . , H
m
⊆ V удовлетворяющих следующим
условиям:
1. Для любого i, |H
i
| вычислимо в полиномиальное время;
2. Для любого i возможно выбрать случайно и равномерно элемент из H
i
;
3. Для любого v ∈ V возможно за полиномиальное время проверить верно ли, что v ∈ H
i
.
Нашей целью является оценка мощности объединения H = H
1
∪ . . . ∪ H
m
.
Определим U = {(v, i)| v ∈ H
i
}. Нетрудно видеть, что
|U| =
m
X
i=1
|H
i
| ≥ |H|.
Для любого v ∈ H множество покрывающее v определяется так:
cov(v) = {(v, i)| (v, i) ∈ U}.
Мощность покрывающего множества в точности равна числу H
i
, содержащих v. В проблеме подсчета числа выполня-
ющих наборов для днф для набора a = (a
1
, . . . , a
n
), множество cov(a) является множеством скобок выполненных на a
(т.е. равных 1).
Нетрудно проверить следующие простые факты:
1. Число покрывающих множеств равно |H| и покрывающие множества легко вычислить;
2. Имеет место следующее разбиение U: U = ∪
v ∈H
cov(v);
3. |U| легко вычислить как |U| =
P
v ∈H
|cov(v)|;
4 Для любого v ∈ H, cov(v) ≤ m.
Определение. Функция F : U → {0, 1} определяется следующим образом:
F ((v, i)) = 1 тогда и только тогда когда i = min{j| v ∈ H
j
}, и нулю в противном случае.
Множество G определяется так:
G = {(v, j) ∈ U | F ((v, i)) = 1}.
Важное наблюдение заключается в том, что |G| = |H|.
Наша цель теперь заключается в оценке мощности G ⊆ U.
Лемма 1. Справедливо неравенство
ρ =
|G|
|U|
≥
1
m
.
Доказательство. Доказательство использует наблюдения, сделанные выше.
|U| =
X
v ∈H
|cov(v)| ≤
X
v ∈H
m ≤ m|H| = m|G|.
Далее применение стандартной техники метода Монте-Карло позволяет построить (ε, δ)-FPRAS для оценки |G|, и,
следовательно, и для |H|.
Теорема. Метод Монте-Карло дает (ε, δ)-FPRAS для оценки |G| при условии
N ≥
3m
ε
2
ln
2
δ
.
Время полиномиально по N.
99
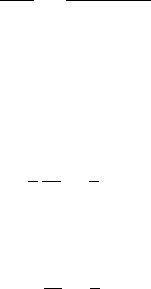
Доказательство. Нам необходимо показать что F можно вычислить в полиномиальное время и можно эффективно
выбирать случайный элемент (равномерно) из U.
Для вычисления F ((v, i)) мы проверяем, верно ли, что набор значений переменных v является выполняющим для
C
i
, но не для C
j
, j < i.
Выбор случайного элемента (v, i) равномерно из U осуществляется в два этапа.
На первом этапе выберем i, 1 ≤ i ≤ m и
Pr[i] =
|H
i
|
|U|
=
|H
i
|
P
m
i=1
|H
i
|
.
На втором этапе элемент v ∈ H
i
выбирается случайно и равномерно. Нетрудно проверить, что справедливо следующее
Утверждение 1. Получаемая пара (v, i) равномерно распределена в U .
Для доказательства достаточно перемножить соответствующие вероятности.
Далее воспользуемся классическим методом Монте-Карло. Из полученных ранее оценок имеем:
N >
1
p
3
ε
2
ln
2
δ
.
Из леммы 1 следует, что 1/p ≤ m, откуда получаем, что достаточно провести N испытаний, где
N > m
3
ε
2
ln
2
δ
.
Это и завершает доказательство теоремы.
Для исходной задачи перечисления выполняющих наборов для данной ДНФ имеем: базовое множество V состоит
из всех двоичных наборов длины n, H
i
состоит из всех наборов, на которых скобка C
i
равна 1 (выполнена). Ясно, что
|H
i
| = 2
n−r
i
, где r
i
– число литералов в скобке C
i
. Нетрудно также организовать случайную выборку элемента из H
i
:
для этого достаточно зафиксировать значения переменных, входящих в конъюнкцию а остальные выбрать случайны-
ми. Проверка, что некоторое v ∈ V принадлежит H
i
, эквивалентно проверке выполнимости скобки (конъюнкции) на
данном наборе. Таким образом, все условия на H
i
выполнены и описанный метод аппроксимации дает (ε, δ)-FPRAS
для оценки числа выполняющих наборов для любой ДНФ.
Упражнения.
1. Докажите упражнение 1.
2. Докажите факт 2: U = ∪
v ∈H
cov(v).
3. Докажите, что для G = {(v, j) ∈ U| f((v, i)) = 1} верно равенство |G| = |H|.
3.2.3 Вероятностный алгоритм Луби нахождения максимального по включению независи-
мого множества в графе
Пусть G = (V, E) – неориентированный граф с n вершинами и m ребрами. Подмножество вершин I ⊆ V называется
независимым в G, если никакое ребро из E не содержит обе своих конечных вершины в I.
Определение: Независимое множество I называется максимальным по включению, если оно не содержится в
качестве собственного подмножества в другом независимом множестве в G.
Напомним, что задача нахождения максимального по мощности независимого множества NP-трудна. Однако, для
нахождения максимального по включению независимого множества существует тривиальный последовательный алго-
ритм с временной сложностью O(m).
Алгоритм Greedy MIS:
Вход: Граф G = (V, E) с V = {1, 2, . . . , n}.
Выход: Максимальное по включению множество I ⊆ V .
1. I := ∅.
2. для v = 1 до n выполнить
если I ∩ Γ(v) = ∅ то I := I ∪ {v}.
Лемма. Алгоритм Greedy MIS завершает работу после O(m) шагов и выдает максимальное по включению неза-
висимое множество, при условии, что граф на вход подается в виде списка смежности.
Проблема заключается в том, чтобы построить эффективный параллельный алгоритм для этой задачи. Мы будем
рассматривать модель PRAM (Parallel RAM), которая состоит из p процессоров с общим набором регистров (ячеек
памяти). Процессоры могут писать в память и читать из памяти независимо друг от друга. Ограничением является лишь
возможность писать или читать из одной ячейки для нескольких процессоров. Мы будем рассматривать самую слабую
модель — EREW PRAM (Exclusive Reed Exclusive Write PRAM), в которой процессоры могут читать одновременно
только из разных ячеек и писать в разные ячейки.
100
