Кузюрин Н.Н. Фомин С.А. Сложность комбинаторных алгоритмов. Курс лекций

Подождите немного. Документ загружается.

Определение 26 Класс сложности RP

strong

состоит из всех языков L для которых существует полиноми-

альная ВМТ M, и полином p(·), такие что:

x ∈ L ⇒ P [M(x) = 1] ≥ 1 − 2

−p(|x|)

x /∈ L ⇒ P [M(x) = 1] = 0

Первоначально, кажется, что RP

weak

некоторая релаксация (ослабление ограничений), класса RP, а RP

strong

наоборот, усиление ограничений, и, по крайней мере:

strong

⊆ RP ⊆ RP

weak

Однако, оказывается, все это определения одного и того же класса.

Лемма 10 RP

weak

= RP

strong

= RP

Доказательство Достаточно показать, что RP

weak

⊆ RP

strong

, для чего мы покажем, как для любого языка L ∈

weak

, из машины M

weak

(машина M из определения 25) сделать машину M

strong

, соответствующую определению 26.

Действуем, как и в более простом случае леммы 9 — для данного x машина M

strong

запускает t раз машину M

weak

, и

возвращает Логическое ИЛИ от всех результатов запуска. Также, как и в случае леммы 9, возможна только ошибка

второго рода, причем ее вероятность (если x ∈ L):

P (M

strong

(x) = 0) = (P (M

weak

(x) = 0))

t(|x|)



1 −

p(|x|)



t(|x|)

Осталось найти необходимое «для разгона» количество запусков:



1 −

p(|x|)



t(|x|)

≤ 2

−p(|x|)

откуда получаем:

t(|x|) ≥ −

log 2 p(|x|)

log



1 −

p(|x|)



≥ log 2 · p

(|x|).

Т.е. за полиномиальное время мы усиливаем вероятность с «полиномиально малой» до «полиномиально близкой к

единице». 2

1.4.2 Класс BPP. Эффективное распознавание с двухсторонней ошибкой.

Теперь рассмотрим, что происходит, если допустить возможность двухсторонних ошибок, т.е. ошибок первого и второго

рода. Определим класс языков, эффективно распознаваемых на ВМТ с двухсторонней ошибкой.

Определение 27 Класс сложности BPP (Bounded-Probability Polynomial-time) состоит из всех языков L для

которых существует полиномиальная ВМТ M, такая что:

x ∈ L ⇒ P [M(x) = 1] ≥

x /∈ L ⇒ P [M(x) = 0] ≥

Из определения видно, что класс BPP замкнут относительно дополнения.

По опыту раздела 1.4.1, читатель ожидает обобщений определения класса BPP, без магической константы «

», и

мы его не разочаруем. Итак, предоставим «свободное» и «жесткое» определения класса BPP.

Определение 28 Класс сложности BPP

weak

состоит из всех языков L для которых существует:

1. полиномиально вычислимая функция f : N 7→ [0, 1];

2. положительный полином p(·);

3. полиномиальная ВМТ M;

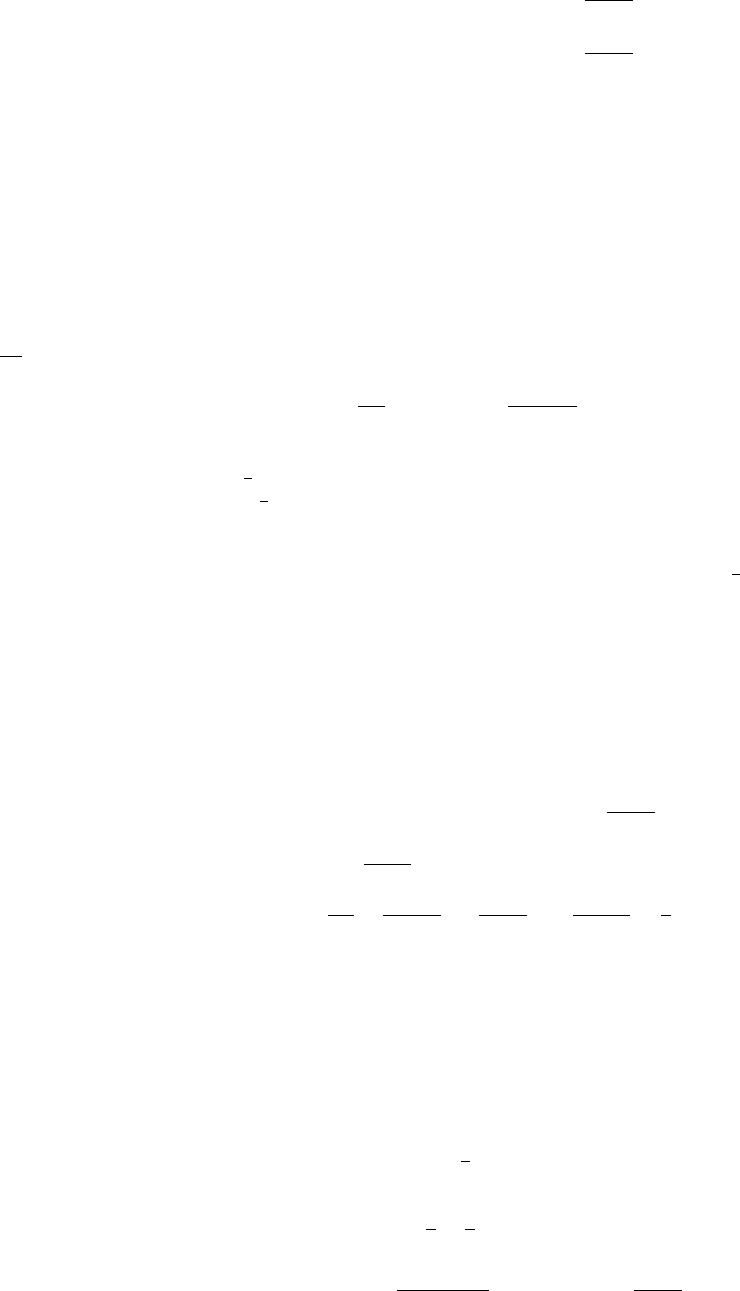
такие что:

x ∈ L ⇒ P [M(x) = 1] ≥ f (|x|) +

p(|x|)

x /∈ L ⇒ P [M(x) = 1] < f(|x|) −

p(|x|)

Определение 29 Класс сложности BPP

strong

состоит из всех языков L для которых существует полиноми-

альная ВМТ M, и полином p(·), такие что:

x ∈ L ⇒ P [M(x) = 1] ≥ 1 − 2

−p(|x|)

x /∈ L ⇒ P [M(x) = 0] ≥ 1 − 2

−p(|x|)

В следующей лемме, мы используем следующие результаты из теории вероятностей:

Теорема 9 Закон Больших Чисел Бернулли Пусть событие A может произойти в любом из t независимых

испытаний с одной и той же вероятностью p, и пусть M

— число осуществлений события A в t испытаниях.

Тогда

7−→ p, причем, для любого ε > 0:





− p



≥ ε



≤

p(1 − p)

tε

Теорема 10 Оценка Чернова (Chernoﬀ bounds). Пусть M

, . . . , M

— независимые события, каждое из ко-

торых имеет вероятность p ≥

. Тогда вероятность одновременного выполнения более половины событий

будет больше, чем 1 − exp(−2(p −

)

t).

Лемма 11 BPP

weak

= BPP

Доказательство Очевидно, что BPP ⊆ BPP

weak

, для этого достаточно положить f(x) ≡

и p(|x|) ≡ 6.

Теперь покажем BPP

weak

⊆ BPP. Пусть L ∈ BPP

weak

, обозначим через M

weak

ВМТ из определения 28, построим

M из определения 27 «BPP».

На входе x, машина M, вычислит p(|x|) и f (|x|), и будет запускать t = 6p

(|x|) раз машину M

weak

, (обозначим

результат i-го запуска через M

weak

и возвращать «1» если M

i=1

weak

> t · f(|x|), или «0» в противном случае.

Рассмотрим вероятность ошибки первого рода P

err

= P (M(x) = 0|x ∈ L):

err

= P (M

< t · f(|x|))

Заметим, что при x ∈ L, матожидание «суммарного голосования» машин M

weak

будет:

E(M

(x)) = t · E



weak

(x)



≥ t · (f(|x|) +

p(|x|)

откуда, применяя теорему 9, и учитывая, что 0 ≤

E(M

)

≤ 1, получаем:

err

≤ P





−

E(M

)



≥

p(|x|)



≤

(|x|)

≤

Вероятность ошибки второго рода P

err

= P (M(x) = 1|x /∈ L) оценивается аналогично. 2

Лемма 12 BPP

strong

= BPP

Доказательство Очевидно, что BPP

strong

⊆ BPP, осталось показать обратное вложение. Действуем аналогично

лемме 11, строим машину M

strong

, запуская t = 2p(|x|) + 1 раз (пусть будет нечетное число) обычную BPP-машину

M, и принимая решения на основе «большинства» ее результатов. Если x ∈ L, то, согласно теореме 10, вероятность

правильного ответа:

P (M

strong

(x) = 1) ≥ 1 − exp

−2



p −



· t

= 1 − exp

−2



−



· (2p(|x|) + 1)

= 1 − exp



−

2p(|x|) + 1



> 1 − exp



−

p(|x|)



> 1 − 2

−p(|x|)

1.4.3 Класс PP.

Теперь познакомимся с максимально широким классом языков, распознаваемых полиномиальной ВМТ.

Определение 30 Класс сложности PP (Probability Polynomial-time) состоит из всех языков L для которых

существует полиномиальная ВМТ M, такая что:

x ∈ L ⇒ P [M(x) = 1] >

x /∈ L ⇒ P [M(x) = 0] >

По опыту разделов 1.4.1 и 1.4.2, читатель может предположить, что константа «

» также выбрана произвольно,

«для красоты», но здесь это не так. В отличии от определений 20 «RP», 27 «BPP», в определении 30 «PP», мы

не никак не можем заменить константу «

» на любую большую константу, т.к. в этом случае, нет гарантированной

возможности амплификации вероятности за полиномиальное время.

Обратите внимание, что в определении 30 «PP», важна даже строгость неравенства (что необязательно для опре-

делений 20 «RP», 27 «BPP»), т.е. нельзя заменить символы «>» на «≥», т.к. тогда определение полностью «выродит-

ся», ведь проверяющую машину можно будет заменить подбрасыванием одной монетки. Единственное ослабление, на

которое мы можем пойти — пожертвовать строгостью одного из неравенств, в определении.

Определение 31 Класс сложности PP

weak

состоит из всех языков L для которых существует полиномиаль-

ная ВМТ M, такая что:

x ∈ L ⇒ P [M(x) = 1] >

x /∈ L ⇒ P [M(x) = 0] ≥

Упражнение 23 Что будет, если в определении 31, в обоих неравенствах поставить «≥»? Какой класс языков

будет определен?

Лемма 13 PP

weak

= PP

Доказательство Очевидно, доказывать нужно только вложение PP ⊆ PP

weak

, для чего мы покажем, как для любого

языка L ∈ PP

weak

, из машины M

weak

(машина M из определения 31) сделать машину M из определения 30 «PP».

Пусть машина M

weak

использует не больше w(|x|) случайных бит (см. определение 19 «oﬄine ВМТ»), машина M будет

использовать p(|x|) = 2 · w(|x|) + 1 случайных бит следующим образом:

M(x, hr

, . . . , r

p(|x|)

i) ≡ (r

w(|x|)+1

∨ . . . ∨ r

p(|x|)

) ∧ M

weak

(x, hr

, . . . , r

w(|x|)

i),

причем, «оптимизируя» вычисление этого выражения, мы даже не будем запускать M

weak

, если

w(|x|)+1

∨ . . . ∨ r

p(|x|)

= 0, что, очевидно, может произойти с вероятностью 2

−(w(|x|)+1)

Итак, рассмотрим случай x ∈ L. Тогда P (M

weak

(x) = 1) >

, причем P (M

weak

(x) = 1) ≥

+ 2

−w(|x|)

, т.к. всего

вероятностных строк не больше 2

w(|x|)

, и минимальный «квант» вероятности, соответствующий одной вероятностной

строке будет не меньше 2

−w(|x|)

P (M(x) = 1) ≥



1 − 2

−(w(|x|)+1)



· P (M

weak

(x) = 1)

≥



1 − 2

−(w(|x|)+1)





+ 2

−w(|x|)



≥

+ 2

−(w(|x|)+1)



− 2

−w(|x|)



Если x /∈ L, то P (M

weak

(x) = 0) ≥

, а

P (M(x) = 0) ≥



1 − 2

−(w(|x|)+1)



· P (M

weak

(x) = 0) + 2

−(w(|x|)+1)

≥



1 − 2

−(w(|x|)+1)



+ 2

−(w(|x|)+1)

Исследуем отношение класса PP к известным нам классам сложности.

Лемма 14 PP ⊆ PSPACE

Доказательство Для любого языка L ∈ PP, из машины M

(машина M из определения 30 «PP») можно сделать

машину M, которая последовательно запускает M

на x и всех 2

p(|x|)

возможных вероятностных строках, и резуль-

тат определяется по большинству результатов запусков. Машина M будет разрешать язык L, и потреблять не более

полинома ячеек на ленте, т.к. каждый запуск M

может использовать один и тот же полиномиальный отрезок ленты.2

Лемма 15 NP ⊆ PP

Доказательство Покажем, как для любого языка L ∈ NP, из машины M

(машина M из определения 15) сделать

машину M из определения 31. Пусть размер подсказки y для машины M

ограничен полиномом p(|x|). Тогда машина

M будет использовать p(|x|) + 1 случайных бит следующим образом:

M(x, hr

, . . . , r

p(|x|)+1

i) ≡ r

p(|x|)+1

∨ M

(x, hr

, . . . , r

p(|x|)

При x ∈ L, P (M(x) = 1) =

+ 2

−p(|x|)

. При x /∈ L, P (M(x) = 0) =

. Таким образом, учитывая лемму 13,

получаем L ∈ PP

weak

= PP. 2

Аналогично получаем:

Лемма 16 coNP ⊆ PP

1.4.4 Класс ZPP. Вероятностное распознавание без ошибок.

Пока, в разделах 1.4.1, 1.4.2 и 1.4.3 мы рассматривали «ошибающиеся» вероятностные алгоритмы распознавания.

Еще один интересный класс вероятностных алгоримов распознования — алгоритмы, которым, в дополнение к стан-

дартным ответам «0» и «1», разрешено выдавать неопределенный ответ «не знаю», который не считается ошибочным.

Используя эти алгоритмы, мы можем определить еще один класс языков:

Определение 32 Класс сложности ZPP состоит из всех языков L для которых существует полиномиальная

ВМТ M, возвращающая только ответы «0»,«1»,«не знаю», причем:

x ∈ L ⇒ P [M(x) = 1] >

∧ P [M(x) = 1] + P [M(x) = «не знаю»] = 1

x /∈ L ⇒ P [M(x) = 0] >

∧ P [M(x) = 0] + P [M(x) = «не знаю»] = 1

Оказывается, у этого класса есть и альтернативное определение:

Лемма 17 ZPP = RP ∩coRP

Доказательство ZPP ⊆ RP, т.к. для любого языка L ∈ ZPP, из машины M

ZPP

(машина M из определения 32 «ZPP»)

можно сделать машину M из определения 20 «RP»:

Answer = M

ZPP

(x)

if Answer = «не знаю» then

Answer = 0

end if

RETURN Answer

Действительно, если x ∈ L, то P [M

ZPP

(x) = 1] >

и следовательно, P [M(x) = 1] ≥

. Если x /∈ L, то

P [M(x) = 0] = P[M

ZPP

(x) = 0] + P [M

ZPP

(x) = «не знаю»] = 1.

Аналогично доказывается, что ZPP ⊆ coRP.

Теперь покажем, что RP ∩ coRP ⊆ ZPP. Изготовим машину M для распознавания ZPP из машин M

(M из

определения 20 «RP») и M

coRP

(M из определения 21 «coRP»), используя «безошибочные» возможности обоих ма-

шин:

if M

(x) = 1 then

RETURN «1»

end if

if M

coRP

(x) = 0 then

RETURN «0»

end if

RETURN «не знаю»

1.5 Вероятностно проверяемые доказательства

Говоря неформально, система вероятностной проверки доказательств (Probabilistically Checkable Proof System, PCP,

мы будем назвать ее PCP-системой) для некоторого языка, состоит из полиномиальной проверяющей ВМТ, имеющей

специальный доступ к отдельным битам бинарной строки, представляющей доказательство. Предоставлением этой

строки занимается оракул (oracle), понятие, часто используемое в теории сложности, и обозначающее близкое в все-

могущести существо или устройство, способное находить ответы на поставленные ему вопросы. Машины Тьюринга

(детерминированные, недетерминированные, вероятностные) сопрягаются с этим устройством, путем установки от-

дельной ленты, на которых они пишут вопросы к оракулу, и на который они, после перехода в специальное состояние

«обращение к оракулу» за один такт работы получают ответ. Обычно ограничиваются бинарными оракулами, возвра-

щающими один бит, например, оракул может заниматься распознаванием некоторого языка, возвращая «0/1» резуль-

таты проверки принадлежности слова на оракульной ленте.

В данном случае, оракул является хранителем некоторой строки-доказательства π, состоящей из конкатенации

индивидуальных строк-доказательств π

, специфичных для каждого входного слова x, а проверяющая ВМТ, проверяя

слово x, запрашивает у оракула отдельные биты π

, посылая запросы типа «позиция в строке π

». Соответственно,

в конце вычисления, проверяющая ВМТ выносит вердикт о принадлежности слова языку, причем, в результате, она

должна «одобрить» все x ∈ L, и с вероятностью не меньшей

«забраковать» x /∈ L.

Можно представить судебный/следственный процесс над группой подозреваемых, при котором некому

суперкомпьютеру (Большой Брат, Матрица) известна абсолютно все, для каждого подозреваемого «x» в

нем хранится полнейшее досье «π

», а следователь, допрашивая подозреваемого «x» не имеет сил и времени

изучить абсолютно все досье «π

», и задает суперкомпьютеру запросы по его содержимому, например, «где

был x в такое-то время», «знаком ли x c y», и т.п.

Давайте сравним определение PCP-системы с определением класса NP через понятия «доказательства» и «вери-

фикации» (определение 15). Итак,

1. Верификатором для класса NP была ДМТ, а у PCP-системы — ВМТ.

2. Для каждого x, строка доказательства у NP была полиномиального размера, а у PCP-системы, каждая строка

может быть экспоненциального размера

3. В случае NP, верификатор сразу же получает доступ ко всему доказательству, а PCP-система, при любой длине

доказательства, успеет просмотреть часть не больше чем полиномиальной длины. Впрочем, PCP-система мо-

жет вполне «побрезговать» полным доказательством, даже если оно полиномиального размера, ограничившись

просмотром константы битов из доказательства, или вовсе не смотреть на него, вынеся результат из исследо-

вания входного слова и вероятностного «подбрасывания монеток». Также, PCP-система может обойтись и без

«монеток».

Теперь дадим более формальное определение:

Определение 33 Системой вероятностной проверки доказательств (PCP-системой) для языка L, называ-

ется ВМТ M с оракулом, для которой выполняются следующие условия:

1. «completeness» ∀x ∈ L, существует оракул π

, такой что,

P [M

(x) = 1] = 1

2. «soundness» ∀x /∈ L, и для любого оракула π выполняется:

P [M

(x) = 1] ≤

Заметим, что PCP-системы подразделяют на адаптивные и неадаптивные, в зависимости от того, зависят ли

запросы к оракулу от предыдущих его ответов, или система, получив на вход слово x, получает строку случайных битов,

и на основе этой строки и входного слова формулирует все свои запросы к оракулу, и получив на них ответы, больше к

нему не обращается. Понятно, что неадаптивные системы являются частным, и следовательно более слабым случаем

адаптивных систем, и далее, мы по умолчанию, будет считать PCP-системы адаптивными.

Теперь определим, какие ресурсы потребляет PCP-система, и на основе чего вводить специфические меры и классы

сложности. Таких ресурсов будет два (мы исключаем время и память — объявив процесс верификации полиномиаль-

ным, мы более не интересуемся ни тем ни другим): «вероятность» и «ответы оракула».

Итак:

Больше, чем экспоненциального размера она быть не может, т.к. тогда номера позиций в этой строке будут более чем полиномиальны, и поли-

номиальная ВМТ не успеет их даже написать на оракульной ленте, и они окажутся незапрошенными

Определение 34 Пусть r, q : N ⇒ N, неотрицательные целочисленные функции.

Класс сложности PCP(r(·), q(·)) состоит из языков, имеющих верифицирующую PCP-систему, которая на

входе x:

1. потребляет не более r(|x|) случайных бит;

2. делает не более q(|x|) запросов к оракулу.

Для множеств целочисленных функций R, Q, определим

PCP(R, Q) ≡

[

r∈R ,q∈Q

PCP(r(·), q(·))

Т.е. одним определением 34 «PCP», в зависимости от этих двух параметров, определяется множество различных

классов сложности. Например, класс PCP(poly, poly) очень мощный, доказано, что он совпадает с сверхшироким

классом NEXP ≡ NT IME(2

poly

Если рассмотреть вырожденные случаи (когда один из параметров равен нулю), то определение 34 «PCP», пере-

ходит в определение классов NP (см. определение 15 «NP/ДМТ»)

PCP(0, poly) = NP

и coRP (см. определение 23 «co RP/ДМТ»):

PCP(poly, 0) = coRP

Однако, ценность PCP заключается не только в «сведении к единому знаменателю» определений классов coRP и

NP, а в демонстрации связи и взаимозаменяемости «вероятностного» и «информационного» ресурсов. Оказалось, что

один и тот же класс языков может быть определен, как PCP(P, Q) с разными парами (P, Q). Попросту говоря, можно,

обменивать «вероятность» на «запросы к оракулу» и наоборот.

Попробуем увидеть, как это может происходить.

Лемма 18 PCP(log, poly) ⊆ NP

Доказательство Пусть язык L лежит в PCP(log, poly). Покажем, как построить верификатор класса NP, который

сможет разрешить L. Рассмотрим M

—оракульную ВМТ из PCP-системы, распознающей L (можно считать ее адап-

тивной). Введем обозначения:

1. hr

, . . . , r

i — значения в вероятностной строке, подтребляемой ВМТ (см. определение 19 «oﬄine ВМТ»);

2. Для каждой вероятностной строки i, обозначим



, . . . , q



— последовательность вопросов к оракулу, осно-

ванные только на входном слове x и hr

, . . . , r

i, а через

, . . . , π

— ответы оракула на эти вопросы.

Сначала обеспечим «NP-одобрение», т.е. проверим, что для любого входного слова x ∈ L существует полиноми-

альное «NP-доказательство» y, такое, что их вместе (x#y) распознает полиномиальная ДМТ. Мы не можем исполь-

зовать как «NP-доказательство» все доказательство оракула π, или даже оракульное доказательство π

для входного

слова x, т.к. любое из этих доказательств может быть экспоненциального размера, но если мы рассмотрим массив

, . . . , π

, для i ∈ (1, . . . , m), то мы видим, что его можно закодировать строкой y полиномиальной длины, т.к.

число различных вероятностных строк m ≤ 2

log(|x|)

= poly(|x|), число ответов от оракула также не больше poly(|x|),

таким образом y — полиномиальное «NP-доказательство» для входного слова x.

Верификатор-ДМТ M, на входе x#y, просимулирует ВМТ M

на всевозможных значениях строк r, и в процес-

се симуляции M

вместо оракула предоставит M

ответы из «NP-доказательства» y (в зависимости от «выпавшей»

«случайной» строки r). Если для каждой строки r, симулируемая M

одобрит x, то то же сделает и M. Так как мы уже

видели, что строк r — полином от |x|, y — полиномиальная строка, симуляция полиномиальной M

— также полином,

то и описанная ДМТ M также будет полиномиальной.

Теперь рассмотрим случай, что x /∈ L, и убедимся, что ∀y : M(x, y) = 0. Допустим, что ∃y : M(x, y) = 1, для x /∈ L.

Но тогда (см. описание работы машины M), мы можем «превратить» это «NP-доказательство» y обратно в некоторого

оракула π

, для которого P

(x) = 1

= 1, что противоречит условию «soundness» из определения 33 «PCP-

система».

Эта лемма показала, как «упаковывать» вероятностные доказательства PCP-систем, преобразуя их в полиноми-

альные «NP-доказательства». Теперь поинтересуемся обратным вложением — какие есть субполиномиальные функ-

ции q(·), чтобы выполнялось:

NP ⊆ PCP(log, q(·))

Говоря неформально — можем ли мы сэкономить на полной честной проверке полиномиальных доказательств,

заменив ее вероятностной, но более быстрой и «дешевой» проверкой?

Оказалось — да. Соответствующий результат, являющийся, вероятно, величайшим достижением теории сложности

за последние два десятиления, формулируется так:

Теорема 11 NP ⊆ PCP(log, O(1))

Доказательство этой теоремы чрезвычайно сложно, занимает порядка сотни страниц, поэтому мы приводим ее без

доказательства. Зато, комбинируя результат этой теоремы 11 «PCP-theorem» с ранее доказанной нами леммой 18,

получаем новое, нетривиальное определение знакомого нам класса NP :

NP = PCP(log, O(1)) (1.11)

Интересно, что доказаны даже более конкретные определения класса NP через PCP, с указанием не класса функ-

ций, описывающих число запросов к оракулу, а число конкретных бит, которых необходимо запросить у оракула, так

например доказано, что

NP = PCP(log, q = 5), (1.12)

где обозначением q = 5 мы отметили что требуется не просто константа, а конкретное число проверочных битов.

И известно, что таких битов не может быть меньше трех, при гипотезе, что P 6= NP, что мы и докажем в следующей

теореме.

Теорема 12 P = PCP(log, q = 2)

Доказательство Естественно, доказать нужно только что PCP(log, q = 2) ⊆ P . Действуем, аналогично лемме 18,

воспользуемся ее обозначениями для имеющейся ВМТ, вероятностных строк, запросов к оракулу, и ответов от оракула.

Так как, на каждое, i-е, бросание монет hr

, . . . , r

iответов от оракула должно быть всего (не больше чем) два



, π



По схеме верификации машиной M

(см. теорему 8 «SAT ∈ NPC») можно построить 2SAT-формулу φ — КНФ, где

будет m-дизъюнкций, соответствующих вероятностным строкам, где каждая дизьюнкция содержит не больше чем 2

переменные, соответствующие ответам оракула



, π



Тогда вопрос о существовании оракульного доказательства π

для заданного слова x эквивалентен выполнимости

2SAT-формулы φ, а эта задача полиномиально разрешима (см. упражнение 20). 2

1.5.1 PCP и неаппроксимируемость

Введение и исследование понятия PCP-системы помогло в доказательствах неаппроксимируемости некоторых опти-

мизационных задач.

Действительно, многие известные оптимизационные задачи, т.е. задачи, в которых находится оптимальное решение,

стоимость которого должна быть максимальна (или минимальна), принадлежат классу NPC или NP-трудны. Однако,

хотя это означает, что при гипотезе P 6= NP точное решение получить эффективно невозможно, эта принадлежность

ничего не говорит о возможности аппроксимации задачи, т.е. нахождения приближенного решения, которого, возмож-

но, будет достаточно во многих практических случаях.

Определение 35 Алгоритмом с мультипликативной точностью C называется приближенный алгоритм,

который при любых исходных данных находит допустимое решение со значением целевой функции, отли-

чающемся от оптимума не более, чем в C раз. Также, для краткости, будем называть такой алгоритм C-

приближенным.

Определение 35 включает все виды приближенных алгоритмов с гарантированной оценкой точности, как алгоритмы

с константной точностью, так и более частный случай алгоритмов, у которых точность C выступает в роли одного из

параметров, и они способны добиться любой заданной точности, расплатившись за нее временем. Разумеется, нас

будут интересовать в первую очередь эффективные, т.е. полиномиальные приближенные алгоритмы.

Обратите внимание — если алгоритм «старается» найти хорошее решение, но не гарантирует точности на всех

входных данных, то его обычно называют эвристикой. В нашем курсе мы не рассматриваем такие алгоритмы, хотя

такие алгоритмы бывают популярными. Как правило, популярность таких эвристик означает, что на большой доле

входных данных они работают хорошо, и значит, можно доказать их положительные характеристики в среднем.

Далее, в этом разделе мы будем рассматривать задачу 10 «3SAT» и ее оптимизационную версию — задачу 13 «MAX-

3SAT»

Задача 13 MAX-3SAT Частный случай задачи 25 «MAXSAT», в которой в каждой скобке-дизъюнкции не бо-

лее трех переменных.

Оказалось, тесно взаимосвязанны следующие вопросы:

• Для любого ли ε > 0 существует

1−ε

–приближенный полиномиальный алгоритм для задачи 13 «MAX-3SAT»?

• Можно ли, при построении PCP-системы для задачи 13 «MAX-3SAT», вероятностно выбирать одну дизъюнк-

цию, проверять с помощью оракула ее выполнимость, и в случае, когда она выполнена, чтобы вероятность невы-

полнимости всей формулы уменьшилась на константу?

Размышляя над этими вопросами, сразу представляем два типа невыполнимых 3SAT-формул:

• «Честные», такие, что при своей невыполнимости у них, при любом выборе значений переменных, невыполни-

мыми оказываются сразу некоторая константная (скажем ε) часть дизъюнкций, и соответственно, вероятностная

проверка любой выбранной дизъюнкции имеет константную вероятность выявить невыполнимую дизъюнкцию,

и «забраковать» всю формулу. Также, заметим, что для таких формул, алгоритм, распознающий существование

1−ε

-приближенного решения, будет собственно, разрешающим алгоритмом.

• «Хитрые», в которых, например, при любом присваивании, невыполнимой оказывается только одна дизъюнкция,

и ее нельзя поймать с константной вероятностью, проверяя по одиночке случайно выбранные дизъюнкции.

Оказалось, есть путь вывести «хитрецов» на чистую воду. Это так называемые усиливающие сводимости

, пред-

ставляющие собой сводимости по Карпу (см. определение 16) к «честным» 3SAT-задачам.

Определение 36 Усиливающая сводимость (amplifying reduction) по сведению произвольного языка L ∈

NP к языку 3SAT (∈ NPC), для заданной константы 1 > ε > 0, есть полиномиально вычислимая функция

φ = f(x), преобразующая входное слово x в экземпляр (формулу φ) задачи 3SAT для которой:

x ∈ L ⇐⇒ φ ∈ 3SAT,

x /∈ L ⇐⇒ φ /∈ 3SAT,

причем, если φ /∈ 3SAT , то доля невыполненных (ложных) дизъюнкций будет не меньше ε.

Видно, если усиливающие сводимости существуют, то их можно использовать для построения эффективных (осо-

бенно по запросам к оракулу) PCP-систем.

Оказывается, да, такие сводимости существуют.

Теорема 13

NP ⊆ PCP(log, O(1)) ⇐⇒ Есть усиливающая сводимость для 3SAT (3SAT → 3SAT ).

Доказательство

⇒: Рассмотрим L ∈ NP, нам дано, что для него существует PCP(log, O(1))-система, покажем же существование

усиливающей сводимости L → 3SAT . Будем использовать обозначения (ВМТ, вероятностные строки, запросы/ответы

оракула), как при доказательстве леммы

18 и теоремы 12.

Для каждого входного слова x (мы не показываем в индексах x, но неявно подразумеваем):

• полиномиальный (от длины входа, 2

O(log(|x|))

) набор всех случайных строк hr

, . . . , r

• Для каждой вероятностной строки r

, запишем ответы оракула на возникшие у проверяющей ВМТ вопросы:



, . . . , π



Далее, действуем как в теореме 12, строим, по «логам» работы ВМТ-верификатора, формулу ψ

, выражающую его

решение на i-том вероятностном наборе hr

, . . . , r

i и зависящую от t переменных



, . . . , π



. Как построить такую

формулу, причем за полиномиальное время, мы уже видели в теореме 8 «SAT ∈ NPC», здесь же построим ее через

построение таблицы истинности (она будет полиномиального размера) и построении КНФ по этой таблице — тогда мы

еще получим, что в ней не больше чем 2

различных дизьюнкций.

Пока еще нет устоявшегося русского перевода

После чего (т.к. дизъюнкции в формуле у нас еще могут содержать до t-переменных) преобразуем, полученную

КНФ ψ

в 3-КНФ φ

, также, как при доказательстве NP-полноты задачи 10 «3SAT». При этом, т.к. каждая t-дизъюнкция

выражается с помощью введения дополнительных переменных, конъюнкцией не более чем t дизъюнкций, не более

чем от трех переменных (назовем их 3-дизьюнкциями), получаем, что φ

содержит не более чем t · 2

3-дизьюнкций.

Выполняя конъюнкцию над всеми φ

, получаем 3КНФ формулу, которую мы построили за полиномиальное время

(напоминаем, что t-константа, и следовательно t · 2

— тоже константа):

φ ≡ ∧

i=1

Осталось убедиться, что описанное преобразование x → φ — действительно усиливающая сводимость.

Пусть x ∈ L, тогда есть оракул π, ответы



, . . . , π



гарантированно убедят проверяющую ВМТ (при любой слу-

чайной последовательности hr

, . . . , r

i) и эти ответы (+значения вспомогательных переменных) будут выполняющим

набором для φ, т.е. φ ∈ 3SAT .

Если же x /∈ L, тогда для любого оракула π не меньше чем в половине исходов r

проверяющая машина M «бракует»

x, и следовательно, должно быть невыполнимо не менее половины φ

. Итак, общее число дизъюнкций в φ не больше

m · t · 2

, а число невыполненных дизьюнкций никак не меньше

, что не меньше доли ε =

2·t·2

⇐: Теперь у нас есть ε-усиливающая сводимость f : 3SAT → 3SAT , покажем, что выполняется условие теоре-

мы 11 «PCP-theorem». Рассмотрим любой L ∈ NP C, например 3SAT , и построим для него требуемую PCP-систему.

Для входного слова — формулы φ — проверяющая ВМТ M будет работать следующим образом:

1. φ

= f(φ)

2. случайно-равномерно выбираем d

e дизъюнкций для проверки. (|r| = O(log(|φ

|)) = O(log(|φ|))).

3. Задаем не более d

e вопросов оракулу, о том, какие значения нужно бы присвоить для выполнимости, встретив-

шимся в этих дизъюнкциях переменным.

4. Получив ответы, вычисляем коньюнкцию из выбранных дизъюнкций, бракуем ее, если она равна 0, и принимаем,

если равна 1.

Проанализируем алгоритм M:

• Если формула выполнима, подходящий оракул покажет нам выполнимость любых выбранных нами дизъюнкций

и мы ее не забракуем — «completeness» условие выполнено.

• Если формула невыполнима, то вероятность того, что мы d

eраз не угадаем ни одну невыполненную дизъюнкцию,

будет не больше

(1 − ε)

≤

Т.е. выполнено и «soundness»-условие.

Из теоремы 13 и теоремы 11 «PCP-theorem» немедленно следует существование усиливающей сводимости для

задачи 3SAT, откуда следует важное утверждение о сложности аппроксимации (попросту говоря — неаппроксимируе-

мости) задачи 13 «MAX-3SAT»:

Теорема 14 Задача 13 «MAX-3SAT» NP-трудна.

Доказательство Покажем, что задача 13 «MAX-3SAT», даже в форме задачи на разрешение: «правда ли, что есть

присваивание, при котором данная 3КНФ-формула φ имеет долю невыполненных конъюнкций не более ε?» NP-трудна.

Возьмем любую φ, входную для 3SAT , (3SAT ∈ NPC) и с помощью ε-усиливающей сводимости сведем ее к φ

. Решив

задачу 13 «MAX-3SAT» для ε из нашей сводимости, мы ответим на вопрос φ

∈ 3SAT .

Таким образом, для задачи 3SAT доказано, что апроксимация ее с произвольным ε не менее трудная задача, чем

ее точное решение. Обратите внимание: «с произвольным ε»! Действительно, для некоторых ε, задачу 3SAT удалось

решить эффективно, т.е. полиномиально. Точнее, найден полиномиальный алгоритм для 3SAT аппроксимации с ε =

и доказано, что эта оценка — точная, т.е. апроксимация 3SAT с точностью ε <

есть NP-трудная задача.

NOTAND

NOT

AND

Рис. 1.9: Схема сравнения двух битовых строк

1.6 Схемы и схемная сложность

Этот раздел основан на соответствующей главе [А. 99].

Схема (булева) — это способ вычислить функцию f : {0, 1}

→ {0, 1}

Помимо исходных переменных x

, . . . , x

, для которых вычисляется значение f, схема использует некоторое коли-

чество вспомогательных переменных y

, . . . , y

и некоторый набор (базис) булевых функций F.

Схема S в базисе F определяется последовательностью присваиваний Y

, . . . , Y

Каждое присваивание Y

имеет вид

:= f

, . . . , u

где f

(·) ∈ F, а переменная u

(1 ≤ p ≤ r) — это либо одна из исходных переменных x

(1 ≤ t ≤ n), либо вспомога-

тельная переменная y

с меньшим номером (1 ≤ l < i).

Таким образом, для каждого набора значений исходных переменных последовательное выполнение присваиваний,

входящих в схему, однозначно определяет значения всех вспомогательных переменных. Результатом вычисления

считаются значения последних m переменных y

s−m+1

, . . . , y

Схема вычисляет функцию f, если для любых значений x

, . . . , x

результат вычисления — f(x

, . . . , x

Определение 37 Схема называется формулой, если каждая вспомогательная переменная используется в

правой части присваиваний только один раз.

Обычные математические формулы именно так задают последовательность присваиваний: «внутри» формул не

принято использовать ссылки на их части или другие формулы.

Схему можно также представлять в виде ориентированного ациклического (См. Рис.1.9) графа, у которого верши-

ны входной степени 0 (входы) помечены исходными переменными; остальные вершины (функциональные элементы)

помечены функциями из базиса; ребра помечены числами, указывающими номера аргументов; вершины выходной сте-

пени 0 (выходы) помечены переменными, описывающими результат работы схемы.

Вычисление на графе определяется индуктивно: как только известны значения всех вершин y

, . . . , y

, из которых

ведут ребра в данную вершину v, вершина v получает значение y

= f

, . . . , y

), где f

— базисная функция,

которой помечена вершина.

При переходе к графу схемы мы опускаем несущественные присваивания, которые ни разу не используются на

пути к выходным вершинам, так что они никак не влияют на результат вычисления.

Определение 38 Базис называется полным, если для любой булевой функции f есть схема в этом базисе,

вычисляющая f.

Ясно, что в полном базисе можно вычислить произвольную функцию

f : {0, 1}

→ {0, 1}

(такую функцию можно представить как упорядоченный набор из m булевых функций).

Булева функция может быть задана таблицей значений. Приведем таблицы значений для трех функций

NOT (x) = ¬x, OR(x

, x

) = x

∨ x

, AN D(x

, x

) = x

∧ x