Кузюрин Н.Н. Фомин С.А. Сложность комбинаторных алгоритмов. Курс лекций

Подождите немного. Документ загружается.

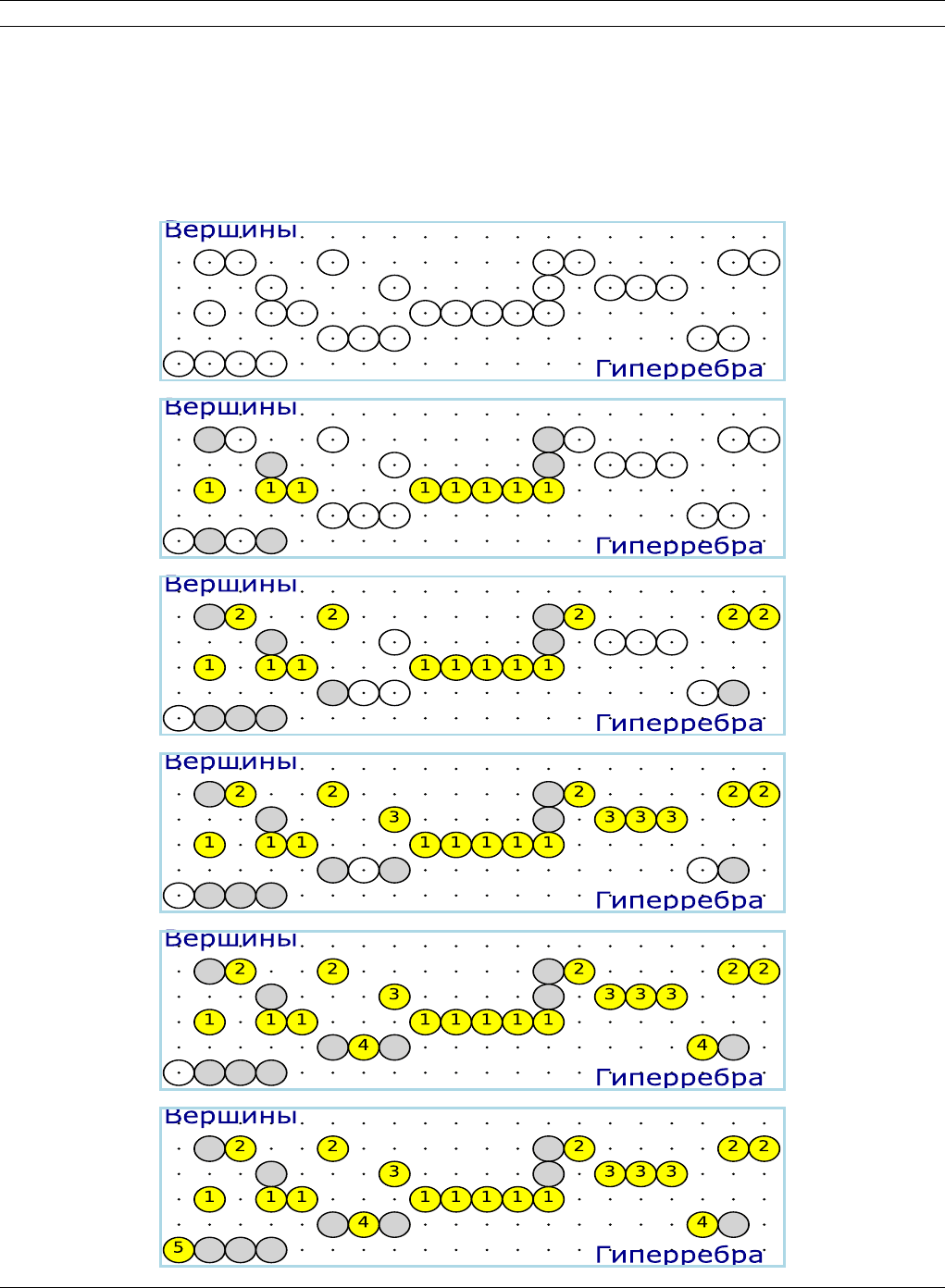
Алгоритм 18 Жадный алгоритм для задачи 20 «MSSC»

Вершины нумеруются последовательно, причем на каждом шаге выбирается вершина, покрывающая наибольшее чис-

ло непокрытых ребер, покрытые ею ребра отмечаются покрытыми и получают f(e) = f(v), и процесс повторяется,

пока вершины не закончатся.

Ниже представлена иллюстрация работы алгоритма — гиперграф представлен матрицей инцидентности, строки со-

ответствуют вершинам, столбцы — гиперребрам. Непокрытые пары (вершина,ребро) представлены белыми круга-

ми, «обработанные» вершины получают последовательный номер, который присваивается обрабатываемой вершине

(f(v)), и всем непокрытым ребрам, покрываемым данной вершиной (f (e)). Серыми кругами обозначаются пары (v,e),

для тех ребер e, для которых f(v) > f(e) (т.е. которые были покрыты ранее, чем «дошла очередь» до v).

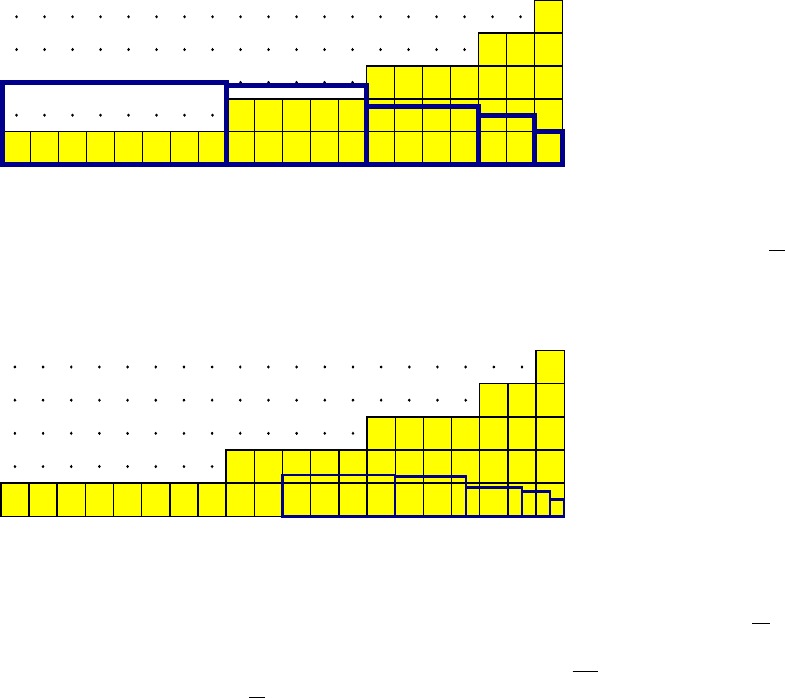
Мы хотим показать, что площадь второй гистограммы не более, чем в четыре раза превосходит площадь первой

гистограммы. Для доказательства этого факта уменьшим гистограмму e → p

в 4 раза следующим образом.

Уменьшим высоту каждого столбца в два раза. Тогда высота столбца, соответствующего ребру e, станет равной

Уменьшим также в два раза ширину каждого столбца. Таким образом, ширина новой гистограммы будет равна |E|/2.

Сдвинем эту новую гистограмму вправо так, что она займет площадь занимаемую ранее столбцами с |E|/2 + 1 до |E|

(для простоты полагаем, что |E| — четно).

Теперь покажем, что при указанном размещении уменьшенной второй гистограммы, она целиком помещается в

первой гистограмме.

Рассмотрим произвольную точку-гиперребро e на гистограмме e → p

, и пусть k обозначает номер шага (и вер-

шину), на котором алгоритм 18 «Greedy MSSC» покрыл ребро e. Тогда высота выбранного столбца равна p

, а

расстояние от e до правой границы не превосходит r

Преобразование переводит точку e в новую точку e

. Высота h столбца e

будет h =

, и расстояние r от e

до правой границы будет удовлетворять условию r ≤

. Мы покажем теперь, что столбец e

должен лежать внутри

гистограммы e → f

∗

(e).

Для того, чтобы стобец e

лежал внутри первой гистограммы e → f

∗

(e), достаточно показать, что к шагу h (округ-

ленному вниз до ближайшего целого) по крайней мере r ребер (округление вверх до ближайшего целого) все еще не

покрыты оптимальным алгоритмом.

Рассмотрим теперь только ребра из множества R

. Ни одна вершина не может покрыть более x

ребер из R

(по

свойству алгоритма Greedy). Следовательно, за bhc шагов оптимальный алгоритм может покрыть не более bhcx

≤

/2c ребер из R

, оставляя, тем самым, непокрытыми не менее d|R

|/2e ≥ dre ребер из R

. Это означает, что точка

лежит внутри первой гистограммы. 2

Упражнение 41 Приведите пример гиперграфа, для которого алгоритм 18 «Greedy MSSC» будет добавлять

вершины с нарушением монотонного убывания p

Упражнение 42 Пусть для гиперграфа H = (V, E), где V = {1, 2, . . . , |V |}, множество вершин {1, 2, . . . , t} об-

разуют минимальное по мощности покрытие всех ребер гиперграфа.

Приведите пример гиперграфа, в котором в оптимальном решении задачи покрытия с минимальной сум-

мой начальный отрезок длины t не совпадает с {1, 2, . . . , t}.

2.1.3 Жадный алгоритм для задачи о рюкзаке

Рассмотрим следующую задачу

Задача 21 0-1 РЮКЗАК (Knapsack) Даны натуральные числа a

, . . . , a

(называемые размерами или весами

предметов), c

, . . . , c

(стоимости предметов) и B (размер рюкзака).

Найти максимальное значение f

∗

целевой функции

f ≡

i=1

→ max

с ограничением на размер «рюкзака»

i=1

≤ B, x

∈ {0, 1}.

Содержательно задача означает выбор предметов с наибольшей суммарной стоимостью, умещающихся в рюк-

зак заданного размера. Эта задача часто возникает при выборе оптимального управления в различных экономико-

финансовых областях (распределение бюджета отдела по проектам и т.п.).

Рассмотрим, какого результата можно добиться, используя, как в разделе 2.1.1, «жадный подход».

Первая идея, которая обычно возникает при знакомстве с этой задачей, это выбирать предметы по убыванию их

относительной стоимости, помещая в рюкзак все, что помещается, или, более формально:

1. Упорядочим по убыванию элементы массива

, . . . ,

2. В соответствии с этим упорядочиванием полагаем переменные x

равными 1, если установка x

= 1 не приводит

к нарушению ограничения

i=1

≤ B.

К сожалению, о качестве такой эвристики ничего утверждать нельзя — для любого числа k, можно представить

входной набор данных, для которых алгоритм выберет набор хуже в k раз оптимального набора. Понятно, что пробле-

ма состоит в том, что «польстившись» на первый небольшой, но «относительно дорогой» предмет, алгоритм рискует

пропустить большой и ценный предмет из оптимального набора.

Оказывается, гарантированное качество работы этой эвристики можно улучшить, если, после окончания ее работы,

сравнить стоимость полученного допустимого решения с максимальным коэффициентом c

max

, и в соответствии с мак-

симумом, выбрать либо «жадное решение», или один предмет с максимальной стоимостью (мы считаем, что размеры

всех предметов не превосходят размер рюкзака — в противном случае их просто можно исключить из рассмотрения).

Получится так называемый модифицированный жадный алгоритм, (см. алгоритм 19 «Рюкзак-Жадный»), дающий

приближенное допустимое решение, которое мы обозначим через x

, а значение целевой функции для него — через

. Нетрудно доказать, что выполнены следующие неравенства:

Упражнение 43 Для значения решения f

полученного модифицированным жадным алгоритмом 19 «Рюк-

зак-Жадный» для задачи о рюкзаке, и оптимального значения f

∗

выполняется

∗

/2 ≤ f

≤ f

∗

. (2.5)

2.1.4 Алгоритм Кристофидеса для метрической задачи коммивояжера

Напомним некоторые определения.

Определение 46 Эйлеровым путем в графе называется произвольный путь, проходящий через каждое реб-

ро графа в точности один раз.

Определение 47 Замкнутый эйлеров путь называется эйлеровым обходом или эйлеровым циклом.

Определение 48 Эйлеров граф — граф, в котором существует эйлеров обход.

Приведем критерий эйлеровости графа.

Теорема 20 Эйлеров обход в графе существует тогда и только тогда, когда граф связный и все его вершины

четной степени.

Доказательство Доказательство достаточности условия теоремы будет следствием анализа алгоритма нахождения

эйлерова пути (алгоритм 20 «Цикл Эйлера»).

Необходимость условия очевидна, так как если некоторая вершина v появляется в эйлеровом обходе k раз, то это

означает, что степень этой вершины в графе составляет 2k. 2

Нахождение эйлерова цикла можно выполнить эффективно, с помощью алгоритма 20 «Цикл Эйлера», основная

идея которого содержится в построении произвольных замкнутых циклов (если вы окажетесь в эйлеровом графе, и

будете идти произвольно по его ребрам, сжигая их после своего прохода, то рано или поздно вы вернетесь в точку

старта), и обьединении таких циклов в единый эйлеров цикл.

Лемма 20 Сложность алгоритма 20 «Цикл Эйлера» есть O(|E|).

Доказательство Сумма времени выполнения всех вызовов процедуры «euler» будет O(|E|), т.к. каждое обработан-

ное ребро удаляется из графа. Объединение циклов в данной реализации квадратично, но можно также реализовать

за O(|E|), если дополнительно поддерживать хэш-таблицу, указывающую на вершины, к которым можно присоединять

дополнительные циклы. 2

Алгоритм 19 Модифицированный жадный алгоритм для задачи 0-1 РЮКЗАК

Жадный алгоритм для задачи о рюкзаке.

def knapsack_greedy (A, B, C):

print , A, , B, , C

T ← {}

for i ∈ xrange (len (A)) :

T [ﬂoat (A[i])/ﬂoat (C[i])] ← i

Сортируем ключи - "удельную привлекательность по убыванию

K ← T.keys (); K.sort ()

print , K

Набиваем рюкзак до наполнения, предметами в порядке их полезности.

← 0; ← 0;

for i ∈ K :

if + A[T [i]] ≤ B :

← + A[T [i]]

print , C[T[i]], , A[T [i]],

← + C[T [i]]

← max (C)

print , , ,

← max ( , )

print ,

return

Алгоритм 20 Алгоритм нахождения Эйлерова цикла

def euler_circuit (G):

← [ ] # Эйлеров цикл - массив вершин.

возвращает локальный замкнутый цикл

def euler (v) :

← {}

while (G.degree (v) > 0) : # пока не оказались в "безвыходной" вершине

w ← G.neighbors (v)[0] # берем w — первого попавшегося "соседа" v

[v] ← w # записываем ребро (v, w) в cycle и стираем его из графа

G.delete_edge (v, w)

v ← w # повторяем все с вершиной w

return

добавляет цикл к эйлерову пути

def add_cycle () :

print , ,

if len ( ) > 0: # ищем вершину, к которой можно добавить цикл

for i ∈ xrange (len ( )):

if G.degree ( [i]) > 0:

v ← [i]

break

else: # Подготавливаем пока пустой EP к присоединению цикла

v ← G.nodes ()[0] # выбираем первую попавшуюся вершину

.append (v) # и добавляем ее в EP

i ← 0

c ← euler (v)

print c, ,

while c: # пока не перенесли все содержимое цикла

i ← i + 1; .insert (i, c[v]) # вставляем очередную вершину в EP

w ← c[v] # переходим к следующей

del c[v] # удаляя из цикла вставленную.

v ← w

Проверка, необходимых и достаточных условий существования

for v ∈ G.nodes ():

if (G.degree (v) % 2) 6= 0: print ; return

while (G.number_of_edges () > 0):

add_cycle () # добавляем цикл к эйлерову пути

return

Определение 49 Задача КОММИВОЯЖЕР (Задача 3 «TSP») называется метрической, если для матрицы

расстояний выполнено неравенство треугольника:

∀i, j, k d

≤ d

+ d

Заметим, что здесь рассматривается полный граф.

Необходимо отметить, что метрическая задача коммивояжера NP-полна. Это легко доказать, заметив что если

веса ребер полного графа принимают только два значения 1 и 2, то задача является метрической. В свою очередь,

построение минимального обхода здесь эквивалентно ответу на вопрос: существует ли в графе с вершинами исходного

графа и ребрами, имеющими вес 1, гамильтонов цикл?

Для этой вариации задачи можно предложить следующий приближенный алгоритм 21 «Метрическая TSP» с муль-

типликативной точностью 2.

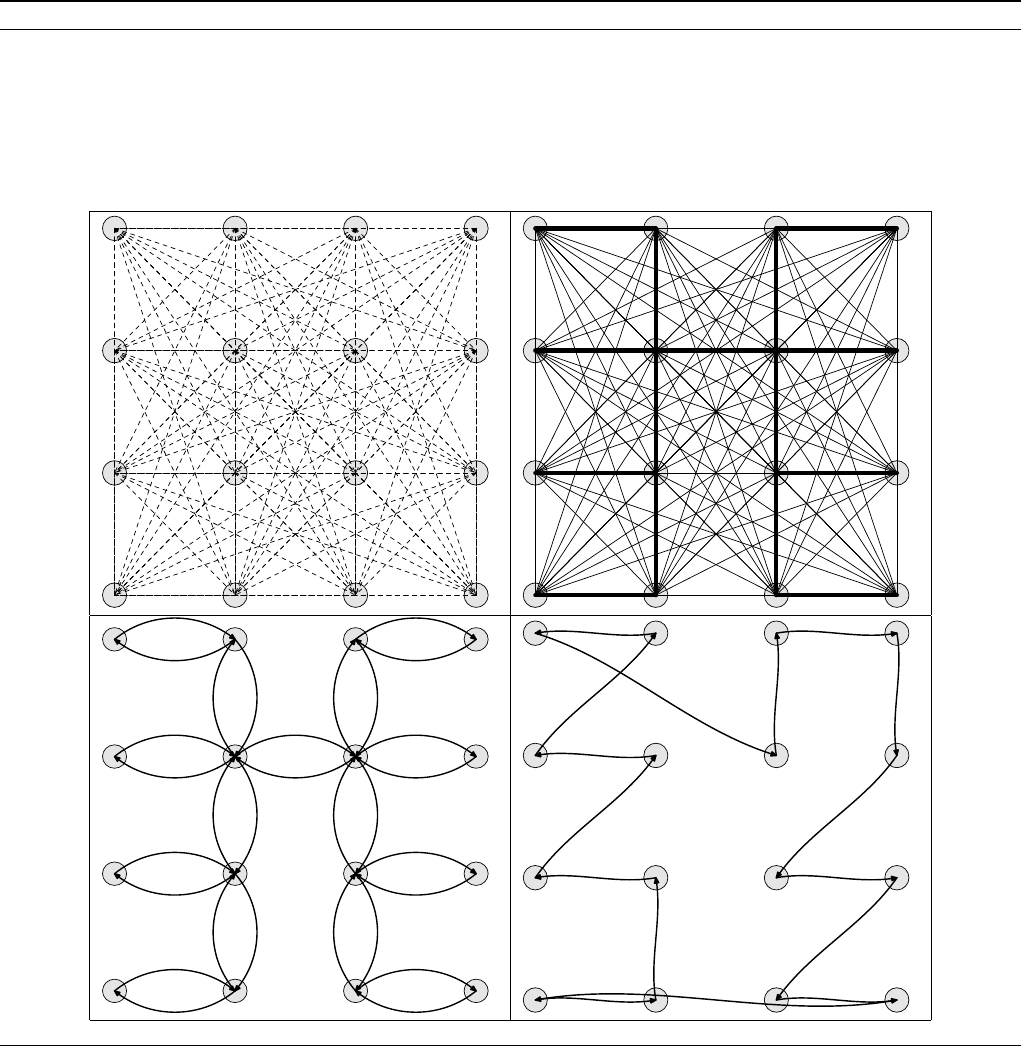
Алгоритм 21 Простой алгоритм для решения метрической задачи коммивояжера

1. Найти минимальное остовное дерево T с матрицей весов [d

] (пунктиром обозначены ребра не вошедшие в ми-

нимальное остовное дерево).

2. Построить эйлеров граф G и эйлеров обход в G, продублировав все ребра дерева T

3. Из эйлерова маршрута (обхода) гамильтонов цикл строится путем последовательного вычеркивания вершин,

встретившихся ранее.

Пример. В рассмотренном на рисунке примере эйлеров цикл составляет следующий маршрут:

→ v

Соответствующий ему вложенный тур (гамильтонов цикл) таков:

, v

Теорема 21 Отношение длины пути, построенного алгоритмом 21 «Метрическая TSP» к длине оптималь-

ного пути, не превосходит 2.

Доказательство Длина кратчайшего гамильтонова пути не меньше длины кратчайшего остовного дерева. Длина эй-

лерова маршрута в G равна удвоенной длине минимального остовного дерева (по построению). По неравенству тре-

угольника, полученный гамильтонов цикл имеет длину не превосходящую длину эйлерова обхода, т.е. удвоенную длину

минимального остовного дерева.

Это и означает, что длина найденного гамильтонова цикла превосходит длину кратчайшего гамильтонова цикла не

более, чем в два раза. 2

Однако, лучшим по точности полиномиальным приближенным алгоритмом для метрической задачи коммивояжера

остается алгоритм Кристофидеса (алгоритм 22 «Кристофидес-TSP»), предложенный им в 1976 г.

Сначала пара определений.

Определение 50 Паросочетание — подмножество ребер графа, такое что никакие два ребра из этого

подмножества не инцидентны какой-либо одной вершине.

Определение 51 Совершенное паросочетание — паросочетание, покрывающее все вершины графа.

Отметим, что алгоритм 22 «Кристофидес-TSP» является полиномиальным алгоритмом. Шаг 1 может выполнен за

время O(n), шаг 2 — за время O(n

). Шаги 3–5 выполняются за линейное время.

Теорема 22 Отношение длины пути, построенного алгоритмом 22 «Кристофидес-TSP» к длине оптималь-

ного пути, не превосходит 3/2.

Доказательство Во-первых, отметим, что построенный граф G

действительно эйлеров (согласно теореме 20), т.к.

каждая вершина, которая имеет четную степень до добавления ребер паросочетания T , имеет ту же степень, а степень

каждой вершины нечетной степени — увеличивается на единицу (из-за добавления ребра паросочетания). Кроме того,

граф связен, т.к. содержит остовное дерево.

Длина результирующего гамильтонова цикла P

удовлетворяет неравенству:

c(P

) ≤ c(P

) = c(G

) = c(T ) + c(M ).

С другой стороны, для кратчайшего гамильтонова цикла P

∗

выполнено:

c(T ) ≤ c(P

∗

) ≤ c(P

Пусть i

, i

, ...,i

— множество вершин нечетной степени в T , в том порядке каком они появляются в P

∗

. Рас-

смотрим два паросочетания на этих вершинах:

= {i

, i

}, {i

, i

}, . . . , {i

2m−1

, i

}

= {i

, i

}, {i

, i

}, . . . , {i

, i

Из неравенства треугольника (докажите это в качестве упражнения)

c(P

∗

) ≥ c(M

) + c(M

Но, M — кратчайшее паросочетание, значит c(M

) ≥ c(M), c(M

) ≥ c(M). Имеем:

c(P

∗

) ≥ 2c(M) ⇒ c(M ) ≤

c(P

∗

Окончательно имеем

c(P

) ≤ c(T ) + c(M ) ≤ c(P

∗

) +

c(P

∗

) =

c(P

∗

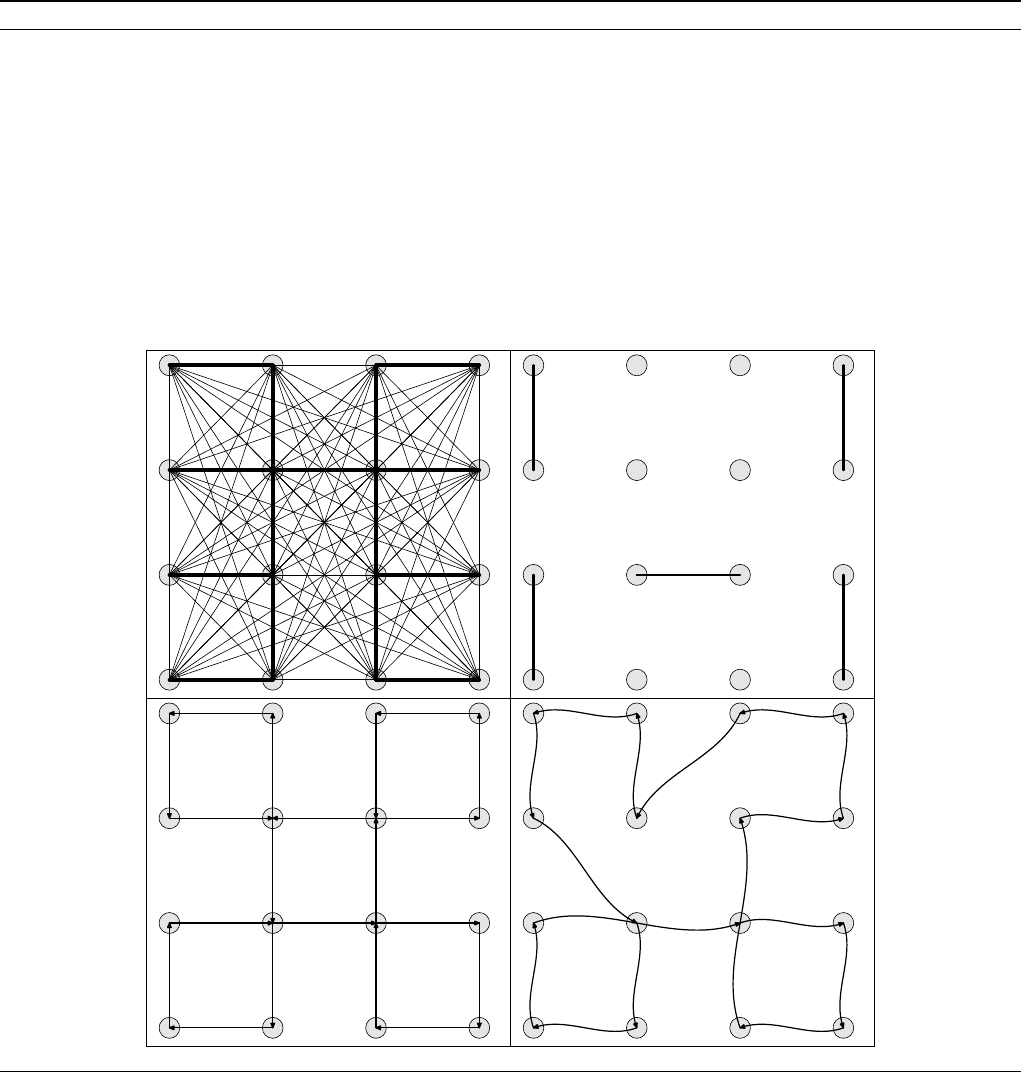
Алгоритм 22 Алгоритм Кристофидеса для решения метрической TSP

Вход: m × n матрица [d

j] для графа G — постановка задачи 3 «TSP» согласно определению 49.

Выход: гамильтонов цикл P

для графа G.

1. Найти минимальное остовное дерево T с матрицей весов [d

];

2. Выделить множество N(T ) всех вершин нечетной степени в T и найти кратчайшее совершенное паросочетание

M в полном графе G с множеством вершин N (T);

3. Построить эйлеров граф G

с множеством вершин {v

, . . . , v

} и множеством ребер T ∪ M;

4. Найти эйлеров обход P

в G

;

5. Построить гамильтонов цикл (соответствующий вложенный тур) P

из P

, последовательным вычеркиванием

посещенных вершин.

2.2 Приближенные алгоритмы с выбираемыми оценками точности

2.2.1 Динамическое программирование для задачи о рюкзаке

В силу важности метода динамического программирования для построения эффективных приближенных алгоритмов

мы остановимся на нем несколько подробнее и проиллюстрируем его на примере следующей NP-полной задачи сумма

размеров:

Задача 22 СУММА РАЗМЕРОВ

Даны натуральные числа a

, . . . , a

, называемые размерами предметов и число B.

Существует ли решение в 0-1 переменных (x

, . . . , x

) уравнения

i=1

= B?

Обозначим через T множество частичных сумм

i=1

для всех 0 − 1 векторов (x

, . . . , x

) и через T(k) - мно-

жество всех частичных сумм

i=1

, которые не превосходят A (T (0) положим равной нулю).

Для того чтобы решить задачу достаточно проверить включение B ∈ T . Если оно выполнено, то ответ ДА, в про-

тивном случае – НЕТ. Множество всех частичных сумм T может быть построено путем просмотра всех 0-1 векторов

(«полным перебором» 2

векторов). Динамическое программирование дает полиномиальный алгоритм, основанный на

рекуррентном соотношении

T (k + 1) = T (k) ∪ (T (k) + a

k+1

где (T (k) + a

k+1

) обозначает множество всех чисел вида s + a

k+1

, s ∈ T (k), которые не превосходят B.

Отметим, что этот алгоритм на самом деле находит все различные значения частичных сумм и, таким образом, дает

точное решение задачи. Число шагов алгоритма есть величина O(nB), поскольку:

1. число циклов равно n;

2. размер каждого множества T (i) не превосходит B.

При небольших значениях A снижение сложности с 2

до Bn дает очевидный эффект, и это характерно для многих

псевдополиномиальных алгоритмов.

Так как задача 22 NP-полна, рассчитывать на построение для нее алгоритма существенно лучшего, чем псевдопо-

линомиальный алгоритм 23 «Сумма размеров» не приходится.

Упражнение 44 Рассмотрим модификацию задачи 23 «Сумма размеров», разрешим даже отрицательные

размеры. Формально: Даны целые числа a

, ∀i ∈ [1 . . . n] − n

≤ a

≤ n

, и число B. Рассмотрим задачу

«Существует ли решение в 0-1 переменных (x

, . . . , x

) уравнения

i=1

= B?»

Существует ли полиномиальный алгоритм для этой задачи?

Рассмотрим теперь внешне похожую NP-полную задачу 21 «Knapsack» и проиллюстрируем как метод динамиче-

ского программирования работает для нее.

Как и прежде, достаточно найти множество T (k) всех пар (c, A), где c — произвольная сумма

i=1

и A —

соответствующая сумма

i=1

≤ B.

Описанный выше способ позволяет рекурсивно построить множество T (n) за Bf

∗

n шагов (напомним, что через

∗

мы обозначаем стоимость оптимального набора). Это аналогично заполнению за n шагов 0/1 таблицы, разме-

ром B × f

∗

, представляющей пространство всевозможных допустимых (не обязательно оптимальных) решений за-

дачи 21 «Knapsack».

Однако уменьшить перебор можно учитывая следующий ключевой факт:

Если на k-ом шаге у нас имеются несколько частичных решений с одинаковой массой, но различной сто-

имостью, то можно для каждой массы оставить решения лишь с максимальной стоимостью, а если есть

несколько частичных решений с одинаковой стоимостью, но различной массой, то можно смело выкинуть

решения с большей массой. При любом из упомянутых действий мы не потеряем оптимальное решение!

Упражнение 45 Докажите это.

Соответственно, это означает отсутствие необходимости держать в памяти все частичные решения, достаточно на

каждой итерации помнить либо о не больше, чем B наиболее «дорогих» частичных решениях, либо о не больше, чем f

∗

наиболее «легких» решениях.

Алгоритм 24 «Рюкзак-ДинПрог» помнит о наиболее «дорогих» частичных допустимых решениях, и тем самым дает

точное решение задачи за время O(nB).

Действительно,

1. число циклов равно n;

Алгоритм 23 Динамическое программирование для задачи 22«Сумма размеров»

def knapsack_sat (A, B):

print , A, , B

T ← {0: [ ]} # Хэш таблица - сумма:разбиение

Цикл по всем предметам a

for i ∈ xrange (len (A)) :

print A[i], ,

← dict (T ) # Копируем T

k−1

в T

old

print T

Цикл по всем полученным частичным суммам

for x ∈ :

if (x + A[i]) ≤ B :

T [x + A[i]] ← [x] + [A[i]]

print , T

if B ∈ T :

print , T [B]

return T [B]

return [ ]