Кузюрин Н.Н. Фомин С.А. Сложность комбинаторных алгоритмов. Курс лекций

Подождите немного. Документ загружается.

(отрицание, дизъюнкция, конъюнкция), образующих полный базис, который будем считать стандартным. В даль-

нейшем имеются в виду схемы именно в этом базисе, если явно не указано что-либо иное.

x NOT x

OR x

AND

0 1 0 0 0 0 0 0

1 0 0 1 1 0 1 0

1 0 1 1 0 0

1 1 1 1 1 1

Конъюнкция и дизъюнкция определяются для произвольного числа булевых переменных аналогичным образом:

конъюнкция равна 1 только тогда, когда все аргументы равны 1, а дизъюнкция равна 0 только тогда, когда все аргу-

менты равны 0. В стандартном базисе они очевидным образом вычисляются схемами (и даже формулами) размера n−1.

Теорема 15 Базис {N OT, OR, AND} — полный.

Доказательство Литералом будем называть переменную или ее отрицание.

Конъюнкцией литералов (это схема и даже формула) легко представить функцию χ

(x), которая принимает значе-

ние 1 ровно один раз: при x = u. Если u

= 1, включаем в конъюнкцию переменную x

, если u

= 0, то включаем в

конъюнкцию ¬x

Произвольная функция f может быть представлена в виде

f(x) =

u:f(u)=1

(x). (1.13)

В таком случае говорят, что f представлена в дизъюнктивной нормальной форме (ДНФ), т.е. как дизъюнкция

конъюнкций литералов.

Как уже говорилось, дизъюнкция нескольких переменных выражается формулой в стандартном базисе. 2

Определение 39 Размером схемы называется количество присваиваний в схеме.

Определение 40 Глубиной схемы называется максимальное число элементов на пути от входов к выходу.

Определение 41 Минимальный размер схемы в базисе F, вычисляющей функцию f , называется схемной слож-

ностью функции f в базисе F и обозначается c

F(f )

Переход от одного полного конечного базиса к другому полному конечному базису меняет схемную сложность

функций на множитель O(1). Так что в асимптотических оценках выбор конкретного полного базиса неважен и по-

этому будем использовать обозначение c(f) для схемной сложности f в конечном полном базисе.

Каждый предикат f на множестве {0, 1}

∗

задает последовательность булевых функций f

: {0, 1}

→ {0, 1} следу-

ющим образом:

, x

, . . . , x

) = f(x

. . . x

где справа стоит характеристическая функция предиката f.

Определение 42 Предикат f принадлежит классу P/poly, если

c(f

) = poly(n).

Теорема 16 P ⊂ P/poly.

Доказательство Если МТ работает за полиномиальное время, то и память, которую она использует, ограничена по-

линомом. Поэтому весь процесс вычисления на входном слове x длины n можно представить таблицей вычисления

размера T × S, где T = poly(n), S = poly(n).

t = 0 Γ

0,1

t = 1

. . .

t = j Γ

left

right

t = j + 1 Γ

. . .

t = T . . .

| {z }

S клеток

Далее нам еще потребуется и конъюнктивная нормальная форма (КНФ) — конъюнкция дизъюнкций литералов.

Строка с номером j таблицы задает состояние МТ после j тактов работы. Символы Γ

j,k

, записанные в таблице,

принадлежат алфавиту S × {∅ ∪ Q}. Символ Γ

j,k

определяет пару (символ, записанный в k-й ячейке после j так-

тов работы; состояние управляющего устройства после j тактов работы, если головка находится над k-й ячейкой, в

противном случае второй элемент пары — ∅). Для простоты также считаем, что если вычисление заканчивается при

некотором входе за T

< T тактов, то строки c номерами, большими T

, повторяют строку с номером T

Построить схему, вычисляющую значения предиката на словах длины n, можно следующим образом. Состояние

каждой клетки таблицы можно закодировать конечным (не зависящим от n) числом булевых переменных. Имеются

локальные правила согласования, т. е. состояние каждой клетки Γ в строке ниже нулевой однозначно определяется

состояниями клеток в предыдущей строке, лежащих непосредственно над данной (Γ

), левее данной (Γ

left

) и правее

данной (Γ

right

). Каждая переменная, кодирующая состояние клетки Γ, есть функция от переменных, кодирующих со-

стояния клеток Γ

left

, Γ

right

. Все эти функции могут быть вычислены схемами конечного размера. Объединяя эти

схемы, получим схему, вычисляющую все переменные, кодирующие состояния клеток таблицы; размер этой схемы бу-

дет O(ST ) = O(n

O(1)

Осталось заметить, что переменные, кодирующие часть клеток нулевой строки, определяются входным словом, а

переменные, кодирующие остальные клетки нулевой строки, являются константами. Чтобы узнать результат вычисле-

ния, нужно определить символ, записанный в нулевой ячейке ленты в конце вычисления.

Без ограничения общности можно считать, что состояния клеток таблицы кодируются так, что одна из кодирующих

переменных равна 1 только в том случае, когда в ячейке записана 1. Тогда значение этой переменной для кода Γ

T,0

будет результатом вычисления. 2

Справедливо следующее усиление теоремы.

Теорема 17 f принадлежит P тогда и только тогда, когда

1. f ∈ P/poly;

2. существует МТ, которая по числу n за время poly(n) строит схему вычисления f

Доказательство =⇒ Данное в доказательстве теоремы 16 описание нетрудно превратить в МТ, которая строит схе-

му вычисления f

за полиномиальное по n время (схема f

имеет простую структуру: каждая переменная связана с

предыдущими одними и теми же правилами согласования).

⇐= Столь же просто. Вычисляем размер входного слова. Затем строим по этому размеру схему S

|x|

вычисления

|x|

, используя указанную в условии 2) машину. После этого вычисляем S

|x|

(x) на машине, которая по описанию схемы

и значениям входных переменных вычисляет значение схемы за полиномиальное от длины входа время. 2

Упражнение 24 Постройте полиномиальный алгоритм, определяющий, является ли данный базис полным.

Базисные функции заданы таблицами значений.

Упражнение 25 Пусть c

есть максимум сложности c(f)

по всем булевым функциям f от n переменных. Докажите, что 1,99

< c

< 2,01

при достаточно больших

Упражнение 26 Покажите, что любую функцию можно вычислить схемой глубины не более 3 из элементов

NOT и из элементов AN D и OR с произвольным числом входов.

Упражнение 27 Докажите, что если из схемы глубины O(log n), вычисляющей f : {0, 1}

→ {0, 1}

, выбросить

все несущественные присваивания, то полученная схема имеет полиномиальный по n + m размер.

Упражнение 28 Постройте схему, которая сравнивает два n-битовых числа и имеет размер O(n), а глубину

O(log n).

Упражнение 29 1. Постройте схему сложения двух n-битовых чисел размера O(n).

2. Тот же вопрос, если дополнительно потребовать, чтобы глубина схемы была O(log n).

Упражнение 30 Функция MAJ {0, 1}

→ {0, 1} равна 1 на двоичных словах, в которых число единиц больше

числа нулей, и 0 — на остальных словах. Постройте схему, вычисляющую эту функцию, размер схемы должен

быть линеен по n, глубина — O(log n log log n).

Упражнение 31 Постройте схему размера poly(n) и глубины O(log

n), которая проверяет, связаны ли путём

две вершины в графе. Граф на m вершинах, которые помечены числами от 1 до m, задаётся n = m(m − 1)/2

булевыми переменными. Переменная x

, где i < j, определяет, есть ли в графе ребро, соединяющее вершины

i и j.

Упражнение 32 Пусть схема глубины 3 из элементов N OT и из элементов AND и OR с произвольным чис-

лом входов вычисляет сл ожение n битов по модулю 2 (функция P ARIT Y ). Покажите, что размер схемы не

меньше c

для некоторого c > 1.

Упражнение 33 Пусть f

, f

, . . . f

, . . . — последовательность булевых функций от

1, 2, . . . n, . . . аргументов. Покажите, что следующие два свойства равносильны:

1. существует последовательность вычисляющих эти функции формул, размер которых не превосходит

полинома от n;

2. существует последовательность вычисляющих эти функции схем глубины O(log n) из элементов NOT ,

AND и OR (с двумя входами).

Упражнение 34 Докажите, что существует разрешимый предикат, который принадлежит P/poly, но не

принадлежит P .

1.7 Коммуникационная сложность.

С появлением и развитием телекоммуникационных сетей и распределенных вычислений, стали возникать новые типы

ресурсных ограничений: коммуникационные.

О них не могло быть и речи, пока компьютеры были вне сети — хватало рассмотренных в разделе 1.3.4 временных и

пространственных ресурсных ограничений и соответствующих мер сложности задач. Обьединение компьютеров в ло-

кальные сети также редко приводило к тому, что «бутылочным горлышком» при решении какой-либо задачи является

именно пропускная способность сети, или высокая стоимость трафика.

Однако, с появлением глобальных сетей стали создаваться ситуации, когда, например, несколько мощных научных

центров, обладающих огромными вычислительными ресурсами, пытаются обьединить усилия для решения некоторой

вычислительной задачи, либо когда филиалам транснациональной корпорации требуется выполнить возможно алго-

ритмически несложные действия, но над распределенными базами данных, при этом основной стоимостью становиться

стоимость коммуникаций. Как напрямую, путем оплаты услуг провайдера, так опосредовано — когда передача боль-

ших обьемов данных занимает много дорогостоящего времени и тормозит вычисления.

Таким образом, появилось новое ресурсное ограничение — стоимость коммуникации, и соответственно появи-

лась новая мера сложности алгоритмических задач — коммуникационная сложность.

При исследовании коммуникационной сложности задачи полагают, что входные данные некоторым образом рас-

пределены между n > 1 участниками, каждый из которых обладает неограниченными вычислительными ресурсами, и

необходимо установить нижние и верхние оценки для трафика (обьема сообщений), необходимого для решения задачи.

Существуют различные модели коммуникации, обуславливающие различные меры коммуникационной сложности: мо-

дели с произвольным числом участником, модели с произвольным распределением данных и т.п. Наиболее стандартной

и классической является модель с двумя участниками и симметричным распределением между ними входных данных

Их задача — совместно вычислить некоторую булеву функцию. Участники по очереди обмениваются сообщениями

фиксированной длины (как вариант — однобитовыми сообщениями), пока одним из участников не будет получен ответ.

Коммуникационная сложность оценивается в терминах O(f(n)), где n — длина входа, (например, число аргумен-

тов вычисляемой булевой функции). Сразу заметим, что для любой задачи такого рода существует тривиальное реше-

ние, заключающееся в пересылке одним участком другому всех своих данных — O(n). Это является верхней оценкой

коммуникационной сложности для задач с двумя участниками, поэтому интерес составляет получение более низких

оценок — полилогарифмических или константных.

Приведем примеры нескольких задач, с установленными для них оценками коммуникационной сложности.

Задача 14 «ЧЕТНОСТЬ» Алиса и Боб имеют по битовой строке длины n. Необходимо вычислить четность

числа бит строки-конкатенации.

Легко видеть, что коммуникационная сложность задачи 14 равна O(1). Действительно, Алисе достаточно вычис-

лить четность своей строки (один бит), и передать ее Бобу.

Задача 15 «СРАВНЕНИЕ» Алиса и Боб имеют битовые строки длины n: X = (x

, . . . , x

) и Y = (y

, . . . , y

)

соответственно. Нужно сравнить эти строки (проверить на эквивалентность).

Оказывается (доказано), что нижние оценки для задачи 15 совпадают с тривиальными верхними оценками, и таким

образом, коммуникационная сложность точного решения задачи 15 есть Ω(n).

Задача 16 «СУММА БИТ» Алиса и Боб имеют по битовой строке длины n. Одинаково ли число единиц в би-

товых строках?

Простой алгоритм для задачи 16: «Алиса высылает Бобу сумму единиц в своей строке», имеет коммуникационную

сложность O(log n).

С другой стороны, доказано (здесь мы не будем касаться методик получения нижних оценок), что этот алгоритм

также является оптимальным.

Вот задача (правда вычисляется не булевая функция, а число), требующая менее тривиального оптимального алго-

ритма:

Задача 17 «МЕДИАНА»

Алиса и Боб имеют по подмножеству множества (1, 2, . . . , n). Необходимо найти элемент-медиану

обьединении этих подмножеств.

Упражнение 35 Постройте алгоритм для задачи 17 с коммуникационной сложностью O(log

n).

Как и в многих задачах связанных с коммуникациями (например, в криптографических постановках) этих двух участников зовут Алиса и Боб.

элемент, занимающий dm/2e место в упорядоченном массиве из m элементов

Упражнение 36 Постройте алгоритм для задачи 17 с коммуникационной сложностью O(log n).

Кроме коммуникационной сложности точного решения задачи и детерминированных алгоритмов рассматривают

(аналогично с разделом 3) коммуникационную сложность вероятностных алгоритмов. Т.е. участники могут применять

вероятностные алгоритмы, каждый из которых использует либо общий для всех источник случайных чисел (public

coins, менее распространенная модель), либо собственный датчик-источник случайных чисел (private coins, более

распространенная модель, далее будем рассматривать только ее).

Допустима некоторая вероятность P

err

ошибки, а количество переданных бит измеряется также, как и в детерми-

нированном случае.

Также, как и в случае с временной сложностью, применения вероятностных алгоритмов может дать существенный

выигрыш и в коммуникационной сложности.

Итак, рассмотрим задачу 15 (СРАВНЕНИЕ), и попробуем получить алгоритм, более коммуникационно-эффективный,

чем тривиальный.

Выберем случайное простое p из интервала [1 . . . m], m — целое. Обозначим

p(X) = X mod p,

p(Y ) = Y mod p.

Очевидно, что если строки X и Y совпадают, то p(X) = p(Y ).

Ошибка, т.е. X и Y не совпадают, при p(X) = p(Y ), произойдет, если |X − Y | делится на p без остатка. Оценим

вероятность ошибки.

Обозначим через π(N) число простых чисел, не превосходящих N. Известна следующая оценка: π(N) ∼

ln N

. Так

как длина битовых строк равна n, то |X − Y | ≤ 2

, и справедлива

Лемма 19 Число различных простых делителей любого числа меньшего 2

не превосходит n.

Пусть A(n) — число простых, делящих X − Y . Тогда вероятность ошибки равна отношению числа простых, делящих

X − Y , к числу всех простых из интервала [1 . . . m], то есть

err

A(n)

π(m)

≤

π(m)

n ln m

причем m > n.

Для того, чтобы вероятность ошибки была мала, m должно быть достаточно велико. Пусть m = n

, c = const, тогда

err

nc ln n

c ln n

c−1

Видно, что при больших n, P

err

очень мала. Например, если c = 2, для n = 10

, будет m = 10

, а

err

≤

n ln m

2 ln n

≈ 2.3 · 10

−4

При этом, для сравнения двух строк достаточно переслать выбранный простой делитель (≤ m) и остаток от деления

(< m), т.е. потратить не более 2 log m = O(log n) бит.

1.8 Диаграмма классов сложности

В этом разделе мы постараемся кратко резюмировать информацию по классам сложности задач, встречавшихся в

разделе 1.

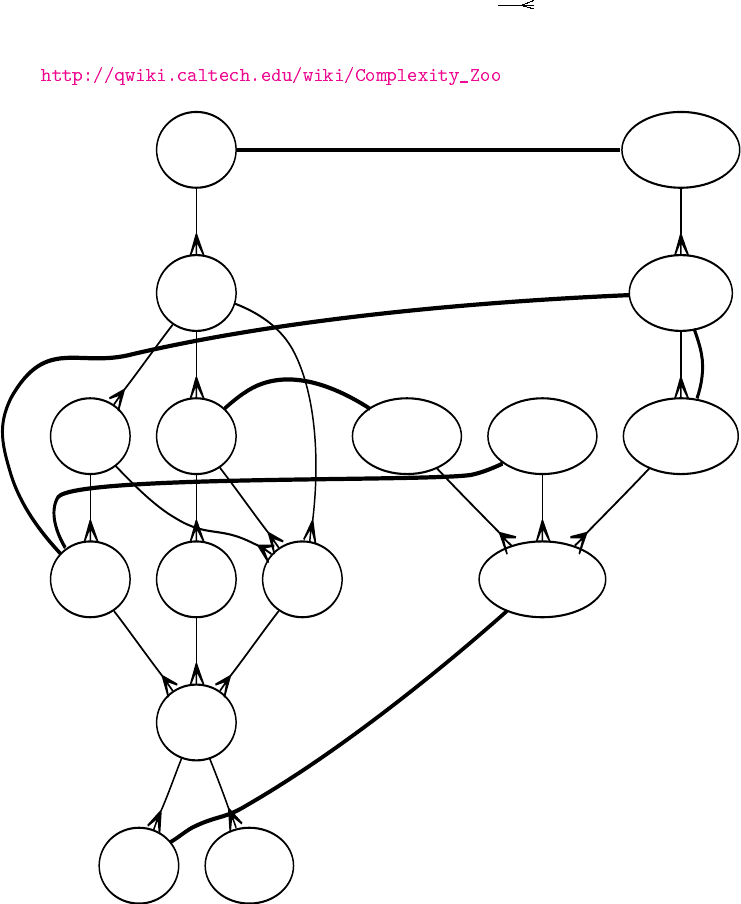
Мы свели их в единую диаграмму на Рис.1.10. Мы изобразили через отношения вложенности, а жирными

линиями — эквивалентность. Разумеется, мы не ставили целью отобразить все классы сложности — это вряд ли воз-

можно на одной диаграмме, т.к. сейчас насчитывается не менее четырехсот различных классов сложности («Зоопарк

Классов Сложности» , упоминает о 442 классах).

ZPP

PCP(log,q=2)

equal

PCP(log,1)

equal PCP(0,poly)

equal

coNP

BPP

inRP

coRP

PSPACE

NEXP

in in in in

PCP(poly,0)

equal

PCP(log,log)

in equal

PCP(poly,poly)

in in

equal

Рис. 1.10: Иерархия некоторых классов сложности.

Глава 2

Приближенные алгоритмы с

гарантированными оценками точности

2.1 Приближенные алгоритмы с фиксированными оценками точности

2.1.1 Жадный алгоритм в задаче о покрытии

Одним из общих подходов к решению NP-трудных задач бурно развивающимся в настоящее время является разра-

ботка приближенных алгоритмов с гарантированными оценками качества получаемого решения.

Определение 43 Приближенный алгоритм имеет мультипликативную точность D, если он при любых

исходных данных находит допустимое решение со значением целевой функции, отличающемся от оптиму-

ма не более, чем в D раз.

Одной из простейших эвристик часто применяемых при решении различных задач является так называемая жадная

эвристика. Для некоторых задач, например для задачи об остовном дереве минимального веса в графе, фактически эта

эвристика позволяет найти оптимальное решение (см. Алгоритм Прима).

В более трудных случаях она позволяет получать гарантированные оценки точности получаемого с их помощью

решения.

Рассмотрим сейчас жадную эвристику для классической NP-трудной задачи — задачи о покрытии.

Задача 18 «Покрытие множества»

Пусть на m-элементном множестве X задано некоторое семейство его подмножеств F = {S

, . . . , S

}и

X = ∪

i=1

Надо найти минимальное по числу подмножеств подсемейства P ⊆ F , обладающее свойством покрытия,

то есть нахождении минимального J ⊆ {1, 2, . . . , n} такого, что

X = ∪

i∈J

(2.1)

Число |J| называется размером минимального покрытия.

Известно, что задача о покрытии NP-полна. По этой причине трудно надеяться на существование полиномиаль-

ного алгоритма ее решения.

Применительно к задаче о покрытии жадная эвристика заключается в выборе на каждом шаге подмножества, по-

крывающего максимальное число еще непокрытых элементов. Работа этого алгоритма проиллюстрирована на Рис. 2.1.1,

где по вертикали представлены подмножества элементов, по горизонтали элементы (т.е. каждый графический обьект

с координатами x, y представляет принадлежность некоторого элемента x подмножеству y), темным цветом выделены

выбранные алгоритмом подмножества. Эффективность описанного приближенного алгоритма для задачи о покрытии

очевидна.

Оценим сейчас точность, которую жадный алгоритм гарантирует в задаче о покрытии.

Пусть X

— число непокрытых после k-го шага, M — размер минимального покрытия.

Имеем:

k+1

≤ X

−

= X

(1 − 1/M). (2.2)

Set covering, в англоязычной литературе

Рис. 2.1: Иллюстрация работы жадного алгоритма для задачи о покрытии

Упражнение 37 Докажите неравенство (2.2).

≤ m(1 − 1/M)

≤ m exp(−

)

Найдем наибольшее k

при котором

m exp(−

) ≥ 1.

Тогда при k

= k

+ 1

< 1,

что означает, что все элементы покрыты.

При этом

/M ≤ 1 + ln m,

значит размер покрытия, построенного жадным алгоритмом, превосходит минимальное не более, чем в 1 + ln m раз.

Упражнение 38 Постройте пример, где оценка O(1 + ln m) размера покрытия построенного жадным алго-

ритмом достигается по порядку. Указание: достаточно рассмотреть случай, когда размер минимального

покрытия M = 2.

Упражнение 39 Постройте пример, где эта оценка достигается асимптотически.

Рассмотрим вариант задачи 18 «Set Covering».

Задача 19 «K-покрытие» На m-элементном множестве X задано некоторое семейство его подмножеств

F = {S

, . . . , S

}. Надо выбрать k подмножеств из F , чтобы мощность их объединения была максимальна.

Оказалось жадный алгоритм дает хорошие результаты и для этой задачи.

Теорема 18 Жадный алгоритм гарантирует мультипликативную точность 1−e

−1

в задаче 19 «К-покрытие».

Доказательство Пусть X

обозначает число покрытых элементов после i-го шага жадного алгоритма, а M — опти-

мум в задаче о k-покрытии. Справедливо следующее неравенство (см. упражнение 37):

i+1

≥ X

M − X

+ X



1 −



Решая это реккурентное неравенство, получим:

≥

1 +



1 −





1 −



+ . . . +



1 −



1 −



1 −



k+1

= M

1 −



1 −



k+1

≥ M



1 − exp



−

k + 1



≥ M(1 − e

−1

2.1.2 Приближенные алгоритмы для задачи покрытия с минимальной суммой

Определение 44 Гиперграф — неформально это обобщение понятия графа, в котором, вместо ребер, каж-

дое из которых соединяет только две вершины, используются гиперребра, соединяющии любое непустое

число вершин. Частные случаи гиперграфов — r-однородные гиперграфы, в которых все гиперребра соеди-

няют ровно r-вершин.

Заметим, что «обычные» графы являются 2-однородными гиперграфами.

Определение 45 Будем говорить, что в гиперграфе H(V, E) вершина покрывает все инцидентные ей ребра,

а количество инцидентных ей ребер является ее степенью.

Задача 20 «Min Sum Set Cover»,«MSSC» — «покрытие гиперграфа с минимальной суммой». Для заданного

гиперграфа H(V, E), нужно найти линейное упорядочение вершин f (биекция):

f : V → {1, 2, . . . , |V |},

которое минимизирует

f(e), где f (e) определяется как минимум f(v) по всем v ∈ e.

Видно, что задача 20 «MSSC» похожа на задачу 18 «Set Covering», интересно исследовать качество простого

жадного алгоритма, раздающего последовательно номера от 1 до |V |, чтобы «меньшие» номера доставались как можно

большему числу ребер (См. алгоритм 18 «Greedy MSSC»).

Упражнение 40 Приведите пример гиперграфа, для которого алгоритм 18 «Greedy MSSC» находит неопти-

мальное решение.

Теорема 19 Алгоритм 18 «Greedy MSSC» гарантирует мультипликативную точность, не превышающую 4.

Доказательство Введем следующие обозначения, для решаемой алгоритмом 18 «Greedy MSSC» задачи 20 «MSSC»,

заданной гиперграфом H(V, E):

• opt — оптимальное значения.

• greedy — значение, выдаваемое алгоритмом 18 «Greedy MSSC».

• e — индекс гиперребра.

• f

∗

(v), f

∗

(e) — значения функции f, соответствующие оптимальному решению.

f(e) = opt.

• k = 1, 2, . . . , n — индекс, номер шага алгоритма и номер выбранной на этом шаге вершины.

• X

обозначает множество ребер, покрываемых (впервые) на шаге k, и x

= |X

• R

обозначает множество ребер, непокрытых до шага k, и r

= |R

|. Отметим, что

= E − ∪

k−1

j=1

= ∪

j=k

, r

j=k

Рассмотрим, значение выдаваемое алгоритмом:

greedy =

k=1

k|X

| =

k=1

k · x

k=1

. (2.3)

Определим для каждого шага алгоритма (и выбранной на этом шаге вершины) стоимость p

. Стоимость p

для гиперребра e определим как стоимость p

первой вершины k, выбранной алгоритмом и покрывающим ребро e.

Теперь можно выразить greedy через p

, если разбить суммирование по множествам ребер, включаемых на каждом

шаге алгоритма:

greedy =

· p

. (2.4)

Рассмотрим гистограмму e → f

∗

(e), в которой имеется |E| столбцов, по одному для каждого гиперребра, высота

стобца e равна f

∗

(e), а столбцы упорядочены по возрастанию высоты. Таким образом, получаем гистограмму с неубы-

вающими целочисленными высотами, с площадью

f(e) = opt.

Рассмотрим теперь другую гистограмму e → p

, в котором ребра упорядочены в соответствии с порядком, в ко-

тором они были покрыты жадным алгоритмом, а высота каждого ребра равна его стоимости. Общая площадь гисто-

граммы будет равна

= greedy. Заметим, что эта гистограмма не обязательно будет целочисленной (очевидно), и

необязательно монотонной (см. упражнение 41). Мы получаем монотонно невозрастающую диаграмму, общая площадь

которой равна

= greedy.

Гистограммы для примера, рассмотренного в алгоритме 18 «Greedy MSSC», приведены ниже (первая гистограм-

ма желтая с черными границами, вторая незакрашеная с синими границами).