Кузюрин Н.Н. Фомин С.А. Сложность комбинаторных алгоритмов. Курс лекций
Подождите немного. Документ загружается.

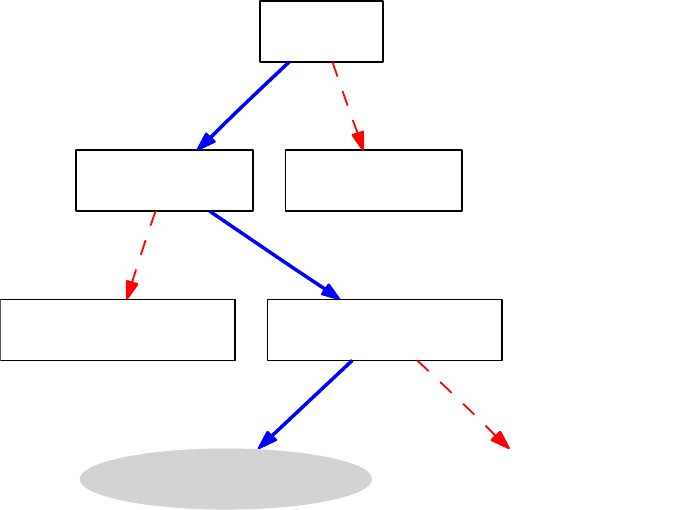
EX=4.78
EX(x1=0)=2.5
x1=0
EX(x1=1)=6.4
x1=1
EX(x1=0,x2=0)=5.3
x2=0
EX(x1=0,x2=1)=2.1
x2=1
EX(x1=0,x2=1,x3=0)=1
x3=0
EX(x1=0,x2=1,x3=1)=4
x3=1
Рис. 3.1: Дерандомизация на основе минимизации оценок матожидания.
EX = P{x
1
= 1}EX(x| x
1
= 1) + P{x
1
= 0}EX(x| x
1
= 0)
= p
1
EX(x| x
1
= 1) + (1 − p
1
)EX(x| x
1
= 0)
≥ p
1
EX(x| x
1
= d
1
) + (1 − p
1
)EX(x| x
1
= d
1
)
= (p
1
+ 1 − p
1
)EX(x| x
1
= d
1
) = EX(x| x
1
= d
1
).
Продолжая эту цепочку неравенств для каждого шага, получаем на последнем n-м шаге
EX ≥ EX(x| x
1
= d
1
, . . . , x
n
= d
n
).
Но
EX(x| x
1
= d
1
, . . . , x
n
= d
n
) = X(d
1
, . . . , d
n
),
и для построенного вектора ˆx = (d
1
, . . . , d
n
) выполнено неравенство (3.8).
Как оценить число шагов описанной процедуры? На каждой итерации вычисляются два условных мат. ожидания
(f
0
и f
1
) и затем находится минимум этих величин. Если это делается за время O(L), то при общем числе итераций n,
получим оценку O(nL). Таким образом, изложенный общий метод позволяет осуществлять «дерандомизацию» если у
нас есть эффективный алгоритм вычисления условных мат. ожиданий (или условных вероятностей).
Теперь используем описанный выше метод условных вероятностей для задачи 25 «MAXSAT» (MAX-SAT). Мат.
ожидание X равно сумме вероятностей невыполнения скобок:
EX =
m
X
j=1
P
j
, (3.9)
где вероятность невыполнения j-й дизъюнкции есть
P
j
= P
X
i∈C
+
j
x
i
+
X
i∈C
−
j
(1 − x
i
) = 0
.
Для полученного вектора (d
1
, . . . , d
n
) выполнено неравенство
X(x
1
= d
1
, . . . , x
n
= d
n
) ≤ EX. (3.10)
111
Из теоремы 27 следует, что EX ≤ (1/e)m и из (3.10) вытекает, что X(x
1
= d
1
, . . . , x
n
= d
n
) ≤ (1/e)m.
Таким образом, мы находим допустимый 0-1 вектор x = (x
1
, . . . , x
n
) с гарантированной верхней оценкой для целе-
вой функции.
Важный вопрос заключается в том как эффективно вычислять условные мат. ожидания. Предположим, значения
первых k переменных уже определены и I
0
— множество индексов переменных, значения которых равны 0,а I
1
—
множество индексов переменных, значения которых равны 1.
Нетрудно проверить, что если I
0
∩ C
−
j
6= ∅ или I
1
∩ C
+
j
6= ∅, то P
j
= 0. В противном случае,
P
j
=
Y
i∈C
+
j
\I
0
(1 − p
i
) ·
Y
i∈C
−
j
\I
1
p
i
. (3.11)
Запишем этот алгоритм более формально (алгоритм 31 «MAX-SAT дерандомизация»).
Алгоритм 31 Дерандомизация вероятностного алгоритма 29 «вероятностный MAX-SAT» по методу условных веро-
ятностей
Вход: Формулировка задачи 25 «MAXSAT» в виде (3.6)
Выход: (y
1
, . . . , y
m
) — приближенное решение (3.6).
(p
1
, . . . , p
n
) ← решения линейной релаксации ( 3.7)
for all i ∈ {1..m} do
f
0
= EX(x| x
i
= 0) {Вычисляется через (3.11)}
f
1
= EX(x| x
i
= 1) { и (3.9)}
if f
0
< f
1
then
x
i
← 0
else
x
i
← 1
end if
end for
return x
Упражнение 57 Покажите, что можно организовать вычисление f
0
и f
1
таким образом, что сложность
алгоритма 31 «MAX-SAT дерандомизация» будет O(mn).
3.4.4 Дерандомизация вероятностного алгоритма Луби нахождения максимального по вклю-
чению независимого множества в графе
Пусть G = (V, E) — неориентированный граф с n вершинами и m ребрами. Подмножество вершин I ⊆ V называется
независимым в G если никакое ребро из E не содержит обе своих конечных вершины в I.
Определение: Независимое множество I называется максимальным по включению, если оно не содержится в
качестве собственного подмножества в другом независимом множестве в G.
Напомним, что ранее мы рассматривали вероятностный алгоритм Parallel MIS:
Вход: Граф G = (V, E).
Выход: Максимальное по включению множество I ⊆ V .
1. I := ∅.
2. repeat
2.1. for all v ∈ V do (in parallel)
if d(v) = 0 then add v to I and delete v from V
else mark v with probability 1/2d(v).
2.2. for all (u, v) ∈ E do (in parallel)
if both u and v are marked
then unmark the lower degree vertex.
2.3. for all v ∈ V do (in parallel)
if v is marked then add v to S.
2.4. I := I ∪ S.
2.5. delete S ∪ G(S) from V , add all incident edges from E.
until V = ∅.
Идея дерандомизации этого алгоритма заключается в том, чтобы покать, что вероятностный анализ работает ана-
логичным образом, даже если пометки вершин делаются не полностью независимо, а попарно независимо. Отметим,
единственное место в анализе алгоритма, где использовалась независимость пометок была лемма 1.
112
Справедлива следующая
Лемма. Если в алгоритме Parallel MIS случайные пометки вершин делаются попарно независимо, то вероятность,
что хорошая вершина принадлежит множеству S ∪ Γ(S) не меньше, чем 1/24.
Ключевое преимущество попарной независимости состоит в том, что только O(log n) случайных бит достаточно для
порождения всех точек соответствующего вероятностного пространства.
Число точек в таком пространстве есть O(n
c
) и может быть просмотрено полным перебором за полиномиальное
время.
Доказательство леммы. Единственное место, где использовалась полная независимость пометок вершин была
нижняя оценка вероятности, что хорошая вершина становится помеченной. Была использована следующая оценка:
Пусть X
i
, 1 ≤ i ≤ n — {0, 1} случайные величины и p
i
= Pr(X
i
= 1). Если X
i
независимы в совокупности, то
Pr(
n
X
1
X
i
> 0) ≥ 1 −
n
Y
1
(1 − p
i
).
Мы заменим эту оценку соответствующей оценкой для попарно независимых случайных ведичин.
Утверждение. Пусть X
i
, 1 ≤ i ≤ n — {0, 1}случайные величины и p
i
= Pr(X
i
= 1). Если X
i
попарно независимы,
то
Pr(
n
X
1
X
i
> 0) ≥
1
2
min{
1
2
,
n
X
1
p
i
}.
Доказательство. Предположим, что
P
p
i
≤ 1/2.
Обозначим через Y
i
событие X
i
= 1. Имеем по формуле включений-исключений:
Pr(∪
n
1
Y
i
) ≥
X
i
Pr(Y
i
) −
1
2
X
i,j
Pr(Y
i
∧ Y
j
) ≥
X
i
p
i
−
1
2
X
i,j
p
i
p
j
=
X
i
p
i
−
1
2
(
X
i
p
i
)
2
≥
X
i
p
i
1 −
1
2
X
i
p
i
!
≥
1
2
X
i
p
i
.
Если
P
i
p
i
> 1/2, то ограничим индексы суммирования по подмножеству S ⊆ [n] такому, что 1/2 ≤
P
i
p
i
≤ 1, и
повторим то же доказательство.
Завершим теперь доказательство леммы.
Напомним, что вершина v ∈ V называется хорошей, если она имеет не менее d(v)/3 соседних вершин степени не
более d(v). В противном случае вершина называется плохой.
Покажем, что если v — хорошая вершина, то вероятность, что найдется помеченная вершина из Γ(v) не меньше
1/12. Обозначим эту верояность через Pr(Γ(v)
marked
).
Обозначим Γ
∗
(v) = {w ∈ Γ(v)| d(w) ≤ d(v)}. По определению хорошей вершины |Γ
∗
(v)| ≥
1
3
d(v). Используя
доказанную выше оценку для попарно независимых случайных величин имеем:
Pr(Γ(v)
marked
) ≥
1
2
min{
1
2
,
X
w∈Γ(v)
1
2d(w)
} ≥
1
2
min{
1
2
,
X
w∈Γ
∗
(v )
1
2d(w)
} ≥
1
2
min{
1
2
,
X
w∈Γ
∗
(v )
1
2d(v)
} ≥
1
2
min{
1
2
,
1
3
d(v)
1
2d(v)
} ≥
1
2
min{
1
2
,
1
6
} =
1
12
.
Используя лемму 2 из анализа вероятностного алгоритма Луби
"Лемма 2. В течение каждой итерации, если вершина помечена, то она выбирается в S с вероятностью не менее
1/2."
и используя тот факт, что в ее доказательстве использовалась только попарная независимость, получаем доказа-
тельство нашей леммы.
113
Попарная независимость для неодинаково распределенных случайных величин. Конструкция.
Покажем теперь, осуществить дерандомизацию путем полного перебора точек из вероятностного пространства.
Для этого нужна конструкция небольшого вероятностного пространства со свойством попарной независимости соот-
ветствующих случайных величин. Опишем эту конструкцию.
Выберем простое число p, n ≤ p ≤ 2n. Известно, что такое число всегда существует. Для каждой вершины u
выберем целое a
u
такое, что a
u
/p ≈ 1/2d(u) и интервал A
u
, |A
u
| = a
u
в Z
p
.
Пусть X(u) — случайная величина, полученная путем равномерного выбора x, y ∈ Z
p
следующим образом: X(u) =
1, если xu + y ∈ A
u
, и нулю в противном случае.
Это значит, что Pr(X(u) = 1) = a
u
/p ≈ 1/2d(u) поскольку
Pr
x,y
(X(u) = 1) = Pr(∃a ∈ A
u
: xu + y = a) =
X
a∈A
u
Pr(x = (a − y)u
−1
) =
X
a∈A
u
1
p
=
a
u
p
.
Для доказательства попарной независимости, достаточно показать, что
Pr(X(u) = 1, X(v) = 1) = Pr(X(u) = 1)Pr(X(v) = 1) =
a
u
a
v
p
2
.
Имеем:
Pr(X(u) = 1, X(v) = 1) = Pr(∃a ∈ A
u
, b ∈ A
v
: xu + y = a, xv + y = b) =
Pr(∃a ∈ A
u
, b ∈ A
v
: xu + y = a, xv + y = b) =
X
a∈A
u
, b∈A
v
Pr(xu + y = a, xv + y = b) =
X
a∈A
u
, b∈A
v
1
p
2
=
a
u
a
v
p
2
.
114

Глава 4
Криптография
4.1 Генераторы
4.1.1 Псевдослучайные генераторы. Генератор Нисана-Вигдерсона
Под псевдослучайным генератором обычно понимают отображение, переводящее более короткую (случайную) строку
в более длинную (псевдослучайную). Более формальные требования определяют различные типы псевдослучайных
генераторов.
Рассмотрим одно из определений псевдослучайного генератора.
Определение 66 Детерминированный алгоритм G : {0, 1}
t
→ {0, 1}
m
, m > t, называется (S, ε)-псевдослучайным
генератором, если для любой булевой схемы C размера не превосходящего S,
|Pr
r
{C(r) = 1} − Pr
x
{C(G(x)) = 1}| ≤ ε.
Для булевой функции f : {0, 1}
n
→ {0, 1} ее трудностью H(f) называется наибольшее значение S такое, что для
любой булевой схемы размера не более S,
Pr
x
{C(x) = f(x)} ≤
1
2
+
1
S
.
Мы рассмотрим сейчас классическую конструкцию Нисана-Вигдерсона (1988, STOC)
Пусть f — булева функция f : {0, 1}
l
→ {0, 1}. Пусть трудность функции f есть величина H(f) = O(m
2
),
m = 2
rl
, r > 0. Определим семейство подмножеств:
S
1
, . . . , S
m
⊆ {1, . . . , t}, t = O(l/r)
|S
i
| = l
|S
i
∩ S
j
| ≤ rl = log m
Тогда псевдослучайный генератор
NW
f(S
1
,...,S
m
)
: {0, 1}
t
→ {0, 1}
m
определяется следующим образом:
NW
f(S
1
,...,S
m
)
(z) = f(z|S
1
), . . . , f(z|S
m
),
где z|S = z
s
1
, z
s
2
, . . . , z
s
l
, если S = {s
1
, . . . , s
l
} ⊆ {1, . . . , t}.
z|k обозначает k-й бит в последовательности z.
Лемма. Если S
1
, . . . , S
m
⊆ {1, . . . , t}, t = O(l/r) таковы, что |S
i
| = l и |S
i
∩ S
j
| ≤ log m, то для каждой булевой
функции f с H(f) = O(m
2
) и любой схемы C такой, что
|Pr
z
[C(NW
f(S
1
,...,S
m
)
(z) = 1] − Pr
r
[C(r) = 1]| > δ,
существует схема A размера ≤ O(m
2
) + size(C) такая, что
Pr
x
[A(x) = f(x)]| ≥ 1/2 + δ/m.
115
Доказательство. Представим алгоритм A.
Вход: x ∈ {0, 1}
l
Выход: ∈ {0, 1}
Рассмотрим последовательночть строк.
H
0
= r
1
, r
2
, . . . , r
m
— полностью случайная последовательность
H
1
= f(z|S
1
), r
2
, . . . , r
m
H
i−1
= f(z|S
1
), . . . , f(z|S
i−1
), r
i
, . . . , r
m
H
i
= f(z|S
1
), . . . , f(z|S
i
), r
i+1
, . . . , r
m
H
m
= NW (z)
Если |Pr[C(H
m
) = 1] − Pr[C(H
0
) = 1]| > δ, тогда для некоторого i должно быть выполнено
|Pr[C(H
i
) = 1] − Pr[C(H
i−1
) = 1]| > δ/m.
Значит,
Pr
x,y , r
i
,...,r
m
[A(x) = f(x)] = E
y ,r
i
,...,r
m
(Pr
x
[A(x) = f(x)]) ≥ 1/2 + δ.
Отсюда вытекает, что
∃y, r
i
, . . . , r
m
: Pr
x
[A
y ,r
i
,...,r
m
(x) = f(x)]) ≥ 1/2 + δ. (1)
Финальный алгоритм будет A
y , r
i
,...,r
m
с параметрами, удовлетворяющими (1).
При фиксированном y только |y| = O(log m) бит необходимы для вычисления f
i
(x, y). Значит, f
i
(x, y) можно вы-
числить схемой размера O(2
log m
) = O(m). Т.к. необходимо вычислить не более m функций, A
y , r
i
,...,r
m
имеет размер
схемы O(m
2
) + size(C).
С использованием данной леммы можно доказать следующую теорему.
Теорема (Nisan-Wigderson). Если существует L ∈ DTIME(2
O(n)
) такой, что для всех достаточно больших n
H(L
n
) ≥ 2
εn
, ε > 0, тогда для всех m существует G
m
: {0, 1}
O(log m)
→ {0, 1}
m
являющийся (m
2
, 1/m) псевдослу-
чайным генератором вычислимым за время, полиномиальноеот m.
Доказательство.
Анализ
4.1.2 Полиномиальный алгоритм распознавания простоты числа
Проблема проверки простоты натурального числа является одной из древнейших и классических задач теории чисел.
Неэффективные тесты (типа решета Эратосфена) были известны еще до нашей эры. С развитием теории алгоритмов
возник вопрос о существовании эффективных (полиномиальных) алгоритмов проверки простоты числа, которые за
полиномиальное от длины входа (dlog ne для числа n, заданного в двоичной системе) проверяют является ли n простым
числом.
Мы описываем ниже модифицированный алгоритм проверки простоты, предложенный в 2002 г. тремя индийски-
ми математиками. Более точно мы следуем за статьей M. Agrawal, N. Kayal, N. Saxena, Primes is in P, Annals of
Mathematics, 2004, v. 160, pp. 781–793.
Некоторые определения и обозначения
Определение 67 Через gcd(a, n) обозначим наибольший общий делитель (НОД) чисел a и n.
Определение 68 Пусть gcd(r, n) = 1. Тогда o
r
(n) — порядок n по модулю r: минимальное k такое, что
n
k
= 1 (mo d r).
Через φ(r) обозначается функция Эйлера, равная числу взаимно простых с r чисел, не превосходящих r.
Идея и основная лемма
Лемма 25 Пусть a — целое число, n — натуральное, n ≥ 2 и gcd(a, n) = 1. Тогда n простое тогда и только
тогда, когда
(X + a)
n
= X
n
+ a (mod n).
Доказательство Заметим, что коэффициент при X
i
в (X + a)
n
− (X
n
+ a) равен
n
i
a
n−i
при 0 < i < n.
Рассмотрим два случая.
1. n — простое. Тогда
n
i
mod n = 0 и все коэффициенты равны нулю.
2. n — составное. Рассмотрим его простой делитель q и пусть k — максимальная степень такая, что n делится на
q
k
. Тогда q
k
не является делителем
n
q
и взаимно просто с a
n−q
(упражнение 1). Следовательно, коэффициент при X
q
не равен нулю (mod n). 2
116

Алгоритм 32 Полиномиальный алгоритм для проверки простоты
Вход: целое n > 1.
1. if (n = a
b
для a ∈ N и b > 1), return 0.
2. найти наименьшее r такое, что o
r
(n) > log
2
n.
3. for a = 1 to r do if 1 < gcd(a, n) < n return 0.
4. if n ≤ r, return 1.
5. for a = 1 to b
p
φ(r) log nc do if (X + a)
n
6= X
n
+ a (mod X
r
− 1, n), return 0.
6. return 1.
Время работы
Покажем, что алгоритм 32 полиномиален.
Приведем без доказательства известный факт из теории чисел:
Лемма 26 Обозначим через LCM(m) наименьшее общее кратное первых m натуральных чисел. Тогда LCM(m)
не меньше 2
m
при m ≥ 7.
Лемма 27 Существует r ≤ max(3, dlog
5
ne) такое, что o
r
(n) > log
2
n.
Доказательство При n = 2 значение r = 3 тривиально удовлетворяет всем условиям. Предположим, что n > 2.
Тогда dlog
5
ne > 10 и мы можем воспользоваться леммой 26.
Пусть r
1
, r
2
, ... , r
t
— все числа такие, что либо o
r
i
(n) ≤ log
2
n, либо r
i
является делителем n. Каждое из этих чисел
должно делить произведение
n ·
blog
2
nc
Y
i=1
(n
i
− 1) < n
log
4
n
≤ 2
log
5
n
.
По лемме наименьшее общее кратное первых dlog
5
ne натуральных чисел не меньше 2
dlog
5
ne
и, следовательно, су-
ществует число s ≤ dlog
5
ne такое, что s /∈ {r
1
, r
2
, . . . , r
t
}. Если gcd(s, n) = 1, то все доказано. Если же gcd(s, n) > 1,
то, поскольку s не делит n, и s ∈ {r
1
, r
2
, . . . , r
t
} выполнено r =
s
gcd(s,n)
/∈ {r
1
, r
2
, . . . , r
t
} и, следовательно, o
r
(n) >
log
2
n.
2
Упражнение 58 Покажите, что шаг 1 можно выполнить за полиномиальное время.
Из леммы 27 вытекает, что шаги 2, 3, 4 и 5 выполнимы за полиномиальное время.
Отсюда получаем:
Теорема 30 Алгоритм 32 полиномиален.
Упражнение 59 Для каких n можно исключить шаг 4 из алгоритма 32?
Корректность
То, что для простого n алгоритм выдает 1 — очевидно следует из описания алгоритма.
Нам надо доказать, что если алгоритм выдает 1, то n является простым числом (т.е. если число составное, то сра-
ботает какая-либо из «проверок» алгоритма, и алгоритм вернет 0).
Итак, допустим, число n — составное, но шаги 1 и 3 его не выявили. Рассмотрим последний «фильтр» — шаг 5
внимательно.
Поскольку o
r
(n) > 1 (кстати, почему?), должно существовать простое p, делящее n такое, что o
r
(p) > 1 (заметим,
что если n-простое, то p = n). Зафиксируем числа p и n. Пусть также l = b
p
φ(r) log nc.
Рассмотрим самый содержательный шаг алгоритма, шаг 5. На шаге 5 алгоритма проверяется l уравнений. Посколь-
ку по нашему предположению алгоритм не выдает 0, то для любого 0 ≤ a ≤ l
(X + a)
n
= X
n
+ a (mod X
r
− 1, n),
откуда следует
(X + a)
n
= X
n
+ a (mod X
r
− 1, p).
С другой стороны, из основной леммы 25 следует, что
(X + a)
p
= X
p
+ a (mod X
r
− 1, p)
117

Из двух предыдущих равенств следует, что
(X + a)
n/p
= X
n/p
+ a (mod X
r
− 1, p)
Упражнение 60 Докажите этот факт используя тождество
(X + a)
p
= X
p
+ a
p
mod p.
Определение 69 Для полинома f (X) натуральное число m принадлежит множеству I[f(X)], если
f(X)
m
= f(X
m
) (mod X
r
− 1, p)
Лемма 28 Множество I[f (X)] замкнуто относительно умножения. Если m
1
, m
2
∈ I[f(X)], то m
1
· m
2
∈
I[f (X)].
Доказательство Поскольку m
1
∈ I[f(X)], то
[f(X)]
m
1
·m
2
= [f(X
m
1
)]
m
2
( mod X
r
− 1, p).
Поскольку m
2
∈ I[f(X)], то заменяя X на X
m
1
, имеем:
[f(X
m
1
)]
m
2
= f(X
m
1
·m
2
)( mod X
m
1
r
− 1, p) =
f(X
m
1
·m
2
)( mod X
r
− 1, p),
поскольку X
r
− 1 является делителем многочлена X
m·r
− 1.
Из этих двух соотношений получаем:
[f(X)]
m
1
·m
2
= f(X
m
1
·m
2
)( mod X
r
− 1, p).
2
Лемма 29 Если m ∈ I[f(X)] и m ∈ I[g(X)], то m ∈ I[f(X) · g(X)].
Доказательство Имеем:
[f(X) · g(X)]
m
= [f(X)]
m
· [g(X)]
m
=
f(X
m
) · g(X
m
)( mod X
r
− 1, p).
Определим два множества:
I = {(
n
p
)
i
· p
j
| i, j ≥ 0},
P = {(
l
Y
a=0
(X + a)
e
a
| e
a
≥ 0}.
2
Простым следствием лемм 28 и 29 является:
Лемма 30 Для любого m ∈ I выполнено m ∈ I[P].
Рассмотрим теперь две группы, основанные на введенных множествах. Пусть G обозначает группу всех вычетов
чисел из I по модулю r. Пусть t = |G|. G является подгруппой мультипликативной группы Z
∗
r
, поскольку, как отмечено
выше, gcd(n, r) = gcd(p, r) = 1. Группа G порождается элементами n и p по модулю r и, поскольку, o
r
(n) > log
2
n, то
t > log
2
n.
Пусть Q
r
(X) — r-й циклотомический полином в поле F
p
. Полином Q
r
(X) является делителем X
r
−1 и расклады-
вается на неприводимые множители степени o
r
(p) [?]. Пусть h(X) такой неприводимый многочлен в F
p
степени o
r
(p).
Такой многочлен, как отмечено выше, всегда существует, если gcd(p, r) > 1. Пусть H обозначает группу всех вычетов
полиномов из P по модулю h(X) и p.
Группа H порождается элементами X, X + 1, X + 2, .. . , X + l в поле F = F
p
[X]/(h(X)) и является подгруппой
группы F .
Следующие две леммы дают нижнюю и верхнюю оценку размера группы H.
Лемма 31 |H| ≥
t+l
t−1
.
118

Доказательство Доказательство. Заметим сначала, что поскольку h(X) является делителем циклотомического по-
линома Q
r
(X), то X — примитивный r-й корень из единицы в F .
Покажем теперь, что любые два различных полинома в множестве P степени меньше, чем t соответствуют различ-
ным элементам H. Пусть f(X) и g(X) — такие полиномы из P . Предположим f (X) = g(X) в поле F и пусть m ∈ I.
Имеем: [f(X)]
m
= [g(X)]
m
в F . Поскольку m ∈ I[f], m ∈ I[g], и h(X) является делителем X
r
− 1, получаем, что в
поле F выполнено:
f(X
m
) = g(X
m
).
Отсюда вытекает, что X
m
является корнем многочлена Q(Y ) = f(Y ) − g(Y ) для любого m ∈ G. Поскольку
(m, r) = 1 (т.к. G — подгруппа Z
∗
r
) любое такое X
m
является примитивным r-м корнем из единицы. Следовательно,
должно быть |G| = t различных корней многочлена Q(Y ) в поле F . Однако, степень Q(Y ) меньше t в силу выбора f и
g. Это противоречие доказывает, что f(X) 6= g(X) в F .
Заметим, что i 6= j в F
p
для 1 ≤ i 6= j ≤ l, поскольку l = b
p
φ(r) log nc <
√
r log n < r, и p > r. Значит все
элементы X, X + 1, X + 2, . . ., X + l различны в поле F . Также, поскольку степень h больше единицы, X + a 6= 0 в F
для всех a, 0 ≤ a ≤ l. Значит, существует не менее l + 1 различных полиномов первой степени в H. Отсюда вытекает,
что существует не менее
t+l
t−1
различных полиномов степени < t в H. 2
Лемма 32 Если n не является степенью p, то
|H| ≤ n
√
t
.
Доказательство Рассмотрим следующее подмножество множества I:
I
1
= {(
n
p
)
i
· p
j
0 ≤ i, j ≤ b
√
tc}.
если n не является степенью простого, то |I
1
| ≥ (b
√
tc + 1)
2
> t. Поскольку |G| = t, по крайней мере два числа из
I
1
должны быть равны по модулю r. пусть это будут m
1
и m
2
и m
1
> m
2
. Имеем:
X
m
1
= X
m
2
( mod X
r
− 1).
Пусть f(X) ∈ P . Тогда
[f(X)]
m
1
= f(X
m
1
) ( mod X
r
− 1, p) =
f(X
m
2
) ( mod X
r
− 1, p) =
[f(X)]
m
2
( mod X
r
− 1, p).
Отсюда вытекает, что в поле F
[f(X)]
m
1
= [f(X)]
m
2
.
Следовательно, f(X) ∈ H является корнем многочлена Q
1
(Y ) = Y
m
1
−Y
m
2
в поле F . Поскольку f(X) произвольный
элемент H, многочлен Q
1
(Y ) имеет не менее |H| различных корней в поле F . Однако, степень многочлена Q
1
(Y ) равна
m
1
≤ (
n
p
· p)
b
√
tc
≤ n
b
√
tc
.
Это доказывает, что |H| ≤ n
b
√
tc
. 2
Завершающей является лемма, основанная на сравнении нижней и верхней оценок из лемм 31 и 32.
Лемма 33 Если алгоритм выдает ПРОСТОЕ, то n является простым числом.
Доказательство Предположим алгоритм выдает ПРОСТОЕ. Из леммы 29 вытекает, что для t = |G|и l = b
p
φ(r) log nc:
|H| ≥
t + l
t − 1
≥
l + 1 + b
√
t log nc
b
√
t log nc
( поскольку t >
√
t log n)
≥
2b
√
t log nc + 1
b
√
t log nc
( поскольку l = b
p
φ(r) log nc ≥ b
√
t log nc)
> 2
b
√
t log nc+1
( поскольку b
√
t log nc > blog
2
nc ≥ 1)
119

≥ n
√
t
.
По лемме 32, |H| ≤ n
√
t
если n не степень p. Следовательно, n = p
k
для некоторого k > 0. Если k > 1, то алгоритм
выдаст СОСТАВНОЕ на шаге 1. Значит, n = p. 2
Окончательно получаем:
Теорема 31 Если n — простое ⇔ алгоритм всегда выдает ПРОСТОЕ.
4.2 Элементы криптографии с открытым ключом
4.2.1 Односторонние функции
Центральным понятием «новой криптографии» является понятие односторонней функции.
Определение 70 Односторонней называется функция F : X → Y , обладающая двумя свойствами:
1. существует полиномиальный алгоритм вычисления значений F (x);
2. не существует полиномиального алгоритма инвертирования функции F (т.е. вычисления обратной
функции — решения уравнения F (x) = y относительно x).
Это не совсем формальное определение. Более формально свойство 2 формулируется так: любая полиномиальная
вероятностная машина Тьюринга T по y ∈ Y может найти x из уравнения F (x) = y лишь с пренебрежимо малой
вероятностью (меньше
1
p(n)
для любого полинома p(n), где n — длина входа), т.е.
P {F (T (F (x))) = F (x)} <
1
p(n)
.
Здесь вероятность берется по равномерно распределенному x ∈ X и случайным битам вероятностного алгоритма T .
При этом рассматривается дополнительное ограничение на мощность X: считается, что она не превосходит некоторого
полинома от мощности Y .
Вопрос о существовании односторонних функций пока открыт и является одним из центральных в теоретической
криптографии и теории сложности. Однако, есть функции, которые предположительно являются односторонними. Од-
на из них — дискретный логарифм (уже упоминавшийся в разделе 1).
4.2.2 Дискретный логарифм. Обмен ключами.
Напомним некоторые сведения из алгебры. Для любого простого числа p множество Z
p
= {0, 1, . . . , p − 1} является
полем с операциями умножения и сложения по модулю p. Известно, что Z
∗
p
= Z
p
− {0} образует циклическую группу
по умножению. Любой порождающий элемент этой группы называется примитивным элементом.
Задача 31 «Дискретный логарифм»
Даны примитивный элемент g, b 6= 0, простое число p. Найти x такое, что
g
x
= b mo d p.
Опишем сейчас применение дискретного логарифма для задачи формирования общего секретного ключа двумя
пользователями (задача 32), связанными открытым (для противника) каналом связи.
Задача 32 «Формирование секретного ключа»
Абоненты A и B взаимодействуют по открытому каналу связи. Могут ли они, не имея вначале никакой
секретной информации, организовать обмен так, чтобы в конце у них появлялся общий секретный ключ.
Предполагается, что пассивный противник может перехватить все сообщения, которыми они обменива-
ются.
Диффи и Хеллман предложили решать эту задачу с помощью дискретного логарифма (алгоритм 33).
Задача А. Противник знает p, a, a
X
A
, a
X
B
, но не знает X
A
и X
B
, и хочет узнать a
X
A
X
B
.
Гипотеза Диффи-Хеллмана. Задача А — вычислительно трудна.
В настоящее время нет алгоритмов решения задачи А, более эффективных чем дискретное логарифмирование. А
это — трудная математическая задача.
Дискретный логарифм обладает интересным свойством: если эта функция сложна в худшем случае, то сложна
и в среднем. Доказательство этого свойства простое и мы приведем его сейчас, предварительно дав более точную
формулировку.
120
