Кузьмин С.И. Методы научных исследований в технических задачах
Подождите немного. Документ загружается.


31
Четвертый центральный момент
4
μ
участвует в вычис-
лении коэффициента эксцесса распределения случайной ве-
личины
2
γ
(рис. 2.4.):
3
4
4
2
−=
x
σ
μ
γ
.
Рис. 2.4. Плотность распределения случайной
величины
x
с различными коэффициентами эксцесса
и одинаковыми
1
μ
и
2
μ
Кроме моментов функции распределения характеризуют-
ся отдельными значениями - квантилями. Квантилем
p
x
рас-
пределения случайной величины
x
с функцией распределе-
ния
()
xF
называется такое значение случайной величины
x
,
для которой выполняется условие:
(
)
pxxP
p
=
<
.
Например, квантиль
5,0
x
называется медианой и рассека-
ет площадь между кривой плотности вероятности и осью
абсцисс пополам (рис. 2.5).

32
Рис. 2.5. Графическое представление медианы
распределения
Для характеристики случайной величины
x
часто ис-
пользуют понятие о нормированной случайной величине -
0
x
:
()
xx
mxx
σ
/
0
−=
, тогда
0
0.
=
x
m
и
1
2
0.
=
x
σ
.
2.2. Свойства математического ожидания и дисперсии
Математическое ожидание (обозначается
()
xM
или
x
m
)
дискретной случайной величины
x
равно:
Mx x p
ii
i
n
()=⋅
=
∑
1
,
где
i
p
- вероятность случайной величины
i
x
.
Для непрерывных случайных величин математическое
ожидание выражается интегралом:
Mx m xf xdx
x
() ()==
−
∞
+
∞
∫
.
Математическое ожидание и дисперсия обладают сле-
дующими свойствами:
1. Математическое ожидание неслучайной величины
с
равно значению этой величины:
(
)
ссМ
=
;
33
2. Неслучайную величину можно вынести за знак мате-
матического ожидания:
(
)
(
)
xcMcxM
=
.
3. Математическое ожидание суммы случайных величин
равно сумме математических ожиданий этих случай-
ных величин:
()
(
)
(
)
(
)()
ii
xMxMxMxMxxxxM ++
+
+
=
++++ .......
321321
.
4. Математическое ожидание произведения случайных
величин равно произведению математических ожида-
ний этих случайных величин:
()
(
)
(
)
(
)()
ii
xMxMxMxMxxxxM *...****....***
321321
=
.
1. Дисперсия неслучайной величины
с
равна 0:
(
)
0
2
== cD
c
σ
.
2. Неслучайную величину
с можно выносить за знак дис-
персии; возведя ее в квадрат:
(
)
(
)
222
x
cxDccxD
σ
==
.
3. Дисперсия случайной величины
x
равна математиче-
скому ожиданию квадрата случайной величины минус
квадрат ее математического ожидания
(
)
(
)
222
xx
mxMxD −==
σ
.
4. Дисперсия суммы независимых случайных величин
равна сумме дисперсий этих величин:
()
(
)
(
)
(
)
22
2
2
12121
..........
xixxii
xDxDxDxxxD
σσσ
+++=+++=+++
2.3. Виды распределения случайной величины
Распределение случайной величины в некотором интер-
вале возможных значений может быть произвольным. В
практическом использовании теории вероятности применя-
ются только наиболее изученные законы распределения. К
ним относятся: равномерное, биноминальное (Бернулли),
нормальное, экспоненциальное.
34
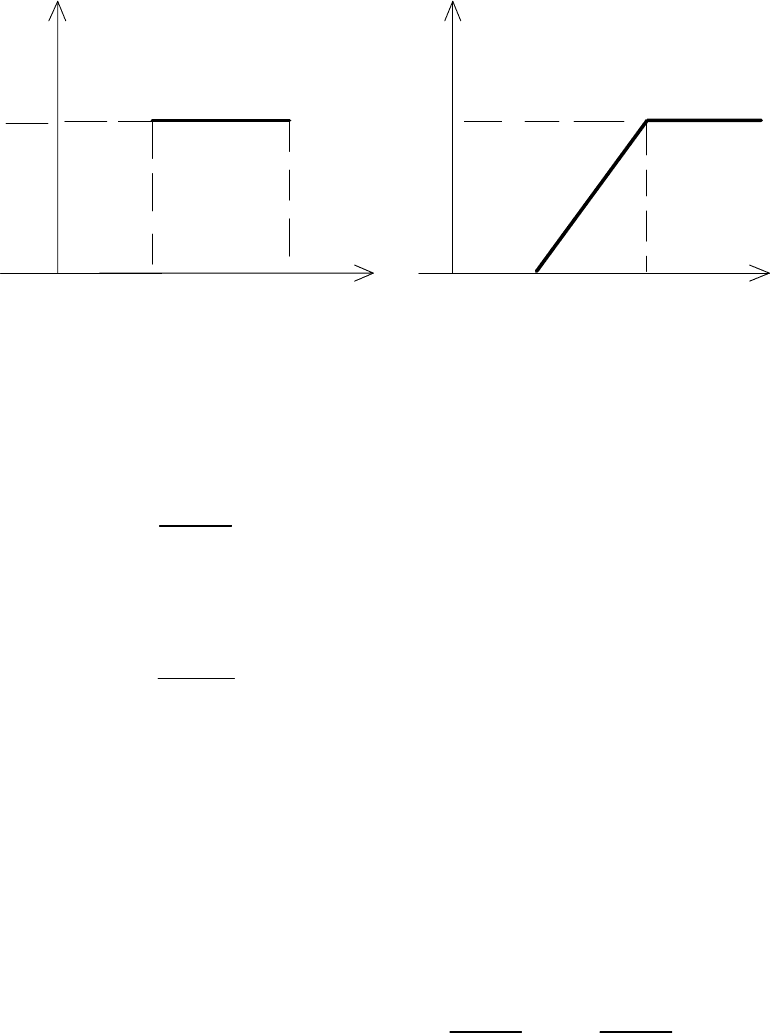
2.3.1. Равномерное распределение
Равномерным, называется распределение, для которого
плотность вероятности постоянна в определенном интервале
значений случайной величины и равна нулю вне этого интер-
вала (рис. 2.6.).
с
ba
=
−
1
f(x)
x
a
1
b
2
a
1
b
2
x
F(x)
1.0
0 0
а) б)
Рис. 2.6. Графики плотности вероятности
а) и функции б) равномерного распределения
fx
ba
axb
xa xb
()=
−
≤≤
<>
⎧
⎨
⎪
⎩
⎪
1
0
при
при
Fx
xa
ba
axb
xa
xb
()=
−
−
≤≤
<
>
⎧
⎨
⎪
⎪
⎩
⎪
⎪
при
при
при
0
1
Математическое ожидание случайной величины
x
, рав-
номерно распределенной в интервале (
ba,
) равно:
mxfxdx
x
ba
dx
ab
x
a
b
a
b
==
−
=
+
∫∫
()
2
.

35
Дисперсия
2
x
σ
равна:
∫∫
−
=
+
−
−
=−=
b
a
b
a
x
ab
dx
ba
x
ab
dxmxxf
12
)(
)
2
(
1
))((
2
222
σ
.
Коэффициент асимметрии
3
γ
:
0
4
)
2
()
2
(
)(
1
)
2
(
1
)()(
44
3
3
3
3
3
3
3
3
=
−
−
−
⋅
−
=
=
+
−
−
=
=
==
∫∫
baab
ab
dx
ba
x
ab
dxxfmx
x
x
b
a
x
b
a
x
x
σ
σσσ
μ
γ
.
Коэффициент эксцесса
4
γ
:
γμσ
44
4
3=−
x
;
∫
−
=
+
−
−
=
b
a
ab
dx
ba
x
ab 80
)(
)
2
(
1
4
4
4
μ
;
2,13
)(80
14)(
4
44
4
−=−
−⋅
⋅−
=
ab
ab
γ
.
Медиана случайной величины х будет равна математиче-
скому ожиданию:
2
5,0
ba
mx
x
+
==
2.3.2. Биноминальное распределение (Бернулли)
Если осуществление некоторого события происходит с
постоянной вероятностью
p
и эта вероятность не зависит от
результата предыдущих испытаний, то вероятность наступ-
ления m событий при n испытаниях (m и n - целые числа) вы-
числяется по формуле, предложенной швейцарским матема-
тиком Я. Бернулли:
mnm
n
pp
m
mnnn
mP
−
−
+
−
−
= )1(
!
)1)......(1(
)(
36
и такое распределение называется биноминальным или Бер-
нулли.
Наиболее распространенным примером биноминального
распределения является бросание монеты. В этом случае
5,0=p
. Естественно, что биноминальное распределение от-
носится к дискретным величинам.
2.3.3. Нормальное распределение случайных величин
Случайная величина
x
называется распределенной по
нормальному закону, если ее плотность распределения имеет
вид:
fx EXP
xm
x
x
x
x
()
()
,=−
−
⎛
⎝
⎜
⎜
⎞
⎠
⎟
⎟
−∞ < < +∞
1
2
2
2
2
2
πσ
σ
где
x
m
и
2
x
σ
- математическое ожидание и дисперсия
случайной величины
x
.
Функция распределения:
dxexF
x
x
mx
x
∫
∞+
∞−
−
−
=
2
2
2
)(
2
2
1
)(
σ
πσ
.
В природе множество событий происходит случайно,
вследствие воздействия на них большого числа относительно
«равновеликих» независимых возмущений. У таких явлений
закон распределения близок к нормальному. График плотно-
сти нормального распределения называется нормальной кри-
вой или кривой Гаусса.

37
f(x)
x
0
x
m
1
x
Рис. 2.7. График плотности нормального
распределения
Центральные моменты
(
)
x
s
μ
случайной величины, вероят-
ность которой имеет нормальное распределение, определя-
ются следующим образом [3]:
∫
∞
∞−
−
−
−=−= dxe)mx(
2
1
dx)x(f)mx(]x[
2
2
2
)mx(
ss
s
σ
πσ
μ
,
или после преобразований получается:
(
)
2
2
1
−
−=
ss
s
μσμ
,
где
s
= 0,1,2,3….
Эта формула представляет собой простое рекуррентное со-
отношение, позволяющее выражать центральные моменты
более высоких четных порядков через центральные моменты
более низких. В частности, учитывая, что для любой случай-
ной величины
0
μ
=1, получается:
2
μ
=
2
σ
;
4
μ
=3
2
σ
;
6
μ
=3⋅5
2
σ
и т.д.
Следовательно, эксцесс
нормального распределения равен
нулю:
03
4
4
2
=−=
σ
μ
γ
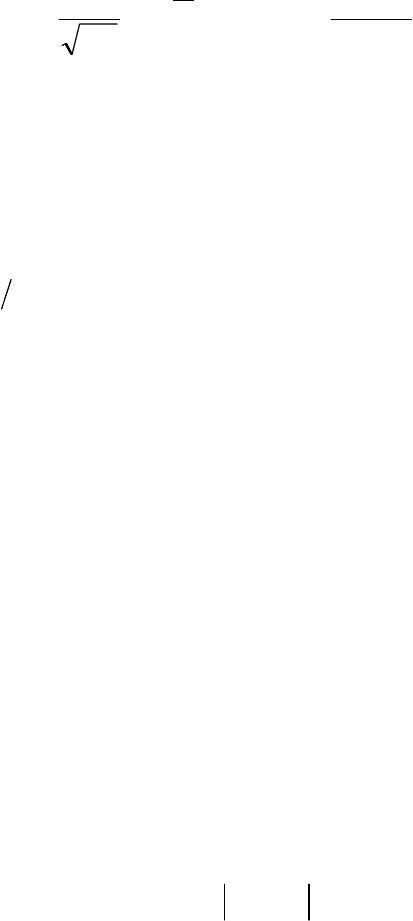
38
Нормальное распределение для нормированной случай-
ной величины называется стандартным. Его функция распре-
деления имеет вид:
x
x
x
x
mx
xdxeF
σ
π
−
==
∫
∞−
−
0
2
0
,
2
1
2
.
Вероятность попадания случайной величины
x
со стан-
дартным нормальным распределением в интервал
()
21
xx −
вычисляется через
0
F
:
()
(
)
(
)
(
)()
121020201
xФxФxFxFxxxP
−
=
−
=
≤≤
,
где
() ()
21
0
−= xFxФ
- Функция Лапласа.
Если принять, что
1
x
и
2
x
симметричны относительно
математического ожидания
x
m
, то функцию Лапласа можно
использовать для исключения грубой ошибки (результат из-
мерений, содержащий заведомый промах и, как следствие,
необъективно оценивающий физический эффект) в опытах.
Допуская, что результаты измерений содержат случай-
ные ошибки, величина которых подчиняется нормальному
закону, проверяют условие попадания результата опыта в за-
ранее назначенный интервал. Величину интервала удобно
привязывать к стандартному отклонению
σ
.
Абсолютное отклонение
x
Δ
результата измерения (слу-
чайная величина)
x
от математического ожидания
x
m
со-
ставляет ошибку измерения:
x
mxx −=Δ
.
Требуется найти вероятность того, что абсолютные от-
клонения случайной величины не превысит некоторого за-
данного числа
ε
:
()
(
)
ε
ε
ε
+
≤
≤
−
=
≤Δ
xx
mxmPxP
.
Для нормированной случайной величины
0=
x
m
:
()( )
(
)
(
)()
ε
ε
ε
ε
ε
ε
ФФФxPxP 2
0
=
−
−
+
=
+
≤
≤−=≤Δ

39
Для случайной величины, имеющей нормальное распре-
деление с параметрами
x
m
и
x
σ
:
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
≤Δ=≤Δ
xx
ФxPxP
σ
ε
σ
ε
ε
2
0
Вводя обозначение
k=
σ
ε
, получаются соотношения:
()
(
)
kФkxP
x
2=≤Δ
σ
;
(
)
(
)
628,012 =
=
≤
Δ
ФxP
x
σ
;
()()
954,0222
=
=≤Δ ФxP
x
σ
;
(
)()
9973,0323 =
=
≤
Δ
ФxP
x
σ
Таким образом, вероятность появления отклонения
больше чем утроенный стандарт (среднеквадратичное откло-
нение) составляет всего 0,27% , что считается практически
невозможным и позволяет сделать вывод о наличии в резуль-
тате измерения грубой ошибки.
Основные характеристики нормального распределения
x
m
и
x
σ
определяются из функции распределения. График
плотности нормального распределения имеет экстремум в
точке
x
m
и две точки перегиба
xx
mx
σ
−
=
1
и
xx
mx
σ
+=
2
со
значением функции
e⋅
πσ
21
.
Изменение математического ожидания приводит к сдви-
гу кривой вдоль оси
x
, а с возрастанием дисперсии макси-
мальная ордината нормальной кривой убывает и сам график
становится более пологим (рис. 2.8.).
f
(x)
x
а
)
x
f
(x)
б
)
σ
x1
σ
x2
σ
x1
<
σ
x2
X
1
x
2
x
3
m
x1
<0 m
x2
=0 m
x3
>0
Рис. 2.8. Изменение графика функции плотности нор-
мального распределения при изменении ее численных ха-
рактеристик а)
x
m
; б)
x
σ
40
Коэффициенты асимметрии и эксцесса нормального рас-
пределения равны нулю. Если искусственно ввести в функ-
цию нормального распределения изменения связанные с
0
1
≠
γ
и
0
2
≠
γ
, то это вызовет следующие преобразования
(рис. 2.9).
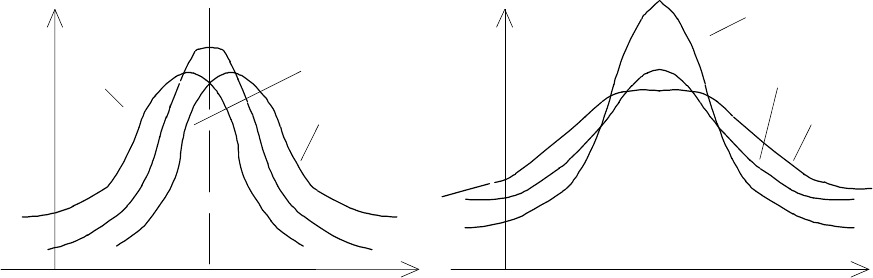
Асимметрия вытягивает (удлиняет) одну из половин кри-
вой (относительно
x
m
) по оси
x
.
Эксцесс изменяет «крутость» кривой распределения по
отношению к стандартной. При
2
γ
>0 подъем вершины уве-
личивается, и наоборот если
2
γ
<0, то кривая имеет более
плоскую и низкую вершину.
f(x)
x
m
x
γ
1
<0
x
f(x)
а
)
б
)
γ
1
=0
γ
1
>0
γ
2
>0
γ
2
=0
γ
2
<0
Рис. 2.9. График нормального распределения плотности
вероятности с ненулевыми значениями коэффициентов
асимметрии а) и эксцесса б) при одинаковых
x
m
и
x
σ
Коэффициенты асимметрии и эксцесса можно использо-
вать для сравнения близости реального распределения к нор-
мальному.
2.3.4. Распределение
2
χ
(хи - квадрат)
Если имеется
n
результатов независимых испытаний над
случайной нормальной величиной
x
с математическим ожи-
