Кузьмин С.И. Методы научных исследований в технических задачах

Подождите немного. Документ загружается.

вится возможным замена исследуемой системы

на нето-

ждественную ей систему

, аналогичную ей только по ис-

следуемым характеристикам. Новая система

является

моделью системы

. Модель характеризуется как мыслен-

но представляемая или материально реализуемая система,

которая, отражая или воспроизводя объект исследования,

способна дать новую информацию об этом объекте.

Различают концептуальные, аналоговые (логические) и

кибернетические (функциональные) модели [2]:

- концептуальные модели строятся с помощью аппарата

математической логики, на основе наблюдения за объектом в

процессе его функционирования.

- аналоговые

системы применяют, если явления, проис-

ходящие в разных системах, формально описываются одина-

ковыми дифференциальными уравнениями. В этом случае

можно говорить о том, что одна система является моделью –

аналогом другой системы.

В современной науке резко возросла роль функцио-

нальных моделей, имитирующих только поведение оригина-

ла. Сложная материальная система рассматривается как

единство

трёх объективных начал: вещества, структуры и

функциональных связей со средой.

Обобщённым абстрактным образом функциональной мо-

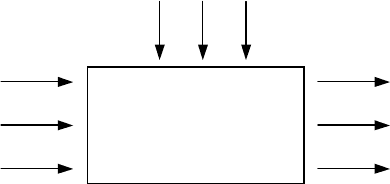
дели является «чёрный ящик» (рис.1.1).

Случайные факторы

Входные Черный Целевые

факторы ящик функции

Рис. 1.1. Схема функциональной модели типа

«черный ящик»

«Чёрный ящик» – система, внутреннее устройство кото-

рой не известно наблюдателю, но он может исследовать вхо-

ды

и выходы

этой системы. Соответственно функцио-

нальная модель «чёрного ящика» должна соответствовать

изучаемой системе по входам и выходам. Такой подход по-

зволяет отвлечься от сложных явлений, происходящих в сис-

теме

и значительно ускорить решение практических за-

дач.

При проведении исследований, важно определить к ка-

кому классу относится данная система: детерминированная

(причинная) или стохастическая (вероятностная).

Развитие детерминированной системы полностью обу-

словлено определенными причинами и не подвержено слу-

чайностями. Изменение одного фактора

на некоторую ве-

личину

XΔ

всегда вызывает изменение выхода

на строго

определенную величину

В стохастических системах изменение фактора

на

XΔ

, вызывает изменение выхода

на величину

)(

+Δ

где

)(

случайная величина.

К стохастическим системам относятся большинство тех-

нических и технологических задач, протекающих в реальных

условиях. Это является следствием, прежде всего, непрерыв-

но меняющейся обстановки, воздействием на процессы мно-

жества факторов, влияние которых устранить практически не

возможно.

Известный теоретик науки Ф. Франк обращает внимание

на существование двух различных стохастических систем [3].

В первом типе систем наличиствуют причинные связи, а не-

определенность в результате (выходе системы) обусловлены

разбросом начальных условий, от которых начинается функ-

ционирование системы. Примером такого типа систем явля-

ется стрельба по мишени. С одной стороны процесс движе-

ния материальной частицы (пули) при выстреле описывается

законами ньютоновской механики и можно точно вычислить

место попадания пули в мишень, зная начальные условия:

импульс, массу пули, расстояние до мишени. С другой сто-

роны практическая реализация выстрелов из одного и того же

оружий при

одних и тех же условиях показывает наличие

разброса точек попадания пуль в мишень, что как раз и обу-

славливается невозможностью обеспечения одинаковости

всех начальных условий в реальности, по сравнению с теоре-

тической моделью. Однако если последовательно уменьшать

разброс начальных условий относительно базовых, то и раз-

брос неточностей в попадании пули

в центр мишени должен

уменьшаться и стремится к нулю, то есть система может пе-

рейти из стохастической в детерминированную. Таким обра-

зом, такой тип стохастических систем характеризуется воз-

можностью влияния на конечный результат путем изменения

начальных условий.

В других системах этого не происходит в силу независи-

мости (непредсказуемости) результата от начальных

условий.

В таких случаях можно говорить только о статистических

показателях, стремящихся к какому-либо значению при мно-

гократном воспроизведении процесса. Так, например, при

бросании монеты выпадание «решки» или «орла» не зависит

от разброса начальных условий и изменение начального раз-

броса (дисперсии) никак не влияет на результат в конкретном

единичном подбрасывании.

Но при этом проявляется зако-

номерность стремления общего количества выпавших сторон

монеты к равному соотношению с ростом числа подбрасыва-

ний.

Существует целый класс систем, которые, не смотря на

случайный характер величины отклика, можно рассматривать

как статистически устойчивые и прогнозировать их поведе-

ние с определенной надежностью (вероятностью). Степень

доверия к поведению стохастических систем определяется

законами теории вероятности.

Кроме того, практически все технические системы отно-

сятся к стохастическим уже в силу того, что значения входов

и выходов определяется измерением. А процесс измерения

несет в себе элементы неопределенности и порой единствен-

ным способом оценить эту

неопределенность является при-

менение методов теории вероятности и математической ста-

тистики.

Некоторые положения теории вероятности и математиче-

ской статистики рассмотрены в следующих главах.

2. Характеристики случайных величин

2.1. Основные понятия

Под случайным событием понимается факт, который в

результате испытания может произойти или не произойти

[4,5]. Мерой объективной возможности осуществления слу-

чайного

события

является вероятность

{

}

. Пределы из-

менения вероятности от нуля (невероятное события) до еди-

ницы (достоверное событие):

{

}

(

)

≤

Если в серии из

испытаний некоторое ожидаемое со-

бытие происходит

раз, а

раз не происходит, то отноше-

ние

)( nmn +

рассматривается как вероятность появления

благоприятного (ожидаемого) события:

{}

соответственно вероятность противоположного события со-

ставит :

{}

Здесь важно, что бы события были статистически устой-

чивыми и независимыми.

Под статистической устойчивостью понимают свойство

многократного (теоретически неограниченного) воспроизве-

дения одного и того же события в одинаковых (или как гово-

рят статистически однородных) условиях. Наиболее распро-

страненным и важным примером таких событий является

процесс изменения какой-либо величины, проводимый оди

наковым методом.

Случайное событие может быть и неопределенным, то

есть таким которое невозможно воспроизвести в одинаковых

условиях. Например, утверждение: «Московский «Спартак»

станет чемпионом страны в следующем сезоне» хотя и слу-

чайное, но неопределенное событие, так как с течением вре-

мени изменяется состав команды, участвующие клубы, трав-

мы и спортивная форма

футболистов, погодные условия и

т.д. Вообще говоря, формированию статической устойчиво-

сти не мешает воздействие других случайных событий. Так

глубина промерзания грунта - статистически устойчивая ве-

личина, но каждый год она определяется изменчивыми слу-

чайными метеорологическими условиями.

Случайные события

AAА ,...,,

, называются независи-

мыми, если вероятность появления любого из них не зависит

от появления или не появления любого из остальных.

Поведение статически устойчивых случайных событий

изучает теория вероятности и математическая статистика.

Развитие теории вероятности основывается на аксиомах и

теоремах сформулированных и доказанных отечественным

ученым А.И. Колмогоровым в 30-х годах 20-го

века. Вот не-

которые из них:

-вероятность появления случайного события

является

положительным числом:

{

}

>0;

-вероятность достоверного события равна единице, а ве-

роятность невозможного события равна нулю;

-вероятность наступления хотя бы одного из нескольких

несовместных событий

AAА ,...,,

равна сумме вероятностей

этих событий:

{

}

{

}

{

}

{

}

APAPAPAAAP

+ ..........

2121

;

-вероятность произведения нескольких независимых со-

бытий равна произведению вероятностей этих событий:

{

}

{

}

{

}

{

}

APAPAPAAAP *.....***.....**

2121

Если вероятность появления события

меняется от то-

го, происходит другое событие

или нет, то считается, что

событие

зависит от события

Для взаимозависимых событий вероятность произведе-

ния их совместного появления

(

)

ABP

равна произведению

вероятности одного из них на, так называемую, условную ве-

роятность другого, вычисленную при условии, что первое со-

бытие наступило:

(

)

(

)

(

)

PAPABP *=

где

(

)

- условная вероятность события

, т.е. веро-

ятность его появления, определенная при условии, что про-

изошло зависимое событие

И наоборот, если сначала происходит событие

, влияющее

на вероятность появления события

, то:

(

)

(

)

(

)

PBPBAP *=

Сумма вероятностей всех возможных

значений слу-

чайной величины

равна единице:

∑

1)(

Суммарная вероятность распределяется определенным

образом между отдельными значениями величины. Всякое

соотношение, устанавливающее связь между возможным

значением случайной величины и соответствующими веро-

ятностями, называется законом распределения.

Дискретную случайную величину

можно задать веро-

ятностным рядом, указав вероятность

для каждого значе-

ния

...

(x) P

(x) ... P

(x)

Распределение непрерывной случайной величины нельзя

задавать при помощи вероятности отдельных значений. Чис-

ло значений так велико, что для большинства из них вероят-

ность принять эти значения равно нулю. Поэтому для непре-

рывной случайной величины изучается вероятность того, что

в результате опыта значение случайной величины попадет в

некоторую заранее намеченную совокупность

чисел.

Если

случайная величина, а

- произвольное дейст-

вительное число, то вероятность события

является

функцией от

(

)

(

)

aai

yFyyP

и называется функцией распределения случайной величины.

В виде функции распределения можно задавать распре-

деления как непрерывной, так и дискретной случайной вели-

чины. Функция распределения дискретной случайной вели-

чины всегда имеет вид разрывной ступенчатой функции (рис.

2.1.).

Рис. 2.1. Функции распределения дискретной (а) и непре-

рывной (б) случайной величины

Для непрерывной случайной величины ордината функ-

ции распределения, соответствующая значению случайной

величины

, представляет вероятность того, что случайная

величина

окажется меньше

. Разность двух ординат, со-

ответствующих точкам

1+j

дает вероятность того, что

значение случайной величины

лежит в интервале от

до

1+j

(

)

(

)

(

)

jjjj

xFxFxxxP

−

=<<

++ 11

(2.1)

Для непрерывной случайной величины часто используют

понятие плотности распределения

(

)

, являющееся произ-

водной от функции распределения

(

)

(

)

(

)

xFxf

′

Соответственно, вероятность попадания случайной вели-

чины

в интервал

(

)

−

будет составлять:

∫

−==≤≤

)()()()(

1)1(

jjjj

xFxFdxxfxxxP

т.е. будет такой же, что и по определению (см. формулу 2.1.).

Графически плотность распределения, выражается не

разностью ординат, как для

(

)

, а площадью, ограниченной

осью абсцисс, линией функции плотности распределения

()

и ординатами

(рис.2.2).

Рис. 2.2. Плотность распределения непрерывной

случайной величины

Соответственно, вероятность случайного события во всей

области изменения

()

∞

− x

, достоверна:

Px fxdx()().−∞ < < +∞ = =

−

∞

∫

Во многих случаях вместо законов распределения доста-

точно знать основные числовые характеристики, или пара-

метры распределения.

Числовые характеристики случайных величин, выра-

жающие основные особенности называются моментами.

Различают начальные

и центральные

моменты.

Начальные момент к -го порядка определяется по выра-

жениям:

-для дискретной случайной величины (индекс

д ):

mxp

=⋅

∑

, к=1,2....;

-для непрерывной случайной величины (индекс н):

mxfxdx

=⋅

−∞

∞

∑

() .

Соответственно центральные моменты

-го порядка вы-

числяются по формулам:

∑

⋅−=

pmx

)(

;

∑

+∞

∞−

⋅−= dxxfmx

)()(

где

- начальный момент первого порядка.

Начальный момент первого порядка (к=1) называется

математическим ожиданием случайной величины

mMx xp

дд

∑

()

;

mMx xfxdx

нн

−∞

∞

∑

() ()

Математическое ожидание характеризует среднее значе-

ние случайной величины в интервале распределения.

Так как значения случайной величины распределяются

относительно математического ожидания одинаково, то цен-

тральный момент первого порядка равен 0.

Второй центральный момент называется дисперсией

∑

−==

ixi

pmxx

222

)(

σμ

; и

∑

+∞

∞−

−== dxxfmx

)()(

σμ

Корень квадратный из дисперсии называется средним

квадратичным отклонением (и еще стандартом):

2 xx

σσμ

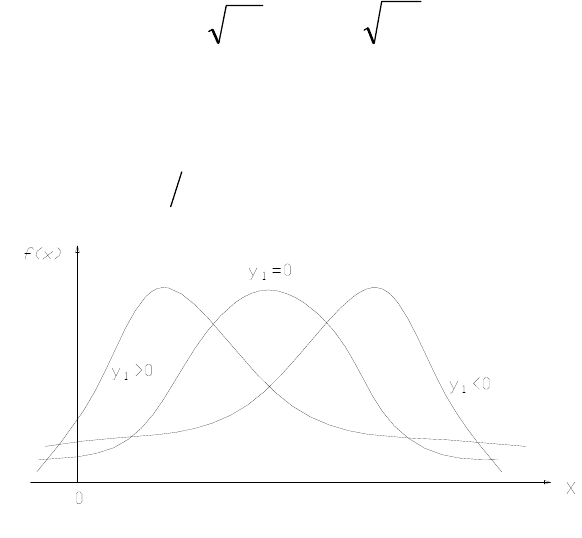
Третий центральный момент

используется в соотно-

шении с кубом стандарта

и служит мерой асимметрии

распределения

31 x

σμγ

(рис. 2.3.).

Рис. 2.3. Плотности распределения случайной вели-

чины

с различными коэффициентами асимметрии и

одинаковыми