Курсовая работа - Анализ и прогнозирование временного ряда развития строительства
Подождите немного. Документ загружается.


102949,78 млрд. руб. А среднегодовой уровень общей площади квартир,
введенных в действие жилищно-строительными кооперативами Тюменской
области в период с 1990-2004 гг. составил, соответственно, 43195,87 м
2
.
Средние показатели изменения уровней ряда представлены: средним
абсолютным приростом, средним темпом роста, средним темпом прироста.
Средний абсолютный прирост представляет собой среднюю из абсолютных
приростов за равные промежутки времени одного периода. Рассчитывается по
формулам:
- по цепным данным об абсолютных приростах за ряд лет можно рассчитать
средний абсолютный прирост как среднюю арифметическую простую:
п
ц
ц
y
y
å
D
D
, (1.14)
где
n
– число степенных абсолютных приростов (
ц
y
D
) в изучаемом
периоде;
- средний абсолютный прирост можно определить на основе накопленного
абсолютного прироста за
n
периодов:
n
yy
n
у
0
D
. (1.15)
Рассчитаем средний абсолютный прирост для исследуемых рядов. Так,
средний годовой абсолютный прирост объема работ, выполненных по договорам
строительного подряда, Тюменской области в период за 1990-2004 гг. составляет
(по формуле 1.15):
D
у
15
93,17042432,110766
= -3977,24 млрд. руб., т. е. в среднем
ежегодно объем строительных работ сокращался на 3977,24 млрд. руб. Средний
годовой абсолютный прирост общей площади квартир, введенных в действие
жилищно-строительными кооперативами Тюменской области за 15 лет
составляет:
D
у
15
1388868772
= 3658,93 м
2
, т. е. в среднем ежегодно общая
площадь квартир увеличивалась на 3658,93 м
2
.
Особое значение в анализе рядов динамики придается расчету средних
темпов (коэффициентов) роста. Если можно пренебречь колеблемостью, то
средний теми роста определяют как геометрическую среднюю из цепных темпов
роста за п лет или из общего (базисного) темпа роста за п лет.
Средний темп роста представляет собой свободную обобщающую
характеристику интенсивности изменения уровней ряда динамики и показывает,
во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
В качестве основы и критерия правильности исчисления среднего темпа
роста (снижения) применяется обобщающий показатель, который определяется
21

как произведение цепных темпов роста, равное темпу роста за весь
рассматриваемый период. Если значение признака образуется как произведение
отдельных вариантов, то согласно общему правилу необходимо применять
среднюю геометрическую.
Так как средний темп роста представляет собой средний коэффициент роста,
выраженный в процентах (
100КT
), то для равностоящих рядов динамики
расчеты по средней геометрической сводятся к исчислению средних
коэффициентов роста из цепных по «цепному способу»:
,...
21
п
ц
р
п
ц
р
п
ц
рп
ц
р
ц
р
ц
р
КПККККК
(1.16)
где
n
– число цепных коэффициентов роста;
ц
рп
ц
р
КК ,...,
1
цепные коэффициенты роста;
б
р
К
базисный коэффициент роста за весь период.
Расчет среднего коэффициента роста может быть упрощен, если будут
известны уровни динамического ряда. Так как произведение цепных
коэффициентов роста равно базисному, то в подкоренное выражение
подставляется базисный коэффициент роста.
Формула для расчета среднего коэффициента роста для равностоящих рядов
динамики по «базисному способу» имеет вид:
,
1
0
m
n
б
р
y
y
К
(1.17)
где
п
у
уровень последнего периода;
0
у
уровень базисного периода;
m
– число уровней ряда динамики в изучаемом периоде, включая
базисный.
Средний темп прироста
пр
Т
вычисляется на основе среднего темпа роста
р
Т
, вычитанием из последнего 100%.
%100
рпр
ТТ
. (1.18)
Если уровни ряда динамики снижаются, то средний темп роста будет меньше
100%, а средний темп прироста – отрицательной величиной. Отрицательный темп
прироста – это средний темп сокращений. Он характеризует среднюю
относительную скорость снижения уровня.
Рассмотрим расчет средних темпов роста и средних темпов прироста по
формулам (1.16), (1.17) и (1.18) для уровней объема работ, выполненных по
договорам строительного подряда, и общей площади квартир, введенных в
действие жилищно-строительными кооперативами Тюменской области в период с
1995-2004 гг.
22

Средний годовой темп роста объема строительных работ за 1995-2004 гг.
составляет:
9
02,121467
32,110766
б
р
К
=0,9898. Средний годовой темп прироста равен
%100%98,98
пр
Т
=-1,02 %. Таким образом, в среднем ежегодно объем работ,
выполненных по договорам строительного подряда, за последнее десятилетие
уменьшался на 1,02% - это и есть средний годовой темп сокращений (или средняя
относительная скорость снижения уровня).
Средний годовой темп роста общей площади квартир, введенных в действие
жилищно-строительными кооперативами Тюменской области за 1995-2004 гг.
составляет:
9
42862
68772
б
р
К
=1,054. Средний годовой темп прироста равен
%100%4,105
пр
Т
=5,4%. Таким образом, в среднем ежегодно общая площадь
введенных в эксплуатацию квартир за последнее десятилетие увеличивалась на
5,4%.
2. ЭКОНОМИКО-СТАТИСТИЧЕСКИЙ АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
РАЗВИТИЯ СТРОИТЕЛЬСТВА ТЮМЕНСКОЙ ОБЛАСТИ
2.1 Выявление и характеристика основной тенденции развития строительства
Тюменской области
Важным направлением в исследовании закономерностей динамики
социально-экономических процессов является изучение общей тенденции
развития (тренда). Это можно осуществить, применяя специальные методы
анализа рядов динамики. Конкретное их использование зависит от характера
исходной информации и предопределяется задачами анализа.
Изменения уровней рядов динамики обусловливаются влиянием на
изучаемое явление ряда факторов, которые, как правило, неоднородны по силе,
направлению и времени их действия. Постоянно действующие факторы
23
оказывают на изучаемые явления определяющее влияние и формируют в рядах
динамики основную тенденцию развития (тренд). Воздействие других факторов
проявляется периодически. Это вызывает повторяемые во времени колебания
уровней рядов динамики, действие разовых факторов отображается случайными
(кратковременными) изменениями уровней рядов динамики.
Различные результаты действия постоянных, периодических и разовых
причин и факторов на уровни развития социально-экономических явлений во
времени обусловливают необходимость изучения основных компонентов рядов
динамики: тренда, периодических колебаний, случайных отклонений.
Особенностью изучения развития социально-экономических процессов во
времени является то, что в одних рядах динамики основная тенденция роста
проявляется при визуальном обзоре исходной информации, в других рядах
динамики общая тенденция развития непосредственно не проявляется. Она может
быть выражена расчетным путем в виде некоторого теоретического уровня.
Рассмотрим закономерность систематического спада, а затем подъема общей
площади квартир, введенных в действие жилищно-строительными кооперативами
Тюменской области в период с 1990-2004 гг. (табл. 2.1).
Таблица 2.1
Год 1 1990 1991 1992 1993 1994 1995 1996
Общая площадь
квартир
2
13888 22624 19932 32285 37937 42862 48944
продолжение табл. 2.1
1
1997 1998 1999 2000 2001 2002 2003 2004
2
30683 59124 50200 46720 44454 65043 64470 68772
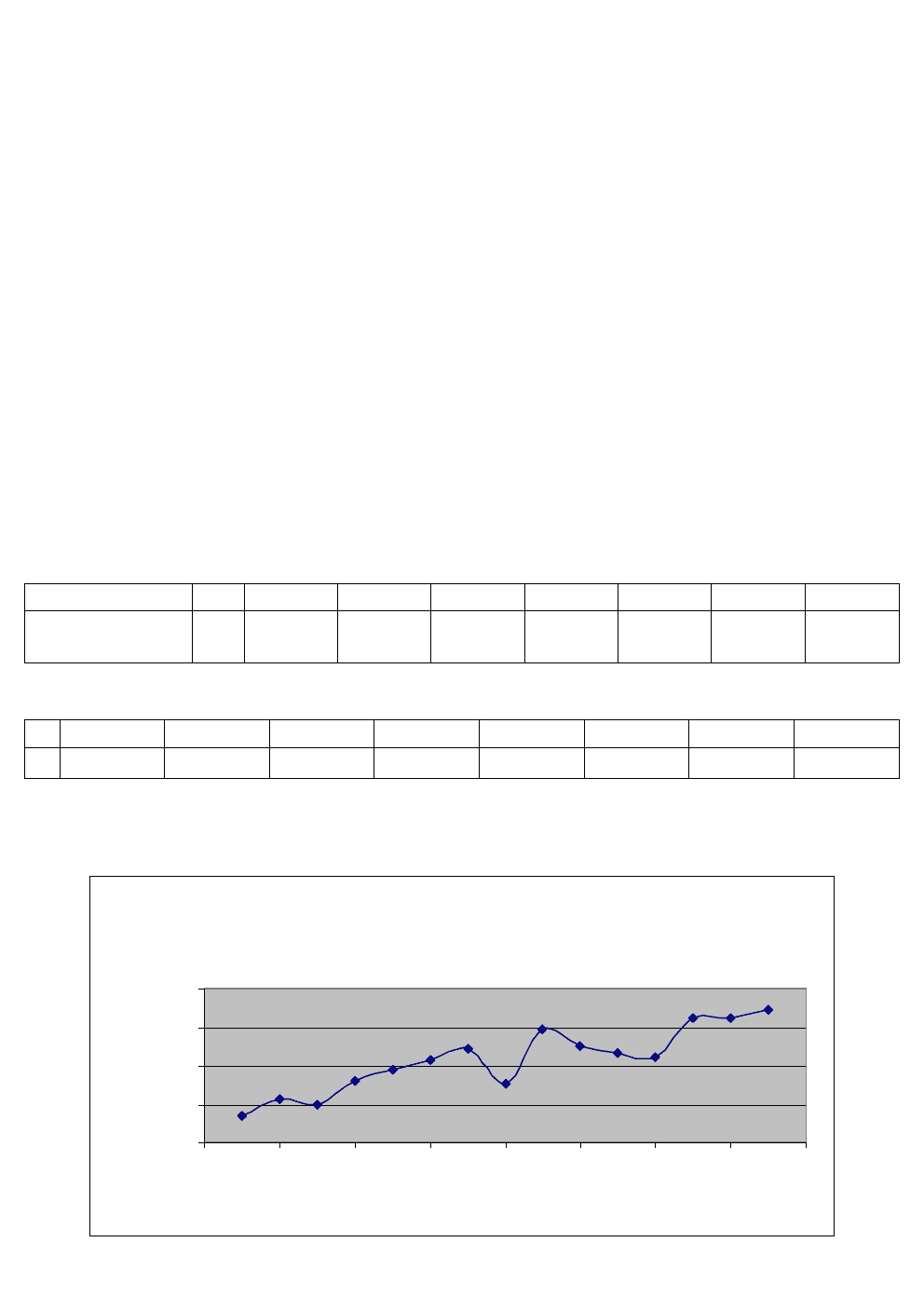
Большую наглядность основной тенденции развития общей площади
квартир можно получить из графического изображения ряда динамики (рис. 2.1).
Общая площадь квартир,введенных в действие
жилищно-строительными кооперативами
0
20000
40000
60000
80000
0 2 4 6 8 10 12 14 16
год
м2
Рис. 2.1. Объем Тюменской области с 1990-2004 гг.
24
Сравнивая уровни разных лет, можно заметить, что в 1997 и в 200-2001гг.
происходил спад общей площади квартир до 30683 и 44454 м
2
соответственно.
При визуальном обзоре можно предположить, что основная тенденция этого ряда
- линейная.
Для точного определения типа тренда существует несколько методов
обработки рядов динамики, а именно: метод укрупнения интервалов, метод
скользящей средней и аналитическое выравнивание. Во всех методах вместо
фактических уровней при обработке ряда рассчитываются иные (расчетные)
уровни, в которых тем или иным способом взаимопогашается действие
случайных факторов и тем самым уменьшается колеблемость уровней. Последние
в результате становятся как бы «выровненными», «сглаженными» по отношению
к исходным фактическим данным. Такие методы обработки рядов называются
сглаживанием или выравниванием рядов динамики.
Первым приемом выявления типа тенденции, не считая графического
изображения, служит метод укрупнения интервалов времени, для которых
определяется итоговое значение или средняя величина исследуемого показателя.
Этот метод особенно эффективен, если первоначальные уровни ряда относятся к
коротким промежуткам времени. В ряду с укрупненными интервалами времени
закономерность изменения уровней будет более наглядной.
Например, укрупним интервалы данного ряда до пяти лет и рассчитаем
суммарный и среднегодовой выпуск продукции по пятилеткам. Новые данные
будут выглядеть следующим образом (табл. 2.2):
Таблица 2.2
Пятилетка Общая площадь квартир, млрд. руб.
общий среднегодовой
1990-1994 126666 25333,2
1995-1999 231813 46362,6
2000-2004 289459 57891,8
Очевидно, что новые данные более четко выражают закономерность
изменения общей площади квартир, введенных в действие жилищно-
строительными кооперативами Тюменской области в период с 1990-2004 гг. в,
т.е. ее постепенный рост из года в год.
Метод скользящей средней величины состоит в вычислении средних уровней
динамического ряда последовательно, со сдвигом на один уровень. В табл. 2.3
приведена трехлетняя скользящая средняя: первая за 1990-1992 гг., вторая за
1991-1993 гг. и т. д. Каждая трехлетняя средняя относится ко второму (среднему)
году трехлетия, поэтому для первого и последнего года скользящая средняя
отсутствует. В общем виде при осреднении за m лет число скользящих средних
составит n - m + 1.
Таблица 2.3
Расчет скользящей средней по трем членам
Год Общая площадь квартир, Скользящая сумма Скользящая средняя
25

введенных в действие ЖСК
ТО, м
2
трех членов из трех членов
1990 13888 - -
1991 22624 56444 18815
1992
19932
74841 24947
1993
32285
90154 30051
1994 37937 113084 37695
1995 42862 129743 43248
1996
48944
122489 40830
1997
30683
138751 46250
1998
59124
140007 46669
1999
50200
156044 52015
2000
46720
141374 47125
2001
44454
156217 52072
2002 65043 173967 57989
2003 64470 198285 66095
2004
68772
- -
Сглаженный ряд более наглядно показывает тенденцию к росту уровней из
года в год. Эффект сглаживания, устраняющего колебания уровней за счет
случайных причин, хорошо виден также при графическом изображении
фактических и сглаженных уровней (рис. 2.2).
Общая площадь квартир,введенных в
действие жилищно-строительными
кооперативами
0
20000
40000
60000
80000
0 5 10 15 20
год
м2
эмпирический
уровень
сглаженный
уровень
Рис. 2.2. Динамика общей площади квартир, введенных в действие жилищно-
строительными кооперативами
Рассмотрим также закономерность систематического спада, а затем подъема
строительных работ на данных об объеме работ, выполненных по договорам
строительного подряда, Тюменской области в период с 1990-2004 гг. (табл. 2.4).
Таблица 2.4
Год 1 1990 1991 1992 1993 1994 1995 1996
Объем работ 2
170425 126455 102682 108432 103552 121467 101182
26

продолжение табл. 2.4
1
1997 1998 1999 2000 2001 2002 2003 2004
2
87623,6 71939 63090,51 72427,9 101036,9 107099,1 96067,92 110766,3
Большую наглядность основной тенденции развития объема работ,
выполненных по договорам строительного подряда, можно получить из
графического изображения ряда динамики (рис. 2.3).
Объем работ, выполненных по
договорам строительного подряда
0,00
20000,00
40000,00
60000,00
80000,00
100000,00
120000,00
140000,00
160000,00
180000,00
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
год
млрд. руб.
Рис. 2.3. Объем работ, выполненных по договорам строительного подряда
Тюменской области с 1990-2004 гг.
Сравнивая уровни разных лет, можно заметить, что с 1990 по 1999 гг.
происходил спад объема строительных работ, причем в 1999 году наблюдалось
самое большое его значение, а именно 63090,51 млрд. руб., и с 2000 по 2004 гг. - в
Тюменской области наблюдается подъем объема работ, выполненных по
договорам строительного подряда до отметки 110766,32 млрд. руб. При
визуальном обзоре можно предположить, что основная тенденция этого ряда
имеет форму параболы второго порядка.
Укрупним интервалы данного ряда. Новые данные выглядят следующим
образом (табл. 2.5):
Таблица 2.5
Пятилетка Объем строительных работ, млрд. руб.
общий среднегодовой
1990-1994 611546,25 122309,25
1995-1999 445302,18 89060,436
2000-2004 487398,20 97479,64
Очевидно, что новые данные более четко выражают закономерность
изменения объема строительных работ в период с 1990-2004 гг., т.е. его спад в
1995-1999 гг. Применим также метод скользящей средней (табл. 2.6).
27
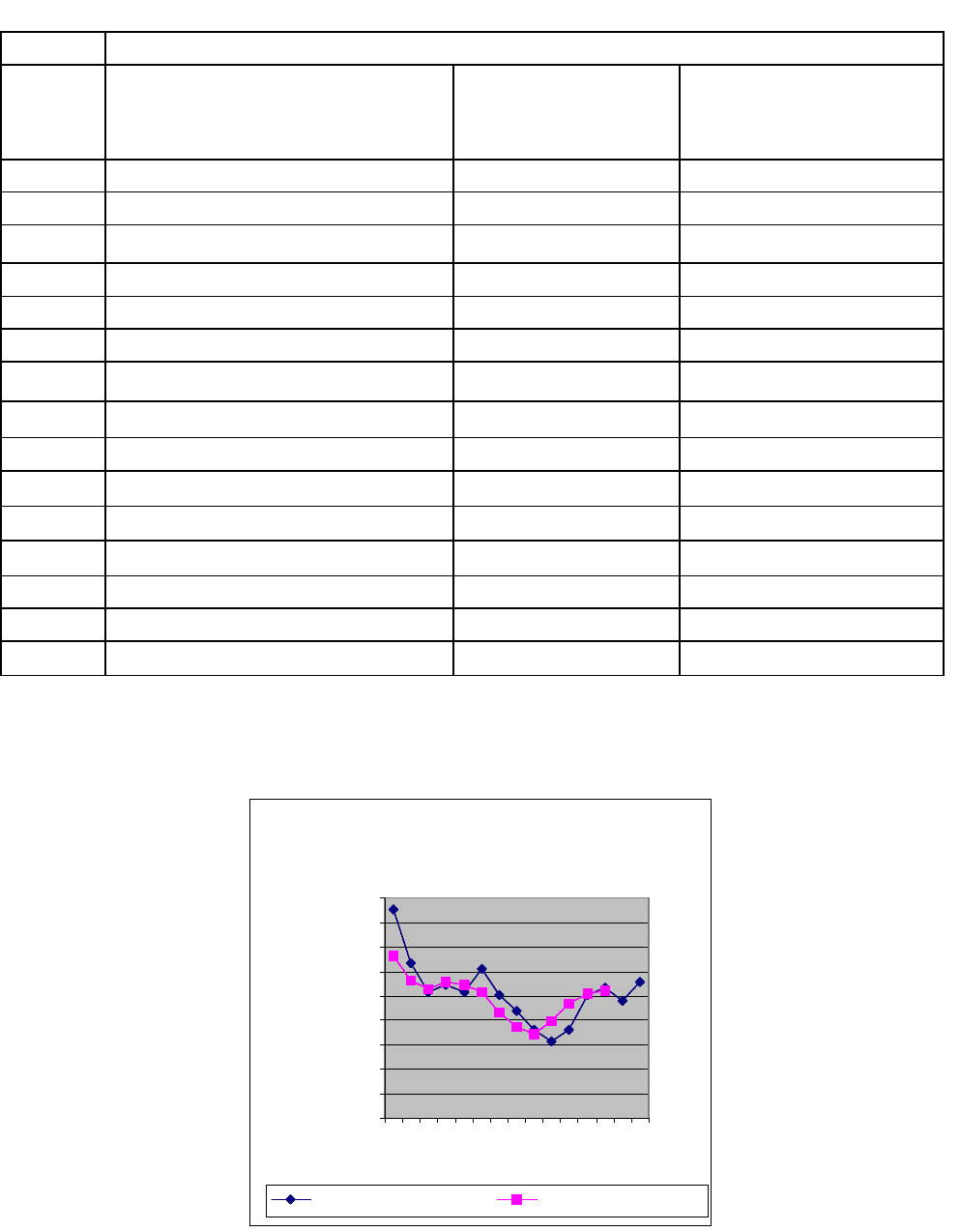
Таблица 2.6
Расчет скользящей средней по трем членам
Год Объем работ, выполненных
по договорам строительного
подряда, млрд. руб.
Скользящая сумма
трех членов
Скользящая средняя
из трех членов
1990 170424,93 - -
1991 126455,30 399561,93 133187,31
1992
102681,70
337568,88 112522,96
1993
108431,88
314666,02 104888,67
1994 103552,44 333451,34 111150,45
1995 121467,02 326201,48 108733,83
1996
101182,02
310272,67 103424,22
1997
87623,63
260744,66 86914,89
1998
71939,00
222653,14 74217,71
1999
63090,51
207457,41 69152,47
2000
72427,90
236555,33 78851,78
2001
101036,92
280563,96 93521,32
2002 107099,14 304203,98 101401,33
2003 96067,92 313933,38 104644,46
2004
110766,32
- -
Сглаженный ряд более наглядно показывает тенденцию к спаду, а затем
увеличению уровней из года в год (см. рис. 2.4).
Объем работ, выполненных по договорам
строительного подряда
0,00
20000,00
40000,00
60000,00
80000,00
100000,00
120000,00
140000,00
160000,00
180000,00
1
3
5
7
9
11
13
15
год
млрд. руб.
Эмпирический уровень Сглаженный уровень
Рис.2.4. Динамика объема работ, выполненных по договорам строительного
подряда, Тюменской области за 1990-2004гг.
28

Недостатком метода скользящей средней является то, что сглаженный ряд
«укорачивается» по сравнению с фактическим с двух концов: при нечетном m на
(m - 1)/2 с каждого конца, а при четном — на т/2 с каждого конца. Применяя этот
метод, надо помнить, что он сглаживает (устраняет) лишь случайные колебания.
Если же, например, ряд содержит сезонную волну, она сохранится и после
сглаживания методом скользящей средней.
Кроме этого, этот метод сглаживания, как и укрупнение интервалов, является
механическим, эмпирическим и не позволяет вы разить общую тенденцию
изменения уровней в виде математически модели.
Более совершенный метод обработки рядов динамики в целях устранения
случайных колебаний и выявлении тренда - выравнивание уровней ряда по
аналитическим формулам (или аналитическое выравнивание). Суть
аналитического выравнивания заключается в замене эмпирических
(фактических) уровней y
i
теоретическими y
t
, которые рассчитаны по
определенному уравнению, принятому за математическую модель тренда, где
теоретические уровни рассматриваются как функция времени: y
t
= f (t).
При этом каждый фактический уровень у, рассматривается как сумма двух
составляющих: y
t
= f(t)+
t
, где f(t)=y
t
- систематическая составляющая,
отражающая тренд и выраженная определенным уравнением, а
t
- случайная
величина, вызывающая колебания уровней вокруг тренда.
Определение теоретических (расчетных) уровней y
t
производится на основе
так называемой адекватной математической функции, которая наилучшим
образом отображает основную тенденцию ряда динамики.
Подбор адекватной функции осуществляется методом наименьших
квадратов минимальностью отклонений суммы квадратов между
теоретическими y
t
и эмпирическими y
i
уровнями (формула (2.1)):
min)(
2
å
it
yy
(2.1)
Значение уравнения (2.1) состоит в том, что при изучении тренда оно
принимается в качестве критерия оценки соответствия расчетных (теоретических)
уровней с фактическими (эмпирическими) уровнями ряда динамики.
Важнейшей проблемой, требующей своего решения при применении метода
аналитического выравнивания, является подбор математической функции, по
которой рассчитываются теоретические уровни тренда. От правильности решения
этой проблемы зависят выводы о закономерностях тренда изучаемых явлений.
Если выбранный тип математической функции адекватен основной тенденции
развития изучаемого явления во времени, то синтезированная на этой основе
трендовая модель может иметь полезное применение при изучении сезонных
колебаний, прогнозировании и других практических целях.
Одним из условий обоснованного применения метода аналитического
выравнивания в анализе рядов динамики является знание типов развития
социально-экономических явлений во времени, их основных отличительных
29

признаков. В практике статистического изучения тренда различают следующие
эталонные типы развития социально-экономических явлений во времени:
1) Равномерное развитие. Для этого типа динамики присущи постоянные
абсолютные приросты (формула(2.2)):
consty
ц
D
(2.2)
Основная тенденция развития в рядах динамики со стабильными
абсолютными приростами отображается уравнением прямолинейной функции
(формула(2.3)):
(2.3)
где а
0
и а
1
— параметры уравнения;
t — обозначение времени.
Параметр а
1
является коэффициентом регрессии, определяющим направление
развития.
2) Равноускоренное (равнозамедленное) развитие. Этому типу динамики
свойственно постоянное во времени увеличение (замедление) развития, т. е.
ускорения цепного абсолютного изменения более или менее постоянны. Уровни
таких рядов динамики изменяются с постоянными темпами прироста (формула
(2.4)):
constT
Пц
(2.4)
Основная тенденция развития в рядах динамики со стабильными темпами
прироста отображается функцией параболы второго порядка (формула(2.5)):
y
t
=a
o
+a
1
t+a
2
t
2
. (2.5)
В формуле (2.5) значения параметров а
0
и а
1
идентичны параметрам,
используемым в формуле (2.3). Параметр а
2
характеризует постоянное изменение
интенсивности развития (в единицу времени). При а
2
>0 происходит ускорение
развития, а при а
2
<0 идет процесс замедления роста;
3) Развитие с переменным ускорением (замедлением). Для этого типа
динамики основная тенденция развития выражается функцией параболы третьего
порядка (формула (2.6)):
y
t
=a
0
+a
1
t+a
2
t
2
+a
3
t
3
. (2.6)
В уравнении (2.6) параметр а
3
отображает изменение ускорения. При а
3
>0
ускорение возрастает, а при а
3
<0 ускорение замедляется;
4) Развитие по экспоненте. Этот тип динамики характеризуют стабильные
темпы роста (формула (2.7)):
30
,
10
taay
t
