Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

Flexible Robot Arms 24

-25

The generalized force corresponding to joint variable q

is the joint torque F

in those cases where the

boundary conditions are clamped, as will be assumed here.

(∂ K/∂

) −∂ K/∂q

∂V

∂q

∂V

∂q

= F

(24.89)

(∂ K/∂

) −∂ K/∂δ

∂V

∂δ

∂V

∂δ

= 0 (24.90)

24.2.6.1 Finite Element Representations

Additional detail can be added to a model by using more exact geometry for the structural elements;

however, a detailed ﬁnite element model will contain at least an order of magnitude more variables than

a well-derived assumed modes model. Fortunately, it is possible to combine the best of both techniques.

Examination of the above shows that the result of the speciﬁcation of the geometry (mass and stiffness

distribution) and all the analysis that ensues are embodied in a modal mass matrix, a modal stiffness matrix,

and similar parameter terms that account for the Coriolis and centrifugal terms. These matrices can also be

constructed from basis shapes resulting from a ﬁnite element representation of the components followed

by a speciﬁcation of approximate boundary conditions on each element separately and determination of

the resulting mode shape. This process is fairly direct for the ﬁnite element expert but beyond the scope

of this volume.

24.2.6.2 Approximations of This Method

The reader should be aware that the above technique, while satisfactory for most robotic applications, is

an approximation that will be inaccurate in some instances. Some of these instances have already been

alluded to, such as the case of large elastic deformation. More subtle inaccuracies exist that bear names

associated with the conditions of their occurrence. If the base of the arm is rotating rapidly about the Z

axis, vibrations in the X − Y plane would not account for the position dependent body forces effectively

stiffening the beam and leading to the phenomena of centrifugal stiffening. Hence, these equations are not

recommended for modeling helicopter rotors or similar rapidly rotating structures.

24.2.7 Simulation Form of the Equations

Twoformsof the equations of motion arecommonlyfound useful. Forpurposes of simulation the following

structure may be used:



(q) M

(q)

(q) M





=−



0 K





+ N(q,

q) + G(q) = R(q,

q, Q)

(24.91)

where

=rigid coordinates or joint variables

=ﬂexible coordinates

=the “mass” matrix for rigid and ﬂexible coordinates corresponding to the rigid (i, j = r )or

ﬂexible (i, j = f ) coordinates and equations

N(q,

q) =nonlinear Coriolis and centrifugal terms

G(q) =gravity effects

Q =externally applied forces

R =effect of external and restoring forces and all other nonconservative forces including friction

For serial arms it is generally more difﬁcult to produce this form of the equations, because all second

time derivatives must be collected. For simulation the second derivatives must be solved for, given the input

forces Q, the coordinates, and their ﬁrst derivatives. An integration scheme, often one capable of handling

stiff systems of equations, is then used to integrate these equations, forward in time twice, given initial

-26 Robotics and Automation Handbook

conditions and external forcing Q(t). The solution for

q requires either the inversion of its coefﬁcient

matrix or, more, efﬁciently another means such as singular decomposition to solve these equations for

known constant values (R is constant) of all other terms. This solution must be repeated at each time step,

leading to the major computational cost of the process.

24.2.8 Inverse Dynamics Form of the Equations

The inverse dynamics solution seeks the inputs Q that would yield a known time history of the coordinates

q, and

q. The inverse dynamics equations are less readily applied for ﬂexible arms than for rigid arms,

not due to the solution of the equation as given below, but because the values of q

are not readily obtained,

especially for some models. That situation is improved slightly if the rigid coordinates are chosen, not as

joint angles, but as the angles connecting the preceding and following axes. In such a way the tip of the arm

can be prescribed only in terms of q

. We know all velocities should come to zero after the arm reaches its

ﬁnal position. If gravity is to be considered, the static deﬂections at the initial and ﬁnal times will also be

needed. These can be solved for without knowing the dynamics. In the common case that Q = R

Q =



(q) M

(q)

(q) M







0 K





− N(q,

q) − G(q) (24.92)

In general Q is dependent on the vector T of motor torques or forces at the joints, and the distribution of

these effects is such that

Q =





T (24.93)

where T is the same dimension as q

. By rearranging the inverse dynamics equation we obtain



−M









+ N(q,

q) + G(q)

(24.94)

which is arranged with a vector of unknowns on the left side of the equation. Unknowns may also appear in

the vector of nonlinear and gravitational terms which contain q

and

, and strictly speaking, the solution

must proceed simultaneously. In practice these are typically weak functions of the ﬂexible variables and

the solution can proceed as a differential-algebraic equation.

It is worth noting what happens if we choose other rigid coordinates, such that the tip position is not

described by q

alone. Now B

is zero, B

= I , and the tip position is unknown. We may be satisﬁed

with specifying the joint coordinates, however, during the motion of the robot and accept the resulting

deﬂection of the tip. Further note that the equations are likely to be nonminimum phase. Resorting to

linear thinking for simplicity, the transfer functions have zeros in the right half plane. The inverse dynamics

effectively inverts the transfer function giving poles in the right half plane. Normal solution techniques

produce an unstable solution which is causal. Another solution, the acausal, stable solution exists and will

be found to be useful when we discuss control via inverse dynamics.

24.2.9 System Characteristic Behavior

Nonminimum phase behavior will be observed at the tip of a uniform beam subject to a torque input at its

root. In a ﬂexible arm this manifests itself as an initial reverse action to a step torque input. In other words,

the initial movement of the tip is in the opposite direction of its ﬁnal displacement. The consequences

of this behavior are pervasive if the tip position is measured and used for feedback control. To see this

effect, a linear analysis is sufﬁcient, and the transfer matrix frequency domain analysis is well suited for this

purpose. The nonminimum phase in this case is described by zeros in the right half plane for the transfer

function from torque to position. When a feedback loop is closed, the root locus analysis shows that the

Flexible Robot Arms 24

-27

positive zero must attract one branch of the root locus into the right, unstable region of the complex plane.

The usual light damping of the ﬂexible vibration modes allows this to happen with low values of feedback

gain. A uniform beam shows these characteristics, and it has been shown (Girvin [14]) that tapering a

beam reduces the severity of the nonminimum phase problem but does not eliminate it.

24.2.10 Reduction of Computational Complexity

The equations presented above can result in very complex relationships that need to be solved in order to

be used either for simulation or for inverse dynamics. It is worth enumerating several ways of reducing

this complexity. The number of basis shapes can be reduced if assumed modes close to the true modes

are used for basis shapes. Several terms in the equation involve integration of the product of two basis

shapes. If orthogonal assumed modes are used the cross product of two different mode shapes is zero when

integrated over the length of the beam.

24.3 Control

The ﬂexibility of a motion system becomes an issue when the controlled natural frequency becomes

comparable to the vibrational frequencies of the arm in the direction of movement. One of the ﬁrst things

to know is when this might occur. If it is expected to be an issue, the next thing to consider is ways to

ameliorate the problem. This involves a great number of possibilities, many of which involve control, but

not exclusively control. Control should not be interpreted to exclusively mean feedback control, because

open loop approaches are also very valuable.

24.3.1 Independent Proportional Plus Derivative Joint Control

The vast majority of feedback controlled motion devices, including mechanical arms, use some of pro-

portional plus integral plus derivative (PID) control. Velocity feedback may be an alternative to derivative

feedback. The simplest approach here is to apply the PID algorithm to each joint independently. In this

case the actuation of other joints can create a disturbance on each joint which could have been anticipated

with a centralized approach. This problem was analyzed in the earliest work considering the ﬂexibility of

robot arms [11]. Because the parameters involved in a PD controller (no integral action because it has

minimal effect) are only two per joint, the problem can be effectively studied by simply sweeping through

the design space. The pole positions of the controlled ﬂexible system provide a way to judge the controller

effectiveness. PD control of a rigid degree-of-freedom enables arbitrary placement of the system poles.

The dominant poles of the ﬂexible arm behave as a rigid system when the lowest natural frequency of

the system is about one-ﬁfth the ﬂexible natural frequency with the joints clamped. Critical damping on

the dominant modes cannot be obtained by adding additional derivative gain when the servo frequency

is above about one third of the structural natural frequency. Damping reaches a maximum and then de-

creases with additional velocity or derivative feedback. The effect of derivative feedback for three values

of proportional feedback is sketched in Figure 24.4. While more joints and links distort this conclusion to

some extent, servo bandwidths above one third the system’s natural frequency are very hard to achieve.

To the extent that true PD action can be obtained, the independent joint controlled arm will not go

unstable but will become highly oscillatory with high gains. The root locus converges to the position of

the clamped joint natural frequencies which make up the zeros of this system since this is the condition

of zero joint motion. Higher modes that start at the pinned-free natural frequencies are seen to converge

to the higher clamped-free natural frequencies. Zero joint motion means the joints are unable to move in

response to vibration and thereby unable to remove the vibrational energy. Note that heavily geared joints

or joints actuated by hydraulic actuators may not be back drivable in any event, and hence, the shaping

of the commanded motion becomes the most effective way to damp vibration. Low gains still have the

effect of smoothing out abrupt commands that would excite vibration although at the expense of rapid

and precise response.

-28 Robotics and Automation Handbook

−3.0 −1.0−2.0

1.0

2.0

3.0

4.0

5.0

6.0

ζ = 5.0

ζ = 0.0

ζ = 1.0

1 M (jω/ω

)

Higher Order Roots

/ω

= 0.167

/ω

= 0.383

/ω

= 0.500

Values of ζ appearing for each case are:

0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7,

0.8, 0.9, 1.0, 2.0, 3.0, 4.0, 5.0.

RE (jω/ω

)

0.167

0.383

ζ = 1.0

= 0.7

= 0.9

0.5

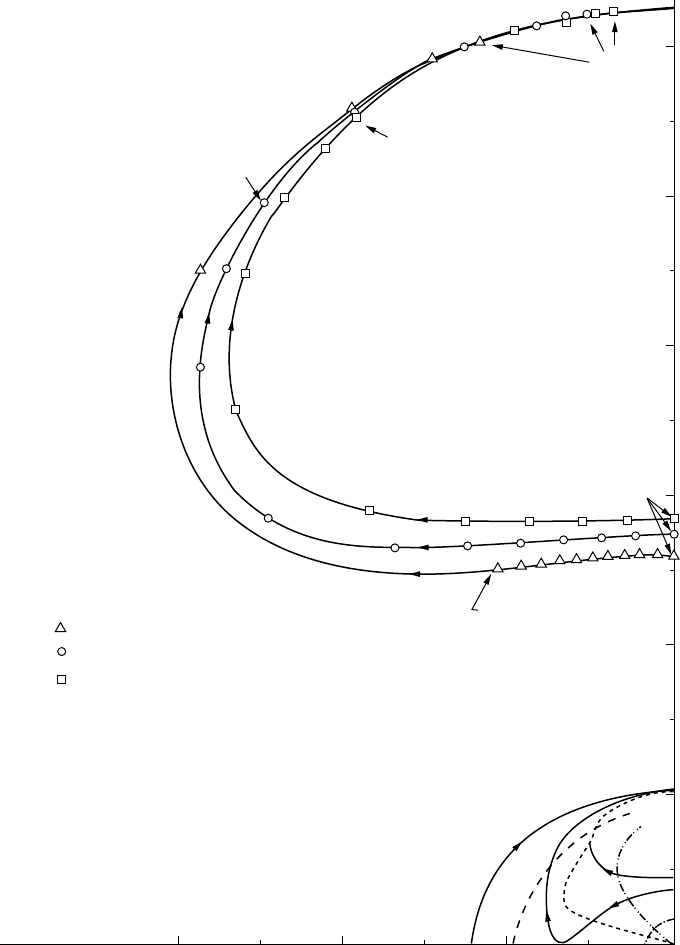
FIGURE 24.4 Root loci for three proportional gains as derivative gain varies.

When multiple axes are controlled with PD control, the details become more complicated but the overall

behavior remains the same. If two joints contribute to the same vibrational mode, they both offer points

at which energy can be put into or taken out of that mode. The limiting case is that energy can be taken

out in a distributed fashion, giving a bandwidth which is a larger percentage of the natural frequency but

not exceeding it.

Flexible Robot Arms 24

-29

–1 –0.8 –0.6 –0.4 –0.2 0

Real Axis

0.2 0.4 0.6 0.8 1

–2

–1.5

–1

–0.5

0.5

1.5

Image Axis

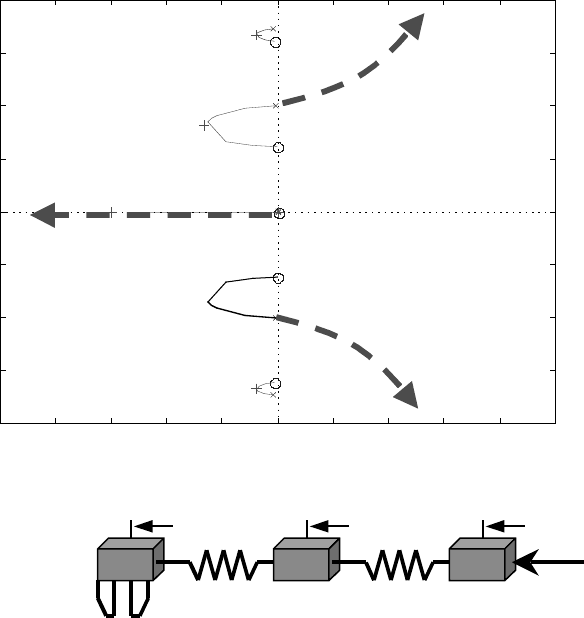
FIGURE 24.5 Noncollocated feedback of dx

/dt to apply force at x

produces unstable (dashed) root locus. (Collo-

cated feedback shown in solid lines.)

To avert the limitations of ﬂexibility a reasonable but na

ıve approach to improve control performance,

PID control based on measuring the end effector position fails because of the nonminimum phase behavior

(resulting from noncollocated sensors and actuators) of the system. Even simple systems of this type

involving two masses connected by a spring illustrate the effect as shown in Figure 24.5 in a root locus

plot.

24.3.2 Advanced Feedback Control Schemes

Because the number of control algorithms that have been applied to ﬂexible arms is extremely large, it is

not possible to cover all of them in this treatment. Other texts and handbooks exist to present the details

of these algorithms [15]. It is also impossible to verify that all of these approaches have practical merit,

although there may be merit in speciﬁc cases to all of them. In this subsection the discussion will begin

with the objectives and obstacles to practical advantages of these designs.

24.3.2.1 Obstacles and Objectives for Advanced Schemes

The modeling of the ﬂexible arm involves many assumptions and presumptions. We assume that joint

friction is linear or at least known. We presume to know the mass, stiffness properties, and geometries of

the links and payloads. We have assumed a serial structure or at least one that could be approximated as

such. Some of the controls proposed use measurements of the system states or related variables. Sensors

-30 Robotics and Automation Handbook

to measure these variables over the workspace may not exist, and actuators that apply desired (collocated)

inputs are unavailable or inappropriate. Some traditional actuators are not back drivable and hence don’t

serve as force or torque sources as the algorithms require. Computation to implement some algorithms is

enormous, and hardware to perform these computations (typically done digitally) does not always exist

at this time although the trend in computational speed is encouraging. Related to the computational

complexity is the model order. Because a perfect model of the structure would contain an inﬁnite number

of modes, practical control design often violates perfection by working with a limited number of modes.

Hence, the unmodeled modes may be excited by our attempts to control the modeled modes (control

spillover), or our attempt to measure the modeled modes may be corrupted by the unmodeled modes

(measurement spillover) that do affect the measurement. One of the objectives of a practical controller is

to overcome these obstacles and thereby move the ﬂexible arm more rapidly, precisely, and reliably through

its prescribed motions.

24.3.2.2 State Feedback with Observers

The ﬂexibility is modeled as a collection of second order equations that interact. In addition, the actuators

will add dynamics that may be important. By converting this model to a state space model the control task

is reduced to moving the arm states to a desired point in state space. That desired point is based on the

desired position and velocity of the end effector, thus specifying the output of the system, plus the fact that

all vibrations should quickly converge to zero. Very powerful techniques exist for doing this if the model

of the system is linear. While the model is never perfectly linear, linearity may be a good approximation in

the region around an operating point of larger or smaller size.

To implement a regulator bringing the state to the origin of the state space the following model and

feedback law can be used. The output is the vector y. The plant matrix A, the input matrix B, the output

matrix C, and the feed through matrix D are all required to be of appropriate dimension.

x = Ax + Bu

u = Kx

(24.95)

y = Cx + Du

Anextensionof these basic equations can producea controllerthat tracksa time varying referencetrajectory

as well. The linear equations can be written so that the origin of the state space produces the desired value

of y. There is no unique choice for states x. This allows one to transform to different representations for

different purposes. In terms of the models derived above the state, variables may be joint variables and

their derivatives and deﬂection variables and their derivatives.

The ﬁrst obstacle to this algorithm is measurement of all the needed states. In particular the deﬂection

variables and their derivatives are not directly available. Strain gages have been used to effectively obtain

this information and state feedback is then approximately achievable [16, 17, 18]. For each basis shape

used to model a beam, one additional measurement will enable calculation of its amplitude. The derivative

of that amplitude can then be approximated with a ﬁltered difference equation.

Stateobserversaredynamic systemsthat use presentand past measurementsof some outputs toconverge

on estimates of the complete system states. Full order observers have the same number of states as the

system they observe, while reduced order observers allow the measured variables to be used directly with a

proportional reduction of the observer order. Observers, that have been optimized according to a quadratic

performance index assuming Gaussian noise is corrupting the measurements and the control input, are

often referred to as Kalman ﬁlters after the pioneer in the use of this technique.

Evaluation of the feedback matrix K and the gains of the observer system can be done in various ways.

The optimization scheme referred to above is popular but requires some knowledge or assumption of the

strengths of the noises corrupting inputs and measurements. Pole placement is another approach that

allows the engineer more direct inﬂuence over the resulting dynamics. The choice of pole positions that

are “natural” for the system and yet desirable for the application can be challenging. These approaches are

discussed in appropriate references [15].

Flexible Robot Arms 24

-31

Knowledge of the plant model is required to construct the observer and to design the feedback matrix.

Sensitivity to error in this model is one of the major issues when seeking high performance from state

feedback. Nonlinear models complicate this issue immensely.

24.3.2.3 Strain and Strain Rate Feedback

Joint position is commonly differentiated numerically to approximate velocity and similarly link deﬂection

can be differentiated numerically to complete the vector of state variables to be used in the state feedback

equation. Thus, to control two modes, at least two strain gage readings are needed for effective ﬂexible arm

control which is not extremely sensitive to model parameters [16]. This approach has been implemented

with good results as shown in Yuan [19]. Those experiments incorporated hydraulic actuation ofa6m

long, two-link arm and roughly cut the settling time of PD control in half. Hence, the complexity of an

observer was not required, although ﬁltering of the noisy differentiated signals may be appropriate.

One of the obstacles to the general application of strain feedback, or state feedback in general, is the

lack of a credible trajectory for the ﬂexible state variables. The end user knows where the tip should be,

but the associated strain will not be zero during the move. See the section below on inverse dynamics for

a solution to this dilemma.

24.3.2.4 Passive Controller Design with Tip Position Feedback

While it is natural to want to feed back the position of the point of interest, the nonminimum phase nature

of the ﬂexible link arm results in instability. Nonminimum phase in linear cases results from zeros of the

transfer function in the right half plane. The output can be modiﬁed to be passive and of minimum phase

by closing an inner loop or by redeﬁning the output as a modiﬁed function of the measured states. For

example, if tip position is computed from a measured joint angle θ and a measured deﬂection variable δ for

a link of length l, the form of the equation will be (tip position) = lθ +δ and the system is nonminimum

phase. If, on the other hand, the (reﬂected tip position) = lθ − δ is used for feedback control, the system

is passive and can be readily controlled for moderate ﬂexibility [20]. Obergfell [21] measured deﬂection

of each link of a two link ﬂexible arm and closed each inner loop using this measurement. Then a vision

measurement of the tip position was used to control the passiﬁed system with a simple controller. He used

classical root locus techniques to complete compensator design. The device and the nature of the results

are shown in Figure 24.6 and Figure 24.7.

24.3.2.5 Sliding Mode Control

Slidingmode controloperatesintwophases. First, thesystemis driven instatespacetowarda sliding surface.

On reaching the sliding surface, the control is switched in a manner to move along the surface toward the

origin, set up to be the desired equilibrium point. The switching operation permits an extremely robust

behavior for many systems, but if there are unmodeled dynamics, the abrupt changes may excite these

modes more strongly than other controllers. Given the concern for robustness with model imperfections

and changes, the sliding mode has a natural appeal. The implementation of sliding mode control is subject

to some of the same problems as state feedback controllers; that is, knowledge of the state is difﬁcult to

obtain by measurement. Frame [22] has used observers based on a combination of joint position, tip

acceleration, and tip position (via camera) measurements. The results are recent and, while promising,

have not produced a clear advantage over state feedback.

24.3.3 Open Loop and Feedforward Control

Three matters for discussion in this section are the initial generation of the motion trajectory for a ﬂexible

link system, either the end point or the joints and the modiﬁcation of an existing trajectory to create a more

compatible input. Finally, by observing the errors in tracking a desired trajectory, the learning control

approach can improve the trajectory on successive iterations, reducing the demands on the feedback

control.

-32 Robotics and Automation Handbook

FIGURE 24.6 The experimental arm RALF (Robotic Arm Large and Flexible). (Total length about 6 m, lowest natural

frequency about 3 Hz.)

24.3.3.1 Trajectory Specification

Among the most popular trajectory forms is the trapezoidal velocity proﬁle that results from the desire

to move in minimum time from point to point, with constraints on acceleration and velocity. This bang-

bang solution creates extreme values of jerk (the third derivative of position) and consequently excites the

ﬂexible modes of an arm. A modiﬁed approach consists of also limiting the value of jerk and minimizing

move time under this new constraint.

24.3.3.2 Filtering of Commands for Improved Trajectories

Small changes in the speed along a given path of motion can have major changes in the resulting vibration

of a ﬂexible arm. This is because the excitation is largely the result of jerk, the second derivative of

speed, and is not readily apparent to someone planning a velocity proﬁle, much less a position proﬁle.

Flexible Robot Arms 24

-33

–1.84 –1.82

–1.8

Tip x-position (m)

Tip y-position (m)

–1.78 –1.76

5.14

5.16

5.18

5.2

5.22

5.24

(a)

–1.84 –1.82 –1.8 –1.78 –1.76

5.14

5.16

5.18

5.2

5.22

5.24

Tip x-position (m)

Tip y-position (m)

(b)

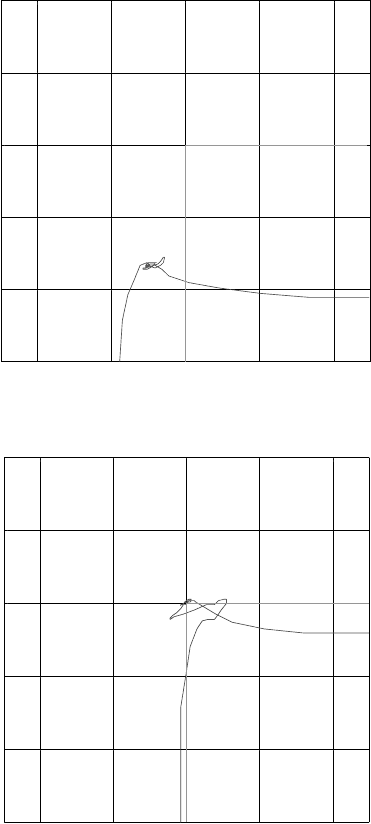
FIGURE 24.7 (a) Path followed without tip position feedback. (Commanded trajectory is a square, partially shown

in green and actual trajectory in red.) (b) Path followed with tip position feedback. (Commanded trajectory is a square,

partially shown in green and actual trajectory in red.)

Filtering the nominal input trajectory can make small adjustments to all trajectories entered and relieve

the end user from this task. Filters commonly used are the low pass ﬁlter, notch ﬁlter, and the time delay

ﬁlter.

Low pass ﬁltering can be performed by either digital or analog means. Typically a cutoff frequency and

a rate of roll off are determined. The rate of roll off is determined by the order of the ﬁlter n (number

of integrators required), and the cutoff frequency is determined by the selection of parameters. Standard

techniques for parameter selection are available [23], and ﬁlter poles are placed according to standard

patterns. The analog Butterworth ﬁlter of order n, a popular low pass ﬁlter, is based on 2n poles evenly

-34 Robotics and Automation Handbook

spaced around a circle, symmetric about the real axis, and no zeros. The stable poles are maintained in the

ﬁlter design. The ﬁlter can then be converted to a digital ﬁlter by various mapping techniques. Chebyshev

ﬁlters have poles similarly placed about an ellipse, and superior frequency domain speciﬁcations are

achieved in the pass band but with some ﬂuctuations in the magnitude of the response. For ﬁltering the

robot trajectory, we are also concerned about the time response of the ﬁlter itself and do not want the ﬁlter

to insert oscillations of its own. Implementation of a low pass ﬁlter such as a Butterworth ﬁlter results in an

inﬁnite impulse response (IIR) ﬁlter as a result of the system poles. Theoretically, the response to an input

never dies out. Artifacts of the ﬁlter include phase shift and an extension of the period of time over which

the commanded motion continues. In the design of the low pass ﬁlter the engineer must base the cutoff

frequency on the vibration frequencies of the arm. All components with frequencies above the cutoff are

reduced in magnitude.

Time delay ﬁltering is readily implemented with a digital controller but not with an analog controller.

Effectively, every ﬁnite impulse response (FIR) ﬁlter is a time delay ﬁlter. The input is received by the ﬁlter,

and the output based on that input is given for only a ﬁnite time period thereafter. When implemented

by a digital delay line with n delays of time T and a zero-order hold, a single input enduring for a period

T would produce n outputs that were each piecewise constant for each period of time T. While low pass

and other ﬁlters can be implemented in FIR form, our interest is with a speciﬁctypeofﬁlter that places

zeros at appropriate places to cancel arm vibrations. The placement of these zeros requires knowledge of

the arm’s vibrational frequency. When contrasted with the IIR ﬁlter, the FIR ﬁlter stretches the input by

only a known time, at most nT. The operation of this ﬁlter is explained by a combination of time response

and frequency response.

The early version of a command shaping ﬁlter [24, 25] suffered from excessive sensitivity to variations

in the plant. Since then a revised form was proposed [26], and a number of researchers have explored

variations on this theme [27, 28, 29, 30]. The problem of sensitivity has been addressed in several ways that

can be grouped into two approaches: increase robustness or adapt the ﬁlter [31]. Increasing robustness

allows the resonant frequencies to drift somewhat during operation while remaining in a broadened notch

of low response. The notch is broadened by placement of multiple zeros. Unfortunately this requires

additional delay in completing the ﬁltered command. The time-delay ﬁlter in various forms has become a

widely used approach to canceling vibration with minimal demand on controller complexity and design

sophistication. Its effectiveness can be understood in terms of the superposition that linear systems obey.

An impulse input is separated into several terms, which when combined by superposition cancel the

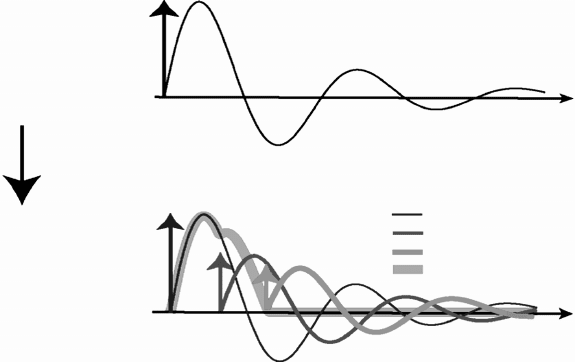
vibration as shown in Figure 24.8.

Single Impulse

Shaped with

a Three-Term

Command Shaper

1st Impulse Response

2nd Impulse Response

3rd Impulse Response

Resultant Response

Single Impulse

time

0 ∆ 2∆

FIGURE 24.8 Effect of three term OAT command shaping ﬁlter.