Kurfess T.R. Robotics and Automation Handbook

Подождите немного. Документ загружается.

Flexible Robot Arms 24

-5

high feedback control gains to control the joint. In terms of material damping, a wide range of damping

values is observed and composites tend to have more damping than metals.

24.2.1.1.3 Idealized Structures and Loading

Exact evaluation of the stress in a robot component may require ﬁnite element analysis. For present

purposes it will be more valuable to compose the robot from idealized structures tractable to analytical

determination of stress and deﬂection. In particular we will use bars in compression, shafts in torsion,

and beams in bending. For static deﬂection the load and the elastic properties are needed. For dynamic

deﬂectionthe mass propertiesarealsoneeded. Geometry willcontributetoboth mass and elasticproperties.

24.2.1.1.3.1 Bars and Compression

A bar element is considered for axial loading. Almost pure compression or tension will result for a strut

or similar element pinned at each end. In this case the static deﬂection δ is also axial and predicted simply

and accurately by the assumption of plane strain. If the cross-sectional area A is constant over the length

L,deﬂection δ under applied axial force F

δ =

= α

(24.2)

If A is not constant, the deﬂection is obtained by integrating a differential deﬂection (axial strain) over

the length with the area A(x) variable. Normal stress is approximately

σ = F

The dynamic behavior of a bar alone is rarely of concern with robots of conventional size if the bar

only experiences compression. This is because there are usually other components exhibiting more severe

deﬂection and because buckling constrains the ratio L/A to high values. The bar element can be used to

represent “tension only” components including cables and bands. In these cases buckling does not limit

L/A and the deﬂection can be substantial. Dynamic behavior incorporates mass as well. The mass of the

bar in tension is reduced as the cross-sectional area is reduced with the resulting effect that the natural

frequency is related to the speed of sound in the bar, which is invariant with the geometry and high relative

to other dynamic phenomena that impact robot performance. Thus, the bar plays the role of a spring for

most ﬂexible robot analysis; its mass can be considered lumped, if considered at all, and does not warrant

consideration as a distributed parameter effect.

24.2.1.1.3.2 Shafts and Torsion

Pure torsion is a fair representation of drive shaft loading. Arm structural elements also may experience

torsion in conjunction with bending or compression, and to a reasonable approximation the effects can be

added or superimposed. The simple case we will build on is a circular cross section, either solid or hollow.

The torque T acting on a circular tube of length l with cross-section polar moment of inertia J produces

a rotation of one end with respect to the other of θ,where

θ =

= α

θ T

T (24.3)

The pure shear τ resulting on the plane perpendicular to the axis of the torsion is approximately linear

with the radial distance r, giving the maximum at the outer radius R of

max

(24.4)

-6 Robotics and Automation Handbook

(

)

Neutral axis

FIGURE 24.1 Geometry of bending deformation.

When the cross section is not circular an approximate analysis is often used that is accurate as long as the

cross section is not prone to extreme warping with torsion. In this analysis

θ =

= α

θ T

T (24.5)

max

(24.6)

where K and Q are geometry dependent factors found in various handbooks and references such as

Norton [2].

24.2.1.1.3.3 Beams and Bending

The simple theory of beams is remarkably accurate for slender beams with cross sections that are not

extreme in their departure from a rectangle. If the beam has a deﬂection w such that at the position x,

the second derivative ∂

w/∂ x

is approximately equal to 1/r,wherer is the radius of curvature of the

neutral axis. As illustrated in Figure 24.1, the further assumption that planes perpendicular to the neutral

axis remain planes dictates the amount of elongation δ that takes place on the outer edge of the element

of length dx. With any ﬁnite curvature, an angle θ subtends the distance dx = r θ at a radius r from the

center of the local circular arc, that is, along the neutral axis. The strain along the neutral axis is zero by

deﬁnition. Moving to the outermost ﬁber of the beam, a distance c from the neutral axis, means the angle

θ subtends a greater distance of dx + δ = (c + r )θ. The combination of these relationships means the

strain at the outermost ﬁber is

ε = c

∂

∂x

= c

∂

∂x

(24.7)

By the simple beam theory the normal stress σ in the outermost ﬁber would be Eε or

σ = Ec

∂

∂x

dx (24.8)

and would vary linearly along y, the distance from the neutral axis. The moment M(x) developed at the

cross section by normal stress is found by integrating over the area of the cross section the stress times the

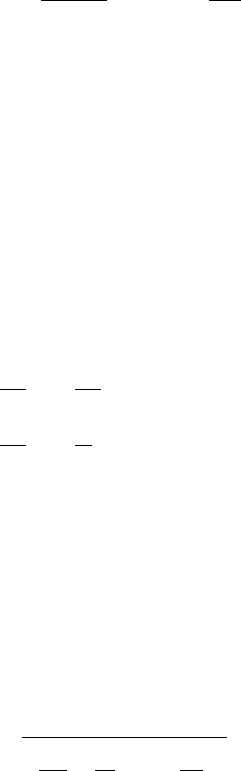
Flexible Robot Arms 24

-7

distance from the neutral axis times the differential area.

M(x) =



Area

σ (x, y)y

ydA = EI(x)

∂

∂x

(24.9)

where I (x) is the cross section’s area moment of inertia about the neutral axis at x.

I =



y max

y min

(24.10)

The deformation, displacement, and rotation, at the end of a loaded beam is readily computed from the

moment equation above when knowing the loading and deﬂection constraints on the beam. Loading could

occur in any location and as a concentrated or distributed force (perpendicular to the neutral axis) or

moment (about an axis perpendicular to the plane of bending). Tabulations of these loading effects are

found in more specialized handbooks [3] and it is productive here to cite only the response of a beam with

one end constrained not to translate or rotate with the other end completely free. Apply to the free end of

this beam a force F

and a moment M

, and the resulting deﬂection w(l) and rotation θ(l) at the end will

w(x)|

x=l

3EI

2EI

= α

+ α

(24.11)

(x)|

x=l

2EI

= α

θF

+ α

θM

The second form of these two equations identiﬁes coefﬁcients referred to later in this section and tells you

how to compute them for the case of uniform beams. Tapered, shaped, or stepped beams have coefﬁcients

that can be found from the deﬂection equation or in handbooks.

24.2.1.1.3.4 Combinations of Loading

In many situations it is acceptable to superimpose torsion, bending, and compression from the above

simple cases to calculate deformation and stress. The worst case stress will be where maximum axial

normal stress from bending is increased by the normal stress from axial forces. At this same point the shear

from torsion occurs and is maximum. The plane stress approximation is valid here and the von Mises

stress is found (assuming a circular cross section of outer radius R)tobe











Extreme cases require a more complex analysis beyond the scope of this section. The boundary between

acceptable and unacceptable is fuzzy and case dependent, but if any component of loading is modiﬁed by

a signiﬁcant fraction of the factor of safety, a more detailed analysis should be undertaken. For example,

if axial torsion T on a beam is realigned by 10

◦

, the bending moment on the beam is increased by about

0.18 T. An extremely slender beam could undergo 10

◦

of deformation without failure but the addition of

an additional bending moment of 0.18 T should be further considered. An exception to this proportional

effect is buckling behavior which is treated next.

24.2.1.1.4 Buckling

Bending becomes the most pronounced mode of stress and deﬂection in most beam type elements,

including arm links. The na

ıve designer is, therefore, tempted to place the maximum material at the

maximum distance from the neutral axis. Because bending may take place about any axis perpendicular to

the neutral axis, circular crosssections are attractive as they also resist torsion about the beam axis well. Why

not carry this to the extreme of very thin walls located at extreme distances from the neutral axis so that the

arm cross section is similar to an aluminum beverage can? The limitation may come from one or more of

-8 Robotics and Automation Handbook

several sources: arm bulk (limiting access), manufacturing difﬁculty, or the tendency of a thin wall cylinder

to buckle. Buckling is a structural instability in which the imperfections of construction and loading result

in a sudden drastic change in structure geometry. For the empty aluminum can, shell buckling alters the

geometry of the load bearing material, allowing localized stresses to rise and the geometry of the arm to be

destroyed. (Note that a pressurized drink can does not buckle so easily, so a thin, pressurized arm might

actually have merit.) Another form of buckling, column buckling, is typical of beams with small cross

sections. When such beams have a compressive axial load not perfectly aligned with a perfectly straight

neutral axis, the beam buckles in “column buckling” that was the subject of a classical analysis by Euler, an

analysis which still bears his name. Finally, “torsional buckling” arises from small cross sections subject to

imperfections in the straightness of the neutral axis or other loads which deﬂect the neutral axis a small

amount. The criticalloads predictedby the simple analyses beloware typicallytoo optimistic for arm design

and must be generously ampliﬁed in the case of robot arms, which are subjected to many unexpected and

complex loads. Nevertheless, it is important to realize there are constraints on arm geometry other than

ﬂexibility that interplay with our main focus of ﬂexible arms.

24.2.1.1.4.1 Column Buckling

Euler’s classical analysis of slender columns determines a bifurcation point at which an alternative shape of

the column is possible. The shape for simple uniform columns is a sinusoid, the periods of which depend

on the boundary conditions. More restrictive boundary conditions result in a shorter period and in turn

a higher critical load. The critical compressive load is

critical

eff

EAk

eff

critical

eff

(24.12)

where

k =radius of gyration corresponding to the cross section shape

eff

=the effective column length, dependent on end-constraint conditions

=l for pinned-pinned ends

=2l for ﬁxed (clamped)-free ends

=0.707l for ﬁxed-pinned ends

=0.5l for ﬁxed-ﬁxed ends

While arm structures will not be sized on buckling alone, this analysis shows a sensitivity to the cross

section shape and the link length.

24.2.1.1.4.2 Shell Buckling

The thin drink can is prone to shell buckling at locations of compressive stress. Here the classical analysis

yields a critical stress

critical

√

3(1 −ν

)





(24.13)

where

t = wall thickness

R =radius of cylindrical shell

ν =Poisson’s ratio for the material

E =Young’s modulus

Note that this is expressed in terms of a critical stress locally in the shell. Where that stress distributed over

a thin circular annulus with area 2πRt, the critical load becomes independent of R and dependent on t

. In

terms of stress, the ratio of thickness to radius is the key geometric feature that controls the susceptibility

to shell buckling for a more general geometry.

Flexible Robot Arms 24

-9

24.2.1.1.4.3 Torsional Buckling

Torsional buckling is a third possibility for unstable behavior. If a slender shaft is simply supported (free

to rotate in ﬂexure but not to translate), the critical longitudinal torsion on the shaft is found to be

critical

2EI

(24.14)

The nomenclature is the same as the preceding. The resulting shape upon buckling is a spiral with orthog-

onal deﬂections described by sinusoids. Shaft buckling would not be typically found in a free link but may

occur with the transmission of torque from motor to joint.

Other cases where torsion could be involved in link buckling are lateral-torsional buckling and ﬂexural-

torsionalbuckling.These failures arebecause of a reductionof ﬂexuralstiffnessresultingfroma longitudinal

rotation of the cross section [4]. A cross section with a large discrepancy between the area moments about

orthogonal directions is most susceptible to this type of failure.

24.2.2 Kinematics

Kinematics will be developed using 4 × 4 transformation matrices as frequently found in robotics. The

relation between positions and velocities is critical to developing dynamic equations and commanding

and controlling the joints to achieve desired end effector position. Two classes of relative motion will be

considered: discrete joints and distributed deﬂection.

24.2.2.1 Transformation Matrices

The commonly used 4 × 4 transformation matrices relate the position of a point as described in two

coordinate frames as detailed elsewhere in this book. For the immediate purposes, the nomenclature

relating the x, y, z values of two position vectors p

and p

is clariﬁed by

= T

(24.15)

= [

]

Note that the superscripts on position vectors and scalars represent the frame of reference in which the

position is described.

The transformation matrix T

can represent a variety of static or dynamic features of the mechanism

to which the coordinate frames are attached. For rigid links the key features are the relative location and

orientation of joint axes due to construction or motion of the joints. The strategy for efﬁciently locating

and describing the coordinate frames is described elsewhere in this handbook or in Sciavicco and Siciliano

[5], a slight variation of Craig [6], and is based on the original scheme proposed by Denavit and Hartenberg

[7]. For ﬂexible links, the features will include deﬂection under static or dynamic loads which we will focus

on in this section as employed by Book [8].

The core concept is the composition of the 4 ×4 transformation matrix as







000







(24.16)

isa3×3 rotation matrix describing rotations of the coordinates.













-10 Robotics and Automation Handbook

is the translation of the frame origin from i to j in j coordinates. The subscripts of the matrices, vectors,

and scalars identify the point of interest.

24.2.2.2 Simple Kinematic Pairs

For the intentional joints of a robot we can use the tools described for rigid robots. Rotational joints

introduceterms in the rotation matrix R

that varyas the joint anglechanges. Translational joints introduce

terms in the translation vector of the matrix T. The orientation of the joint axes and their distance of

separation (in terms of a common normal) appear as constant terms. The reader is referred to other

chapters for the development of these terms.

24.2.2.3 Closed Kinematic Chains

The serial connection of linkages is readily described by a chain of transformation matrices multiplied

together. If the series reattaches to itself, a closed chain is formed. The chain can also branch into multiple

series of linkages, which is often the case when a closed chain is introduced so that a distant joint can

be actuated with a stationary actuator. The additional constraints that are created by these topologies

can be readily described by consistently following a chain to the point of rejoining itself, describing each

successive transformation with a transformation matrix, and ultimately relating the initial coordinate

frame to itself. This constraint system may enhance the behavior of a compliant manipulator arm. Details

of these procedures are not included here.

24.2.2.4 Kinematics of Deformation

When a transformation describes deﬂection, the terms of the T transformation matrix are dependent on

loading and on the geometry of the component which is under deformation. The deformation may be

large or small, but the most common and useful case is the small deformation case. With small rotations

the rotation matrix of direction cosines can be simpliﬁed by considering only ﬁrst order terms composed

of the angles , ,  about X, Y, and Z, respectively, equivalent to the roll, pitch, and yaw rotations. Note

that for small angles the order of rotation is irrelevant. Hence







cos(x

) cos(y

) cos(z

) δx

cos(x

) cos(y

) cos(z

) δy

cos(x

) cos(y

) cos(z

) δz

0001







, T

∼







1 −δx

 1 −δy

− 1 δz

0001







(24.17)

The deformation of a beam with bending and torsion, for example, would use the deformations for the

bending for δy, δz, , and  and the equation for torsion for . δx would be zero unless compression of

the beam is considered, although this deﬂection is typically small.

When moving from one point on an arm to another, it is convenient to break the transformations into a

rigid transformation A

and an elastic transformation E

. The elastic transformation is small, as described

above, and dependent on loading. The combined effect is the multiplication of the two transforms. If the

typical slender linkage of an arm is envisioned, the elastic transformation due to bending, torsion, and

compression of relatively small amounts will be well described by







1 −α

θ Fi

− α

θ Mi

−α

θ Fi

+ α

θ Mi

θ Fi

+ α

θ Mi

1 −α

Xii

XFi

+ α

XMi

θ Fi

− α

θ Mi

1 α

XFi

+ α

XMi

00 01







(24.18)

Flexible Robot Arms 24

-11

where

=coefﬁcient in compression, displacement/force

=coefﬁcient in torsion, angle/moment

θFi

=coefﬁcient in bending, angle/force

θMi

=coefﬁcient in bending, angle/moment

XFi

=coefﬁcient in bending, displacement/force

XMi

=coefﬁcient in bending, displacement/moment

=force at the end of link i in the X direction of coordinate frame j

=force at the end of link i in the Y direction of coordinate frame j

=force at the end of link i in the Z direction of coordinate frame j

=moment at the end of link i in the X direction of coordinate frame j

=moment at the end of link i in the Y direction of coordinate frame j

=moment at the end of link i in the Z direction of coordinate frame j

Note that for readability we have assumed that the beam has a symmetrical cross section and the coefﬁcient

of F

is the same as the coefﬁcient of F

. In general these coefﬁcients could be distinct. The numerical

values for the simple and useful case of a uniform beam are found in the discussion of bending, torsion,

and compression above in Equation (24.2), Equation (24.3), and Equation (24.11).

After deformation the position of the arm’s tip, located at the origin of the nth coordinate frame, is

found as

= [A

···A

i+1

···A

]













(24.19)

24.2.3 Dynamics

In moving from kinematics to dynamics, we consider the relationship between forces and motion, that

is, the change in position over time. For rigid robots this primarily involves actuator forces and torques,

inertia acceleration or kinetic energy storage, frictional dissipation, and possibly gravity or other body

forces. For ﬂexible robots, the storage of potential energy in elastic deformation becomes important.

One of the early decisions on modeling the dynamics is how the kinetic and elastic potential energy

storage are to be spatially distributed. If predominantly separated in lumped components, the separate

modeling of springs and inertias will lead directly to ordinary differential equations. If these storage

modes are combined throughout the links, the lumped model is inefﬁcient and unsystematic, and the

partial differential equations or at least the distributed nature of the bodies should be considered.

24.2.3.1 Lumped Models

Lumped arm models will consider the arm to be made up of inertias and springs. The focus in this section

will be the linear behavior resulting from small motions consistent with the modeling of a structure

as an elastic member. The reader may be concerned with the choice between lumped and distributed

models. Lumped models are approximations that offer convenience, a more intuitive understanding and

simpler solution procedures at the cost of accuracy and/or computational efﬁciency. Components that

predominantly store potential energy as a spring with minimum storage of kinetic energy (due to low

mass or small velocities) are candidates for representation as a lumped spring. In contrast, components

storing kinetic energy with minimum compliance are candidates for lumped inertias. Because structural

materials intrinsically have both properties, the lumped approximation is never perfect.

-12 Robotics and Automation Handbook

Dissipation effects also warrant modeling. It is typically possible to include friction or viscous damping

into either the actuator forcing or to incorporate these losses into the equations for either lumped or

distributed models using the variables that are dictated by the mass and compliance representations.

24.2.3.1.1 Lumped Inertia

The deﬁnition of inertia could be approached from the distribution of mass and consequently a triple

integral over the volume of the body. For our purposes it will be more direct to deﬁne the inertia as the

matrix coefﬁcient that relates accelerations (translational and rotational) to forces and moments:











(24.20)

While not speciﬁc in the equation above, the usual reference point for writing these equations will be the

center of mass of the body and the motion will be relative to an inertial reference frame.

24.2.3.1.2 Lumped Springs

Springs are often visualized as a machine element intended to deform under load. More generally, any

real machine element will deform to a limited extent, and we should be much more inclusive in our

consideration of springs. For robots and other mechanisms there are machine elements that consistently

behave as unintentional springs: Shafts for transmission of power by rotation, bearings and bearing

housings, gear and other speed reducers, belts for transmission of power, and couplings. These and other

elements may be constrained in their cross section and hence are allowed to deform because the space

constraints do not permit an adequate stiffness.

It is tempting to enlarge the components that are not constrained in cross section. This mistake is often

observed in robot arm design and in machine design in general. In arms, an external beam member will

be increased in size and inertia making it very nearly rigid, while aggravating the lack of rigidity of the

constrained components that move it: shafts, bearings, joint structures, etc., as well as the links and drive

motors inboard of the oversized link. Structural natural frequency is a good indicator of the ﬂexibility

problem that ensues, and that natural frequency is predicted by the square root of the ratio of spring

constant over inertia. Increasing the cross section of an outboard component will continue to increase

inertia after its value in increasing stiffness of the chain of components has diminished. Because these

elements are more difﬁcult to analyze, the tendency is to over design them to approximate rigidity. For

this reason, considerable attention will be given to analysis of the compliance and distributed ﬂexibility of

the beam type elements of an arm’s construction.

24.2.3.1.3 Stiffness of a Series of Links

To evaluate the compliance of a series of N links to forces on the end of the chain, the partial derivative of

the position of the end can be taken, yielding, in the example case of F

∂p

∂ F





i=1

···A

∂ E

∂ F

i+1

···A















(24.21)

Similar expressions result for all six forces and moments on the arm’s end.

To complete this calculation numerically, note that

∂ E

∂ F

∂ E

∂ F

(24.22)

Flexible Robot Arms 24

-13

which can be obtained from the vector form



∂

∂ F

∂

∂ M

















× R

0 R



(24.23)

and from substitution into the equation for E

the value F

=1 and the value zero for all other forces

and moments. That is,

∂ E

∂ F







1 −α

θ Fi

− α

θ Mi

−α

θ Fi

+ α

θ Mi

θ Fi

+ α

θ Mi

1 −α

Xii

XFi

+ α

XMi

θ Fi

− α

θ Mi

1 α

XFi

+ α

XMi

00 01







(24.24)

where

= 1, F

= F

= 0, M

= M

= 0

The vector and scalar forms of forces F , moments M, positions X, and angles  are distinguished by

having only the single subscript indicating the link index. The expressions for all other forces and moments

are found equivalently and the lot assembled into a compliance matrix C, the inverse of the spring constant

matrix K

= C

−1

according to

C =



∂

∂ F

∂

∂ M

















(24.25)

Knowledge of the spring constant and the rigid body inertias is all that is needed to specify the equations of

motions of the lumped parameter ﬂexible link system if the joints are ﬁxed. As will be seen in the following

section, the approach above is also useful if the joints are controlled to move the arm.

24.2.3.2 Dynamics of Lumped Masses and Massless Elastic Links

with Servo Controlled Joints

For some applications of lightweight manipulators, particularly in space where a gravity load need not be

supported, very light links can be used to position large inertias. The Space Shuttle RMS and the Space

Station Arm are excellent examples of this situation. In these cases, the joints function to deform the links

(springs) which then apply forces and moments to the essentially rigid masses comprising the vehicle and

the payload. The following approach applies directly to that case and can be modiﬁed to apply to other

cases. For a more complete development see Book [8].

The kinematic relationships will be analyzed using transformation matrices consisting of

= rotation matrix from system i to system j

= distance vector from the origin of system i to the end of the chain (origin of system N)interms

of coordinates j

We will consider small translations and rotations of the two masses on either end, which will be described

by the vectors





, Z





(24.26)

where d

, d

are the position vectors from the origin of −1 (inertial frame) to the origins of 0 and n,

respectively, and 

, 

are the vectors of small rotations of mass 0 and n, respectively, from an initial

undeformed orientation.

-14 Robotics and Automation Handbook

In the case of joint angle rotations, the rotation will be permitted only about either the Z or the X axes.

The angles of rotations are:

= angle from positive Z

i−1

to positive Z

, measured counterclockwise about positive X

= angle from positive X

i−1

to positive X

measured counterclockwise about positive X

Joint position and rate control will be employed so that

Torque by actuators = K

(θ

− θ

) + D

(

−

)

where

=vector of m controlled joint angles measured from an arbitrary reference point

=vector of m desired joint angles

=vector of m controlled joint angular velocities

=vector of m desired joint angular velocities

=m × m matrix of position control gains

=m × m matrix of velocity control gains

The displacement of the end mass gives forces on that mass of



Forces

Moments



on mass at n

n displaced

=−K

− Z

) (24.27)

while that same force gives torques on the actuators of



Torques on actuators

with n displaced



= HK

− Z

) (24.28)

We will construct the matrix H element by element depending on the actuated joint, ﬁrst deﬁning the

cross product term

XCR

= r

× R

And the element notation H(i, j) = element in ith row, jth column of H,1≤ i ≤ m,1≤ j ≤ 6.

H(i, j ) =XCR

(k, j), 1 ≤ j ≤ 3, 1 ≤ i ≤ m

H(i, j ) = R

(k, j − 3), 3 ≤ j ≤ 6, 1 ≤ i ≤ m

where

k =1ifγ

is the ith element of θ

k =3ifβ

is the ith element of θ

m =total number of controlled joints

The following transformation will also be needed since rotations will also cause translations at a distant

point.



IXC

0 I



− Z

) = T

− Z

) (24.29)

XC =







0 −r

Z0n

Y0n

Z0n

0 −r

X0n

−r

Y0n

X0n







(24.30)