Kuppan T. Heat Exchanger Design Handbook
Подождите немного. Документ загружается.


454
Chapter
10
support configurations are (a) scalloped bars, (b) wiggle bars, (c) lattice bars, and (d) flat
bars, and they are as shown in Fig.
20
[41].
Tubes are likely to be under some axial loading as a result of fabrication and operation.
Tensile stresses increase the natural frequency, whereas compressive stress decreases the
natural frequency. Since axial compressive stress in the tube decreases the tube natural
frequency, rolling-in of the tubes in to the tubesheet should be done carefully. Care should
be also taken to allow for the free thermal expansion of the tubes. When significant com-
pressive axial loads are induced on the tubes in a multipass exchanger, these tubes shdl
be located in the baffle overlap regions to minimise the unsupported span length
[
1
11.
When only few tubes are exposed to high localized velocities, sealing strips may be applied
to provide flow resistance and reduce flow in critical areas
[74].
Plugging
of
Tubes.
The affected tubes may be omitted
or
plugged if proper precautions are
taken to ensure that collision will not endanger the adjacent tubes
[74].
Detuning
of
Tubes.
Detuning is defined as the method of producing differences among the
natural frequencies
of
the neighboring tubes in a tube array. The tubes are detuned by installa-
tion of additional supports such as clips, wedges, flat bars, helical spacers, strip baffles, or any
other means of increasing the tube fixity. Detuned tube arrays lose stability at a higher flow
velocity; the incidence
of
instability is more gradual in a tube bank with differences in
tube-
to-tube frequency than in a bank with identical tube frequency
[8].
Detuning
Eflect.
For the displacement mechanism associated with the coupled motion
of
adjacent tubes, detuning will have a significant effect, whereas for the velocity mechanism the
effect is little since the individual tube motion is independent of neighboring tubes and the
instability is controlled by fluid damping forces
[%I.
Lever and Weaver
[43]
found that for
air flow, detuning of neighbouring tubes produced a maximum increase in critical velocity
about
40%
at a frequency difference of
3%.
For frequency differences greater than about
10%,
there was no significant improvement in threshold instability. Tanaka et al.
[46]
report detuning
has increased the critical velocities for air flow by about
60%.
Avoid longer unsupported tube spans. Follow maximum unsupported tube length as speci-
fied in
TEMA,
RCB-4.52
[
191.
Figure
20
U-bend
supports.
Weaver
et
al.
[41].

455
Flow-
Induced
Vibration
Figure
21
Impingement plate protection. After Ref.
(19).
7.2
Methods to Decrease Crossflow Velocity
The following methods may be employed to reduce the crossflow velocity, which in turn will
decrease the vibration excitation potential.
1.
Reduce the crossflow velocity either by decreasing the flow rate or by increasing the
shell diameter. However, this will reduce the heat transfer rate. Even though testing has
indicated that controlling an instability usually requires lowering of the flow rate below
its initial threshold value, hysteresis suggests that instability may be initiated by flow
pulses that are caused by operational transients. Hence, while evaluating the critical ve-
locity, if such operational transients are anticipated, it may be desirable to reduce the
allowable flow rate significantly below the instability threshold [74].
2.
Increase the tube pitch such that crossflow area is increased. However, this will be at
the cost of lower shell-side heat transfer.
3.
If vibration damage to the tubes located beneath the nozzle is predicted, increase the
nozzle openings to decrease the mass velocity or install impingement plates as shown in
the Fig.
2
1.
4. If the vibration potential is predicted in the middle zone of an
E
shell, change the shell
design into either an
X
shell or
J
shell. Theoretically speaking, for the same mass flow
rate, the crossflow velocity on the shell side of a
J
shell will be half that of the
E
shell
Wl.
5.
Use double or multiple segmental baffles as shown in Fig.
22
to divide the flow into two
or more streams. In an exchanger with single segmental baffles the total flow, except for
leakages and bypass streams, passes through the tube bank between baffles (Fig.
23),
whereas in an exchanger with double segmental baffles barring the leakages, the flow
divides into two streams on either side of the shell, and into three streams in triple
segmental baffles. Under ideal conditions the crossflow velocity in a double segmental
baffles unit is half that of a comparable single segmental baffles units and one third with
triple segmental baffles. Hence, it is expected that double segmental baffles will double
the critical velocity compared to single segmental baffles. However, experiments on an
DOUBLE
SEGMEJVAL
64FFLES
Figure
22
Double segmental baffle design.
456
Chapter
I0
SINGLE
SEGMENTAL
B4FFLES
Figure
23
Fluid flow through single segmental baffle
unit.
industrial size heat exchanger at Argonne National Laboratory
[76]
show that the thresh-
old velocity increased by
24-67%.
The full theoretical potential of approximately dou-
bled threshold velocities was not realized. This was attributed to the effects of localized
end zone conditions, which were probably not eliminated.
6.
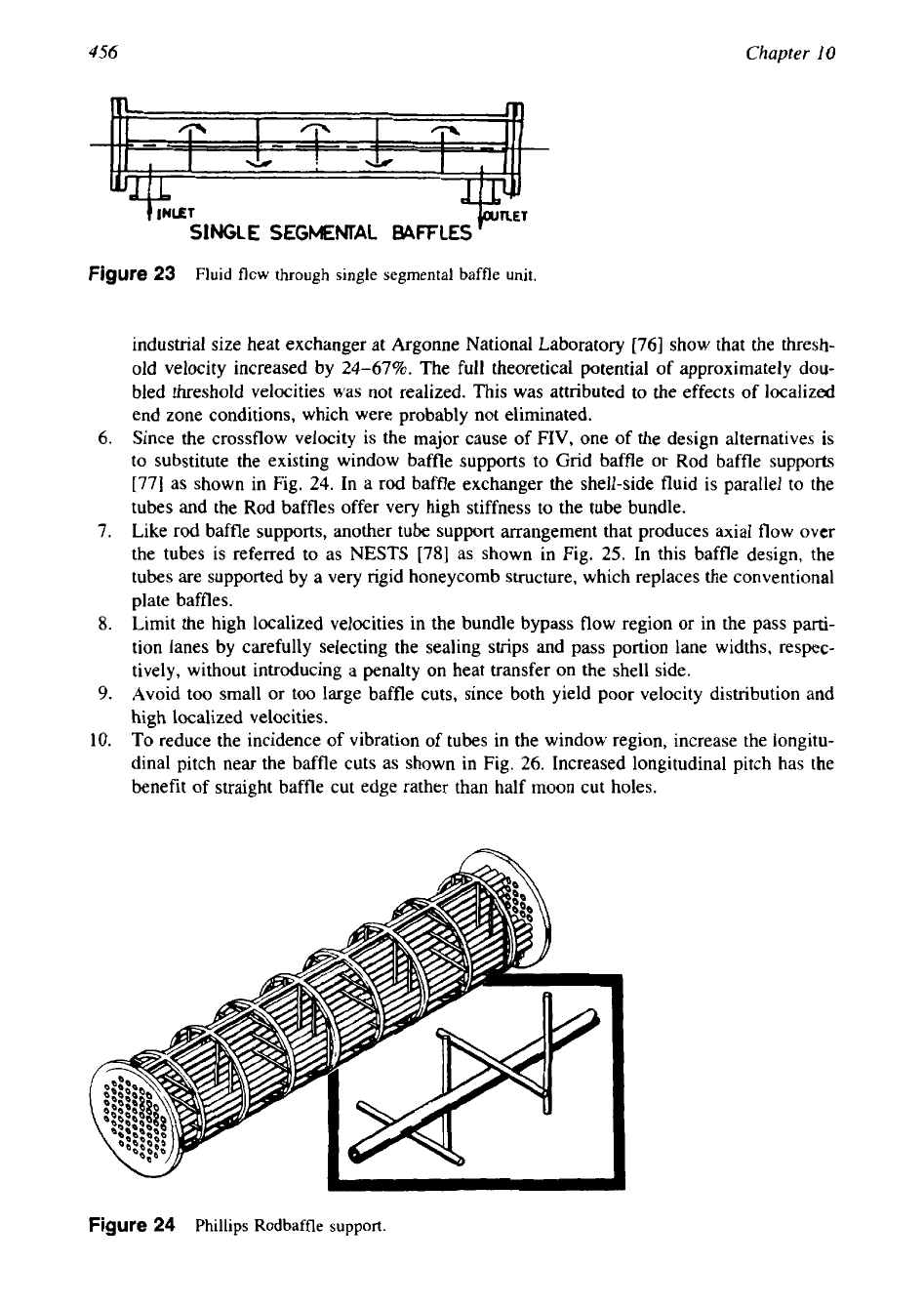
Since the crossflow velocity is the major cause of FIV, one of the design alternatives
is
to substitute the existing window baffle supports to Grid baffle or
Rod
baffle supports
[77]
as shown in Fig.
24.
In a rod baffle exchanger the shell-side fluid is parallel to the
tubes and the
Rod
baffles offer very high stiffness to the tube bundle.
7.
Like rod baffle supports, another tube support arrangement that produces axial flow over
the tubes is referred to as
NESTS
[78]
as shown in Fig.
25.
In this baffle design, the
tubes are supported by a very rigid honeycomb structure, which replaces the conventional
plate baffles.
8.
Limit the high localized velocities in the bundle bypass flow region or in the pass parti-
tion lanes by carefully selecting the sealing strips and pass portion lane widths, respec-
tively, without introducing a penalty on heat transfer on the shell side.
9.
Avoid too small or too large baffle cuts, since both yield poor velocity distribution and
high localized velocities.
10.
To
reduce the incidence of vibration of tubes in the window region, increase the longitu-
dinal pitch near the baffle cuts as shown in Fig.
26.
Increased longitudinal pitch has the
benefit of straight baffle cut edge rather than half moon cut holes.
Figure
24
Phillips Rodbaffle support.
457
Flow-Induced
Vibration
Figure
25
NESTm
tube support arrangement. After Boyer et al.79.
a
lncreoscd
longitudinol
pitch
b
Figure
26
Baffle cut schemes. (a) Typical baffle cut (half
moon);
and
(b)
discontinuous longitudinal
pitch at baffle cut, (From Ref.
11
.)

458
Chapter
10
11. Maintain small tube to baffle hole clearances; follow TEMA Standard RCB-4.2
[
191.
12. Ensure uniform baffle spacings.
7.3
Suppression
of
Standing Wave Vibration
The acoustic standing waves can be suppressed by any of the following devices or methods:
1.
Antivibration baffles (AVB), solid or porous baffle
2.
Re sonat ors
3.
Fin barriers
4.
Helical spacers
5.
Detuning or structural modification
6.
Removal of tubes
7.
Surface modification
8.
Irregular lateral spacing of tubes
9.
Changing the mass flow rate
Antivibration Baffles
Solid
Bafle.
The occurrence of acoustic resonance in a crossflow heat exchanger is related
to the development of standing waves. If the standing waves are inhibited from developing,
then the associated acoustic resonance will not take place. This is achieved by incorporation
of either
a
solid baffle or porous baffle inside the heat exchanger, in a direction parallel to the
flow and perpendicular to the direction of standing waves. The baffles are also called detuning
baffles. The placement of solid baffles
is
shown schematically in Fig.
27.
Number of Solid Baffles. As per theory,
if
solid baffles are to be installed
in
a tubular
heat exchanger
in
which the maximum number of half-waves that can occur between the walls
is
N,,,
then
N,
solid baffles should be installed to prevent the acoustic vibration. The major
drawback associated with the solid baffles is that the number of baffles required is very high
for a heat exchanger of spatial size of
20-30
m used in the fossil fuel utilities, like an econo-
mizer, reheater, etc. However, the number of baffles requirement can be minimised by follow-
ing Chen’s method
[25].
The method consists of placing solid baffles
in
preferred locations as
shown
in
Fig.
28.
The distances
b,, bZ,
b3,
b4, b5,
and
6,
are all to be kept different from each
other and their ratios
b,lb,,
b41b3,
and
b6/bs
should deviate much from the integers correspond-
ooooog
000
=+
O
WsX!
H H
000000
h
888
000
8888888
000000
8
8 8
8
8 8
g--
0000000
Figure
27
Detuning solid baffle arrangement. (a) Central baffle; (b) upstream baffle;
(c)
downstream
baffle; and (d) two baffles at
1/3
and
2/3
transverse locations. (From Ref.
61.)

459
Flow-Induced
Vibration
Figure
28
Chen’s method of solid baffle arrangement. Insertion
of
the slightly overlapped detuning
baffles into the heat exchanger
to
make the natural frequencies
of
the transverse gas columns in the
spaces,
b,, b?,
b3,
b4,
bs,
and
bh
as
different as possible from one another. (From Ref.
25.)
ing to the modes of the vibrations to be expected. While placing the baffles the length of the
baffle should be large in comparison with the wavelength of the standing waves to be expected
in
the heat exchanger. The shortcomings associated with the solid baffles are discussed by
Eisinger
[57].
They include these:
1.
Expensive for retrofitting
2.
Inhibition of periodical inspection and maintenance operations
3.
Limited life
if
the medium of flow is corrosive in nature
4.
Tendency to vibrate and susceptible to thermal distortion
in
service
Porous
Bafle.
The
porous baffle concept consists
of
a
single flow-resistive element inserted
between the tubes
so
that it is parallel to the flow direction
[79].
Byrne
[79]
has shown that,
in general, if the maximum number of half-waves between the walls
is
Nu,
then a single porous
baffle should be located at a distance from one wall equal to the wall-to-wall span divided by
2N,,.
The advantage of a porous baffle over that
of
solid baffles is that a single porous baffle
can be used to inhibit the development
of
a number
of
standing waves, whereas the number of
solid baffles required is equal to the maximum number of half-waves that can develop between
the walls.
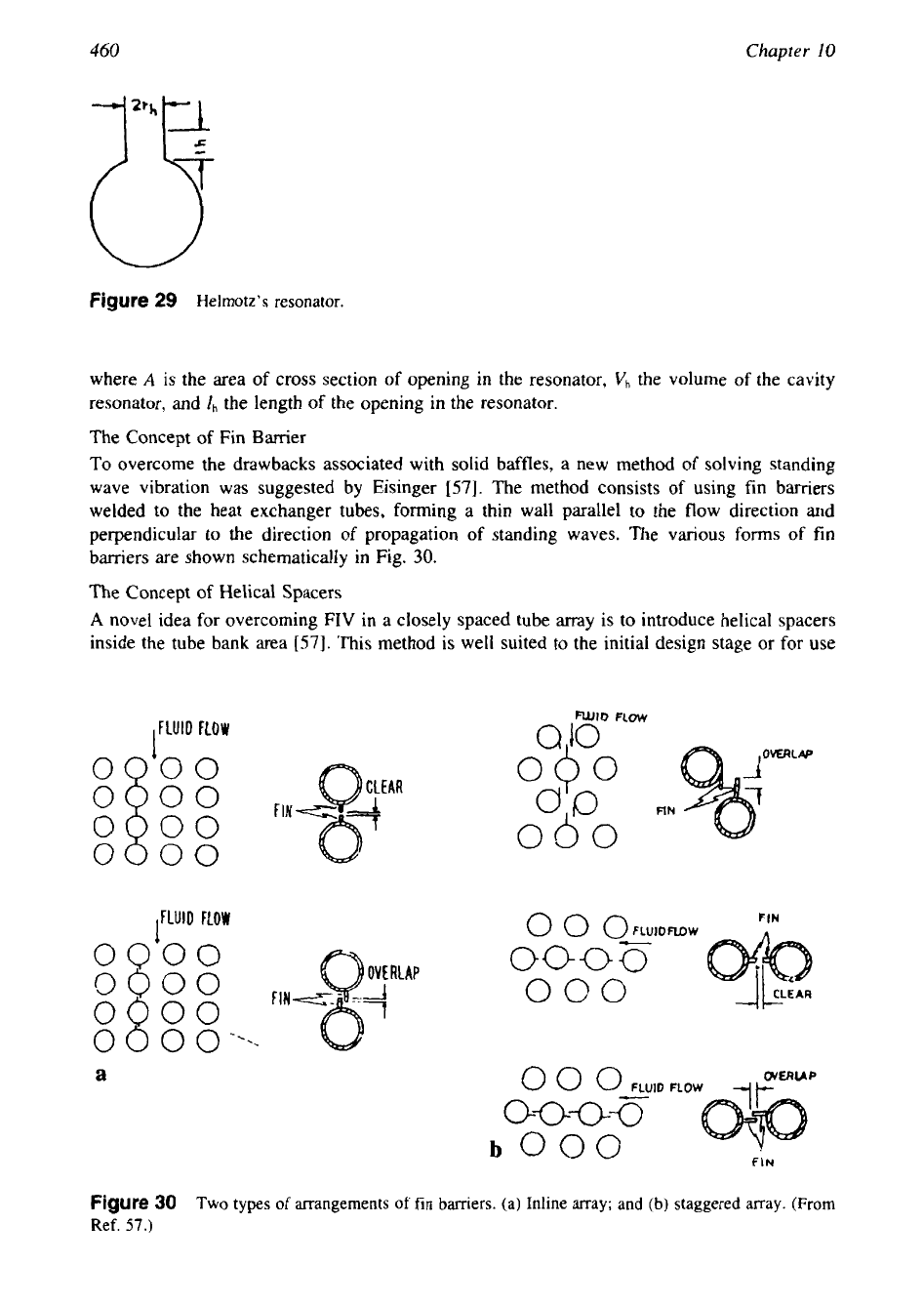
Helmhotz Cavity Resonator
Installation of an acoustic damper such as a tuned Helmhotz cavity resonator on the shell side
will suppress the acoustic vibration. A simple Helmhotz resonator is shown in
Fig.
29.
The
damping is maximum when the resonator is tuned with the acoustic mode of interest
[62].
When tuned, there is a large oscillating mass flow through the resonator neck which expends
energy by passing through the neck and/or the screen placed
in
the neck. An approximate
formula for the resonator natural frequency is given by
[62]:
460
Chapter
10
Figure
29
Helmotz’s resonator.
where
A
is the area
of
cross section
of
opening in the resonator,
Vh
the volume
of
the cavity
resonator, and
I,
the length
of
the opening in the resonator.
The Concept
of
Fin Barrier
To
overcome the drawbacks associated with solid baffles, a new method
of
solving standing
wave vibration was suggested by Eisinger
[57].
The method consists of using fin barriers
welded
to
the heat exchanger tubes, forming a thin wall parallel to the flow direction and
perpendicular to the direction
of
propagation
of
standing waves. The various
forms
of
fin
barriers are shown schematically in Fig.
30.
The Concept
of
Helical Spacers
A
novel idea for overcoming
FIV
in a closely spaced tube array is to introduce helical spacers
inside the tube bank area
[57].
This method is well suited to the initial design stage
or
for use
WtD
FLOW
,FLUID
FLOW
EAR
FIN
obo
lFLUlO
0000
0000
FIN
0000
0000-.
a
Figure
30
Two
types of arrangements
of
fin barriers. (a) Inline array; and
(b)
staggered array. (From
Ref.
57.)

461 Flow-Induced Vibration
in field modifications. The method is applicable both for staggered and in-line tube layout, and
spacer placement is shown schematically in Fig.
31.
Detuning
This has been already discussed.
Removal of Tubes
Selective removal of a few tubes at the displacement antinodes of the standing waves will
eliminate the vortex shedding and thus avoid the coupling between vortex shedding and acous-
tic resonance. This also upsets the vortex shedding regularity at pressure nodes. Walker and
Reising [80] and Barrington
[63,67]
have observed that by removing
3-10%
of
tubes near the
centre of the tube bank, acoustic resonance can be diminished or eliminated.
Surface Modification
Fouling of heat exchanger tubes by dirt and carbon soot has been associated with the reduction
in sound level, and hence the deposition increases the acoustic damping [8,81].
Irregular Spacing of Tubes
Destroy the phasing of vortex streets by having irregular spacing of tubes. This will scramble
the vortex shedding frequency. Zdravkovich and Nuttal [82] found the nonoccurrence
of
stand-
ing waves by displacing the susceptible tubes either laterally or longitudinally as shown in Fig.
26(b). However, this method is only attractive if the thermal performance is not affected.
Change the Mass Flow Rate
Modify vortex shedding frequency by changing the mass flow rate. This may not be very
attractive from a thermal performance
point of view.
D
Figure
31
Helical spacers in (a) staggered tube array; and (b) inline tube array.
(From
Ref.
57.)

462
Chapter
10
TUBE
SUPPOf7T
OIRECTION
1
UBE
OF
VIBRATION
Figure
32
Vibrating tube
in
baffle hole.
(From
Ref.
94.)
8
BAFFLE DAMAGE AND COLLISION DAMAGE
Empirical Checks for Vibration Severity
From the prevalent pattern of tube failures occurring at the baffle supports and at the midspan,
Thorngren
[83]
has attributed tube failures mainly to (1) baffle type damage and
(2)
collision
type damage. He proposed two empirical correlations, called baffle damage number,
NHL>,
and
collision damage number,
NcD,
to check the severity of tube damage due to
FIV.
The expres-
sions for these damage numbers can be easily deduced similar to Connor’s instability equation.
Therefore they are not discussed here.
9
IMPACT AND FRETTING WEAR
Heat exchanger tubes are supported at regular intervals by passing through oversized holes in
baffle plates (Fig.
32).
As
the tubes vibrate against the support plates, material can be fretting
away from both the tube and the support plate as shown in Fig.
33.
If the fretting wear of tube
is sufficiently large, the tubes will eventually rupture due to the fluid pressure
[38].
When one
considers that a design objective for a nuclear power plant steam generator or a heat exchanger
is a
40
years codal life, even relatively small tube wear rates cannot be tolerated
[6,38].
Hence
in
recent years significant attention has been given to study the effect of tube-to-tube support
plate clearances on tube vibration and wear,
by
(1) laboratory experiments,
(2)
theoretical
@
BAFFLE
DAMAGE:
@
COLLISION
DAMAGE
Figure
33
Fretting wear of tubes.

Flow-Induced
Vibration
463
simulations, and (3) analytical models. Vibration excitation mechanisms responsible for fretting
wear are (1) vortex shedding,
(2)
turbulent buffeting, and
(3)
fluid elastic instability. Refer-
ences 38 and 84-93 brought about a greater understanding of the tube-to-tube support plate
interaction characteristics and resultant tube wear.
9.1
Tube Wear Prediction by Experimental Techniques
Among the experimental techniques, the notable are that of Blevins [84,85], and Haslinger et
al. [86]. The fundamental assumption of the Blevins [84] experimental fretting wear model is
that fretting wear is the result of relative motion between the tube and the support plates.
Blevins assumed that the fretting wear is a function of parameters such as
(1)
tube geometry,
(2) baffle plates geometry,
(3)
tube and baffle plate material properties, (4) amplitude, fre-
quency and mode shape of tube vibration,
(5)
preload between the tube and support plate, and
(6) nature of environment and operating temperature.
Recently, Blevins [94] conducted experiments to predict wear induced by vibration on a
heat exchanger model with alloy 800H and 2.25Cr-1Mo steel heat exchanger tubes loosely
held supports
in
a helium environment at temperatures up to
650°C
(1200°F).
From the conclu-
sions derived from his experiments, it is seen that
(1)
impact wear can be minimized by
reducing the impact contact stresses below the fatigue allowable stress,
(2)
decreasing the
vibration amplitude or baffle hole clearance markedly decreases wear rate and subsurface de-
formation at all temperatures, and
(3)
application of chromium coating both to the tube and
the plate specimens greatly reduces the surface self-adhesion and surface deformation that
would otherwise occur above
500°C
(930°F). Below this temperature, a coating is probably
not required.
9.2
Theoretical Model
Nonlinear finite-element modeling techniques to predict tube wear due to turbulence excitation,
fluid elastic instability, or vortex shedding are discussed in refs. 38 and 89-93. The wear
parameters central for the theoretical models are
(1)
sliding distance,
(2)
contact time, (3)
average contact time, (4) threshold crossings, and
(5)
work rate.
10
DETERMINATION
OF
HYDRODYNAMIC MASS, NATURAL
FREQUENCY, AND DAMPING
Flow-induced vibration analysis of heat exchangers require the knowledge of damping, hydro-
dynamic mass, and natural frequency of tube bundle. Their determination is discussed next.
10.1
Added
Mass
or
Hydrodynamic
Mass
During flow-induced vibration, the vibrant tubes displace the shell-side fluid. When the fluids
involved are liquids or very dense gases, the inertia of the fluid will have substantial effect on
natural frequency of the tubes. Hence, while calculating the natural frequency of the tube, the
influence
of
the displaced fluid is taken care
of
by augmenting the mass of the vibrating tube
by including hydrodynamic mass or added mass. The added mass is defined as the displaced
fluid mass times an added mass coefficient
C,.
Since the added mass augments the vibrating
tube mass, the natural frequency of the tube will be reduced compared to when the tube is
vibrating in vacuum or very low density gas.
