Куликов А.А. (сост.) Смешанные задачи для уравнения теплопроводности и уравнения колебаний
Подождите немного. Документ загружается.

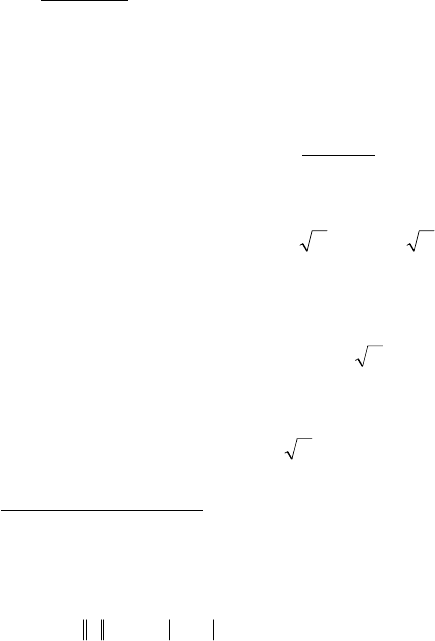
31
ɛ)
000
1
c
)(Xh)(X ,
0
)
l(
X
( 0
1
!
h );
III. ɚ)
00
)
(
X
, 0
c
)
l(
X
; ( 0
2
h );
ɛ)
00
)
(
X
,
0
2
c
)l(Xh)l(X
(
0
2
!
h
)
IV. ɚ)
00
c
)
(
X
,
0
c
)
l(
X
( 0
21
hh );
ɛ)
00
c
)
(
X
, 0
2
c
)l(Xh)l(X ( 0
1
h , 0
2
!
h );
ɜ)
000
1
c
)(Xh)(X
, 0
c
)
l(
X
(
0
1
!
h
,
0
2
h
);
ɝ)
000
1
c
)(Xh)(X , 0
2
c
)l(Xh)l(X
(
0
1
!
h , 0
2
!
h ).
ɉɪɢɦɟɪ 1
. ɇɚɣɬɢ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ, ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ ɢ
ɤɜɚɞɪɚɬɵ ɧɨɪɦ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ
1
ɜ ɡɚɞɚɱɟ ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ ɫ ɝɪɚ-
ɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ I:
00
)
(
X
, (6.18)
0
)
l(
X
. (6.19)
Ɋɟɲɟɧɢɟ
ȼ ɫɢɥɭ ɫɜɨɣɫɬɜɚ 6 ɜɫɟ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ
O
ɩɨɥɨɠɢɬɟɥɶɧɵ.
Ɉɛɳɟɟ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (6.1) ɩɪɢ
0
!
O
ɢɦɟɟɬ ɜɢɞ
xBxA)x(X
OO
sincos
, (6.20)
ɝɞɟ
A ɢ B – ɩɪɨɢɡɜɨɥɶɧɵɟ ɩɨɫɬɨɹɧɧɵɟ.
ɇɚɣɞɟɦ ɧɟɬɪɢɜɢɚɥɶɧɵɟ ɪɟɲɟɧɢɹ ɜɢɞɚ (6.20), ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɟ ɭɫɥɨ-
ɜɢɹɦ (6.18), (6.19). ɂɡ (6.18) ɫɥɟɞɭɟɬ, ɱɬɨ
0
A
, ɢ, ɬɚɤɢɦ ɨɛɪɚɡɨɦ,
xB)x(X
O
sin
;
ɩɪɢ ɷɬɨɦ
0
z
B .
ɂɫɩɨɥɶɡɭɹ ɬɟɩɟɪɶ ɭɫɥɨɜɢɟ (6.19), ɢɦɟɟɦ
0
l
O
sin . (6.21)
Ɂɧɚɱɟɧɢɹ
0
!
O
, ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɟ ɭɪɚɜɧɟɧɢɸ (6.21), ɬɨ ɟɫɬɶ
1
Ɂɞɟɫɶ ɢ ɜ ɞɚɥɶɧɟɣɲɟɦ ɩɨɞ ɧɨɪɦɨɣ ɮɭɧɤɰɢɢ ɢɡ )l,(L 0
2
ɩɨɧɢɦɚɟɬɫɹ ɟɟ ɧɨɪɦɚ ɜ ɞɚɧɧɨɦ
ɩɪɨɫɬɪɚɧɫɬɜɟ (ɡɚɦɟɬɢɦ, ɱɬɨ ɞɥɹ ɮɭɧɤɰɢɣ, ɩɪɢɧɚɞɥɟɠɚɳɢɯ ɬɟɦ ɢɥɢ ɢɧɵɦ ɩɨɞɦɧɨɠɟɫɬ-
ɜɚɦ ɦɧɨɠɟɫɬɜɚ )l,(L 0
2
, ɦɨɠɧɨ ɨɩɪɟɞɟɥɢɬɶ ɢ ɞɪɭɝɢɟ ɧɨɪɦɵ; ɧɚɩɪɢɦɟɪ, ɟɫɥɢ ɮɭɧɤɰɢɹ
)x(f
ɧɟɩɪɟɪɵɜɧɚ ɧɚ ɨɬɪɟɡɤɟ
],[ l0
, ɧɚɪɹɞɭ ɫ ɟɟ ɧɨɪɦɨɣ ɜ
)l,(L 0
2
ɦɨɠɧɨ ɪɚɫɫɦɚɬɪɢ-
ɜɚɬɶ ɧɨɪɦɭ
)x(ff
lx
C
dd
0
max
).
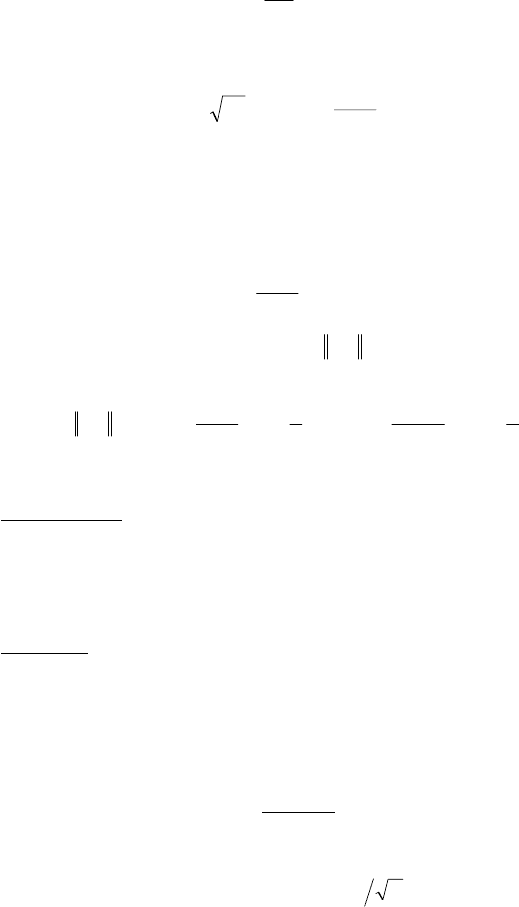
32
2
¸
¹
·
¨
©
§
l
n
n
S
OO
, !,, 21
n ,
ɹɜɥɹɸɬɫɹ ɢɫɤɨɦɵɦɢ ɫɨɛɫɬɜɟɧɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ. ɋɨɛɫɬɜɟɧɧɨɦɭ ɡɧɚɱɟɧɢɸ
n
O
ɨɬɜɟɱɚɟɬ ɫɨɛɫɬɜɟɧɧɚɹ ɮɭɧɤɰɢɹ
l
xn
BxB)x(X
nnnn
S
O
sinsin
, !,, 21
n ,
ɝɞɟ
0
z
n
B – ɩɪɨɢɡɜɨɥɶɧɚɹ ɩɨɫɬɨɹɧɧɚɹ.
Ɍɚɤ ɤɚɤ ɥɸɛɚɹ ɫɨɛɫɬɜɟɧɧɚɹ ɮɭɧɤɰɢɹ ɨɩɪɟɞɟɥɹɟɬɫɹ ɫ ɬɨɱɧɨɫɬɶɸ ɞɨ ɩɨ-
ɫɬɨɹɧɧɨɝɨ ɦɧɨɠɢɬɟɥɹ, ɨɬɥɢɱɧɨɝɨ ɨɬ ɧɭɥɹ, ɬɨ ɛɟɡ ɨɝɪɚɧɢɱɟɧɢɹ ɨɛɳɧɨɫɬɢ
ɦɨɠɧɨ ɫɱɢɬɚɬɶ, ɱɬɨ
1
n
B ,
!,, 21
n
.
ɂɬɚɤ, ɢɫɤɨɦɵɦɢ ɫɨɛɫɬɜɟɧɧɵɦɢ ɮɭɧɤɰɢɹɦɢ ɹɜɥɹɸɬɫɹ ɮɭɧɤɰɢɢ
l
xn
)x(X
n
S
sin
, !,, 21
n . (6.22)
Ⱦɥɹ ɮɭɧɤɰɢɣ (6.22) ɧɚɣɞɟɦ ɡɧɚɱɟɧɢɹ
2
n
X
, ɢɫɩɨɥɶɡɭɟɦɵɟ ɜ ɮɨɪɦɭɥɟ
(6.12):
2
2
1
2
1
00
2
2
l
xd
l
xn
xd
l
xn
X
ll
n
¸
¹
·
¨
©
§
³³
SS
cossin ,
!,, 21
n .
ɍɩɪɚɠɧɟɧɢɟ 3
. ɉɨɤɚɡɚɬɶ, ɱɬɨ ɪɚɡɥɨɠɟɧɢɟ ɮɭɧɤɰɢɢ
)
x
(
f
, ɭɞɨɜɥɟɬɜɨ-
ɪɹɸɳɟɣ ɭɫɥɨɜɢɹɦ ɬɟɨɪɟɦɵ ɋɬɟɤɥɨɜɚ, ɜ ɪɹɞ Ɏɭɪɶɟ (6.11) ɩɨ ɫɢɫɬɟɦɟ ɫɨɛɫɬ-
ɜɟɧɧɵɯ ɮɭɧɤɰɢɣ (6.22) ɫɨɜɩɚɞɚɟɬ ɧɚ ɨɬɪɟɡɤɟ
],[ l0
ɫ ɪɚɡɥɨɠɟɧɢɟɦ ɜ ɬɪɢɝɨ-
ɧɨɦɟɬɪɢɱɟɫɤɢɣ ɪɹɞ Ɏɭɪɶɟ ɧɟɱɟɬɧɨɝɨ ɩɪɨɞɨɥɠɟɧɢɹ ɷɬɨɣ ɮɭɧɤɰɢɢ ɧɚ ɨɬɪɟ-
ɡɨɤ
],[ ll
(ɫɦ., ɧɚɩɪɢɦɟɪ, [1, §55]).
ɉɪɢɦɟɪ 2
. ɇɚɣɬɢ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ, ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ ɢ
ɤɜɚɞɪɚɬɵ ɧɨɪɦ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɜ ɡɚɞɚɱɟ ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ ɫ ɝɪɚ-
ɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ II ɛ):
000
1
c
)(Xh)(X , 0
1
!
h , (6.23)
0
)
l(
X
. (6.24)
Ɋɟɲɟɧɢɟ
Ɍɚɤ ɠɟ, ɤɚɤ ɢ ɜ ɩɪɟɞɵɞɭɳɟɦ ɩɪɢɦɟɪɟ, ɜɫɟ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ
O
ɩɨɥɨɠɢɬɟɥɶɧɵ, ɢ ɨɛɳɟɟ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (6.1) ɞɚɟɬɫɹ ɮɨɪɦɭɥɨɣ (6.20).
ɂɫɩɨɥɶɡɭɹ ɭɫɥɨɜɢɟ (6.23), ɧɚɯɨɞɢɦ, ɱɬɨ
AhB
O
1
, ɢ, ɬɚɤɢɦ ɨɛɪɚɡɨɦ,
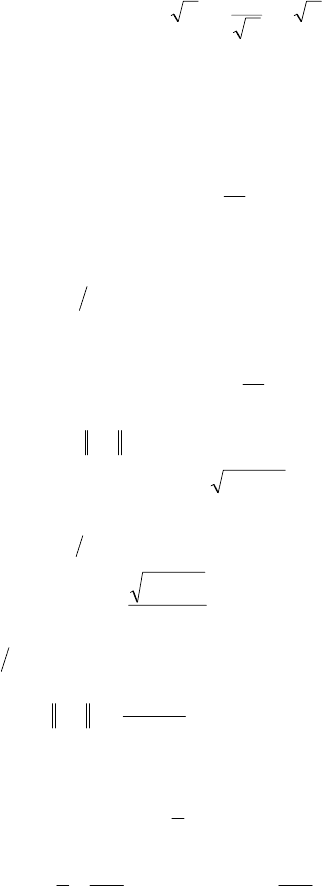
33
¸
¸
¹
·
¨
¨
©
§
x
h
xA)x(X
O
O
O
sincos
1
,
ɝɞɟ
A
– ɩɪɨɢɡɜɨɥɶɧɚɹ ɩɨɫɬɨɹɧɧɚɹ, ɨɬɥɢɱɧɚɹ ɨɬ ɧɭɥɹ. ȼ ɞɚɥɶɧɟɣɲɟɦ ɛɭɞɟɦ
ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ
1
A
.
ɂɫɩɨɥɶɡɭɹ ɬɟɩɟɪɶ ɭɫɥɨɜɢɟ (6.24), ɩɨɥɭɱɢɦ, ɱɬɨ ɢɫɤɨɦɵɦɢ ɫɨɛɫɬɜɟɧ-
ɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɹɜɥɹɸɬɫɹ ɜɟɥɢɱɢɧɵ
2
nn
W
O
, !,, 21
n , ɝɞɟ
n
W
– ɩɨɥɨ-
ɠɢɬɟɥɶɧɵɟ ɤɨɪɧɢ ɬɪɚɧɫɰɟɧɞɟɧɬɧɨɝɨ ɭɪɚɜɧɟɧɢɹ
1
h
l
W
W
tg (6.25)
(ɥɟɝɤɨ ɜɢɞɟɬɶ, ɱɬɨ ɭɪɚɜɧɟɧɢɟ (6.25) ɢɦɟɟɬ ɫɱɟɬɧɨɟ ɦɧɨɠɟɫɬɜɨ ɩɨɥɨɠɢɬɟɥɶ-
ɧɵɯ ɤɨɪɧɟɣ, ɹɜɥɹɸɳɢɯɫɹ ɚɛɫɰɢɫɫɚɦɢ ɬɨɱɟɤ ɩɟɪɟɫɟɱɟɧɢɹ ɝɪɚɮɢɤɨɜ ɮɭɧɤ-
ɰɢɣ
l
y
W
tg
ɢ
1
hy
W
).
ɋɨɛɫɬɜɟɧɧɨɦɭ ɡɧɚɱɟɧɢɸ
2
nn
W
O
ɨɬɜɟɱɚɟɬ ɫɨɛɫɬɜɟɧɧɚɹ ɮɭɧɤɰɢɹ
x
h
x)x(X
n
n
nn
W
W
W
sincos
1
, !,, 21
n . (6.26)
ɇɚɣɞɟɦ ɜɟɥɢɱɢɧɵ
2
n
X
,
!,, 21
n
. ɂɫɩɨɥɶɡɭɹ ɢɡɜɟɫɬɧɭɸ ɮɨɪɦɭɥɭ
)ȝĮ(baba
sinsincos
22
DD
,
ɝɞɟ
a ɢ b – ɩɪɨɢɡɜɨɥɶɧɵɟ ɜɟɳɟɫɬɜɟɧɧɵɟ ɤɨɷɮɮɢɰɢɟɧɬɵ, ɬɚɤɢɟ, ɱɬɨ
0
22
!
ba , ɢ ba
P
tg , ɡɚɩɢɲɟɦ ɮɭɧɤɰɢɸ )x(X
n
ɜɜɢɞɟ
)ȝxIJ(
h
)x(X
nn
n
n
n
sin
W
W
2
1
2
, !,, 21
n , (6.27)
ɝɞɟ
1
h
nn
W
P
tg . Ɍɨɝɞɚ
xd)ȝxIJ(
h
X
l
nn
n
n
n
³
0
2
2
2
1
2
2
sin
W
W
. (6.28)
Ⱦɚɥɟɟ,
> @
³³
xd)ȝxIJ(xd)ȝxIJ(
l
nn
l
nn
00
2
21
2
1
cossin
n
n
nn
n
ȝ)ȝlIJ(
l
2
4
1
2
4
1
2
sinsin
WW
. (6.29)
ɂɫɩɨɥɶɡɭɹ ɮɨɪɦɭɥɵ

34
D
D
D
2
tg1
tg
sin
2
2
,
ED
E
D
tgtg
tgtg
tg
1
)ȕĮ(
ɢ ɭɱɢɬɵɜɚɹ, ɱɬɨ
1
hl
nn
W
W
tg
(ɜ ɫɢɥɭ (6.25)) ɢ
1
h
nn
W
P
tg
, ɢɦɟɟɦ:
02
)ȝlIJ(
nn
sin
,
2
1
2
1
2
2
h
h
ȝ
n
n
n
W
W
sin , !,, 21
n . (6.30)
ɂɡ (6.28) – (6.30) ɫɥɟɞɭɟɬ, ɱɬɨ
2
1
2
1
2
2
2
n
n
n
hhl
X
W
W
, !,, 21
n .
ɉɪɢɦɟɪ 3
. ɇɚɣɬɢ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ, ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ ɢ
ɤɜɚɞɪɚɬɵ ɧɨɪɦ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɜ ɡɚɞɚɱɟ ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ ɫ ɝɪɚ-
ɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ IV ɚ):
00
c
)
(
X
, 0
c
)
l(
X
(6.31)
Ɋɟɲɟɧɢɟ
ȼ ɫɢɥɭ ɫɜɨɣɫɬɜɚ 6, ɜ ɡɚɞɚɱɟ ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ ɫ ɪɚɫɫɦɚɬɪɢɜɚɟɦɵɦɢ
ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ ɧɚɢɦɟɧɶɲɟɟ ɫɨɛɫɬɜɟɧɧɨɟ ɡɧɚɱɟɧɢɟ ɪɚɜɧɨ ɧɭɥɸ, ɢ
ɟɦɭ ɨɬɜɟɱɚɟɬ ɫɨɛɫɬɜɟɧɧɚɹ ɮɭɧɤɰɢɹ
0
z
{
const
)
x(
X
. ȼ ɞɚɥɶɧɟɣɲɟɦ ɛɭ-
ɞɟɦ ɨɛɨɡɧɚɱɚɬɶ ɭɤɚɡɚɧɧɨɟ ɫɨɛɫɬɜɟɧɧɨɟ ɡɧɚɱɟɧɢɟ ɱɟɪɟɡ
0
O
ɢ ɩɪɟɞɩɨɥɚɝɚɬɶ,
ɱɬɨ ɫɨɨɬɜɟɬɫɬɜɭɸɳɚɹ ɫɨɛɫɬɜɟɧɧɚɹ ɮɭɧɤɰɢɹ
1
0
{
)x(X .
ɂɫɩɨɥɶɡɭɹ ɮɨɪɦɭɥɭ (6.20) ɢ ɝɪɚɧɢɱɧɵɟ ɭɫɥɨɜɢɹ (6.31), ɧɚɯɨɞɢɦ ɩɨɥɨ-
ɠɢɬɟɥɶɧɵɟ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ ɢ ɨɬɜɟɱɚɸɳɢɟ ɢɦ ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ:
2
¸
¹
·
¨
©
§
l
n
n
S
O
,
l
xn
)x(X
n
S
cos
, (6.32)
ɝɞɟ
1
t
n
.
ȼɫɸ ɫɨɜɨɤɭɩɧɨɫɬɶ ɫɨɛɫɬɜɟɧɧɵɯ ɡɧɚɱɟɧɢɣ ɢ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɜ
ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɡɚɞɚɱɟ ɦɨɠɧɨ ɬɚɤɠɟ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ (6.32), ɩɪɟɞɩɨɥɚɝɚɹ,
ɱɬɨ
!210 ,,
n .
Ʌɟɝɤɨ ɜɢɞɟɬɶ, ɱɬɨ
lX
2
0
,
2
2
lX
n
ɞɥɹ !21,
n .
ɉɪɢɦɟɪ 4
. ɇɚɣɬɢ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ, ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ ɢ
ɤɜɚɞɪɚɬɵ ɧɨɪɦ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɜ ɡɚɞɚɱɟ ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ ɫ ɝɪɚ-
ɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ IV ɝ):
000
1
c
)(Xh)(X , 0
2
c
)l(Xh)l(X ,
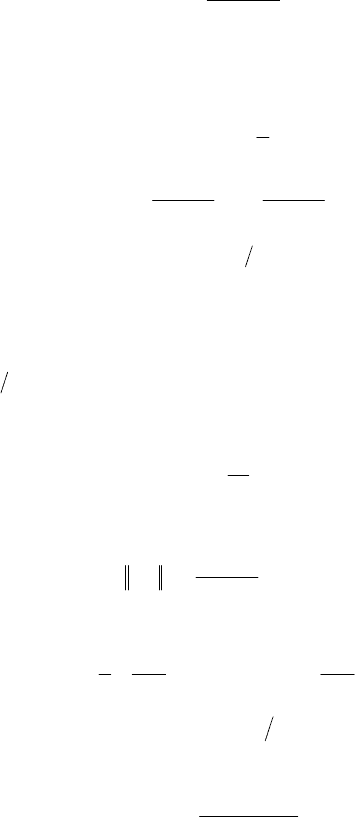
35
ɝɞɟ
0
1
!
h , 0
2
!
h .
Ɋɟɲɟɧɢɟ
ɂɫɩɨɥɶɡɭɹ ɬɟ ɠɟ ɪɚɫɫɭɠɞɟɧɢɹ, ɱɬɨ ɢ ɜ ɩɪɢɦɟɪɟ 2, ɩɨɥɭɱɢɦ, ɱɬɨ ɢɫɤɨ-
ɦɵɦɢ ɫɨɛɫɬɜɟɧɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɹɜɥɹɸɬɫɹ ɜɟɥɢɱɢɧɵ
2
nn
W
O
,
!,, 21
n
,
ɝɞɟ
n
W
– ɩɨɥɨɠɢɬɟɥɶɧɵɟ ɤɨɪɧɢ ɭɪɚɜɧɟɧɢɹ
W
WW
q
pl
ctg , (6.33)
21
1
hh
p
,
21
21
hh
hh
q
.
Ɂɚɦɟɬɢɦ, ɱɬɨ ɮɭɧɤɰɢɹ
W
W
qpy
ɦɨɧɨɬɨɧɧɨ ɜɨɡɪɚɫɬɚɟɬ ɜ ɫɜɨɟɣ
ɨɛɥɚɫɬɢ ɨɩɪɟɞɟɥɟɧɢɹ (ɩɪɢ
0
z
W
) ɢ ɟɟ ɝɪɚɮɢɤ ɢɦɟɟɬ ɧɚɤɥɨɧɧɭɸ ɚɫɢɦɩɬɨɬɭ
W
p
y
ɢ ɜɟɪɬɢɤɚɥɶɧɭɸ ɚɫɢɦɩɬɨɬɭ 0
W
. Ʌɟɝɤɨ ɜɢɞɟɬɶ ɬɚɤɠɟ, ɱɬɨ ɭɪɚɜɧɟ-
ɧɢɟ (6.33) ɢɦɟɟɬ ɫɱɟɬɧɨɟ ɦɧɨɠɟɫɬɜɨ ɩɨɥɨɠɢɬɟɥɶɧɵɯ ɤɨɪɧɟɣ, ɹɜɥɹɸɳɢɯɫɹ
ɚɛɫɰɢɫɫɚɦɢ ɬɨɱɟɤ ɩɟɪɟɫɟɱɟɧɢɹ ɝɪɚɮɢɤɨɜ ɮɭɧɤɰɢɣ
l
y
W
ctg
ɢ
W
W
qpy
.
ɋɨɛɫɬɜɟɧɧɵɦ ɡɧɚɱɟɧɢɹɦ
2
nn
W
O
ɨɬɜɟɱɚɸɬ ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ
x
h
x)x(X
n
n
nn
W
W
W
sincos
1
, !,, 21
n .
ɂɫɩɨɥɶɡɭɹ ɮɨɪɦɭɥɵ (6.27) – (6.29), ɢɦɟɟɦ:
I
h
X
n
n
n
2
2
1
2
2
W
W
,
!,, 21
n
, (6.34)
ɝɞɟ
n
n
nn
n
)ȝlIJ(
l
I
P
WW
2
4
1
2
4
1
2
sinsin
, (6.35)
nn
h
W
P
1
ctg . (6.36)
ɂɡ (6.33) ɫɥɟɞɭɟɬ, ɱɬɨ
)hh(
hh
l
n
n
n
21
21
2
W
W
W
ctg , !,, 21
n . (6.37)
ȼɨɫɩɨɥɶɡɨɜɚɜɲɢɫɶ ɬɟɩɟɪɶ ɮɨɪɦɭɥɚɦɢ

36
D
D
D
2
ctg1
tgc
sin
2
2
,
ED
E
D
ctgctg
tgcctg
ctg
1
)ȕĮ(
,
ɫ ɭɱɟɬɨɦ (6.36), (6.37) ɧɚɯɨɞɢɦ, ɱɬɨ
n
nn
h
)l(
W
PW
2
ctg ,
2
2
2
2
2
2
h
h
)l(
n
n
nn
W
W
PW
sin ,
2
1
2
1
2
2
h
h
n
n
n
W
W
P
sin .
Ɉɬɫɸɞɚ ɢ ɢɡ (6.34), (6.35) ɫɥɟɞɭɟɬ, ɱɬɨ
)hIJ(
)hh()hhIJ()hIJ()hIJ(l
X
nn
nnn
n
2
2
22
2121
22
2
22
1
2
2
2
W
, !,, 21
n .
ɍɩɪɚɠɧɟɧɢɟ 4. ɂɫɩɨɥɶɡɭɹ ɩɪɢɦɟɪɵ 1 – 4, ɧɚɣɬɢ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟ-
ɧɢɹ, ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ ɢ ɤɜɚɞɪɚɬɵ ɧɨɪɦ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɜ ɡɚɞɚɱɟ
ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ ɫ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ II ɚ), III ɚ), III ɛ), IV ɛ), IV ɜ).
ȼ ɩɪɢɥɨɠɟɧɢɢ ɩɪɢɜɟɞɟɧɵ ɫɨɛɫɬɜɟɧɧɵɟ ɡɧɚɱɟɧɢɹ, ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤ-
ɰɢɢ ɢ ɤɜɚɞɪɚɬɵ ɧɨɪɦ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɞɥɹ ɜɫɟɯ ɬɢɩɨɜ ɝɪɚɧɢɱɧɵɯ ɭɫ-
ɥɨɜɢɣ I – IV.
§7. Ɋɟɲɟɧɢɟ ɫɦɟɲɚɧɧɵɯ ɡɚɞɚɱ ɞɥɹ ɭɪɚɜɧɟɧɢɹ
ɬɟɩɥɨɩɪɨɜɨɞɧɨɫɬɢ ɦɟɬɨɞɨɦ ɪɚɡɞɟɥɟɧɢɹ ɩɟɪɟɦɟɧɧɵɯ
1. ɋɦɟɲɚɧɧɚɹ ɡɚɞɚɱɚ ɞɥɹ ɨɞɧɨɪɨɞɧɨɝɨ ɭɪɚɜɧɟɧɢɹ ɬɟɩɥɨɩɪɨɜɨɞɧɨ-
ɫɬɢ ɫ ɨɞɧɨɪɨɞɧɵɦɢ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ.
Ɋɚɫɫɦɚɬɪɢɜɚɟɦɚɹ ɡɚɞɚɱɚ
ɮɨɪɦɭɥɢɪɭɟɬɫɹ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
Ɍɪɟɛɭɟɬɫɹ ɧɚɣɬɢ ɮɭɧɤɰɢɸ
)
t
x,(uu
, ɭɞɨɜɥɟɬɜɨɪɹɸɳɭɸ ɨɞɧɨɪɨɞ-
ɧɨɦɭ ɭɪɚɜɧɟɧɢɸ ɬɟɩɥɨɩɪɨɜɨɞɧɨɫɬɢ
xxt
uau
2
, l
x
0 , 0
!
t , (7.1)
ɧɚɱɚɥɶɧɨɦɭ ɭɫɥɨɜɢɸ
)
x(
)
x,(u
M
0
,
lx
d
d
0
(7.2)
ɢ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ
000
11
)t,(u)t,(u
x
E
D
, 0
!
t , (7.3)
0
22
)tl,(u)tl,(u
x
E
D
,
0
!
t
. (7.4)

37
Ɂɞɟɫɶ
0
!
a
,
0
!
l
,
1
D
,
1
E
,
2
D
,
2
E
– ɡɚɞɚɧɧɵɟ ɩɨɫɬɨɹɧɧɵɟ, ɩɪɢɱɟɦ
0
2
1
2
1
!
E
D
, 0
2
2
2
2
!
E
D
;
)
x(
M
– ɡɚɞɚɧɧɚɹ ɮɭɧɤɰɢɹ.
Ⱦɥɹ ɪɟɲɟɧɢɹ ɡɚɞɚɱɢ (7.1) – (7.4) ɪɚɫɫɦɨɬɪɢɦ ɫɥɟɞɭɸɳɭɸ ɜɫɩɨɦɨɝɚ-
ɬɟɥɶɧɭɸ ɡɚɞɚɱɭ:
ɇɚɣɬɢ ɧɟɬɪɢɜɢɚɥɶɧɵɟ ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ
xxt
UaU
2
,
lx
0
,
0
!
t
, (7.5)
ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɟ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ
000
11
)t,(U)t,(U
x
E
D
, 0
!
t , (7.6)
0
22
)tl,(U)tl,(U
x
E
D
,
0
!
t
(7.7)
ɢ ɩɪɟɞɫɬɚɜɢɦɵɟ ɜ ɜɢɞɟ
)
t
(
T
)
x(
X
)
t
x,U(
(7.8)
ɝɞɟ
)
x
(
X
– ɮɭɧɤɰɢɹ, ɧɟ ɡɚɜɢɫɹɳɚɹ ɨɬ ɩɟɪɟɦɟɧɧɨɣ t ,
)
t(
T
– ɮɭɧɤɰɢɹ, ɧɟ
ɡɚɜɢɫɹɳɚɹ ɨɬ ɩɟɪɟɦɟɧɧɨɣ x .
ɉɨɞɫɬɚɜɥɹɹ (7.8) ɜ (7.5) ɢ ɪɚɡɞɟɥɢɜ ɩɨɥɭɱɟɧɧɨɟ ɪɚɜɟɧɫɬɜɨ ɧɚ
)t(T)x(Xa
2
, ɢɦɟɟɦ:
)x(X
)x(X
)t(Ta
)t(T
c
c
c
2
. (7.9)
Ʌɟɜɚɹ ɱɚɫɬɶ ɪɚɜɟɧɫɬɜɚ (7.9) ɧɟ ɡɚɜɢɫɢɬ ɨɬ x , ɚ ɩɪɚɜɚɹ ɧɟ ɡɚɜɢɫɢɬ ɨɬ
t .
ɉɨɷɬɨɦɭ ɪɚɜɟɧɫɬɜɨ (7.9) ɜɨɡɦɨɠɧɨ ɥɢɲɶ ɜ ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ ɨɛɟ ɟɝɨ ɱɚɫɬɢ
ɪɚɜɧɵ ɩɨɫɬɨɹɧɧɨɣ:
const
c
c
c
O
)x(X
)x(X
)t(Ta
)t(T
2
(7.10)
(ɦɵ ɧɟ ɩɪɟɞɩɨɥɚɝɚɟɦ ɡɚɪɚɧɟɟ, ɤɚɤɨɣ ɡɧɚɤ ɢɦɟɟɬ ɩɨɫɬɨɹɧɧɚɹ
,
O
ɚɡɧɚɤ «– »
ɜ ɩɪɚɜɨɣ ɱɚɫɬɢ ɪɚɜɟɧɫɬɜɚ (7.10) ɢɫɩɨɥɶɡɨɜɚɧ ɞɥɹ ɭɞɨɛɫɬɜɚ ɩɨɫɥɟɞɭɸɳɟɝɨ
ɢɡɥɨɠɟɧɢɹ ɦɚɬɟɪɢɚɥɚ).
ɂɡ (7.10) ɩɨɥɭɱɚɟɦ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɵɟ ɭɪɚɜɧɟɧɢɹ ɨɬɧɨɫɢɬɟɥɶɧɨ
ɮɭɧɤɰɢɣ
)
t(
T
ɢ
)
x
(
X
:
0
2
c
)t(Ta)t(T
O
, (7.11)
0
cc
)
x
(
X
)
x
(
X
O
. (7.12)
ɉɨɞɫɬɚɜɥɹɹ (7.8) ɜ (7.6) ɢɜ (7.7), ɩɨɥɭɱɢɦ, ɱɬɨ ɮɭɧɤɰɢɹ
)
x(
X
ɞɨɥɠɧɚ
ɭɞɨɜɥɟɬɜɨɪɹɬɶ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ
000
11
c
)(X)(X
E
D
, (7.13)
38
0
22
c
)l(X)l(X
E
D
. (7.14)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɦɵ ɩɪɢɯɨɞɢɦ ɤ ɫɥɟɞɭɸɳɟɣ ɡɚɞɚɱɟ:
Ɍɪɟɛɭɟɬɫɹ ɧɚɣɬɢ ɜɫɟ ɡɧɚɱɟɧɢɹ ɱɢɫɥɨɜɨɝɨ ɩɚɪɚɦɟɬɪɚ
O
, ɩɪɢ ɤɨɬɨɪɵɯ
ɫɭɳɟɫɬɜɭɸɬ ɧɟɬɪɢɜɢɚɥɶɧɵɟ ɪɟɲɟɧɢɹ ɞɢɮɮɟɪɟɧɰɢɚɥɶɧɨɝɨ ɭɪɚɜɧɟɧɢɹ
(7.12), ɭɞɨɜɥɟɬɜɨɪɹɸɳɢɟ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ (7.13), (7.14), ɢ ɧɚɣɬɢ ɷɬɢ
ɪɟɲɟɧɢɹ. ɂɧɵɦɢ ɫɥɨɜɚɦɢ, ɦɵ ɩɪɢɯɨɞɢɦ ɤ ɪɚɫɫɦɨɬɪɟɧɧɨɣ ɜɵɲɟ ɡɚɞɚɱɟ
ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ ɨ ɧɚɯɨɠɞɟɧɢɢ ɫɨɛɫɬɜɟɧɧɵɯ ɡɧɚɱɟɧɢɣ ɢ ɫɨɛɫɬɜɟɧɧɵɯ
ɮɭɧɤɰɢɣ.
ȼ ɞɚɥɶɧɟɣɲɟɦ ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ ɝɪɚɧɢɱɧɵɟ ɭɫɥɨɜɢɹ (7.13),
(7.14) ɨɬɧɨɫɹɬɫɹ ɤ ɨɞɧɨɦɭ ɢɡ ɬɢɩɨɜ I – IV (ɫɦ. §6). Ɍɨɝɞɚ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɜɵ-
ɲɟ,
ɫɭɳɟɫɬɜɭɟɬ ɫɱɟɬɧɨɟ ɦɧɨɠɟɫɬɜɨ ɫɨɛɫɬɜɟɧɧɵɯ ɡɧɚɱɟɧɢɣ
0
t
n
O
,
!,, 21
n
, ɢ ɫɨɨɬɜɟɬɫɬɜɭɸɳɚɹ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ
^ `
)x(X
n
(ɫɦ. ɉɪɢɥɨɠɟɧɢɟ).
ɉɭɫɬɶ
)t(T
n
– ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (7.11) ɩɪɢ
n
O
O
:
0
2
c
)t(Ta)t(T
nnn
O
, !,, 21
n . (7.15)
Ɉɛɳɟɟ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (7.15) ɢɦɟɟɬ ɜɢɞ
)tȜa(A)t(T
nnn
2
exp
, (7.16)
ɝɞɟ
n
A – ɩɪɨɢɡɜɨɥɶɧɵɟ ɩɨɫɬɨɹɧɧɵɟ (ɜ ɞɚɥɶɧɟɣɲɟɦ ɦɵ ɫɱɢɬɚɟɦ ɢɯ ɨɬɥɢɱ-
ɧɵɦɢ ɨɬ ɧɭɥɹ, ɬɚɤ ɤɚɤ ɧɚɫ ɢɧɬɟɪɟɫɭɸɬ ɬɨɥɶɤɨ ɧɟɬɪɢɜɢɚɥɶɧɵɟ ɪɟɲɟɧɢɹ).
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɪɟɲɟɧɢɹɦɢ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɜɫɩɨɦɨɝɚɬɟɥɶɧɨɣ ɡɚɞɚɱɢ
(7.5) – (7.8) ɹɜɥɹɸɬɫɹ ɮɭɧɤɰɢɢ
)x(X)tȜa(A)t(T)x(X)tx,(U
nnnnnn
2
exp ,
!,, 21
n .
Ȼɭɞɟɦ ɢɫɤɚɬɶ ɪɟɲɟɧɢɟ ɢɫɯɨɞɧɨɣ ɡɚɞɚɱɢ ɜ ɜɢɞɟ ɪɹɞɚ, ɱɥɟɧɚɦɢ ɤɨɬɨɪɨɝɨ
ɹɜɥɹɸɬɫɹ ɮɭɧɤɰɢɢ
)tx,(U
n
:
¦¦
f
f
1
2
1 n
nnn
n
n
)x(X)tȜa(A)tx,(U)tx,(u exp
. (7.17)
ȿɫɥɢ ɪɹɞ (7.17) ɫɯɨɞɢɬɫɹ ɢ ɟɝɨ ɦɨɠɧɨ ɩɨɱɥɟɧɧɨ ɞɢɮɮɟɪɟɧɰɢɪɨɜɚɬɶ
ɞɜɚɠɞɵ ɩɨ
x
ɢɨɞɢɧɪɚɡɩɨ t , ɬɨ ɥɟɝɤɨ ɜɢɞɟɬɶ, ɱɬɨ ɟɝɨ ɫɭɦɦɚ
)
tx,(u
ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɭɪɚɜɧɟɧɢɸ (7.1) ɢ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ (7.3), (7.4). Ⱦɟɣɫɬ-
ɜɢɬɟɥɶɧɨ, ɢɡ ɩɨɫɬɪɨɟɧɢɹ ɮɭɧɤɰɢɣ
)tx,(U
n
ɫɥɟɞɭɟɬ, ɱɬɨ
> @
0
1
2
¦
f
n
nxxtnxxt
)tx,(U)tx,(U)tx,(ua)tx,(u
,

39
ɬɨ ɟɫɬɶ ɮɭɧɤɰɢɹ
)
tx,(u ɹɜɥɹɟɬɫɹ ɪɟɲɟɧɢɟɦ ɭɪɚɜɧɟɧɢɹ (7.1). Ⱥɧɚɥɨɝɢɱɧɨ
ɦɨɠɧɨ ɩɨɤɚɡɚɬɶ, ɱɬɨ ɞɚɧɧɚɹ ɮɭɧɤɰɢɹ ɭɞɨɜɥɟɬɜɨɪɹɟɬ ɭɫɥɨɜɢɹɦ (7.3), (7.4).
ȼɵɛɟɪɟɦ ɤɨɷɮɮɢɰɢɟɧɬɵ
n
A ɬɚɤ, ɱɬɨɛɵ ɮɭɧɤɰɢɹ
)
t
x,(u ɭɞɨɜɥɟɬɜɨ-
ɪɹɥɚ ɧɚɱɚɥɶɧɨɦɭ ɭɫɥɨɜɢɸ (7.2).
Ȼɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ ɮɭɧɤɰɢɹ
)
x(
M
ɦɨɠɟɬ ɛɵɬɶ ɪɚɡɥɨɠɟɧɚ ɜ ɪɹɞ
Ɏɭɪɶɟ ɩɨ ɫɢɫɬɟɦɟ ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɡɚɞɚɱɢ ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ:
¦
f
1n
nn
)x(X)x(
MM
, (7.18)
ɝɞɟ
xd)x(X)x(
X
n
l
n
n
³
0
2
1
MM
, !,, 21
n .
ɂɫɩɨɥɶɡɭɹ ɭɫɥɨɜɢɟ (7.2) ɢ ɪɚɜɟɧɫɬɜɚ (7.17), (7.18), ɢɦɟɟɦ:
¦¦
f
f
11
0
n
nn
n
nn
)x(X)x()x(XA)x,(u
MM
.
Ɉɬɫɸɞɚ ɫɥɟɞɭɟɬ, ɱɬɨ ɮɭɧɤɰɢɹ
)
tx,(u ɛɭɞɟɬ ɭɞɨɜɥɟɬɜɨɪɹɬɶ ɧɚɱɚɥɶɧɨ-
ɦɭ ɭɫɥɨɜɢɸ (7.2), ɟɫɥɢ
nn
A
M
,
!,, 21
n
.
ɂɬɚɤ, ɪɟɲɟɧɢɟ ɡɚɞɚɱɢ (7.1) – (7.4) ɢɦɟɟɬ ɜɢɞ
¦
f
1
2
n
nnn
)x(X)tȜa()tx,(u exp
M
. (7.19)
Ɋɚɫɫɦɨɬɪɟɧɧɵɣ ɦɟɬɨɞ ɪɟɲɟɧɢɹ ɡɚɞɚɱ ɦɚɬɟɦɚɬɢɱɟɫɤɨɣ ɮɢɡɢɤɢ, ɨɫɧɨ-
ɜɚɧɧɵɣ ɧɚ ɩɪɟɞɫɬɚɜɥɟɧɢɢ ɪɟɲɟɧɢɹ ɫɨɨɬɜɟɬɫɬɜɭɸɳɟɝɨ ɭɪɚɜɧɟɧɢɹ ɜ ɱɚɫɬɧɵɯ
ɩɪɨɢɡɜɨɞɧɵɯ ɜ ɜɢɞɟ ɩɪɨɢɡɜɟɞɟɧɢɹ ɮɭɧɤɰɢɣ, ɤɚɠɞɚɹ ɢɡ ɤɨɬɨɪɵɯ ɡɚɜɢɫɢɬ
ɬɨɥɶɤɨ ɨɬ ɨɞɧɨɣ ɩɟɪɟɦɟɧɧɨɣ (ɫɜɨɟɣ ɞɥɹ ɤɚɠɞɨɣ ɮɭɧɤɰɢɢ), ɧɨɫɢɬ ɧɚɡɜɚɧɢɟ
ɦɟɬɨɞɚ ɪɚɡɞɟɥɟɧɢɹ ɩɟɪɟɦɟɧɧɵɯ.
2. ɋɦɟɲɚɧɧɚɹ ɡɚɞɚɱɚ ɞɥɹ ɧɟɨɞɧɨɪɨɞɧɨɝɨ ɭɪɚɜɧɟɧɢɹ ɬɟɩɥɨɩɪɨɜɨɞ-
ɧɨɫɬɢ ɫ ɨɞɧɨɪɨɞɧɵɦɢ ɝɪɚɧɢɱɧɵɦɢ ɭɫɥɨɜɢɹɦɢ. ɍɤɚɡɚɧɧɚɹ ɡɚɞɚɱɚ ɮɨɪ-
ɦɭɥɢɪɭɟɬɫɹ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
Ɍɪɟɛɭɟɬɫɹ ɧɚɣɬɢ ɮɭɧɤɰɢɸ
)
t
x,(uu
, ɭɞɨɜɥɟɬɜɨɪɹɸɳɭɸ ɧɟɨɞɧɨ-
ɪɨɞɧɨɦɭ ɭɪɚɜɧɟɧɢɸ ɬɟɩɥɨɩɪɨɜɨɞɧɨɫɬɢ
)tx,(fuau
xxt
2
,
lx
0
, 0
!
t , (7.20)
ɧɚɱɚɥɶɧɨɦɭ ɭɫɥɨɜɢɸ
00
)
x,(u
,
lx
d
d
0
(7.21)

40
ɢ ɝɪɚɧɢɱɧɵɦ ɭɫɥɨɜɢɹɦ
000
11
)t,(u)t,(u
x
E
D
, 0
!
t , (7.22)
0
22
)tl,(u)tl,(u
x
E
D
, 0
!
t . (7.23)
Ɂɞɟɫɶ
)
tx,(
f
– ɡɚɞɚɧɧɚɹ ɮɭɧɤɰɢɹ, ɚ ɤɨɷɮɮɢɰɢɟɧɬɵ
2
a ,
1
D
,
1
E
,
2
D
,
2
E
ɭɞɨɜɥɟɬɜɨɪɹɸɬ ɬɟɦ ɠɟ ɭɫɥɨɜɢɹɦ, ɱɬɨ ɢ ɜ ɡɚɞɚɱɟ (7.1) – (7.4).
ȼ ɫɢɥɭ ɩɪɢɧɰɢɩɚ Ⱦɸɚɦɟɥɹ (ɫɦ. §5) ɪɟɲɟɧɢɟ ɡɚɞɚɱɢ (7.20) – (7.23)
ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ
³
t
d)IJIJ;tx,(v)tx,(u
0
W
, (7.24)
ɝɞɟ
)
IJt;x,(
v
v
– ɪɟɲɟɧɢɟ ɡɚɞɚɱɢ
xxt
vav
2
, lx
0 , 0
!
t
, (7.25)
)
IJ
x,(
f
)
IJ
;x,(v
0 , l
x
d
d
0 , (7.26)
000
11
);t,(v);t,(v
x
W
E
W
D
, 0
!
t , (7.27)
0
22
)t;l,(v)t;l,(v
x
W
E
W
D
, 0
!
t
. (7.28)
ȼ ɞɚɥɶɧɟɣɲɟɦ ɛɭɞɟɦ ɩɪɟɞɩɨɥɚɝɚɬɶ, ɱɬɨ ɩɪɢ ɤɚɠɞɨɦ ɮɢɤɫɢɪɨɜɚɧɧɨɦ
0
!
W
ɮɭɧɤɰɢɹ
)
,x(
f
W
ɦɨɠɟɬ ɛɵɬɶ ɪɚɡɥɨɠɟɧɚ ɜ ɪɹɞ Ɏɭɪɶɟ ɩɨ ɫɢɫɬɟɦɟ
ɫɨɛɫɬɜɟɧɧɵɯ ɮɭɧɤɰɢɣ ɡɚɞɚɱɢ ɒɬɭɪɦɚ-Ʌɢɭɜɢɥɥɹ:
¦
f
1n
nn
)x(X)IJ(f)x,(f
W
,
ɝɞɟ
xd)x(X)x,(f
X
)IJ(f
n
l
n
n
³
0
2
1
W
, !,, 21
n .
Ɍɨɝɞɚ, ɤɚɤ ɩɨɤɚɡɚɧɨ ɜɵɲɟ, ɡɚɞɚɱɚ (7.25) – (7.28) ɢɦɟɟɬ ɪɟɲɟɧɢɟ
¦
f
1
2
n
nnn
)x(X)tȜa()IJ(f);tx,(v exp
W
. (7.29)
ɉɨɞɫɬɚɜɥɹɹ (7.29) ɜ (7.24) ɢ ɢɡɦɟɧɹɹ ɦɟɫɬɚɦɢ ɫɭɦɦɢɪɨɜɚɧɢɟ ɢ ɢɧɬɟɝ-
ɪɢɪɨɜɚɧɢɟ, ɧɚɯɨɞɢɦ, ɱɬɨ
¦
f
1n
nn
)x(X)t(T)tx,(u ,
ɝɞɟ
