Kristiansen Svein. Maritime Transportation: Safety Management and Risk Analysis
Подождите немного. Документ загружается.


The probability of an impact accident can on the basis of this model be expressed by
the product of two probabilities that reflect the transitions from normal operation state
(opportunity) to the accident state:
PðAÞ¼PðCÞPðI
j
CÞð6:2Þ
where:
P(A) ¼ Probability of an impact accident per passage
P(C) ¼ Probability of losing vessel control per passage
P(I|C) ¼ Conditional probability of having an accident given loss of vessel control
(incident)
The probability of losing control, P(A), is assumed to have a constant value that is
independent of time and reflects the overal l operational standard of the vessel or group of
vessels. The conditional probability of having an impact accident after losing control is
in reality a function of the vessel’s ability to handle emergencies. Rather than trying
to estimate this directly, one may either compute the number of accidents relative to the
number of incidents, or assess the probability on the basis of the traffic or fairway
condition. It is fairly evident that the risk of an accident is greater the more dense the traffic
or narrow a fairway. In the following sections, different approaches will be shown for
estimating the conditional probability of having an impact accident P(I|C).
The equation will for convenience be written as follows:
P
a
¼ P
c
P
i
ð6:3Þ
where the indexes denote accident (a), loss of control (c) and impact (i).
6.4 GRO U N DING AND STRAN DING MODELS
A ship moving in a restricted seaway without any other traffic is subject to stranding and
grounding hazards. The coastal zones, shoals, rocks and islands are basically stationary
objects relative to the vessel. The estimation of the probability that an incident will lead to
an accident will be based on certain assumptions of how the vessel moves in the critical
phase. As the first step we will model this aspect and subsequently look at the probability
of losing vessel control.
Figur e 6.2. Conceptual impact accident model.
13 6 CHAPTER 6 TRAFFIC-BASED MODELS

6.4.1 Grounding
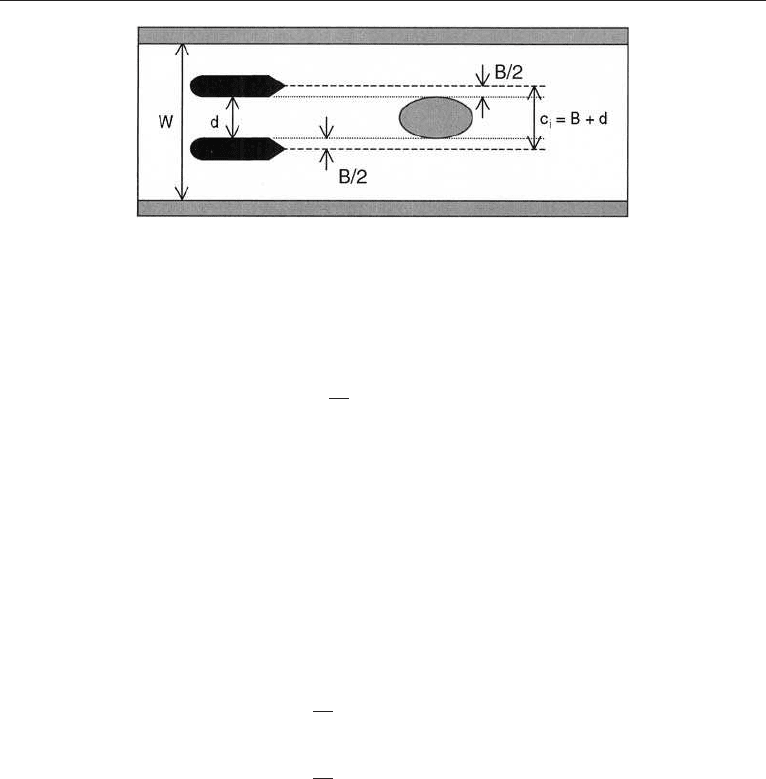
The grounding scenario is based on a straight fairway section as shown in Figure 6.3.
Assume that control of a ship is lost owing to failure in the navigation system due to
either technical or human factors or both. The ship’s lateral position within the fairway
width is assumed to be random at the time when control is lost. The distance of the fairway
section is denoted D, and let us further assume that the vessel is positioned randomly
anywhere along this track (longitudinally). In the critical (incident) phase it is a
simplification, assuming that the vessel continues on an unchanged straight course. The
situation is shown in Figure 6.3.
The probability that the uncontrolled vessel hits the obstacle is then exclusively
dependent on the dimensions of the fairway and the beam of the ship:
P
i
¼
B þ d
W
ð6:4Þ
where:
W ¼ Average width of fairway
d ¼ Cross-section of obstacle, e.g. shoal, rock, island, etc.
B ¼ Breadth of vessel
This fairly simple model is based on the assumption that the vessel may have any
transverse position in the seaway and that the breadth of the critical corridor is given by
the term c
i
¼B þd as indicated in Figure 6.4. The probability is thereby given by the
ratio between these two terms.
In a seaway with a number of obstacles the conditional probability of an impact is
given by the union of the cross-section of the obstacles:
P
i
¼
1
W
B þ d
1
[
d
2
[
...
[
d
k
hi
Figure 6.3. Modell ing of a grounding accident.
6.4 GR OUNDING AND STRANDING MODELS 137
or simply by assuming no overlap between the obstacles:
P
i
¼
1
W
B þ
X
k
d
k
"#
ð6:5Þ
In a fairway with numerous shoals and other hindrances the number of such obstacles may
also be expressed in the following manner:
K ¼ D W
where ¼obstacle density (obstacles/area-unit).
By replacing the sum expression in Eq. (6.5) with the number of obstacles, the
following expression is obtained:
P
i
¼
1
W
ðB þ D W dÞ
¼
B
W
þ D d
If the ship’s beam is considered small relative to the fairway width, we get:
P
i
¼ D d ð6:6Þ
A final comment should be made on how this model may be enhanced in order to
improve its validity. Instead of using the physical barriers of a fairway to specify potential
lateral positions of the ship, a lane may be defined that more realistically describes the
actual maritime traffic (see Figure 6.5). It is also a fact that the traffic density is decreasing
as one approach es the shore. A more realistic model would therefore be to apply a traffic
distribution model to reflect this.
Figur e 6.4. Characteristic parameters of the grounding situation.
13 8 CHAPTER 6 TRAFFIC-BASED MODELS
Case Study
Problem
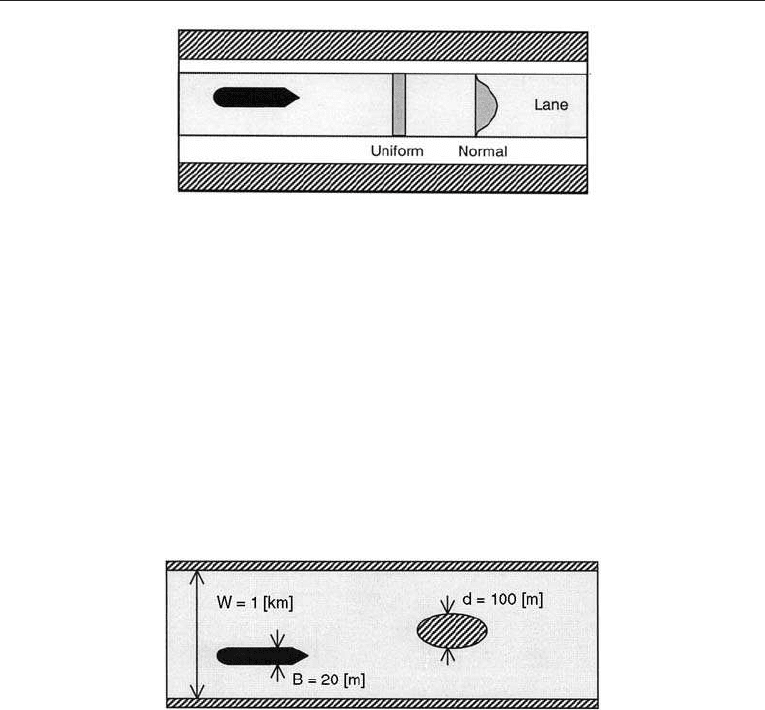
A new oil refinery is under planning. Oil is going to be transported to and from the
terminal by tankers through a fjord of width 1 km. There is an island in the middle of the
fairway representing a grounding hazard. The width of the island is equal to 100 meters.
The planned capacity of the oil refinery requires 6 shipments for export and 3 shipments
for import daily. The mean beam of these ships is 20 metres. The risk of grounding has to
be quantified in order to compare the risk of oil spill for this and eventually other locations
of the refinery.
Solution
Estimate the expected number of groundings on the island per year.
Assumptions:
The probability of losing navigational control P
c
is equal to 1.4 10
4
per passage of
the fairway. The ship’s lateral position within the width of the fairway is uniformly
distributed. Import ing and exporting vessels are respectively leaving and entering the port
in ballast condition.
Analysis
The number of ships passing the fairway each year is:
N
p
¼ 2 ð6 þ 3Þðpassages=dayÞ365 ðdays=yearÞ¼6570 ðpassages=yearÞ
Figure 6.5. Enhanced groun ding scenari o.
6.4 GR OUNDING AND STRANDING MODELS 139

The impact diameter is:
d
i
¼ 20 ðmÞþ100 ðmÞ¼120 ðmÞ
The conditional probability of grounding after loss of navigational control is:
P
i
¼
d
i
W
¼
120 ðmÞ
1000 ðmÞ
¼ 0:120
The probability of grounding per passage of the fairway is:
P
a
¼ P
c
P
i
¼ 1:4 10
4
0:120 ¼ 1:68 10
5
Based on the assumptions and the given pro bability data, a grounding on the island within
one year is equal to 1.68 10
5
. The average time between groundings is given by the
reciprocal value:
T ¼ 10
5
=1:68 ¼ 59,524 years
In other words , not a very likely event.
Comment
The probability of other impact accidents such as strandings and collisions should also
be estimated in order to assess the total risk of impact accidents for this fairway. The
total accident frequency should be compared for alternative locations. The conditional
probability of an oil spill given an impact accident must also be estimated in order to
have the complete risk picture. W hether grounding leads to an oil spill is dependent on
a number of factors such as ship speed, cargo containment system (hull design) and
weather conditions.
6.4.2 Stranding
Recalling the straight line fairway scenario in the previous section, there is also a risk of
stranding. The term stranding is used for the impact with the shoreline in contrast to the
impact with individual shoals and islands in the fairway. A random position for the vessel
in the seaway is again assumed and as an average value the centre location as shown in
Figure 6.6.
The model will be based on the assumption that in the case of loss of control the vessel
may continue on any course ahead, e.g. a course within a span of 180
. As can be seen from
the figure, the critical angle leading to stranding at both sides is equal to . It is fair to
assume that the length of the fairway D is considerably greater than the width W, or:
W
D
2
< 1
14 0 CHAPTER 6 TRAFFIC-BASED MODELS

The conditional probability of stranding is given by the ratio of the critical angle to the
total angle (expressed for one lateral side):
P
i
¼
=2
¼
arctanð D=2ðÞ=ðW=2ÞÞ
=2
By replacing the arctan term by the following series expansion, we get:
P
i
¼
=2 þ
P
n
ð1Þ
n
W=DðÞ
2n1
=ð2n 1Þ
=2
¼
2
2
W
D
þ
W
D
2
W
D
3
...
"#
The two first co mponents in the series may be used as an approximation for the whole
series expression. The equation then takes the following simplified form:
P
i
1
2
W
D
ð6:7Þ
6.4.3 A Comme n t on t he Stranding Mod e l
The estimates from the model rest to a large degree on the relative distance of the fairway
section that is studied. Let us take a fairway 10 nm long and of width 0.5 nm. The
conditional stranding probability is:
P
i
1
2
0:5
10
¼ 0:032 3%
On the other hand one may assume that the maximum time that the vessel will
continue without control is 10 minutes. With a speed of 15 knots, this corresponds to a
distance of 2.5 nm. It would therefore seem more correct to model two sections, each of a
distance of 5 nm. The average distance sailed within a section of 5 nm is one half or 2.5 nm.
Figure 6.6. Stranding model.
6.4 GR OUNDING AND STRANDING MODELS 141

The estimate of the probability of stranding in the first secti on but not stranding in the
other section is:
P
1
¼ 1
2
0:5
5
¼ 0:064 6%
P
2
¼ 1 P
1
¼ 0:936
P
12
¼ P
1
P
2
¼ 0:064 0:936 ¼ 0:060 ¼ 6%
This confirms that the assumption about average time to regain vessel control and
thereby selection of fairway section distance has a vital impact on the estimated
probability. On the other hand, it should not be forgotten that these models are used
primarily for comparing alternatives and that less weight is put on the absolute numbers.
6.5 LOSS OF NAVIGATIONAL CONTROL
In order to calculate the probability of having an impact accident within a fairway, the
probability of losing navigational control P
c
has to be quantified also. It might be the case
that the value of P
c
is different for stranding and grounding situations as they represent
different navigation tasks. Hence, the value of P
c
for stranding and grounding situations
should be estimated separately. We have the following general expression based on Eq. (6.3):
P
c
¼
P
a
P
i
ð6:8Þ
The probability of loss of control P
c
can be estimated on the basis of observation of traffic,
counting of accidents and estimating the geometric probability P
i
for a specific fair way. In
the following sections it will be shown how this was done in some pioneering studies for
Japanese coastal waters.
6.5.1 JapaneseTraffic Studies (Fujii,1982)
Uraga Strait
The Uraga Strait, which is located at the entrance to Tokyo Bay, has several obstacles
which make it necessary for any passing ship to change course several times in order to
avoid stranding. Roughly estimated, the conditional probability of stranding in case of
loss of control could be set to be P
i
¼1.0.
The num ber of accidents for ships greater than 300 GRT had been counted for the
period from 1966 to 1970 and was in total N
a
¼16. The corresponding number of ship
passages (or movements) in the same period was N
m
= 140,000. The loss of control
probability can then be estimated for this fairway:
P
a
¼
N
a
N
m
¼
16
140,000
¼ 1:1 10
4
P
c
¼
P
a
P
i
¼
1:1 10
4
1:0
¼ 1:1 10
4
142 CHAPTER 6 TRAFFIC-BASED MODELS

The probability of losing navigational control per passage of the Uraga Strait may
therefore be set to be 1.1 10
4
.
An interesting fact was that 15 of the ships involv ed in accidents were sailing under
a foreign flag. However, the foreign flag vessels represented only 50% of the traffic
through the fairway. Consequently there was a significantly higher accident risk for
foreign vessels compared with Japanese.
The Bisanseto fairway
Ozeishima Island is located in a curved part of the Bisanseto fairway. The probability of
impact, given loss of navigational control, P
i
, for the fairway was estimated to be 0.25 on
the basis of the topological characteristics (Table 6.2). Based on Eq. (6.8), the probability
of loss of navigational control for different vessel size categories was estimated in the same
manner as for the Uraga Strait.
Naruto Strait
Zakace is the headland in the narrowest part of the Naruto Strait. The hindrance due
to Zaka ce constitutes one-fifth of the fair way width. The geometrical probability of an
impact is therefore estimated to be 0.20. The traffi c flow and the number of impact
accidents are presented in Table 6.3.
Akashi Strait
During the construction work on a bridge over the 4 km wide Akashi Strait, a platform
was pos itioned in the middle of the fairway. There were several ship impac ts with the
platform during the 70-month construction period. The impact diameter of the platform
was 0.2 km. The geometrical probability is calculated according to Eq. (6.4):
P
i
¼
0:2
4:0
¼ 0:05
Ta b l e 6 . 2 . Characteristics of the Bisanseto fairway g rounding accidents
Tonnage (GRT) N
a
N
m
P
a
P
i
P
c
<100 21 300,000 0.7 10
4
0.25 2.8 10
4
100–500 15 180,000 0.8 10
4
0.25 3.3 10
4
<500 6 120,000 0.5 10
4
0.25 2.0 10
–4
Table 6.3. Characteristics of the Naruto Strait grounding accidents
N
a
N
m
P
a
P
i
P
c
11 730,000 0.2 10
4
0.20 0.8 10
4
6. 5 LO S S OF NAVIGAT IONAL CONTROL 143

Table 6.4 summarizes the Akashi Strait study findings. The resulting probability of loss
of vessel control was estimated to be 1 10
4
.
Summary of the Japanese investigations
The investigations presented above show that the probability of losing navigational
control varies from 0.8 10
4
to 3.3 10
4
. Based on these investigations, the following
mean value is proposed:
P
c
¼ 2:0 10
4
ð1=passageÞ
In certain risk assessment studies it might be necessary to take the effect of sailing
distance into consideration. Assuming that the average distance of the critical part of the
fairway in the previous studies can be set to 10 nm, the loss of control frequency can be
computed as:
c
¼ P
c
=D ¼ 2:0 10
5
ð1=nmÞ
6.5.2 Alternative Estimates
In order to qualify the results of the Japanese studies, an alte rnative approach might
be tried. The failure frequency of the steering system was estimated in an American
investigation (Ewing, 1975) as:
ss
¼ 0:41 ðfailures=yearÞ
Assuming 48% of the time at sea, we have 175 sailing days each year and the following
hourly frequency:
ss
¼ 0:41=ð175 24Þ¼1 10
4
ðfailures=hourÞ
The relative distribution of factors of causes leading to grounding accidents
for Norwegian ships greater than 1599 GRT is shown in Tabl e 6.5 (Kristiansen and
Karlsen, 1980). On the basis of this investigation it could be concluded that 1/50 of the
Ta b l e 6 . 4 . Characteristics of the Akashi Strait impact accidents
N
a
N
m
P
a
P
i
P
c
16 2,430,900 0.07 10
4
0.05 1.4 10
4
14 4 CHAPTER 6 TRAFFIC-BASED MODELS

accidents were caused by failure of the steering machine. Hence, the total failure rate can
be estimated to be:
¼ 50 1 10
4
¼ 5 10
3
ðfailures=hourÞ
The American study further estimated that only 5% of the failures led to an impact
accident. By assuming that the mean sailing speed is equal to 10 knots, the following
estimate of the accident frequency can be made:
c
¼ 0:05 5 10
3
=10 ¼ 2:5 10
5
ðfailures=nmÞ
Ta b l e 6 . 5 . Distribution of primary causal factors in grounding accidents for Norwegian ships greater than
1599 GRT,1970 ^78
Causal factor group Causal factor Frequency
abs. %
I. External factors G. External conditions influencing navigation
and auxiliary equipment
8 1.9
I. Less than adequate markers and buoys 27 6.4
P. Reduced visibility 53 12.6
Q. External influences like channel and shallow
water effect.
79 18.9
II. Technical failure A. Failure in ship’s technical systems 24 5.7
C. Serviceability of navigational aids 8 1.9
D. Remote control of steering and propulsion 3 0.7
F. Failure in communication equipment 2 0.5
III. Navigation factors B. Bridge design and arrangement 1 0.2
F. Error/deficiency in charts or publications 34 8.1
M. Bridge manning and organization 35 8.4
O. Internal communicational failure 5 1.2
X. Inadequate knowledge and experience 4 1.0
IV. Navigation error R. Failure due to navigation and manoeuvring 49 11.7
T. Wrong use of the information from
buoys and markers
35 8.4
S. Failure in operation of equipment 10 2.4
U. Wrong appreciation of traffic information 2 0.5
V. Non-compliance N. Inadequate coverage of watch 24 5.7
V. Special human factors 10 2.4
VI. Other ships H. Fault or deficiency of other ship — —
Y. Navigational error on other ship 6 1.4
Sum 419
Source: Kristiansen and Karlsen (1980).
6. 5 LO S S OF NAVIGAT IONAL CONTROL 14 5
