Kristiansen Svein. Maritime Transportation: Safety Management and Risk Analysis
Подождите немного. Документ загружается.


100 weeks. Table 5.2 shows that the number of accidents per week has varied between
0 and 3 with dominance on the lower values. The mean number was 0.9 accidents per
week. This indicates that the Poisson distribution might be appropriate to describe the
frequency of LTA.
In order to test the feasibility of the Poisson distribution we will compare
what this model would give with observed values. Table 5.3 summarizes the
computations.
The first step is to compute the PDF for ¼0.9. Statistical experience says that any
value should not be lower than 0.05, and this requires that the distribution is truncated
by grouping the values from X ¼3 to 6 together, which adds up to 0.0628 (see the
shaded area in the table).
The next step is to compute the estimated number of weeks on the basis of a 100 weeks
observation period.
Ta b l e 5 . 2 . Number of lost-time accidents per week
LTA/Week
X
Observed weeks
N
X N
045 0
129 29
217 34
3927
4
5
6
Sum: 100 90
Mean: 0.9
Table 5.3. Testing of the Poisson distribution: sum of squared deviations
LTA/week Poisson PDF Poisson PDF Expected Observed (O E)
2
/E
X corrected weeks weeks
0 0.4066 0.4066 40.66 45 0.4639
1 0.3659 0.3659 36.59 29 1.5749
2 0.1647 0.1647 16.47 17 0.0173
3 0.0494 0.0628 6.28 9 1.1767
4 0.0111
5 0.0020 Sum: 3.2328
6 0.0003
Part sum 0.0628
126 CHAPTER 5 DECISIONS IN OPERATION

It can now be proved that the sum of the relative difference between number of
observed weeks (O) and estimated weeks (E) is chi-square distributed:
2
calc
¼
X
N
O EðÞ
2
E
The distribution applies for positive values and has the parameter , which denotes the
number of degrees of freedom and is given by:
¼ðN 1Þ1
where N is the number of observations and the second 1 is the consequence of
introducing an estimate for in the computations.
If our hypothesis that the number of weeks is given by the Poisson distribution
is true (H
0
), the calculated value of the chi-square criterion should be less than
the critical value. We are then able to test the assumption of a Poisson distribution as
follows:
from Table 5.3:
2
calc
¼ 3:2328
degrees of freedom: ¼(4 1) – 1 ¼2
assuming significance level: ¼0.95
tabulated value (from handbook):
2
2,0:95
¼ 5:99
It can be concluded that the Poisson distribution is valid as the calculated value (3.23) is
less than the tabulated value.
5. 5 CHOOSING AMONG ALTERNATIVE TR AINING PROGR AMS
The chi-square test can also be useful for testing other models. Let us take the following
case described by ReVelle and Stephenson (1995). A company has tried out training
programmes of different duration: 1, 3, 5 and 10 days. The attending crew member s were
subject to a rating by their supervisors 6 months after the training session. The supervisor
used the follo wing ranking: excellent, good or poor.
The result of the assessment is shown in the upper part of Table 5.4. Observation of
the data may support the suspicion that there is no clear relationship between course
duration and rating. It is interesting to note the low number of ‘excellent’ ratings for the
participants in the 10-day program.
Against this background, it may be interesting to test the following null-hypothesis:
H
0
¼ No correlation between Duration and Rating
5.5 CHOOSING AMONG ALTERNATIVE TRAINING PR OG RAMS 127

Given this hypothesis, the distribution of the number of crew members would follow this
computational rule:
Cell Row
i
, Column
j
¼
SumðRow
i
ÞSumðColumn
j
Þ
SumðRows & ColumnsÞ
which expresses the a ssumption of independence by the fact that the number in each cell is
only determined by the column and row sums. Applying this rule to each cell in the table,
we get the expected result shown in the middle part of Table 5.4.
Based on the upper and middle parts of the table, we are now in a position to calculate
the chi-square value as outlined in the previous chapter:
2
calc
¼
X
N
O EðÞ
2
E
The result of for each cell is shown in the lower part of Table 5.4 and the sum is:
2
calc
¼ 10:8736
Ta b l e 5 . 4 . Analysis of training effectiveness
Excellent Good Poor Sum
(a) Observed rating
1 day 6 12 0 18
3 days 12 25 6 43
5 days 14 31 12 57
10 days 2 23 7 32
Sum 34 91 25 150
(b) Estimated rating
1 day 4.08 10.92 3 18
3 days 9.75 26.09 7.17 43
5 days 12.92 34.58 9.50 57
10 days 7.25 19.41 5.33 32
Sum 34 91 25 150
(c) Relatively squared difference
1 day 0.9035 0.1068 3.0000 4.0103
3 days 0.5209 0.0453 0.1899 0.7561
5 days 0.0903 0.3706 0.6579 1.1188
10 days 3.8048 0.6626 0.5208 4.9883
10.8736
128 CHAPTER 5 DECISIONS IN OPERATION

The number of degrees of freedom is given by following formula:
¼ (Number of rows 1Þ(Number of columns 1Þ
¼ð4 1Þð3 1Þ
¼ 6
Assuming a significance level ¼0.99, we find the following tabulated value:
2
6,0:99
¼ 16:8.
It can be concluded that the ‘no relationship’ hypothesis holds as the calculated value is
less than the tabulated value. This means that the variation in ratings is not more than
would be expected under the null-hypothesis H
0
. Or in other words, it is not possible to
explain the variation in rating by the course duration.
It should, however, be pointed out that this conclusion is based on a very high
value for the significance level: ¼0.99. This reflects our concern of not rejecting a true
H
0
. If we decided to be more open to the alternative hypothesis that there is a relation-
ship between course duration and rating, we might have set the significance level
somewhat lower:
¼ 0:95
2
6,0:95
¼ 12:6
This result did not, howeve r, change our conclusion as the tabulated value still is higher
than the one calculated.
5.5 CHOOSING AMONG ALTERNATIVE TRAINING PR OG RAMS 129

REFEREN CES
Aitken, J. D. et al., 1996, Committed HSE management vs. TQM: Is there any difference?
International Conference on Health, Safety and Environment, Paper SPE 35760, 9–12 June, New
Orleans, Louisiana.
ReVelle, J. B. and Stephenson, J., 1995, Safety Training Methods: Practical Solutions for the Next
Millennium. John Wiley, New York.
Wills, T. L. et al., 1996, The use of integrated management systems assessments for continous
improvement of EHS programs. International Conference on Health, Safety and Environment,
Paper SPE 35887, 9–12 June, New Orleans, Louisiana.
13 0
PART III
RISK ANALYSIS

6
TR AFFIC -BASED MODELS
Shipwreching on land is worse than at sea — the sea at least has a strand.
(Johan Falkberget, Norwegian author)
6.1 INTRODUCTION
Earlier, it ha s been shown how to estimate the probability of an accident based on
historical accident numbers. The simplest and most intuitively correct manner is to base
accident frequency estimates on exposure criteria such as vessel-years (i.e. number of
vessels at risk per year). However, such a statistical approach may only describe the mean
risk of a large number of ships and not reflect variation in technical standards,
environmental conditions and traffic density. In certain instances the analysis of risk will
be undertaken for specific fleets or for certain waters or fairways. This demands another
method than the statistical approach based on fleet-year exposure. In this chapter it will be
shown how the probability of an impact-type accident can be estimated for a specified
seaway. By an impact-type accident we mean collision, grounding, stranding or allision
(above-water obje ct impact).
6.2 BASIC THEORY
It has earlier been shown that the expected number of ship accidents per unit of time in a
specified fairway may be estimated by the following equation:
C ¼ N
where:
C ¼ Expected number of accidents in seaway per time-unit
¼ Number of accidents per vessel-passage of seaway
N ¼ Number of passage s per time unit
A voyage may for computational reasons be defined as the passing of a sequence
of fairway sections. As a simplification, it is further assumed that the navigational and
topological characteristics are relatively constant within each section of the fairway.
133

Consequently, the traffic density and other environmental conditions can be assumed to
be relatively unchanged within each section. Previously it was shown that phenomena with
a small chance of occurring have an expected frequency (events per unit of time) that is
equal to the probability of realization. This assumption holds, for instance, for the Poisson
model. The expected number of impact accidents within the mth fairway section can then
be expressed as follows:
C
m
¼
m
N ¼ PðCÞ
m
N
where:
C
m
¼ Expe cted number of impact accidents per time-unit within the mth fairway
section
P(C)
m
¼ Probability of impact accident when passing the mth fairway section
By referring to the potential accident type with index u, the expected number of
accidents of type u within section m of the fairway may be expressed as:
C
m,u
¼
m,u
N ¼ PðCÞ
m,u
N
Hence the estimated total number of accidents per time-unit for the whole voy age, C
T
,
may be expressed as follows:
C
T
¼
X
m
X
u
m,u
N
m
¼
X
m
X
u
PðCÞ
m,u
N
m
ð6:1Þ
where:
P(C)
m,u
¼ Probability of impact accident type u per passage of fairway section m
N
m
¼ Number of passing ships per time unit
The expected accident frequency is in other words calculated by summing over all
fairway sections and all accident types. How the fairway is split up into sections will to a
certain degree be a subjective matter, but should as already mentioned take the traffic and
topography into consideration. It will obviously be a compromise between computational
efficiency and a need for homogeneous conditions within each section. A very simplified
fairway representation is shown in Figure 6.1 and consists of the following three sections:
A. Fairw ay with traffic in the same and head-on direction.
B. Cros sing traffic in each direction.
C. Fairway with an obstacle (shoal) and traffic in both the same and the head-on
directions.
134 CHAPTER 6 TRAFFIC-BASED MODELS
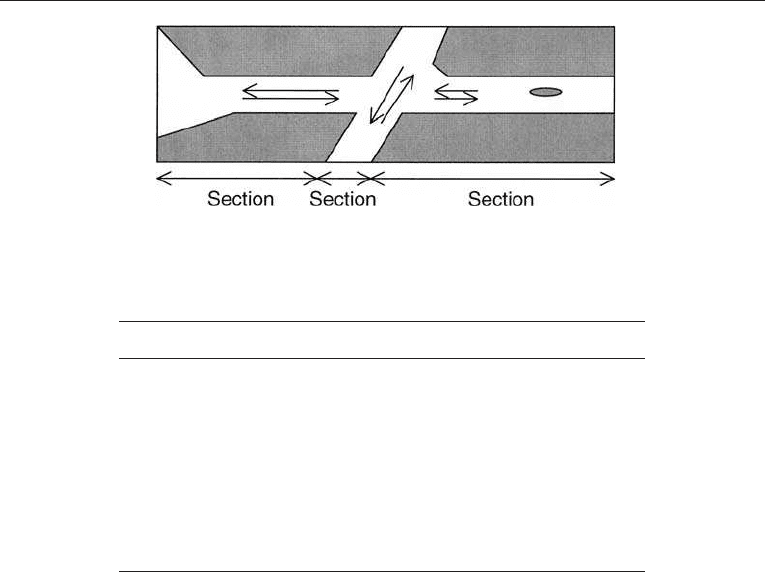
This generates a total of eight different accident situati ons as shown in Table 6.1. The
different impact accidents will now be treated in detail in the following sections. Modelling
of each accident type will require different ap proaches.
6. 3 A GENER AL MODEL OF IMPACT ACCIDENTS
The models that will be proposed for estimation of impact accident frequency are all based
on following premises:
1. The vessel has an opportunity to be put at risk.
2. The vessel will be subject to an incident that puts it at risk.
3. The vessel is unable to handle the incident and will thereby have an accident.
The first requirement means that the vessel is underway or sailing. The second
requirement is that for some unspecified reason the vessel has lost control and thereby is
subject to an incident. Thirdly, the incident may lead to an accident in the case where the
situation is not corrected in due time (see Figure 6.2). The most relevant parameter for the
first condition is the duration of the operation or voyage. The second condition can be
expressed by a probability of having an incident, whereas the third condition is given by a
conditional probability of having an accident given to be in an incident situation.
Figure 6.1. Selection of sections for a general traffic fairway.
Ta b l e 6 . 1 . P ot e nt ia l accid e nt situat i ons
Section Potential accident situations
A 1. Collision with ships on the same course
2. Head-on collision
3. Stranding
B 4. Collision with crossing traffic
C 5. Collision with ships on the same course
6. Head-on collision
7. Stranding
8. Grounding on shoal in fairway
6.3 A GEN ERAL MO DEL OF IM PA CT AC CI DENTS 135
