Крамаренко А.А., Широких Л.А. Лекции по строительной механике стержневых систем. Часть 3: Статически неопределимые системы. Метод сил
Подождите немного. Документ загружается.

97 98
3. Смирнов А.Ф. Строительная механика. Стержневые системы:
Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащени-
ков, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.
Гл. XI. Метод сил. § 59. Канонические уравнения и их особенно-
сти. § 60. Общий алгоритм расчёта. – С. 316–332. § 64. Расчёт ста-
тически неопределимых систем в матричной форме. – С. 368–381.
4.
Клейн Г.К. Руководство к практическим занятиям по курсу строи-
тельной механики. Статика стержневых систем: Учеб. пособие /
Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.
Гл. IX. Расчёт рам методом сил. § IX.1. Порядок расчёта рам. –
С. 137–145. § IX.7. Расчёт рам в матричной форме. – С. 169–181.
5. Анохин Н.Н. Строительная механика в примерах и
задачах.
Ч. 2. Статически неопределимые системы: Учеб. пособие /
Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 2000. –
464 с.
Гл. 5. Расчёт сооружений методом сил. § 5.1. Основная идея метода
сил. Выбор рациональной основной системы. Примеры 5.1–5.5. –
С. 8–15. § 5.2. Силовое воздействие. Примеры 5.12–5.13. – С. 23–
35.
6. Проценко В.М. Расчёт статически неопределимых рам: Методиче-
ские указания / В.М.
Проценко, В.Г. Себешев. – Новосибирск:
НГАС, 1993. – 56 с.
Задача № 1. Расчёт плоской статически неопределимой рамы мето-
дом сил. – С. 1–28.

97 98
ЛЕКЦИЯ СЕМНАДЦАТАЯ
РАСЧЁ Т СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
МЕТОДОМ СИЛ НА ТЕМПЕРАТУРНОЕ
И КИНЕМАТИЧЕСКОЕ ВОЗДЕЙСТВИЕ
17.1. Расчёт стержневых статически неопределимых
систем на температурное воздействие
17.2. Пример расчёта статически неопределимой ра-
мы на температурное воздействие в обычной
форме
17.3. Пример расчёта статически неопределимой ра-
мы на температурное воздействие в матричной
форме
17.4. Расчёт стержневых статически
неопределимых
систем на кинематическое воздействие
17.5. Пример расчёта статически неопределимой ра-
мы на смещение опорных связей в обычной
форме
17.6. Пример расчёта статически неопределимой ра-
мы на смещение опорных связей в матричной
форме
17.7. Вопросы для самопроверки
17.8. Рекомендуемая литература
17.1. Расчёт стержневых статически неопределимых
систем на температурное воздействие
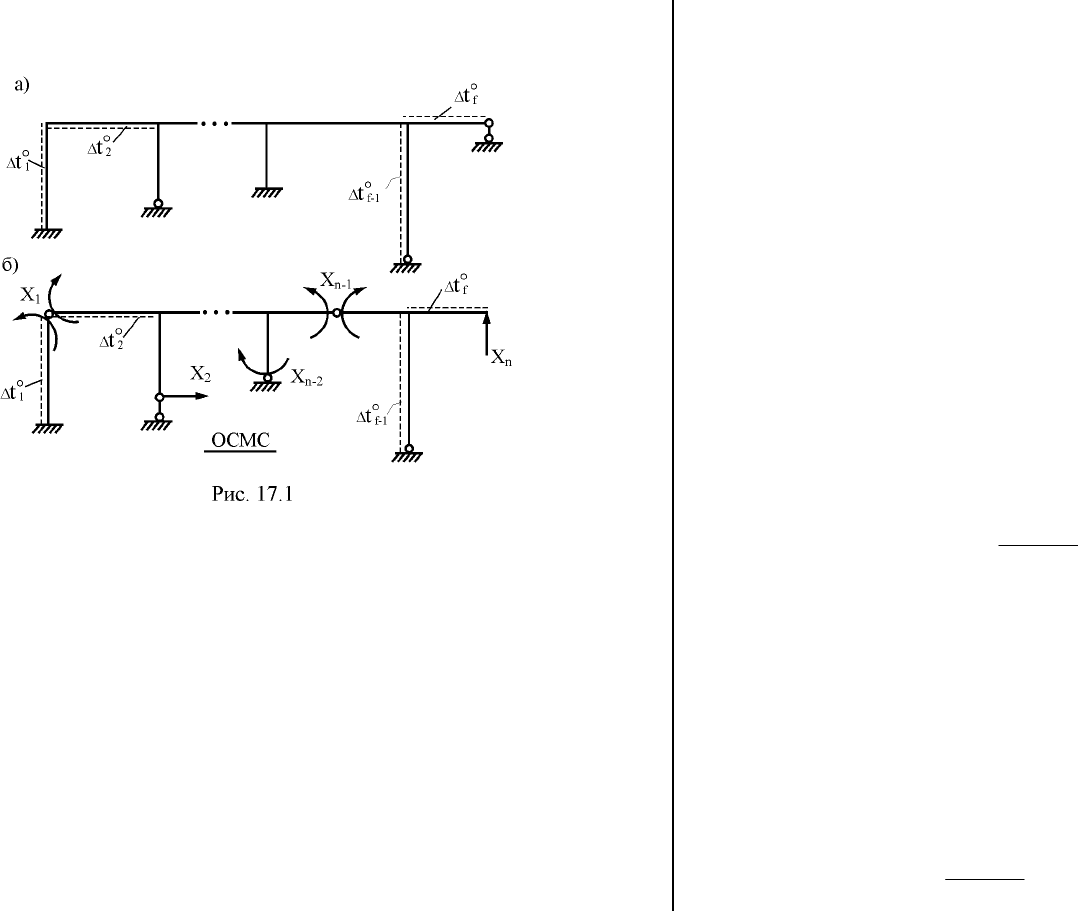
На плоскую стержневую систему,
степень статической неоп-
ределимости которой равна n (рис. 17.1,а) независимо друг от
друга действует f вариантов температурных полей. Каждое тем-
пературное поле характеризуется изменением температуры на
различных поверхностях элементов стержневой системы. На k-ом
участке любого элемента сооружения величины приращений
температуры
o
k
tΔ , коэффициента линейного температурного
расширения материала
α
k
, высоты поперечного сечения h
k
, а так-
же его жесткостных характеристик на изгиб EJ
k
, сдвиг GA
k
и рас-
тяжение–сжатие ЕА
k
будем считать постоянными. Закон измене-
99 100
ния приращений температуры по высоте поперечного сечения
примем линейным (см. п. 12.2 второй части настоящего курса
лекций).
Образуем статически определимую основную систему мето-
да сил (ОСМС), удалив из заданного сооружения n лишних свя-
зей (рис. 17.1,б). Неизвестные метода сил X
1
, X
2
, …, X
j
, …, X
n
оп-
ределим из условия эквивалентности напряжённо-деформируе-
мых состояний заданного сооружения (рис. 17.1,а) и его основной
системы (рис. 17.1,б), т.е. из условий равенства нулю перемеще-
ний по направлению X
i
(i = 1, 2, …, n) в основной системе метода
сил от неизвестных этого метода и заданного изменения темпера-
туры.
Используя принцип независимости действия сил и повторяя
выкладки, приведенные в п. 16.2 шестнадцатой лекции, получим
систему канонических уравнений для определения неизвестных
X
1
, X
2
, …, X
j
, …, X
n
в случае температурного воздействия на со-
оружение.
⎪
⎪
⎪
⎪
⎭
⎪
⎪
⎪
⎪
⎬
⎫
=Δ+δ+δ++δ++δ+δ
=Δ+δ+δ++δ++δ+δ
=Δ+δ+δ++δ++δ+δ
=Δ+δ+δ++δ++δ+δ
.0XXXXX
,0XXXXX
,0XXXXX
,0XXXXX
ntnnnjnjini22n11n
itninjijiii22i11i
t2nn2jj2ii2222121
t1nn1jj1ii1212111
KKK
KKKKKKKKKKKKKKKKKKKKK
KKK
KKKKKKKKKKKKKKKKKKKKK
KKK
KKK
(17.1)
Величина главных δ
ii
и побочных δ
ij
коэффициентов системы
канонических уравнений (17.1) не зависят от вида воздействия на
сооружения и определяются по ранее полученным в п. 16.2 фор-
мулам (16.5)–16.6) в общем случае плоских стержневых систем и
по формулам (16.8)–(16.9) для рам и балок.
Свободные члены системы канонических уравнений (17.1) Δ
it
представляют собой перемещения по направлению неизвестных
метода сил X
i
(i = 1, 2, …, n) в основной системе от заданного
температурного воздействия. Так как для расчёта принята стати-
чески определимая основная система, указанные перемещения в
ней определяются по формуле (12.4), полученной в п. 12.2 второй
части настоящего курса лекций:
∑
∫
∑
∫∫
==
Δα+
Δα
=Δ
NM
n
1k
0
k,okik
n
1k
0
k
k,nrk
ik
0
it
kkk
dst)s(Nds
h
t
)s(M
l
o
l
o
l
. (17.2)
В соотношении (17.2) M
ik
(s), N
ik
(s) – соответственно, изги-
бающие моменты и продольные силы на участке, где происходит
изменение температуры на величину
o
k
tΔ , от X
i
= 1 в основной
системе метода сил. Напоминаем читателям, что параметрами,
характеризующими температурное воздействие на k-ом участке,
являются:
o
k,nr
tΔ
– перепад приращений температуры по высоте
поперечного сечения;
o
k,0
tΔ – приращение температуры на уровне
центра тяжести поперечного сечения.
При наличии эпюр внутренних усилий M
ik
(s) и N
ik
(s), а также
условных эпюр
k
k,nrk
h
t
o
Δα
и
o
k,ok
tΔα , построенных вдоль про-

101 102
дольных осей элементов сооружения, интегралы, входящие в
формулу (17.2), можно вычислить, используя правило Верещаги-
на (см. п. 11.4 второй части настоящего курса лекций).
Жёсткости поперечных сечений элементов сооружения EJ
k
,
GA
k
, EA
k
учитываются при вычислении коэффициентов δ
ii
и δ
ij
системы канонических уравнений (17.1) и их значения не входят
в соотношение (17.2), с помощью которого вычисляются свобод-
ные члены указанной системы уравнений. Отсюда следует, что
величины усилий в лишних связях X
i
и, следовательно, внутрен-
них усилий в заданном сооружении являются функциями абсо-
лютных значений жесткостных характеристик поперечных сече-
ний стержней.
Получив значения усилий в лишних связях из системы урав-
нений (17.1), мы свели расчёт статически неопределимого соору-
жения (рис. 17.1,а) на температурное воздействие к расчёту ста-
тически определимой основной системы метода сил (
рис. 17.1,б),
на которую действуют указанные усилия X
1
, X
2
, …, X
i
, …, X
j
, …,
X
n
и заданное изменение температуры. Так как изменение темпе-
ратуры в статически определимых сооружениях внутренних уси-
лий не вызывает (см. п. 12.1 второй части настоящего курса лек-
ций), то значения изгибающих моментов M
t
, поперечных и про-
дольных сил Q
t
и N
t
в сечениях заданного сооружения в этой си-
туации определяются только усилия X
1
, X
2
, …, X
i
, …, X
j
, …, X
n
.
Имея эпюры внутренних усилий M
j
, Q
j
, N
j
от X
j
= 1 в основной
системе и используя принцип независимости действия сил, полу-
чим:
M
t
= M
1
X
1
+ M
2
X
2
+ … + M
j
X
j
+ … + M
n
X
n
,
Q
t
= Q
1
X
1
+ Q
2
X
2
+ … + Q
j
X
j
+ … + Q
n
X
n
, (17.3)
N
t
= N
1
X
1
+ N
2
X
2
+ … + N
j
X
j
+ … + N
n
X
n
.
Окончательные эпюры внутренних усилий M
t
, Q
t
, N
t
по-
строены правильно, если, выполнены кинематические условия:
перемещение по направлению любого усилия X
i
(i = 1, 2, …, n) в
отброшенных связях в основной системе от действия всех неиз-
вестных метода сил X
1
, X
2
, …, X
j
, …, X
n
и заданного температур-
ного воздействия должны быть равны нулю, так как в заданном
сооружении имеются связи, препятствующие перемещениям по
направлению X
i
.
Сопрягая проверяемые эпюры внутренних усилий M
t
, Q
t
, N
t
с
эпюрами внутренних усилий M
i
, Q
i
, N
i
, построенными в основной
системе от X
i
= 1, в соответствии с соотношениями (17.3) вычис-
лим перемещение по направлению X
i
в статически определимой
основной системе только от неизвестных метода сил X
1
, X
2
, …,
X
j
, …, X
n
. Добавляя к этому перемещению ещё и перемещение от
заданного изменения температуры Δ
it
, получим полное переме-
щение по направлению X
i
в основной системе, которое, если вы-
полняется кинематическая проверка, т.е. если поставленная зада-
ча решена правильно, должно быть равно нулю. Это возможно,
если перемещение по направлению X
i
в основной системе, вы-
званное неизвестными методами сил, будет компенсировано пе-
ремещением в том же направлении от заданного температурного
воздействия, т.е. будет равно (–Δ
it
). Таким образом,
it
n
1k
0
k
iktk
n
1k
0
k
iktk
n
1k
0
k
iktk
N
Q
M
k
kk
EA
ds)s(N)s(N
GA
ds)s(Q)s(Q
k
EJ
ds)s(M)s(M
Δ−=+
++
∑
∫
∑
∫
∑
∫
=
=
τ
=
l
ll
. (17.4)
В матричной форме система канонических уравнений (17.1)
запишется:
δХ + Δ
t
= 0. (17.5)
δ – матрица внешней податливости основной системы мето-
да сил по направлению усилий в отброшенных связях X
i
, или
матрица коэффициентов при неизвестных метода сил системы
канонических уравнений. Структура этой матрицы не зависит от
типа воздействия на заданное сооружение. Её элементы вычис-
ляются по формуле (16.21), полученной в п. 16.7 шестнадцатой
лекции.
Х – матрица неизвестных метода сил.

103 104
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
)f(
n
)2(
n
)1(
n
)f(
i
)2(
i
)1(
i
)f(
2
)2(
2
)1(
2
)f(
1
)2(
1
)1(
1
XXX
XXX
XXX
XXX
X
K
MMMM
K
MMMM
K
K
.
Δ
t
– матрица перемещений по направлению неизвестных ме-
тода сил в основной системе от заданного температурного воз-
действия, или матрица свободных членов системы канонических
уравнений (17.1).
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
ΔΔΔ
ΔΔΔ
ΔΔΔ
ΔΔΔ
=Δ
)f(
nt
)2(
nt
)1(
nt
)f(
it
)2(
it
)1(
it
)f(
t2
)2(
t2
)1(
t2
)f(
t1
)2(
t1
)1(
t1
t
K
MMMM
K
MMMM
K
K
.
Число строк в матрицах X и Δ
t
равно степени статической
неопределимости сооружения n, а число столбцов – числу вари-
антов задаваемых температурных воздействий f.
Элементы матрицы Δ
t
для статически определимой основной
системы вычисляются по формуле (17.2). В матричной форме со-
отношение (17.2) примет вид:
Δ
t
= TBL
t
T
t
. (17.6)
L
t
– матрица внутренних усилий (изгибающих моментов и
продольных сил), необходимых для расчёта сооружения на тем-
пературное воздействие в основной системе метода сил от Х
1
= 1,
Х
2
= 1, …, Х
j
= 1, …, Х
n
= 1.
L
t
= [L
t1
L
t2
… L
tj
… L
tn
];
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
o
o
tj
tj
tj
N
M
L
.
Для k-тых участков, где задано изменение температуры
o
k
tΔ = const, элементы блоков
o
tj
M и
o
tj
N фиксируются в средин-
ных сечениях этих участков.
B
t
– матрица температурной податливости сооружения.
⎥
⎦
⎤
⎢
⎣
⎡
=
o,t
nr,t
t
B0
0B
B
.
B
t,nr
– матрица температурной податливости сооружения при
неравномерных приращениях температуры; B
t,о
– то же при рав-
номерных приращениях температуры. Если для k-го участка
α
k
= const, h
k
= const, то
kk
)k(
o,t
k
kk
)k(
nr,t
B;
h
B l
l
α=
α
= .
Т – матрица приращений температур по вариантам воздейст-
вий.
Т = [Т
1
Т
2
… Т
j
… Т
f
];
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
j,o
j,nr
j
T
T
T
.
T
nr,j
и T
o,j
– соответственно, матрицы неравномерных и рав-
номерных приращений температур j-го варианта температурного
воздействия. Элементами этих матриц на k-ом участке изменения
температуры являются перепады приращений температур по вы-
соте поперечного сечения
o
k,nr
tΔ и приращения температуры в
центре тяжести поперечного сечения
o
k,o
tΔ
.
Из системы канонических уравнений (17.5) получим матрицу
неизвестных метода сил:
X = –δ
-1
Δ
t
. (17.7)
С учётом соотношений (16.21) и (17.6) матричное выражение
(17.7) перепишется в развёрнутой форме:
(
)
(
)
TBLLBLX
t
T
1
T
t
−
−= . (17.8)
Внутренние усилия M
t
, Q
t
, N
t
в заданном статически неопре-
делимом сооружении от температурного воздействия в матрич-
ной форме определим, используя формулы (17.3).
LX
N
Q
M
S
t
t
t
t
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
= . (17.9)
105 106
Напоминаем читателям, что L – матрица внутренних усилий,
необходимых для получения матрицы коэффициентов при неиз-
вестных метода сил δ системы канонических уравнений, в основ-
ной системе от X
1
= 1, X
2
= 1, …, X
j
= 1, …, X
n
= 1. Порядок фор-
мирования этой матрицы подробно изложен в п. 16.7 шестнадца-
той лекции.
С учётом выражения (17.8) матричное соотношение (17.9) в
окончательной форме примет вид:
()( )
TBLLBLLS
t
T
1
T
t
t
−
−= . (17.10)
В выражении (17.10) матрица В – это матрица внутренней
упругой податливости сооружения. Структура этой матрицы
подробно изложена в п. 16.7 шестнадцатой лекции.
Кинематическая проверка правильности расчёта заданного
статически неопределимого сооружения на температурное воз-
действие в матричной форме производится по формуле:
L
T
B S
t
= –Δ
t
. (17.1)
17.2. Пример расчёта статически неопределимой рамы
на температурное воздействие в обычной форме
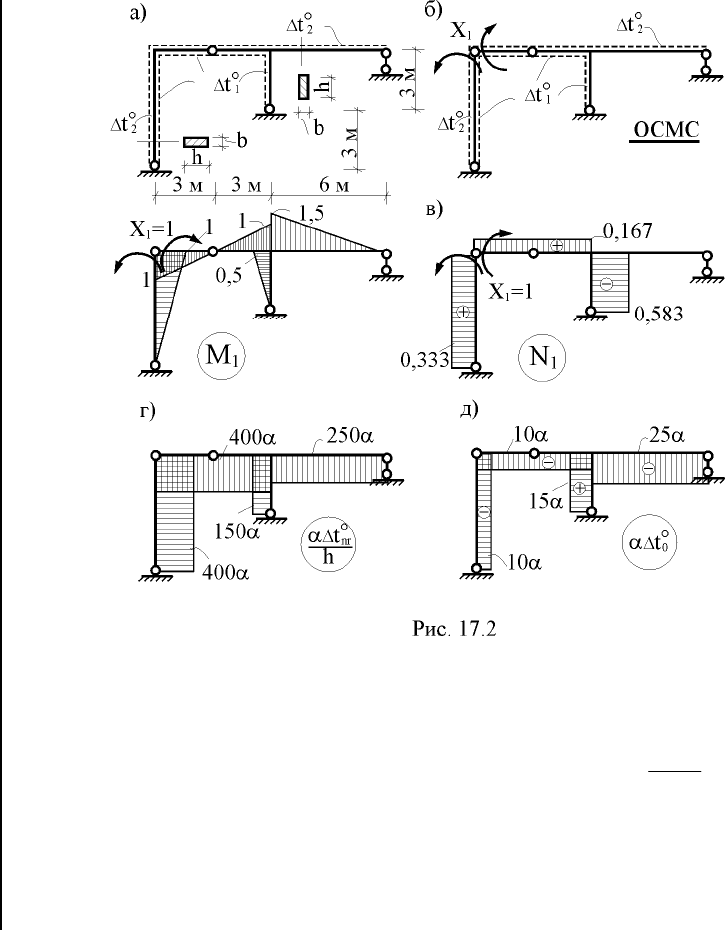
Со стороны внутренних волокон стержней левого контура
рамы (рис. 17.2,а) температура повысилась на
o
1
tΔ = 30 °С, со
стороны наружных волокон левой стойки и верхних волокон ри-
геля температура понизилась на
o
2
tΔ = -50 °С. Поперечные сече-
ния элементов рамы прямоугольные размером b×h (h = 0,2 м).
Коэффициент линейного температурного расширения материала,
из которого изготовлены стержни рамы, известен и равен α. Тре-
буется построить эпюры внутренних усилий от заданного темпе-
ратурного воздействия.
1. Определение степени статической неопределимости рамы:
n
st
= 3К – Н = 3 ⋅ 2 – 5 = 1.
2. Выбор статически определимой основной системы метода
сил. Лишнюю связь заданной рамы удалим путём введения ци-
линдрического шарнира в её верхний левый узел (рис. 17.2,б).
Читателям предлагается произвести кинематический анализ по-
лученной основной системы и убедиться в её геометрической не-
изменяемости.
3. Построение эпюры изгибающих моментов М
1
и эпюры
продольных сил N
1
в основной системе от Х
1
= 1 (рис. 17.2,в).
4. Построение условных эпюр, связанных с перепадами при-
ращений температур по высоте поперечного сечения
h
t
nr
o
Δα
и
приращениями температур на уровне центров тяжести попереч-
ных сечений
o
o
tΔ (рис. 17.2,г,д). При построении этих эпюр учте-
но, что h = 0,2 м, и приняты во внимание следующие численные
значения величин
o
nr
tΔ
и
o
o
tΔ
:

107 108
– для левого ригеля и левой стойки:
o
nr
tΔ = 30 – (–50) = 80 °С,
o
o
tΔ =
2
5030 −
= –10 °С;
– для правого ригеля:
o
nr
tΔ = 0 – (–50) = 50 °С,
o
o
tΔ =
2
500 −
= –25 °С;
– для правой стойки:
o
nr
tΔ
= 30 – 0 = 30 °С,
o
o
tΔ
=
2
300 +
= 15 °С.
Ординаты эпюры
h
t
nr
o
Δα
отложены со стороны более "тёп-
лых" волокон, на эпюре же α
o
o
tΔ зафиксирован знак "плюс" на
элементах с положительными приращениями температур на
уровне центров тяжести поперечных сечений и знак "минус" – с
отрицательными (см. п. 12.2 и пример 12.2.1 второй части на-
стоящего курса лекций).
5. Вычисление коэффициентов разрешающего уравнения ме-
тода сил
δ
11
Х
1
+ Δ
1t
= 0. (17.1,а)
Как и при силовом воздействии, в рамных системах коэффи-
циент δ
11
вычисляется без учёта влияния на величину искомого
перемещения деформаций сдвига и растяжения–сжатия.
,
EJ
75,8
5,1
3
2
5,16
2
1
EJ
1
5,0
3
2
5,03
2
1
EJ
1
)1111(
EJ6
6
1
3
2
16
2
1
EJ
1
ds)s(M
EJ
1
4
1k
0
2
k1
k
11
k
=⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅+
+⋅+⋅+⋅⋅⋅⋅⋅==δ
∑
∫
=
l
где
12
bh
EJ
3
= .
Перемещение по направлению Х
1
от заданного изменения
температуры в основной системе определим по формуле (17.2),
вычисляя определённые интегралы сопряжением эпюры М
1
с
эпюрой
h
t
nr
o
Δα
и эпюры N
1
с эпюрой α
o
o
tΔ .
.26,13115583,03
10167,0610333,062505,16
2
1
1505,03
2
1
)40014001(
6
6
40016
2
1
dst)s(N
h
dst
)s(M
4
1k
0
k,okk1
4
1k
0
k
k,nrk
k1t1
kk
α=α⋅⋅−
−α⋅⋅−α⋅⋅−α⋅⋅⋅−
−α⋅⋅⋅+α⋅−α⋅+α⋅⋅⋅=
=Δα+
Δα
=Δ
∑
∫
∑
∫
==
l
o
l
o
6. Вычисление неизвестного метода сил из уравнения
(17.1,а):
.EJ15
75,8
EJ26,131
X
11
t1
1
α
−
=
=
α
−=
δ
Δ
−=
7. Определение изгибаю-
щих моментов в сечениях за-
данной рамы от температурно-
го воздействия и построение
эпюры M
t
(рис. 17.3,а). Из
первого выражения соотноше-
ний (17.3) имеем:
M
t
= M
1
X
1
,
где Х
1
= –15αEJ.
8. Кинематическая про-
верка решения задачи. Для
этой проверки используем
формулу (17.4), в которой со-
храним только первый член,
ибо коэффициент δ
11
выше
нами был определён только с
учётом деформаций изгиба.
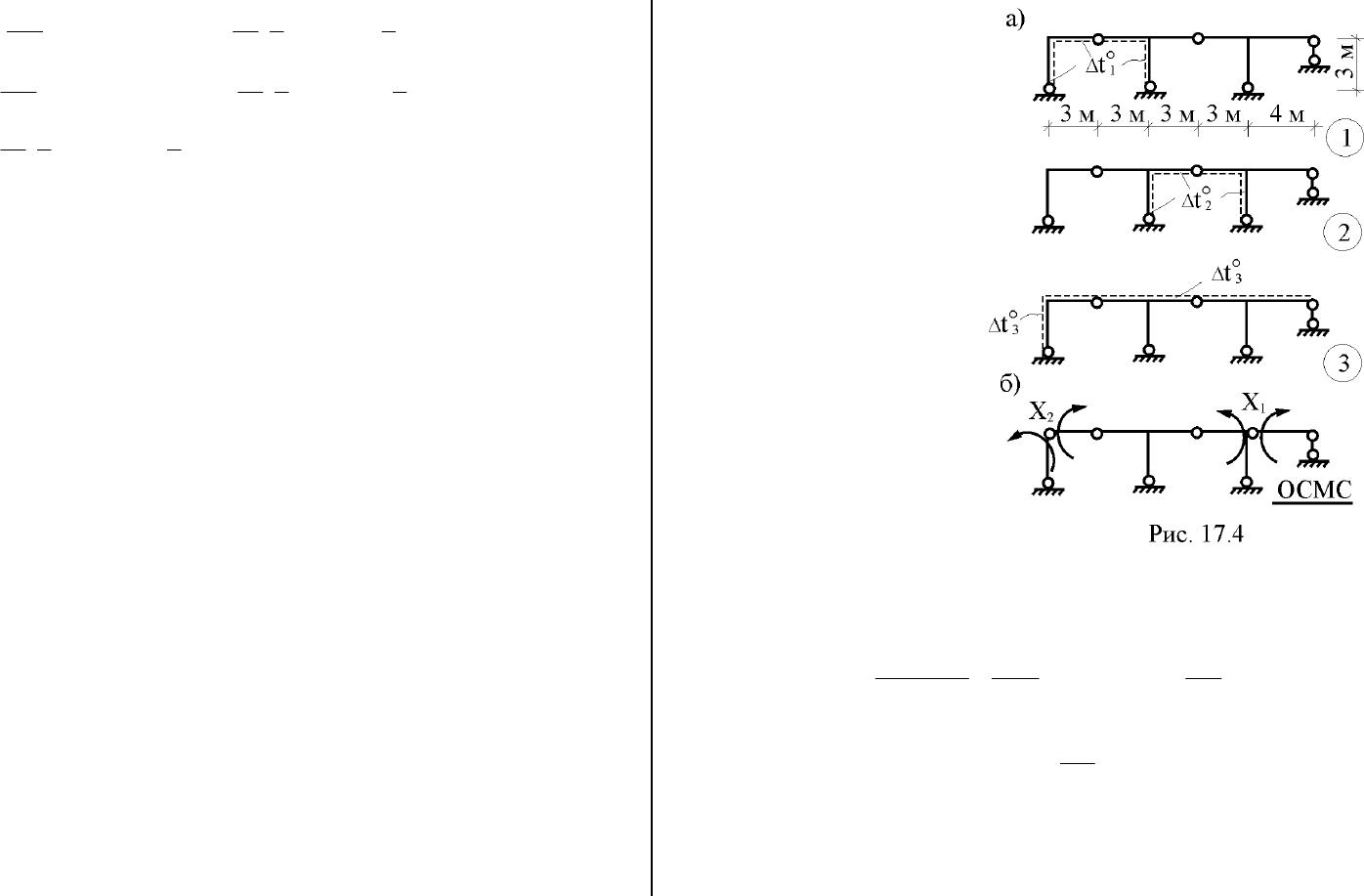
109 110
.EJ25,1315,1
3
2
EJ5,226
2
1
EJ
1
5,0
3
2
EJ5,73
2
1
EJ
1
)EJ151EJ151(
EJ6
6
1
3
2
EJ156
2
1
EJ
1
ds)s(M)s(M
EJ
1
4
1k
0
k1tk
k
k
α−=⋅⋅α⋅⋅⋅−
−⋅⋅α⋅⋅⋅−α⋅+α⋅−
−⋅⋅α⋅⋅⋅−=
∑
∫
=
l
Результат сопряжения эпюр M
t
и М
1
практически совпал с
численным значением правой части разрешающего уравнения
(17.1,а)
δ
11
X
1
= –Δ
1t
,
что подтверждает правильность решения поставленной задачи.
9. Построение обычным порядком эпюры поперечных сил Q
t
(рис. 17.3,б) и эпюры продольных сил N
t
(рис. 17.3,в). В нашей
задаче окончательную эпюру продольных сил N
t
можно также
получить, используя последнее выражение соотношения (17.3),
которое для рассматриваемой задачи примет вид:
N
t
= N
1
Х
1
.
Обращаем внимание читателя на то, что ординаты оконча-
тельных эпюр внутренних усилий (М
t
, Q
t
, N
t
) зависят от абсолют-
ного значения изгибной жёсткости поперечного сечения элемен-
тов рамы EJ.
17.3. Пример расчёта статически неопределимой рамы
на температурное воздействие в матричной форме
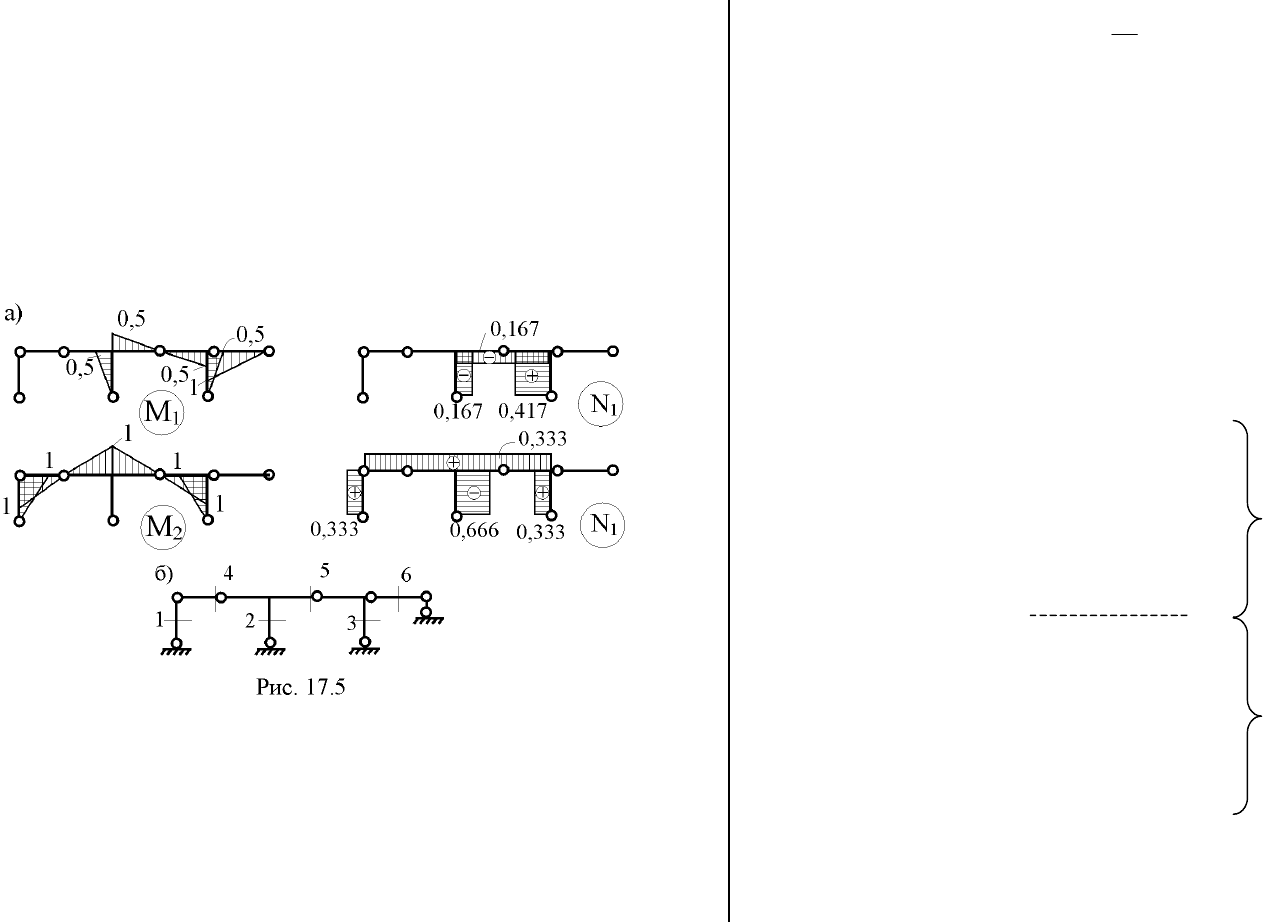
В статически неопределимой раме (рис. 17.4,а) возможны
следующие независимые друг от друга варианты температурных
воздействий: первый – повышение температуры со стороны
внутренних волокон стержней левого контура на
o
1
tΔ = 120 °С,
второй – повышение температуры со стороны внутренних воло-
кон элементов среднего контура на
o
2
tΔ = 80 °С, третий – пони-
жение температуры со стороны наружных волокон левой стойки
и ригелей на
o
3
tΔ = –40 °С. Ширина прямоугольных поперечных
сечений стоек и ригелей рамы одинакова и равна b; высота попе-
речного сечения стойки h
c
= h, ригеля – h
p
= 1,587h (h = 0,3 м).
Коэффициент линей-
ного температурного
расширения материала,
из которого изготовле-
ны элементы рамы, ра-
вен α. Требуется по-
строить эпюры внут-
ренних усилий в за-
данной раме от каждо-
го из вышеперечис-
ленных вариантов
температурных воз-
действий.
Размеры прямо-
угольных поперечных
сечений рамы заданы
так, что сохраняется
соотношение изгибных
жесткостей
попереч-
ных сечений ригелей и
стоек, принятое для
расчёта этой же рамы,
в матричной форме на силовое воздействие в п. 16.8 шестнадца-
той лекции, а именно: EJ
p
: EJ
c
= 2 : 0,5. Приняв EJ
p
= 2 EJ,
EJ
с
= 0,5 EJ, получим численное значение жесткостного парамет-
ра EJ:
(
)
EJ5,0
12
bh
EJ,EJ2
12
bh4
12
h587,1b
EJ
3
c
3
3
p
===== .
Каждое из этих соотношений даёт
6
bh
EJ
3
=
.
Для расчёта рамы на температурное воздействие в матрич-
ной форме используем соотношение (17.10), в котором примем
L = M, B = B
M
, S
t
= M
t
, так как вычисление матрицы внешней жё-
сткости принятой основной системы метода сил (рис. 17.4,б) бу-
111 112
дем производить только с учётом изгибных деформаций. В этом
случае матричное выражение (17.10) перепишется:
M
t
= –M(M
T
B
M
M)
-1
(L
T
t
B
t
T).
1. Определение степени статической неопределимости рамы
и выбор основной системы метода сил (рис. 17.4,б). Основная
система для расчёта рамы на температурное воздействие будет
такой же, как и при её расчёте на силовое воздействие в матрич-
ной форме (см. п. 16.8 шестнадцатой лекции).
2. Построение эпюр изгибающих моментов и продольных
сил в основной
системе метода сил от Х
1
= 1 и Х
2
= 1 (рис. 17.5,а).
Эпюры изгибающих моментов М
1
и М
2
от этих воздействий бы-
ли получены ранее (см. п. 16.8, рис. 16.14,в,г).
3. Формирование матрицы изгибающих моментов М от
Х
1
= 1 и Х
2
= 1 в основной системе и матрицы внутренней упру-
гой податливости В
М
в соответствии с принятой на рис. 16.16
нумерацией грузовых участков и сечений (см. п. 16.8 шестнадца-
той лекции).
5. Вычисление элементов матрицы внешней податливости
принятой для расчёта основной системы метода сил (см. п. 16.8
шестнадцатой лекции).
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
650,0
50,092,1
EJ
1
MBM
M
T
.
6. Обращение матрицы внешней податливости рамы (см.
п. 16.8 шестнадцатой лекции).
()
⎥
⎦
⎤
⎢
⎣
⎡
=
−
170,0044,0
044,0533,0
EJMBM
1
M
T
.
7. Нумерация участков и сечений для формирования матри-
цы изгибающих моментов и продольных сил от Х
1
= 1, Х
2
= 1 в
основной системе L
t
, матрицы температурной податливости со-
оружения B
t
и матрицы приращений температур Т (рис. 17.5,б).
Заметим, что при расчёте рамы на температурное воздействие
номера участков и их срединных сечений совпадают.
8. Формирование матрицы L
t
по эпюрам внутренних усилий
M
1
, N
1
, M
2
, N
2
(рис. 17.5,а) в соответствии с принятой нумерацией
срединных сечений.
o
o
o
o
o
o
o
o
o
o
o
o
o
o
6,t
5,t
4,t
3,t
2,t
1,t
6,t
5,t
4,t
3,t
2,t
1,t
t
t
t
N
N
N
N
N
N
M
M
M
M
M
M
00
333,0167,0
333,00
333,0417,0
666,0167,0
333,00
05,0
00
00
5,025,0
025,0
5,00
N
M
L
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−−
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
o
t
M
o
t
N
9. Формирование матрицы температурной податливости со-
оружения B
t
в соответствии с принятой нумерацией участков
(рис. 17.5,б).
113 114
⎥
⎦
⎤
⎢
⎣
⎡
=
0,t
nr,t
t
B0
0B
B,
где
[
]
)6(
nr,t
)5(
nr,t
)4(
nr,t
)3(
nr,t
)2(
nr,t
)1(
nr,t
nr,t
BBBBBBdiagB = ,
[
]
)6(
0,t
)5(
0,t
)4(
0,t
)3(
0,t
)2(
0,t
)1(
0,t
0,t
BBBBBBdiagB =
,10BBB,10
3,0
3
h
B
)1(
nr,t
)3(
nr,t
)2(
nr,t
c
1
)1(
nr,t
α===α=
α
=
α
=
l
,61,12BB,61,12
3,0587,1
6
h
B
)4(
nr,t
)5(
nr,t
p
4
)4(
nr,t
α==α=
⋅
α
=
α
=
l
α=
⋅
α
=
α
= 41,8
3,0587,1
4
h
B
p
6
)6(
nr,t
l
;
,3BBB,3B
)1(
0,t
)3(
0,t
)2(
0,t
1
)1(
0,t
α===α=α= l
α=α=α==α=α= 4B,6BB,6B
6
)6(
0,t
)4(
0,t
)5(
0,t
4
)4(
0,t
ll .
.
4
6
6
3
3
3
4,8
61,12
61,12
10
10
10
B
t
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
α=
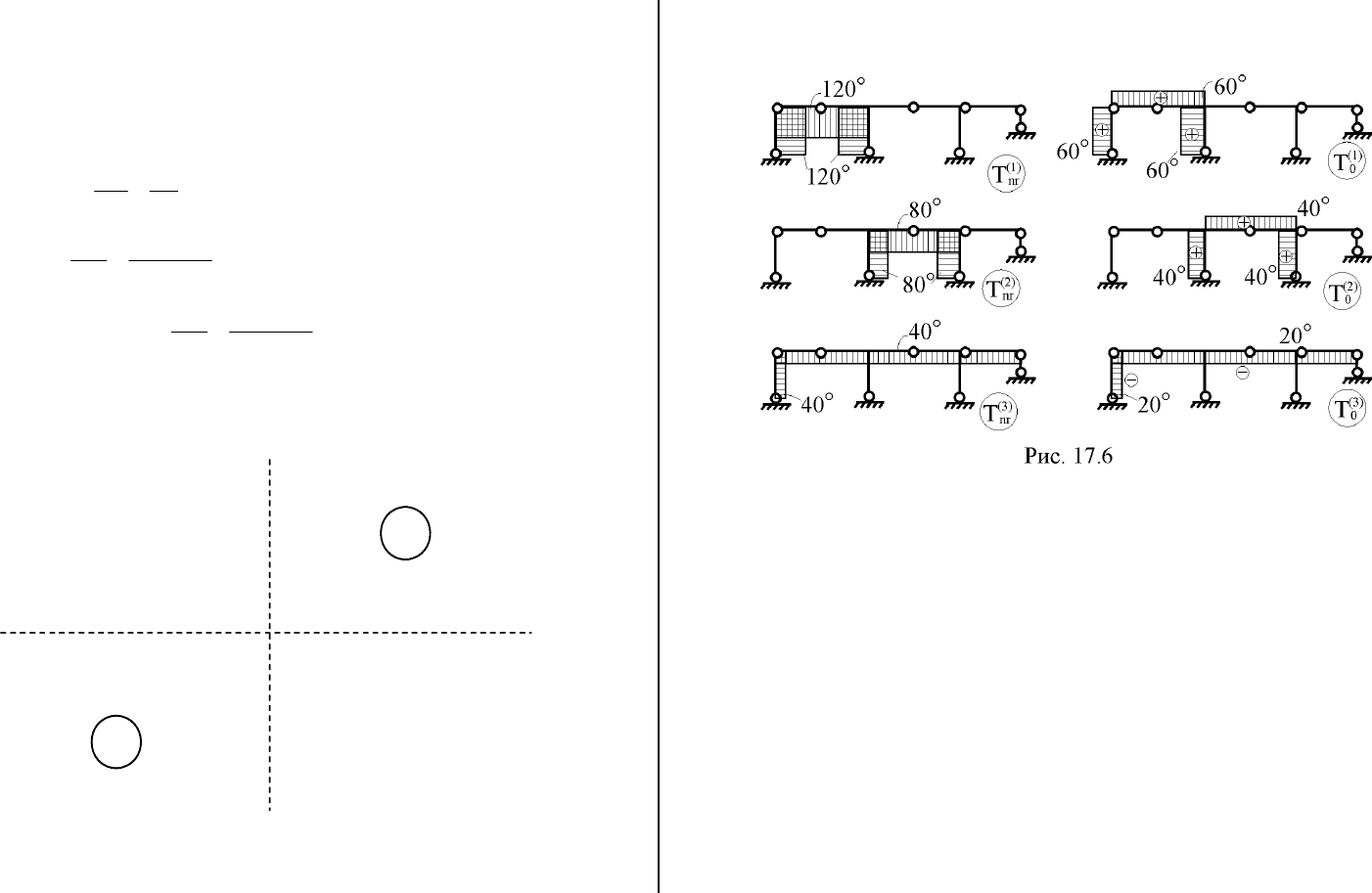
10. Построение эпюр неравномерных (T
nr
) и равномерных
приращений температур (Т
0
) по вариантам воздействий
(рис. 17.6).
Ординатами этих эпюр (соответственно, и элементами мат-
риц T
nr
и T
0
) на k-том участке являются перепад приращений
температур по высоте поперечного сечения
o
k,nr
tΔ и приращение
температуры в центре тяжести поперечного сечения
o
k,0
tΔ . Чис-
ленное значение величин
o
k,nr
tΔ
и
o
k,0
tΔ
по вариантам воздействий
читателям предлагается получить самостоятельно.
11. Формирование матрицы приращений температур Т по ва-
риантам воздействий (рис. 17.6) в соответствии с принятой нуме-
рацией участков. Правило знаков для элементов матрицы T
nr
сов-
падает с правилом знаков для элементов матрицы М (см. пример
13.4.1 тринадцатой лекции). Знаки элементов подматрицы Т
0
совпадает со знаком приращений температуры в центрах тяжести
поперечных сечений
o
k,0
tΔ , т.е. со знаками эпюры Т
0
на рассмат-
риваемых участках.
