Крамаренко А.А., Широких Л.А. Лекции по строительной механике стержневых систем. Часть 3: Статически неопределимые системы. Метод сил

Подождите немного. Документ загружается.

39 40

лённую нагрузку, при постоянной изгибной жёсткости попереч-

ного сечения EJ на этом участке? Как запишется матрица В

для

участка, где нет распределённой нагрузки, при тех же условиях?

4. Для загруженной сосредоточенными силами в узлах фер-

мы требуется вычислить заданную преподавателем матрицу пе-

ремещений. Какое матричное соотношение необходимо исполь-

зовать для решения этой задачи? Поясните смысл элементов мат-

риц N

, B

, N

. Сколько строк и столбцов будет в этих матрицах?

Какой вид будет иметь матрица B

для конкретного стержня

фермы?

5. Как в матричной форме от силового воздействия вычис-

ляются матрицы перемещений в плоских комбинированных сис-

темах? Какой смысл имеют элементы матриц L

, B и L

? Из ка-

ких блоков состоят эти матрицы? Как формируются отдельные

блоки этих матриц: M

, N

, B

, M

, N

6. Запишите матричное соотношение для определения мат-

риц перемещений в произвольных плоских стержневых системах

от силового воздействия. Поясните для этого случая структуру

матриц L

, B и L

. Как формируются блоки Q

, B

, входящие в

состав матриц L

, B и L

, на отдельных грузовых участках? От че-

го зависит структура этих блоков?

7. Какую структуру имеют матицы L

, B и L

для пространст-

венных стержневых систем в самом общем случае ?

8. Задана плоская стержневая система (балка, рама, ферма

или комбинированная). Запишите матричное соотношение для

определения перемещения в ней от температурных воздействий.

Какую структуру имеют матрицы L

, B

и T, входящие в эти соот-

ношения? Поясните смысл элементов подматриц M

, N

, B

tn,r

, B

t,0

, T

. Какой размер имеет любая из этих подматриц для задан-

ной системы?

9. В балочной или рамной системе часть опорных связей по-

лучила смещение на заданную величину. Как от этого воздейст-

вия вычислить элементы заданной преподавателем матрицы пе-

ремещений в матричной форме? Какой смысл имеют элементы

матриц R

и Δ

(с)

? Каковы размеры этих матриц? Сформулируйте

правило знаков, используемые при формировании матрицы R

10. Какое матричное соотношение используется для вычис-

ления заданной матрицы перемещений в случае независимых

друг от друга силовых, температурных и кинематических воздей-

ствий на сооружение? Из каких блоков состоят матрицы L

, B

∑

, необходимые для решения поставленной задачи? Запишите

эти матрицы в блочной форме и поясните смысл элементов под-

матриц L

, L

, R

, B, B

, E, L

, T, Δ

(с)

13.9. Рекомендуемая литература

1. Леонтьев Н.Н. Основы строительной механики стержневых систем:

Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.:

Изд-во ассоциации строительных вузов, 1996. – 541 с.

Гл. 5. Основы теории расчёта линейно деформируемых систем.

§ 5.7. Способы вычисления интегралов Мора. – С. 115.

2. Смирнов А.Ф. Строительная механика. Стержневые системы:

Учеб. для

вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащени-

ков, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.

Гл. VIII. Определение перемещений по методу Мора. § 43. Матрич-

ная форма определения перемещений по методу Мора. – С. 226–

238.

3. Клейн Г.К. Руководство к практическим занятиям по курсу строи-

тельной механики. Статика стержневых систем: Учеб. пособие /

Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.

Гл. VIII. Потенциальная энергия упругих систем. Определение пе-

ремещений стержневых систем. § VIII.9. Матричная форма опреде-

ления перемещений. – С. 130–136.

4. Проценко В.М. Расчёт статически определимых систем: Метод.

указания к контрольным работам по строительной механике /

В.М. Проценко, В.Г. Себешев. – Новосибирск: НИСИ, 1990. – 52 с

Задача № 6. Определение перемещений в статически определимой

раме. – С. 43–47.

41 42

ЛЕКЦИЯ ЧЕТЫРНАДЦАТАЯ

ОБЩИЕ СВЕДЕНИЯ О СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ

СИСТЕМАХ

14.1. Характеристика статически неопределимых сис-

тем и некоторые их свойства

14.2. Степень статической неопределимости

14.3. Методы расчёта статически неопределимых

систем

14.4. Вопросы для самопроверки

14.5. Рекомендуемая литература

14.1. Характеристика статически неопределимых

систем и некоторые их свойства

Расчёт сооружений на прочность, жёсткость и устойчивость

требует определения

реакций опорных связей и внутренних уси-

лий в характерных сечениях их элементов. В статически неопре-

делимых системах эту задачу, привлекая только условия равнове-

сия, решить невозможно. Это было показано в сопротивлении

материалов, где для расчёта отдельных статически неопредели-

мых стержней, работающих на растяжение–сжатие, кручение, из-

гиб, использовалась группа соотношений, включающая

в себя

уравнения равновесия, геометрические и физические уравнения.

Главной особенностью статически неопределимых систем

является наличие лишних связей в их структуре. Лишние связи

сооружений можно удалять, не нарушая их геометрической не-

изменяемости. Например, удалением опорных вертикальных свя-

зей В и С неразрезная балка преобразуется в консольный стер-

жень, введением цилиндрических шарниров K

и L – в статически

определимую двухпролётную составную балку (рис. 14.1,а). Уда-

лив из статически неопределимой фермы стержень 14 или 34, по-

лучим два варианта статически определимой шарнирно-

стержневой системы с простой структурой (рис. 14.1,б). Статиче-

ски неопределимая двухшарнирная рама после удаления горизон-

тальной связи опоры В превращается в ломаный стержень, при-

креплённый к диску

"земля" шарниром А и вертикальной связью,

ось которой не проходит через шарнир А. Введением цилиндри-

ческого шарнира С эта же рама преобразуется в статически опре-

делимую трёхшарнирную раму (рис. 14.1,в).

Особенностью всех лишних связей, удалённых из статически

неопределимых систем, показанных слева на рис. 14.1, является

то, что реакции в них от внешних воздействий с помощью урав-

нений статики определить нельзя. Эти связи называются условно

необходимыми. Вместе с тем, в составе рассмотренных сооруже-

ний имеются связи, усилия в которых определяются из условий

равновесия: горизонтальная связь опоры А неразрывной балки

(рис. 14.1,а), стержни А

2,23, А1, А3 фермы (рис. 14.1,б), верти-

кальные связи пятовых шарниров А и В рамы (рис. 14.1,в). Такие

связи называются абсолютно необходимыми. Их удаление пре-

вращает заданное сооружение в геометрически изменяющую или

мгновенно изменяемую систему.

Отметим некоторые свойства статически неопределимых

систем.

1. Статически неопределимые сооружения обладают боль-

шей надёжностью по сравнению со статически определимыми

Действительно, выключение из работы статически неопредели-

мых систем одной или всех лишних условно необходимых связей

43 44

не нарушает их геометрической неизменяемости. В статически

определимых системах удаление только одной связи приводит к

образованию механизмов с одной степенью свободы.

2. В статически неопределимых системах от температурных

и кинематических воздействий реакции условно необходимых

внешних и внутренних

связей не равны нулю.

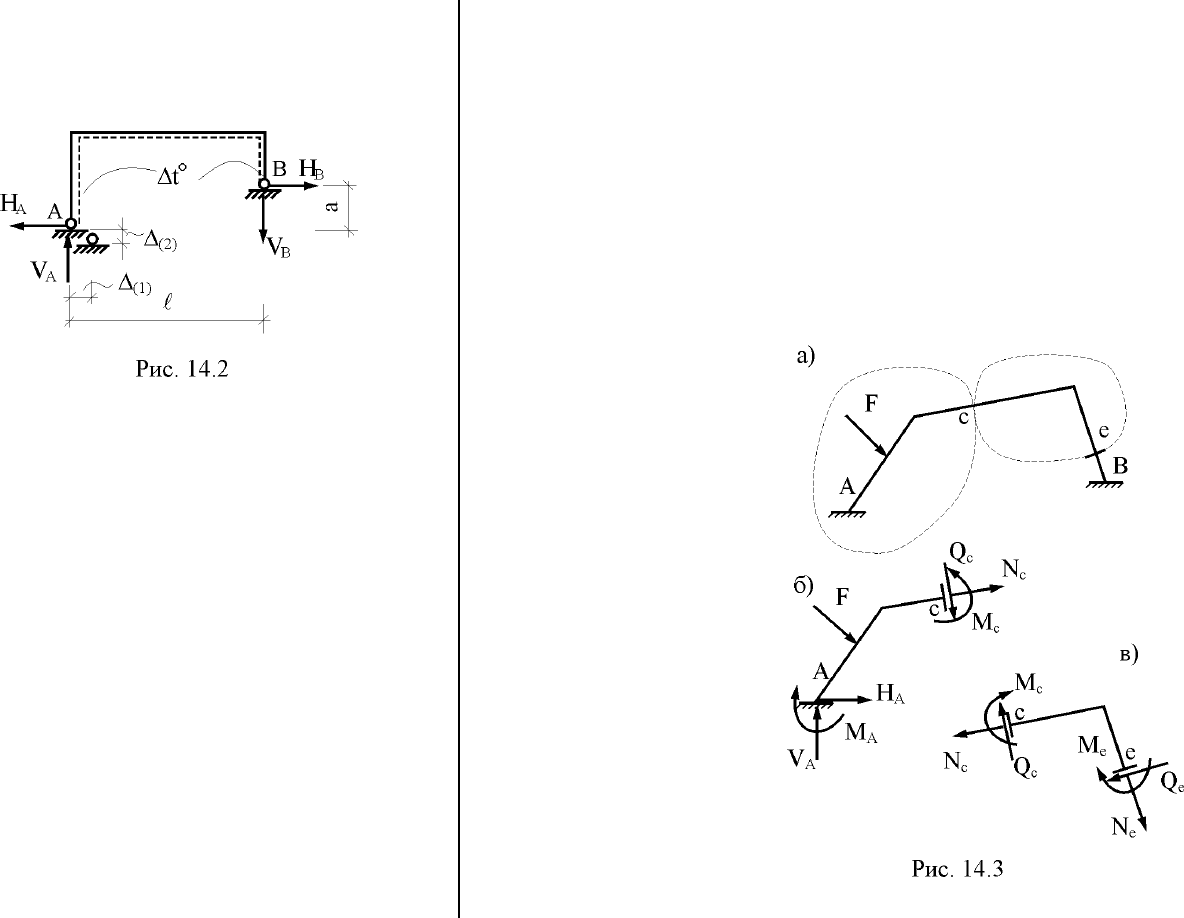
Покажем это на примере

определения реакций

опорных связей двухшар-

нирной

рамы с пятовыми

шарнирами на разных

уровнях (рис. 14.2). Пусть

температура со стороны

внутренних волокон эле-

ментов рамы изменилась на Δt°, а горизонтальная и вертикальная

связи левой шарнирно-неподвижной опоры сместились соответ-

ственно на Δ

(1)

и Δ

(2)

. Условия равновесия рамы имеют вид:

∑ F

= 0, H

– H

= 0,

∑ F

= 0, V

– V

= 0,

∑mom (F)

= 0, H

⋅ a + V

⋅ ℓ = 0.

Полученная система трёх уравнений, содержащая четыре не-

известных, в общем случае имеет ненулевые решения. От реак-

ций шарнирно-неподвижных опор в сечениях рамы возникнут из-

гибающие моменты, поперечные и продольные силы. Таким об-

разом, в отличие от статически определимых систем в статически

неопределимых системах от температурных и кинематических

воздействий имеют место не только перемещения, но и деформа-

ции, вызывающие внутренние усилия.

Остальные свойства статически неопределимых систем бу-

дут сформулированы и обоснованы в последующих лекциях.

14.2. Степень статической неопределимости

Разность между числом неизвестных, необходимых для рас-

чёта заданного сооружения, и числом независимых уравнений

равновесия, составленных для решения задачи, называется степе-

нью статической неопределимости сооружения. Другими слова-

ми, эта разность определяет количество лишних связей в задан-

ной расчётной схеме сооружения, усилия в которых требуется

определить, не прибегая к уравнениям равновесия.

Степень статической неопределимости можно вычислить,

преобразуя заданную статически неопределимую систему в ста-

тически определимую и параллельно подсчитывая число удалён-

ных связей. Такой

подход является наиболее общим, но часто у

читателей вызывает определённые трудности. Поэтому в плоских

стержневых системах на начальном этапе изучения этой и после-

дующих тем степень статической неопределимости рекомендует-

ся определять по формуле "контуров".

Любой замкнутый плоский стержневой контур содержит три

лишних связи, т.е.

трижды статически

неопределим. В этом

можно убедиться,

рассматривая опре-

деление внутренних

усилий в сечении "с"

рамы, представляю-

щей собой вместе с

диском "земля" замк-

нутый контур

(рис. 14.3,а). Любая

отсечённая часть

этой рамы имеет

шесть неизвестных:

рис. 14.3,б – внут-

ренние усилия в се-

чении "с" M

, Q

, N

реакции заделки V

, M

; рис. 14.3,в –

внутренние усилия в

сечениях "с" и "е" M

, N

, M

, Q

, N

. Равновесие рассматриваемых выше отсечённых

45 46

частей описывается тремя уравнениями. Таким образом, разность

между числом неизвестных, необходимых для описания напря-

жённо-деформированного состояния рамы, и числом уравнений

равновесия равно трём.

Если сооружение состоит из К не накладывающихся друг на

друга контуров, то общее число лишних связей в нём равно 3К.

Наличие в одноконтурном сооружении одного простого ци-

линдрического или поступательного шарнира снижает степень

статической неопределимости такого сооружения на единицу, так

как любая отсечённая часть контура, включающая в себя сечение,

расположенное на бесконечно близком расстоянии от шарнира,

будет содержать теперь пять, а не шесть, неизвестных (рис. 14.4).

Напомним читателям, что простой цилиндрический или

поступа-

тельный шарнир связывает только два диска. Если шарнир со-

единяет n дисков, то он эквивалентен n–1 простому шарниру

(см. п. 2.3 части 1 настоящего курса лекций).

В общем случае, если К контуров имеют Н простых цилинд-

рических или поступательных шарниров, то степень статической

неопределимости сооружения равна

= 3K – H. (14.1)

Число контуров и простых шарниров зависит от способа

представления расчётной схемы сооружения. На рис. 14.5,а,б по-

казано изображение расчётной схемы одной и той же рамы с раз-

личным количеством контуров и простых шарниров. Естествен-

но, что степень статической неопределимости рамы не зависит от

способа изображения её расчётной схемы. Действительно:

= 3 ⋅ 3 – 3 = 6 (рис. 14.5,а),

= 3 ⋅ 5 – 9 = 6 (рис. 14.5,б).

47 48

П РИМЕР 14.2.1. Используя формулу "контуров", вычис-

лить степень статической неопределимости плоских стержневых

систем, изображённых на рис. 14.6.

На рис. 14.6,а,б цифрами, объединёнными кружками, прону-

мерованы замкнутые контуры. Рядом с цилиндрическими шарни-

рами цифрами помечено количество простых шарниров.

= 3 ⋅ 3 – 8 = 1 (рис. 14.6,а),

= 3 ⋅ 9 – 24 = 3 (рис. 14.6,б).

14.3. Методы расчёта статически неопределимых

систем

Для расчёта статически неопределимых систем используют-

ся следующие методы:

1. Метод сил.

2. Метод перемещений.

3. Комбинированный метод расчёта симметричных систем.

4. Смешанный метод.

5. Метод конечных элементов.

6. Приближённые методы (метод последовательных при-

ближений и др.).

Подробное изложение сути этих

методов дано ниже в на-

стоящем (метод сил) и последующих изданиях лекций (осталь-

ные методы).

14.4. Вопросы для самопроверки

1. Какие системы называются статически неопределимыми?

2. Какие связи сооружения называются условно необходи-

мыми? Абсолютно необходимыми? К чему приводит удаление из

сооружения хотя бы одной абсолютно необходимой связи?

3. Задана плоская статически

неопределимая система. Со-

держит ли эта система абсолютно необходимые связи? Если да,

то дайте этим связям статическую и кинематическую характери-

стику.

4. Задано температурное или кинематическое воздействие

(смещение одной из опорных связей) на простейшую статически

неопределимую систему. Докажите, что от указанных воздейст-

вий в сечениях этой системы будут иметь место

внутренние уси-

лия.

5. Почему статически неопределимые системы по сравне-

нию со статически определимыми обладают более высокой на-

дёжностью?

6. Что называется степенью статической неопределимости

сооружения?

7. Сформулируйте общий принцип определения степени

статической неопределимости сооружения.

8. Запишите формулу "контуров" для определения степени

статической неопределимости сооружения. Поясните, как опре-

деляется число простых

цилиндрических и поступательных шар-

ниров Н, используемое в этой формуле?

9. Что называется простым цилиндрическим или поступа-

тельным шарниром? Как определяется число простых шарниров

в случае, когда осуществляется шарнирное сочленение несколь-

ких дисков в одном узле?

10. Почему бесшарнирный замкнутый контур трижды ста-

тически неопределим? Почему введение цилиндрического или

поступательного

шарнира в такой контур снижает его степень

статической неопределимости на единицу?

11. Задана плоская статически неопределимая система. Оп-

ределите степень статической неопределимости её, используя

общий принцип или формулу "контуров". Преобразуйте эту сис-

тему в статически определимую, удаляя, по своему усмотрению,

лишние связи.

14.5. Рекомендуемая литература

1. Леонтьев Н.Н. Основы строительной механики стержневых систем:

Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.:

Изд-во ассоциации строительных вузов, 1996. – 541 с.

Гл. 5. Основы теории расчёта линейно деформируемых систем.

§ 5.1. Общая характеристика методов расчёта статически неопре-

делимых систем. – С. 94–96.

2. Дарков А.В. Строительная механика:

Учеб. для вузов / А.В. Дар-

ков, Н.Н. Шапошников. – М.: Высш. школа, 1986. – 607 с.

49 50

Гл. 6. Расчёт статически неопределимых систем методом сил.

§ 6.1. Статическая неопределимость. – С. 193–199.

3. Смирнов А.Ф. Строительная механика. Стержневые системы:

Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лаще-

ников, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с.

Гл. XI. Метод сил. § 57. Особенности расчёта статически неопре-

делимых систем. § 58. Определение степени статической неопре

делимости. – С. 309–316.

4. Клейн Г.К. Руководство к практическим занятиям по курсу строи-

тельной механики. Статика стержневых систем: Учеб. пособие /

Г.К. Клейн, Н.Н. Леонтьев. – М.: Высш. школа, 1980. – 384 с.

Гл. IX. Расчёт рам методом сил. § IX.1. Порядок расчёта рам. –

С. 137.

5. Анохин Н.Н. Строительная механика в примерах и задачах.

Ч. 1.

Статически определимые системы: Учеб. пособие /

Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 1999. –

334 с.

Гл. 1. Кинематический анализ расчётных схем. § 1.2. Определение

степени статической неопределимости плоских стержневых систем

и образование из них статически определимых путём удаления

лишних связей. – С. 22–28.

49 50

ЛЕКЦИЯ ПЯТНАДЦАТАЯ

ТЕОРЕМЫ ВЗАИМНОСТИ СТРОИТЕЛЬНОЙ МЕХАНИКИ

15.1. Теорема о взаимности возможных работ

15.2. Теорема о взаимности перемещений

15.3. Теорема о взаимности реакций

15.4. Теорема о взаимности реакций и перемещений

15.5. Вопросы для самопроверки

15.6. Рекомендуемая литература

15.1. Теорема о взаимности возможных работ

Рассмотрим два состояния какого-либо сооружения, напри-

мер балки на двух опорах (

рис. 15.1,а). В состоянии i на эту балку

действует обобщённая сила F

, а состоянии j – обобщённая сила

. Обобщённые силы F

и F

в упомянутых состояниях приклады-

ваются статическим способом. На рис. 15.1,а показаны действи-

тельные (Δ

, Δ

) и возможные (Δ

, Δ

) перемещения по направле-

нию обобщённых сил (о статическом способе приложения на-

грузки и о смысле понятий "действительное перемещение", "воз-

можное перемещение" см. в п. 10.2 десятой лекции второй части

"Лекций по строительной механике стержневых систем").

Вычислим работу обобщённых сил F

и F

от их совместного

воздействия. Сначала статическим способом приложим обоб-

щённую силу F

, которая на перемещении Δ

будет совершать

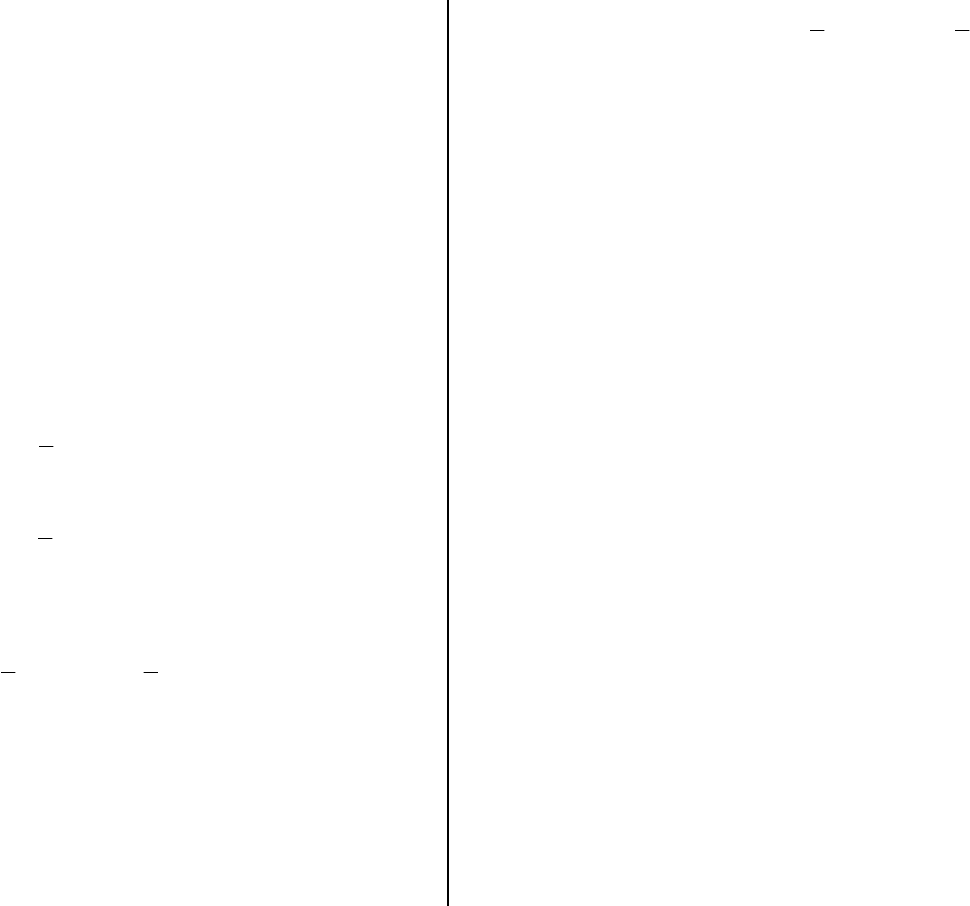
51 52

действительную работу W

ext,ii

(рис. 15.1,б). После окончательного

формирования обобщённой силы F

статическим способом при-

ложим обобщённую силу F

. Балка получит дополнительные де-

формации и перемещения: Δ

– возможное перемещение в на-

правлении обобщённой силы F

от действия обобщённой силы F

– действительное перемещение в направлении обобщённой

силы F

от её же воздействия (рис. 15.1,б внизу). Постоянная по

величине обобщённая сила F

совершает возможную работу W

ext,ij

на перемещении Δ

, а статически приложенная сила F

– действи-

тельную работу W

ext,jj

на перемещении Δ

. Суммарная работа

)1(

ext

W внешних обобщённых сил будет равна

jj,extij,extii,ext

)1(

ext

WWWW ++= .

В п. 10.2 десятой лекции получены зависимости для вычис-

ления действительной и возможной работы внешних обобщён-

ных сил F

и F

iiiii,ext

W Δ= ,

ijiij,ext

FW Δ= ,

jjjjj,ext

W Δ=

Таким образом, выражение суммарной работы от совместно-

го действия обобщённых сил F

и F

в случае, когда первой при-

кладывается сила F

, а второй F

, примет вид:

jjjijiiii

)1(

ext

W Δ+Δ+Δ= . (15.1)

Рассмотрим обратный порядок приложения обобщённых

сил: первой приложим статическим способом обобщённую силу

, а затем, после её окончательного формирования, – обобщён-

ную силу F

(рис. 15.1,в). Суммарная работа внешних обобщён-

ных сил F

и F

)2(

ext

W в этом случае запишется:

ii,extji,extjj,ext

)2(

ext

WWWW ++= .

Учитывая, что W

ext,ji

= F

, получим:

iiijijjjj

)2(

ext

W Δ+Δ+Δ= . (15.2)

Значение суммарной работы внешних обобщённых сил F

не зависит от последовательности их приложения, т.е.

)1(

ext

W =

)2(

ext

Приняв во внимание соотношения (15.1) и (15.2) оконча-

тельно будем иметь:

= F

, или

ext,ij

= W

ext,ji

. (15.3)

Выражение (15.3) и составляет содержание теоремы о взаим-

ности возможных работ внешних сил: возможная работа i-й

обобщённой силы (внешних сил i-го состояния) на перемещени-

ях, вызванных j-й обобщённой силой (внешними силами j-го со-

стояния), равна возможной работе j-й обобщённой силы (внеш-

них сил j-го состояния) на перемещениях, вызванных i-й обоб-

щённой

силой (внешними силами i-го состояния). В строитель-

ной механике эта теорема носит имя итальянского учёного Энри-

ко Бетти (1823–1892).

Без доказательства отметим справедливость теоремы Бетти

для внутренних сил

int,ij

= W

int,ji

т.е. возможная работа внутренних сил i-го состояния на деформа-

циях j-го состояния равна возможной работе внутренних сил j-го

состояния на деформациях i-го состояния.

Из теоремы Бетти, как частный случай, вытекают другие

теоремы взаимности строительной механики, широко используе-

мые в расчётах сооружений.

15.2. Теорема о взаимности перемещений

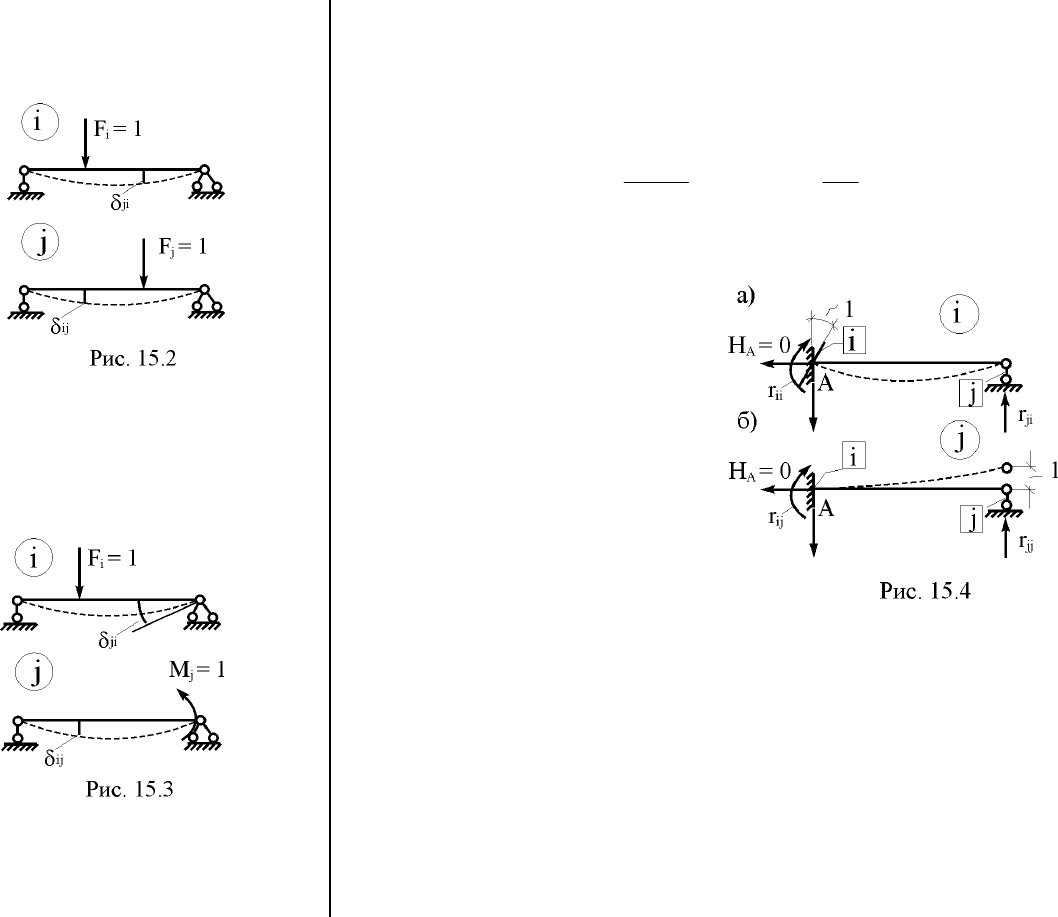
По-прежнему рассмотрим состояния i и j одного и того же

сооружения (рис. 15.2). В состоянии i на него действует сила

= 1, а в состоянии j – сила F

= 1. Зафиксируем возможные пе-

ремещения δ

и δ

, возникающие в состояниях i и j от единичных

сил.

53 54

Для состояний сооружения i и j применим теорему о взаим-

ности возможных работ внешних сил (см. п. 15.1, соотношение

(15.3)):

1 ⋅ δ

= 1 ⋅ δ

, или δ

= δ

. (15.4)

Соотношение (15.4) выражает со-

держание теоремы о взаимности пере-

мещений: перемещение по направлению

линии действия i-й единичной обобщён-

ной силы, вызванное j-й единичной

обобщённой силой, равно перемещению

по направлению линии действия j-й

обобщённой силы от i-й единичной

обобщённой силы. В строительной ме-

ханике эта теорема известна как теорема

английского физика и

механика Джейм-

са Максвелла (1831–1879).

Теорема о взаимности перемещений широко применяется в

расчётах линейно деформируемых систем, в частности, в расчё-

тах статически неопределимых систем методом сил, при по-

строении линий влияния перемещений в стержневых соору-

жениях.

Выше был рассмотрен случай, ко-

гда в состоянии i и j сооружения дейст-

вуют единичные сосредоточенные силы

(

рис. 15.2), т.е. силы, имеющие одина-

ковую природу и одинаковую размер-

ность. На рис. 15.3 рассмотрена ситуа-

ция, когда в состоянии i на сооружение

действует сосредоточенная сила F

= 1,

а состоянии j – сосредоточенный мо-

мент M

= 1. Здесь же показаны и воз-

можные перемещения δ

и δ

, вызывае-

мые упомянутыми силами F

= 1 и M

= 1. Кажущееся противоре-

чие в размерностях перемещений δ

и δ

, равенство которых оп-

ределено соотношением (15.4), отпадает, если мы примем во

внимание, что каждое из этих перемещений является удельным

перемещением, т.е. что оно вызывается обобщённой силой,

имеющей не произвольное, а единичное значение. Таким обра-

зом, размерность какого-либо удельного перемещения есть от-

ношение размерности рассматриваемого обобщённого переме-

щения к размерности

обобщённой силы, вызвавшей это переме-

щение. В случае, рассмотренном на рис. 15.3, имеем:

[δ

] =

смкН

см

⋅

= кН

-1

, [δ

] =

кН

рад

= кН

-1

т.е. оба перемещения имеют одинаковую размерность.

15.3. Теорема о взаимности реакций

Задана любая статиче-

ски неопределимая стержне-

вая система, например, од-

нопролётная балка, защем-

лённая на левом конце и

шарнирно опёртая на пра-

вом. В состоянии i этой бал-

ки угловой связи i заделки А

зададим поворот по часовой

стрелке на единицу

(рис. 15.4,а), а в состоянии j

– правой опорной связи j ли-

нейное перемещение

вверх

на единицу (рис. 15.4,б). Так как рассматриваемая система стати-

чески неопределима, то в её опорных связях, за исключением го-

ризонтальной связи левой опоры А, от упомянутых выше кине-

матических воздействий возникнут реакции (см. п. 14.1 четырна-

дцатой лекции). Горизонтальная связь левой опоры А является

абсолютно необходимой и в ней реакция

от рассматриваемых

смещений связей i и j будет равна нулю (Н

= 0).

На рис. 15.4 в состояниях i и j показаны реакции в смещае-

мых связях, а именно: r

– реакция в i-й связи от её смещения на

единицу, r

– реакция в j-й связи от собственного смещения на

единицу, r

– реакция в i-й угловой связи от перемещения j-й ли-

нейной связи на единицу, r

– реакция в j-й линейной связи от пе-

55 56

ремещения i-й угловой связи на единицу. К состояниям i и j при-

меним теорему о взаимности возможных работ внешних сил (см.

соотношение (15.3) п. 15.1):

ext,ij

= W

ext,ji

В нашем случае:

ext,ij

= r

⋅ 0 + r

⋅ 1, W

ext,ji

= r

⋅ 0 + r

⋅ 1,

⋅ 1 = r

⋅ 1, или r

= r

. (15.5)

Работа реакций остальных связей заданного сооружения (на

рис. 15.4 – реакция вертикальной связи левой опоры А), не полу-

чивших перемещений, в выражения для возможных работ W

ext,ij

ext,ji

не войдёт.

Равенство (15.5) является математическим представлением

теоремы о взаимности реакций: реакция r

в i-й связи от переме-

щения j-й связи на единицу равна реакции r

в j-й связи от сме-

щения j-й связи на единицу.

Принцип взаимности реакций, вытекающей из теоремы Бет-

ти как частный случай, справедлив не только для реакций опор-

ных связей различного типа, но и для реакций внутренних связей

(изгибающих моментов, поперечных и продольных сил).

Как и в теореме о взаимности перемещений

(см. п. 15.2), в

рассматриваемой здесь теореме о взаимности реакций речь идёт

об удельных реакциях, т.е. реакциях, вызванных единичными

смещениями связей. Размерность удельной реакции определяется

как отношение размерности рассматриваемой реакции к размер-

ности перемещения, вызвавшего эту реакцию. Для удельных ре-

акций r

и r

, показанных на рис. 15.4, имеем:

] =

см

смкН ⋅

= кН, [r

] =

рад

кН

= кН.

В строительной механике теорема о взаимности реакций из-

вестна как первая теорема английского физика Джона Рэлея

(1842–1919). Она широко применяется в расчётах статически не-

определимых систем методом перемещений.

15.4. Теорема о взаимности реакций и перемещений

На рис. 15.5 показаны два состояния произвольной статиче-

ски неопределимой системы (рамы). В первом состоянии (со-

стоянии i) на раму действует обобщённая сила F

= 1. Опорная

связь j получает единичное перемещение во втором состоянии

(состоянии j). Введём обозначения: r'

– реакция в j-й связи от

обобщённой силы F

= 1 в состоянии i, δ'

– перемещение по на-

правлению обобщённой силы F

= 1 от смещения связи j на еди-

ницу в состоянии j. За положительное направление перемещения

δ'

примем перемещение, происходящее по направлению обоб-

щённой силы F

= 1, а за положительную реакцию r'

реакцию,

направление которой совпадает с перемещением j-й связи.

Для состояний i и j используем теорему о взаимности воз-

можных работ внешних сил (см. соотношение (15.3) в п. 15.1).

ext,ij

= 1 ⋅ δ'

+ r'

⋅ 1.

Возможная работа W

ext,ji

внешних сил состояния j на пере-

мещениях, вызываемых внешними силами состояния i, равна ну-

лю, так как в состоянии i перемещения по направлению опорных

связей в том числе и по направлению связи j, отсутствуют, т.е.

ext,ji

= 0.

В соответствии с выражением (15.3) W

ext,ij

= W

ext,ji

, поэтому

⋅ δ'

+ r'

⋅ 1 = 0, или r'

= –δ'

. (15.6)

Соотношение (15.6) является математической формулиров-

кой теоремы о взаимности реакций и перемещений: реакция в j-й

связи сооружения от обобщённой силы F

= 1 с обратным знаком