Ковалюк Д.О., Москвіна С.М. Моделювання теплотехнологічних об’єктів з розподіленими параметрами
Подождите немного. Документ загружается.


30
Як один із різновидів аналітичних методів хочеться виділити пі-
дхід, запропонований в роботах Бутковського [17–19], який аналогіч-
но до теорії автоматичного управління передбачає структурне пред-
ставлення системи у вигляді елементарних розподілених блоків. Під
елементарним розподіленим блоком тут розуміється блок, імпульсна
перехідна функція якого є розв’язком деякої елементарної задачі рів-
нянь математичної фізики.
Цей підхід може бути використаний у випадку, коли для даного
класу теплотехнологічних об’єктів от
римані математичні моделі з ви-
значеним
и вхідними та вихідними співвідношеннями, що пов’язують
вхідні впливи з відповідною реакцією об’єктів. Основними етапами
цього підходу є:
структурне представлення теплотехнологічних ОРП та їх
опис в термінах передатних функцій;
розрахунок базових характеристик ОРП;
Зазначимо, що для дослідження моделей теплотехнологічних
ОРП використовуються методи операційного числення та кінцеві ін-
тегральні перетворення. Проте, як стверджується в [118], навіть у най-
більш простих ситуаціях, що допускають представлення ОРП у формі
“елементарних” лінійних розподілених блоків з відомими співвідно-
шеннями вхід-вихід, системи з розподіленими параметрами опису-
ються точними математичними моделями досить складного виду. А в
більш складних випадках, наприклад, для просторових багатовимір-
них об’єктів зі складною формою границі області зміни просторових
координат або при необхідності враховувати істотні нелінійні ефекти,
як правило, взагалі не вдається одержати аналітичний розв’язок рів-
нянь об’єкта.
З огляду на вказані труднощі в роботах [74, 78, 82, 108, 128] роз-
глядаються методи, що базується на принципі використання наближе-
них моделей ОРП.
Наближені методи можна умовно поділити на дві частини, пер-
ша з яких в базується на перетворенні математичної моделі ТОРП до
спрощеного вигляду та знаходженні її розв’язків. Ці розв’язки будуть
наближеними розв’язками вихідної задачі. Друга частина методів пе-
редбачає перегляд суті розподіленого об’єкта і отримання мат
ематич-
31
них моделей, які описують функціонування його частин (зон), з пода-
льшим знаходженням їх параметрів.
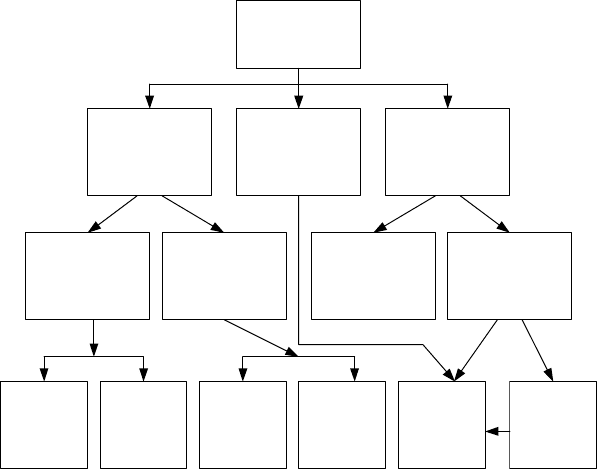
На наш погляд, найбільш вдалою є класифікація наближених
методів перетворення моделей ОРП, запропонована в роботах Рапо-
порта [117, 118]. Розглянемо її більш детально (рис. 1.4).
Згідно з цією класифікацією методи наближеного моделювання
теплотехнологічних ОРП можуть бути умовно поділені на дві основ
ні
групи за “предметом апрок
симації”. Перша група основана на спро-
щеному поданні самих вихідних диференціальних рівнянь об’єкта,
подальший розв’язок яких відомими методами дозволяє одержати за-
довільні за точністю описи властивостей ОРП у порівняно простому
вигляді.
Наближені методи
моделювання ОРП
Методи
кінцевомірних
наближень
Методи переходу
до розподілених
блоків спрощеної
структури
Методи
апроксимації
наближених
розв'язків об'єкта
Експериментальні
методи
Методи
апроксимації
вихідних рівнянь
об'єкта
Методи
розкладання
передаточних
функцій в
нескінчені ряди
Методи визна-
чення параметрів
передаточних
функцій заданої
структури
Різницеві
меоди
Методи
парамет-
ричної
ідентифіка-
ції
Аналітичні
методи
Методи
модально-
го опису
об'єкта
Методи
лінеари-
зації
Методи
малого
параметра
Рис. 1.4. Класифікація методів наближеного моделювання ОРП
Методи другої групи базуються на наближеному поданні (як
правило, у типовій для ОЗП формі відповідних передатних функцій)
точних розв’язків рівнянь в частинних похідних, що моделюють фун-

32
кціонування ОРП. Зазначимо, що послідовне застосування до того ж
самого ОРП різних методів апроксимації, дозволяє спочатку перейти
до спрощеного рівняння об’єкта, що допускає точний аналітичний
розв’язок, а потім знайти дрібно-раціональне наближення його пере-
датної функції, що визначає підсумковий наближений опис вихідної
моделі об'єкта в рамках типових моделей ОЗП.
Методи апроксимації вихідних рівнянь об’єкта. Способи на-
ближеного опису ОРП, пов’язані зі спрощенням самих рівнянь
об’єкта, можуть бути реалізовані шляхом переходу до більш простих
рівнянь у частинних похідних, що зберігає просторово-часовий харак-
тер функції стану об’єкта і по можливості допускає точний аналітич-
ний розв’язок, або безпосереднім перетворенням до скінченовимірної
системи шляхом використання процедури дискретизації.
З методів редукції до спрощених рівнянь в частинних похідних
відзначимо насамперед методи лінеаризації і малого параметра [78,
83, 118, 167], а з скінченовимірних наближень – опис на базі модаль-
ного представлення об’єкта і різницеві моделі. Методи переходу до
спрощених розподілених блоків [19, 117] дозволяють зберегти при їх-
ньому коректному використанні всі основні якісні особливості дослі-
джуваних ОРП в розглянутих умовах, що є їх вагомою перевагою.
Методи скінченовимірної апроксимації, які розглядаються в ро-
ботах [32, 59, 75, 81, 85, 86, 119, 125], пов’язані з переходом до класу
моделей зовсім іншої природи в порівнянні з вихідними об’єктами, що
породжує істотні особливості цього способу моделювання ОРП. Без-
сумнівною перевагою такого підходу є його універсальність, що до-
зволяє одержати наближений опис навіть досить складних ОРП в ана-
літичній або цифровій формі за допомогою сучасних методів обчис-
лювальної математики.
Методи апроксимації точних розв’язків рівнянь об’єкта. Як за-
значено в [20, 33, 118], широкого застосування в інженерній практиці
набули різні методи наближеного моделювання передатних функцій
ОРП, що представляються в типовій для систем із зосередженими па-
раметрами дрібно-раціональній формі, яка іноді доповнюється ланка-
ми чистого запізнення.

33
Зокрема, широко використовуються розкладання точних виразів
для передатних функцій або їх окремих складових різними способами
в нескінченні збіжні ряди, що дозволяють, знайти таке дрібно-
раціональне представлення з будь-якою необхідною точністю перші
члени ряду, що утворять у сукупності типові динамічні ланки ОЗП
першого, другого або третього порядку. Передатні функції можуть бу-
ти при цьому попередньо знайдені у формі нескінченного ряду, на-
приклад, при використанні методу кінцевих інтегральних перетворень
або представлені їх розкладаннями в ряди Тейлора, а також і в ряди по
відображенням різних ортогональних функцій.
Широко застосовується й інший метод апроксимації [117, 119],
при якому, базуючись на фізичних представленнях експерименталь-
них даних, досвіді роботи з аналогічними об’єктами, грубих аналітич-
них описах і т. д., апроксимують передатні функції з точністю до зна-
чень коефіцієнтів у типовий для ОЗП формі, конкретний вигляд якої
диктується зазначеними міркуваннями. В такому випадку задача зво-
диться до вибору цих коефіцієнтів з умов мінімізації помилки набли-
ження. Тут також можуть застосовуватися різні обчислювальні алго-
ритми, що приводять до наближених виразів для ПФ із коефіцієнтами,
параметрично залежними від просторових змінних.
Експериментальні методи. Частина методів наближеного моде-
лювання основана на апроксимації розподіленої системи та передба-
чає перегляд суті розподіленого об’єкта і отримання математичних
моделей його частин В цьому випадку здійснюється розбиття просто-
рової області, на достатнє кінцеве число невеликих областей і усеред-
нені розподілених параметрів всередині кожної такої області. Таким
чином з ряду зосереджених підсистем отримується деяка взає-
мозв’язан
а си
стема. При такому переході широко використовуються
розроблені стосовно ОЗП методи ідентифікації [89, 92, 145], безпере-
чною перевагою яких є можливість одержання наближеної моделі в
умовах, коли складний характер об'єкта і (або) відсутність достатньо-
го обсягу інформації про вихідні дані ускл
аднюють опис моделі аналі-
тичним шляхом. До очевидних недоліків методів ідентифікації
по ек-
спериментальним даним відноситься, насамперед, частковий характер
одержуваних результатів, правомірних лише стосовно до конкретних
34
режимів роботи конкретного об'єкта з конкретними значеннями від-
повідних параметрів [106, 108]. Крім того кінцеві наближення можуть
привести до втрати сутнісних властивостей, обумовлених просторо-
вою розподіленістю керованих процесів. При використанні кінцевих
моделей можуть виявитися “непоміченими” властивості некерованості
об'єкта, що означають, зокрема, неможливість здійснити його перехід
у необхідний кінцевий стан із заданого початкового в заданому класі
керуючих впливів; властиво
сті обмеженості в
часі такого переходу;
властивості неможливості реалізації оптимальних за рядом критеріїв
алгоритмів керування; неправомірність застосування в ряді випадків
апарата теорії керування зосередженими системами та ін.
Серед наближених методів розв’язання диференційних рівнянь в
частинних похідних значне місце займають варіаційні методи [11, 86,
125]. Це пояснюється тим, що багато законів механіки та фізики зво-
дяться до твердження про досягнення мінімуму чи мак
симуму функ-
ціоналом, який
характеризує відповідний процес. До числа таких варі-
аційних принципів або їх простих наслідків належать: принцип най-
меншої дії, закон збереження енергії, закон збереження імпульсу,
принципи теорії поля, тощо.
Основна задача варіаційного числен
ня формулюється наступ-
ним чином. В деякій області G простору дійсних змінних
12
,,,...,
n
x
yy y
для довільних кінцевих дійсних значень
12
, ,...,
n
zz z
за-
дана неперервна по сукупності всіх своїх аргументів дійсна функція:
12 12
( , , ,..., , , ,..., ) ( , , )
nn
f
xy y y z z z f xYZ
=
, (1.44)
де
12
, ,...,
n
Yyy y=
,
12
, ,...,
n
Z
zz z=
.
Розглядається сукупність
Ω
всіх кусочно-гладких просторових
кривих,
()YYx=
, що лежать в області G і з’єднують дві задані точки
12
(, ,..., )(,)
n
aa a aA=
і
12
(, ,..., ) (,)
n
bb b bB
=
. На кожній такій допустимій
кривій інтеграл
(, , )
b
a
f
xYY dx
′
∫
(1.45)
має визначене значення. Шукається та крива або криві, на яких даний
інтеграл має екстремальне значення. Таким чином, варіаційне числен-

35
ня вивчає методи, що дозволяють знаходити максимальні і мінімальні
значення функціоналів.
Розглядаючи застосування варіаційного числення до розв’язання
диференційних рівнянь в частинних похідних, зауважимо, що в основі
даних методів лежить заміна крайової задачі для диференційного рів-
няння еквівалентною їй варіаційною задачею. Наближене розв’язання
крайової задачі зводиться до отримання наближеного розв’язку ві
дпо-
відної варіаційної задачі. Наглядним прик
ладом цього є метод скінче-
них елементів, в якому фізична задача замінюється кусково-гладкою
моделлю.
1.4.2. Чисельні методи
В значній частині випадків для отримання розв’язків моделей
теплотехнологічних ОРП використовуються чисельні методи
розв’язання системи диференціальних рівнянь в частинних похідних,
яка описує функціонування таких об’єктів. Тому доцільно приділити
увагу найбільш поширеному з них – методу кінцевих різниць.
Алгоритми розв’язання задач за допомогою, кінцево-різницевих
методів, як правило, є поєднанням методів побудови різницевих ана-
логів задач та методів їх розв’язання.
Оскільки різницеві методи моделювання є найбільш розповсю-
дженими [55, 75, 86], то розглянемо загальну схему їх функціонування
на прикладі типової моделі ОРП, яка описується просторово однови-
мірним рівнянням другого порядку
22
1
22
11
(,) (,) (,)
()
(,)
() (,) (,,(,))
Qxt Qxt Qxt
AACx
t
tx
Qxt
B
CxQxt fxtuxt
x
∂∂ ∂
+=
∂
∂∂
∂
++ +
∂
(1.46)
при початкових і граничних умовах:
(0) (1)
0001
(,0)
(,0) (), (),
Qx
Qx Q x Q x x x x
t
∂
==≤≤
∂
; (1.47)
0
00 0 00
(,)
( , ) ( , ( )), 0
Qx t
Qx t g tu t t
x
∂
α+β = >
∂
; (1.48)
1
11 1 11
(,)
( , ) ( , ( )), 0.
Qxt
Qxt g tu t t
x
∂
α+β = >
∂
(1.49)
36
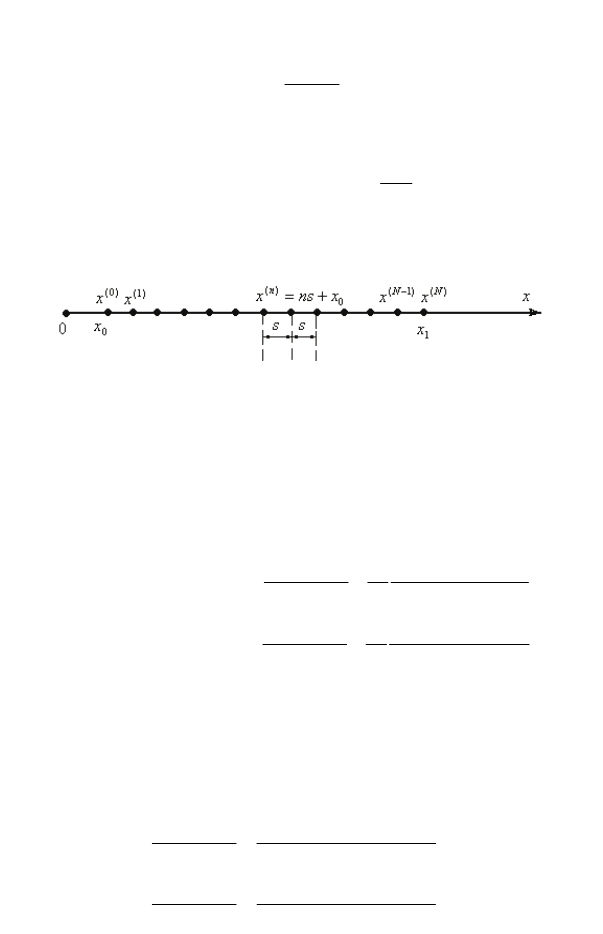
Виконуючи дискретизацію по просторовій змінній
x
, розіб’ємо
відрізок її зміни [
0
x
,
1
x
] на N рівних інтервалів при
10
x
x
s
N
−
=
(1.50)
точками
(0) (1) (2) ( )
00 0
, , 2 , ..., ;
n
x
xx sxx sx x==+=+
(1.51)
()
0
,0,
n
x
ns x n N=+ =
, (1.52)
які утворюють рівномірну просторову сітку з кроком
s
(рис. 1.5):
Рис. 1.5. Просторова сітка для одновимірних моделей ОРП
Використовуючи розкладання функції стану об’єкта
(,)Qxt
у
ряд Тейлора по змінній
x
у точці
(
)
n
x
у вигляді, що містить додатко-
вий член у формі Лагранжа, отримаємо для значень відповідної сітко-
вої функції в точках
(
)
1n
x
+
,
(
)
1n
x
−
:
() 2 2 ()
(1) ()
1
2
(,) ( ,)
(,)(,) ,
2
nn
nn
Qx t s Qx s t
Qx t Qx t s
x
x
+
∂∂+η
=+ +
∂
∂
(1.53)
() 2 2 ()
(1) ()
2
2
(,) ( ,)
(,)(,) ,
2
nn
nn
Qx t s Qx s t
Qx t Qx t s
x
x
−
∂∂−η
=− +
∂
∂
(1.54)
де η
1
, η
2
– деякі числа, такі, що 0≤η
1
≤1; 0≤η
2
≤1.
Нехтуючи при досить малому s членами з s
2
, знайдемо відповід-
ні наближені вирази для обчислення перших похідних через різниці
самої функції:
() ( 1) ()
(,) ( ,)(,)
;
nn n
Qx t Qx t Qx t
xs
+
∂−
≅
∂
(1.55)
() () ( 1)
(,) (,)( ,)
.
nnn
Qx t Qx t Qx t
xs
−
∂−
≅
∂
(1.56)
37
Похибки Е такого представлення визначаються знехтуваними
членами розкладу (1.53) і (1.54) і оцінюються співвідношеннями:
2
2
(,)
max ,
2
s
Qxt
E
x
∂
≤
∂
(1.57)
2
2
(,)
max ,
2
s
Qxt
E
x
∂
≤
∂
(1.58)
для правих і лівих різницевих похідних відповідно.
Якщо дискретизація здійснюється не тільки по просторовій, але
і по часовій змінній, з наступним використанням різницевих аналогів,
подібних (1.55), (1.56), для всіх частинних похідних функції стану
об’єкта, то в підсумку отримують кінцево-різницеві апроксимації вихі-
дної моделі вже у формі системи алгебраїчних рівнянь щодо значень
цієї функції на просторово-часовій сітці. До подібного вигляду зво-
дяться і диференціально-різницеві описи при різницевому представ-
ленні похідних за часом з метою чисельного розв’язку відповідних за-
дач Коші.
Нехай, зокрема, поряд з (1.51) вводиться рівномірне квантуван-
ня тимчасової змінної на інтервалі [0, T]:
1
()
(0) (1) (2)
1
0, , 2 ,..., ; ,
N
T
tththtTh
N
== = ==
(1.59)
де
1
N
– задане число.
Таким чином, утворюється просторово-часова сітка на прямоку-
тнику
01
[][0]
x
xx tT≤≤ × ≤≤
зміни аргументів функції
(,)Qxt
пока-
зана на рисунку 1.6:
() ( )
01
,0,; , 0,.
nm
x
ns x n N t mhm N=⋅+ = = ⋅ =
(1.60)
В залежності від вибору комбінації вузлів сітки (1.60), яка вико-
ристовується для різницевого представлення похідних, можливі різні
схеми кінцево-різницевої апроксимації.
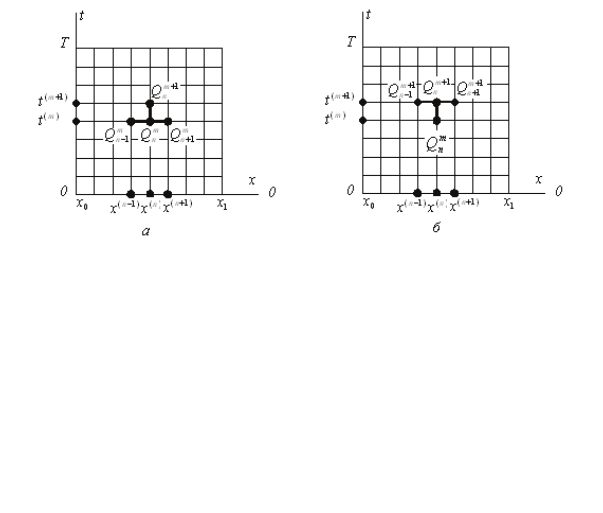
38
Рис. 1.6. Сіткові шаблони для кінцево-різницевої апроксимації
одновимірного рівняння теплопровідності за явною (а) і неявною (б)
схемами
Проте для даного підходу також присутні недоліки, пов’язані з
обґрунтуванням збіжності, стійкості чисельних методів і оцінкою по-
хибки. Крім того, при використанні методів численного розв’язку
отриманий результат через складність обчислень (великі затрати часу
та комп’ютерної пам’яті) важко використовувати для синтезу оптима-
льного управління в реальному часі.
1.4.3. Інтелектуальні методи
Для багатьох ТП має велике значення не лише управління по ві-
дхиленню параметрів, але й рекомендації щодо запобігання та усу-
нення цього відхилення. Тому на перше місце виходять поняття адап-
тивних та інтелектуальних систем, які дозволяють не тільки розрахо-
вувати параметри управління для мінімізації відхилення, але й моде-
лювати на декілька кроків вп
еред та прогнозу
вати стан технологічно-
го процесу.
Математичним апаратом для побудови таких систем є інтелек-
туальні технології, найбільш поширеними з яких на сьогодні стали
нечітка логіка [1, 120, 143, 160, 161] та нейронні мережі [43, 87, 156,
164].
Досвід створення систем автоматичного управління для склад-
них технологічних об’єктів в умовах невизначеності та неповноти ін-
формації про об’єкт засвідчи
в нееф
ективність застосування лише фо-
39
рмальних класичних методів теорії управління. Останнім часом спо-
стерігається високий інтерес до одного з найважливіших застосувань
теорії нечітких множин – аналізу та синтезу нечітких регуляторів та
систем управління технологічними процесами [4, 13, 45, 68, 88]. Ве-
лику кількість практичного застосування нечітких систем управління
в промисловості, транспорті, побутових приладах відмічено в Японії,
Китаї, США, європейських країнах [169, 172, 175-177].
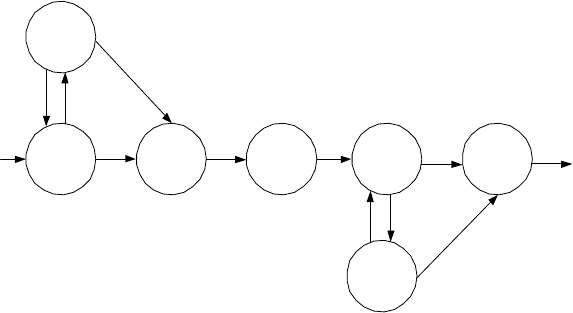
Як приклад розглянемо систему управління, запропоновану в
робот
і [158], що включає нечіткий
гібридний контролер для управлін-
ня тепловим процесом, показаний на рис. 1.7.
Цей контролер, використовуючи значення температури, іденти-
фікує стан температурної кривої та виконує відповідне перемикання
виконавчих механізмів.
1
FC
6
FC
5
FC
4
FC
3
FC
2
FC
0
FC
20
0
<e
20
0
>e
1
^1200 ttx
=
=
40
0
<
e40
0
>e
2
^1500 ttx
=
=
3
tt
=
4
^
1200
tt
x
=
=
Рис. 1.7. Граф перемикання температурної кривої
Узагальнена схема інтелектуальної системи управління на осно-
ві нейромережі показана на рис. 1.8. В цьому випадку нейромережа
використовується як засіб прогнозування виходу об’єкта управління
()
p
yt
при певних значеннях управляючих впливів
()ut
. Використання
моделі прогнозування дозволяє знаходити параметри управління для
отримання потрібного значення
()yt
.
