Kounadis A.N., Gdoutos E.E. (Eds.) Recent Advances in Mechanics

Подождите немного. Документ загружается.

Experimental Mechanics in Nano-engineering 279

where: E(x, τ) is the scalar representation of the propagating electromagnetic

field, x is the direction of propagation of the field, τ is the time, A(k) is the

amplitude of the field, k is the wave number 2π/λ, ω(k ) is the angular frequency.

A(k) provides the linear superposition of the different waves that propagate and

can be expressed as:

A(k) π2= δ(k-k

) (6)

where δ(k-k

) is the Dirac’s delta function. This amplitude corresponds to a

monochromatic wave, that is: E(x,τ)=

τω )k(i

ikx

e . If one considers a spatial pulse

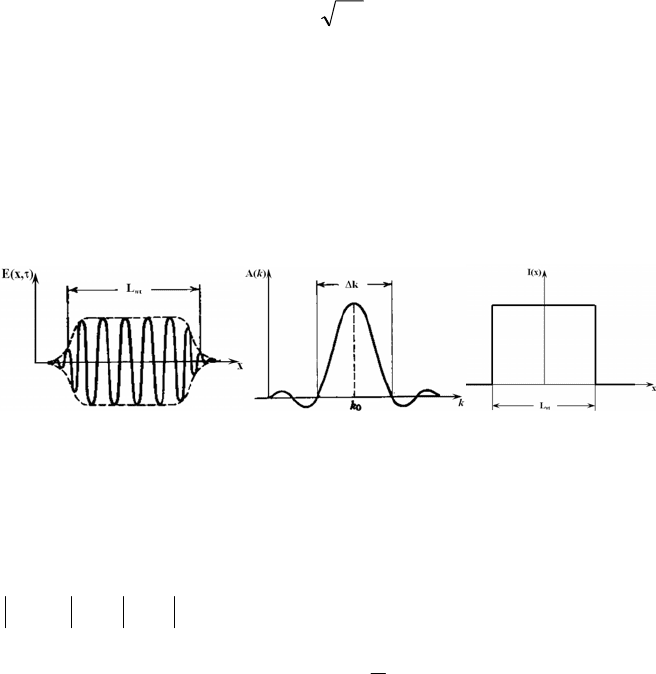
of finite length (see Fig. 2a), at the time τ=0, Ε(x,0) represents (see Fig. 2c) a

finite wave-train of length L

where A(k) is not a delta function but a function

that spreads a certain length Δk (Fig. 2b). The dimension of L

depends on the

analyzed object size. In the present case, objects are smaller than the wavelength

of the light.

a) b) c)

Fig. 2. a) Harmonic wave train of finite extent L

; b) Corresponding Fourier spectrum in

wave numbers k; c) Representation of a spatial pulse of light whose amplitude is described

by the rect(x) function.

In Ref. [9], it is stated that if L

and Δk are defined as the RMS deviations

from the average values of L

and Δk evaluated in terms of the intensities

)0,x(E and

)k(A , then it follows:

≥Δ (7)

Since L

is very small, the spread of wave numbers of monochromatic waves

must be large. Hence there is a quite different scenario with respect to the classical

context in which the length L

is large when compared to the wavelength of light.

In order to simplify the notation, one can reason in one dimension without loss

of generality. The spatial pulse of light represented in Fig. 2c is defined as

follows:

)x(rectA)x(A

= (8)

280 C.A. Sciammarella, F.M. Sciammarella, and L. Lamberti

where:

⎪

⎩

⎪

⎨

⎧

elsewhere0

|x|

|x|1

)x(rect

(9)

The Fourier transform of A(x) is equal to sinc(x). The Fourier transform of

the light intensity [A(x)]

is hence [sinc(x)]

. To the order 0 it is necessary to add

the shifted orders ±1. The function A(x±Δx) can be represented through the

convolution relationship:

'dx)xx()'x(A)xx(A ⋅Δ±δ⋅=Δ±

∫

+∞

∞−

(10)

where x’=x±Δx. The Fourier transform of the function A(x ±Δx) will be:

x)]2/x(f2[i

e)f(A)]xx(A[FT

 'r

(11)

where f

is the spatial frequency. The real part of Eq. (11) is:

^`^ `

x)]2/x(f2[osc)f(A]xx(A[FTRe

'S 'r #

(12)

By taking the Fourier transform of Eq. (12), one can return back to Eq. (10).

For the sake of simplicity, the above derivations have been done in one

dimension but can be extended to 3-D. Brillouin

[10] has shown that for a cubic

crystal the electromagnetic field can be represented as the summation of plane

wave fronts with constant amplitude as it has been assumed in Eq. (5). In such

circumstances the above derivation can be extended to 3-D and can be applied to

the components of the field in the different coordinates.

2 Applications to Nanometrology

The initial approach to the utilization of evanescent field properties was the

creation of near-field techniques. In the near-field techniques, a probe with

dimensions in the nano-range detects the local evanescent field generated in the

vicinity of the objects that are observed. The following alternative approach to the

classical near-field techniques has been utilized in this paper:

a) Using diffraction through the equivalent of a diffraction grating or to

generate directly an ample spectrum of k vectors by means of a diffraction grating;

b) Creating a Fabry-Perot type cavity;

c) Exciting the objects to be observed with the evanescent fields so that the

objects become self-luminous.

Experimental Mechanics in Nano-engineering 281

The light generated in this way has the particular property of propagating through

space and optical instruments without the common diffraction effects experienced

by ordinary wave fronts [1-3].

The self generation of light by small single crystals of sodium chloride has been

utilized to produce the equivalent of Fourier type holograms [11].

2.1 Observation of Nano-crystals and Nano-spheres

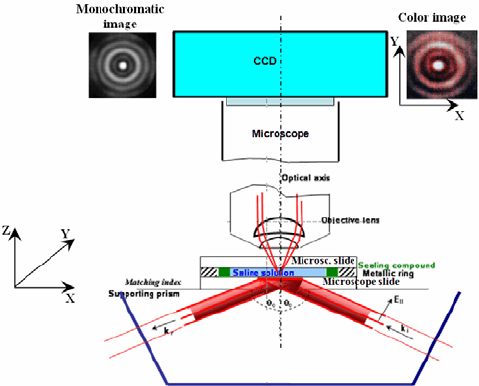
Figure 3 shows the schematic representation of the experimental setup. Following

the classical arrangement of TIR, a helium-neon (He-Ne) laser beam with nominal

wavelength 632.8 nm impinges normally to the face of a prism designed to

produce limit angle illumination on the interface between a microscope slide

(supported by the prism itself) and a saline solution of sodium-chloride contained

in a small cell supported by the slide. Consequently, evanescent light is generated

inside the saline solution.

The objects observed with the optical microscope are supported by the upper

face of the microscope slide. Inside the cell filled with the NaCl solution there is a

polystyrene microsphere of 6 μm diameter. The microsphere is fixed to the face of

the slide through chemical treatment of the contact surface in order to avoid

Brownian motions. The polystyrene sphere acts as a relay lens which collects the

light wave fronts generated by the nano-sized crystals of NaCl resting on the

microscope slide. More details on the polystyrene sphere and the saline solution

properties are given in Table 1.

Fig. 3. Experimental setup to image nano-size objects using evanescent illumination. Two

CCD cameras are attached to a microscope in order to record images: monochromatic,

color.

282 C.A. Sciammarella, F.M. Sciammarella, and L. Lamberti

The observed image is focused by an optical microscope with NA=0.95 and

registered by a monochromatic CCD attached to the microscope. At a second port, a

color camera records color images. The CCD is a square pixel camera with

1600x1152 pixels. The analysis of the image recorded in the experiment has been

performed with the Holo Moiré Strain Analyzer software (HoloStrain™), Ref. [12].

Table 1. Details on polystyrene microsphere and saline solution

Parameter Value Note

Polystyrene microsphere

diameter D

sph

6 ± 0.042 μm

Tolerance specified by the

manufacturer

Polystyrene microsphere

refraction index n

1.57 ± 0.01

Value specified by the

manufacturer

Saline solution

refraction index n

1.36 Computed from NaCl

concentration for the nominal

wavelength of λ=590 nm

2.2 Generation of Multi-k Vector Fields

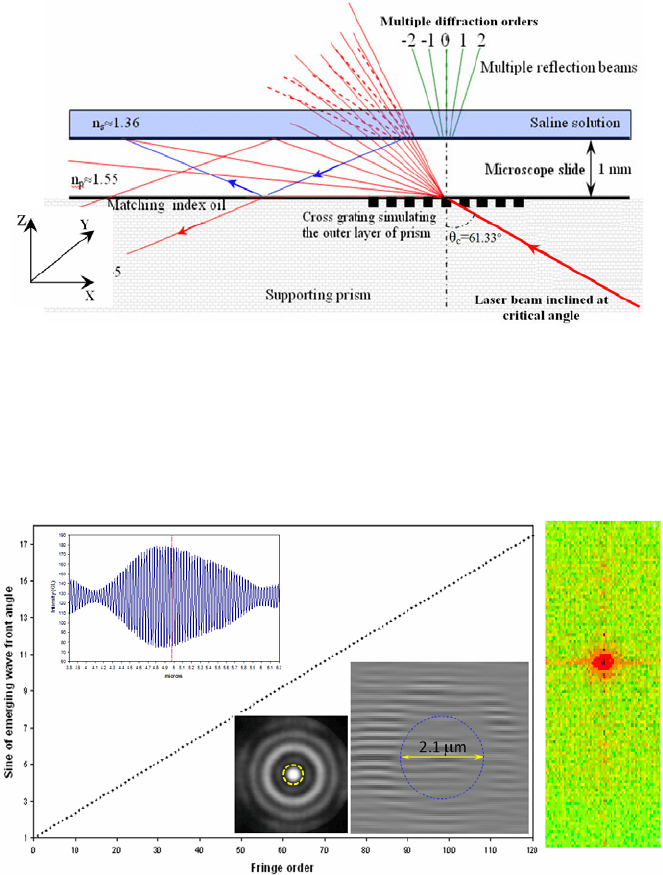
Figure 4 shows the process of generation of the evanescent beams that provide the

energy required for the formation of the images. The optical setup providing the

illumination is similar to the setup originally developed by Toraldo di Francia to

prove the existence of evanescent waves and described in Ref. [6]. A grating is

illuminated by a light beam at the limit angle of incidence θ

. A matching index

layer is interposed between the illuminated surface and a prism which is used for

observing the propagating beams originated on the prism face by the evanescent

waves. In the original experiment conducted by Toraldo di Francia, the diffraction

orders of the grating produced multiple beams that by interference generated the

fringes observed with a telescope. In the present case, the interposed layer

corresponds to the microscope slide. Although the microscope slide does not have

exactly the same index of refraction of the prism, it is close enough to fulfill its

role.

The diffraction effect is produced by the residual stresses developed in the

outer layers of the prism. The multiple illumination beams are the result of

residual stresses in the outer layers of the prism. In Ref. [13], there is a detailed

analysis of the formation of interference fringes originated by evanescent

illumination in presence of residual stresses on glass surfaces. The glass in the

neighborhood of the surface can be treated as a layered medium and the fringe

orders depend on the gradients of the index of refraction. In Ref. [14], there is a

more extensive analysis of the role played by birefringence in the present

example.

Figure 4 provides a schematic representation of the process of illumination of

the observed nano-objects. The laser beam, after entering the prism, impinges on

the prism-microscope slide interface, symbolically represented by a grating, where

it experiences diffraction. The different diffraction orders enter the microscope

slide and continue approximately along the same trajectories determined by the

Experimental Mechanics in Nano-engineering 283

diffraction process. The slight change in trajectory is due to the fact that the

indices of refraction of the prism and the microscope slide are slightly different.

As the different orders reach the interface between the microscope slide and the

saline solution, total reflection takes place and evanescent wave fronts emerge into

the solution in a limited depth that is a function of the wavelength of the light as

shown in Eq. (2).

Fig. 4. Model of the interface between the supporting prism and the microscope slide as a

diffraction grating causing the impinging laser beam to split into different diffraction orders.

Since the wave fronts have been originated by artificial birefringence, for each

order of diffraction there are two wave fronts: the p-polarized and the s-polarized

wave fronts. Upon entering the saline solution these wave fronts originate

propagating wave fronts that produce interference fringes.

Fig. 5. System of fringes observed in the image of the 6 μm diameter polystyrene sphere.

Dotted circle represents the first dark ring in the particle diffraction pattern

284 C.A. Sciammarella, F.M. Sciammarella, and L. Lamberti

Figure 5 shows the diffraction orders corresponding to one family of fringes

that were extracted from the FT of the image captured by the optical system and

contains the diffraction pattern of the microsphere that acts as a relay lens. Since

these wave fronts come from the evanescent wave fronts, their sine is a complex

number taking values greater than 1. Figure 5 includes also the image extracted

from the FT of the central region of the diffraction pattern of the microsphere (the

first dark fringe of the microsphere diffraction pattern is shown in the figure) and

shows the presence of the families of fringes that were mentioned previously. The

fringes form moiré patterns that are modulated in amplitude in correspondence of

the loci of the interference fringes of the microsphere. A total of 120 orders have

been detected for this particular family [15]. These wave fronts play a role in the

observation of the sodium-chloride nano-crystals contained in the saline solution.

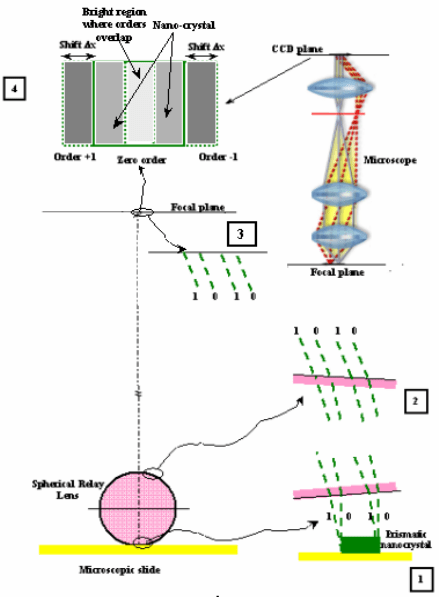
Figure 6 shows the schematic representation of the optical circuit bringing the

images to the CCD detector. The observed patterns are not images in the classical

sense. Therefore, the meaning of the concept of “super-resolution” must be

explained with respect to the present context.

Fig. 6. Schematic representation of the optical system leading to the formation of lens

hologram: 1) Prismatic nano-crystal; 2) Wave fronts entering and emerging from the

polystyrene micro-sphere acting as a relay lens; 3) Wave fronts arriving at the focal plane of

the spherical lens; 4) Wave fronts arriving at the image plane of the CCD. The simulation of

the overlapping of orders 0, +1 and -1 in the image plane of the CCD is also shown.

Experimental Mechanics in Nano-engineering 285

It can be seen that different diffraction orders emerge from the interfaces of the

crystals and the supporting microscope slide. These emerging wave fronts act as

multiplexers creating successive shifted images of the object. Let us assume that

we look at a prism (Fig. 6, Part 1) approximately parallel to the recording CCD

image plane. Successive shifted luminous images of the prism are then recorded.

It is possible to prove that the main energy is concentrated in the zero order and

the first order [11]. These orders overlap in an area that depends on the process of

formation of the image (see Fig. 6). The order 0 produces an image on the image

plane of the optical system, that is centered at a value x of the horizontal

coordinate. Let us call S(x) this image. The order +1 will create a shifted image of

the particle, S(x-Δx). The shift implies a change of the optical path between

corresponding points of the surface. In the present case, the trajectories of the

beams inside the prismatic crystals are straight lines and the resulting phase

changes are proportional to the observed image shifts. Therefore, the phase change

can be written as:

[

]

)xx(S)x(SK)x,x(

Δ=ΔφΔ (13)

where K

is a coefficient of proportionality. Equation (13) corresponds to a shift of

the image of the amount Δx. If the FT of the image is computed numerically, one

can apply the shift theorem of the Fourier transform. For a function f(x) shifted by

the amount Δx, the Fourier spectrum remains the same but the linear term ω

Δx is

added to the phase: ω

is the angular frequency of the FT. It is necessary to

evaluate this phase change. The shift can be measured on the image by

determining the number of pixels representing the displacement between

corresponding points of the image (see Fig. 6, Part 4). Through this analysis and

using the Fourier Transform it is possible to compute the thickness t of the prism

in an alternative way to the procedure that will be described in the following.

These developments are a verification of the mechanism of the formation of the

images as well as of the methods to determine prism thickness [11].

2.3 Formation of Holograms at the Nano-scale

Let us now consider the quasi-monochromatic coherent wave emitted by a nano-

sized prismatic crystal. The actual formation of the image is similar to a typical

lens hologram of a phase object illuminated by a phase grating [16]. The Fourier

Transform of the image of the nano-crystal extended to the complex plane is an

analytical function. If the FT is known in a region, then, by analytic continuation,

F(ω

) can be extended to the entire domain. The resolution obtained in this

process is determined by the frequency ω

captured in the image. The image can

be reconstructed by a combination of phase retrieval and suitable algorithms. The

image can be reconstructed from a F(ω

) such that ω

<ω

sp,max

, where ω

sp,max

determined by the wave fronts captured by the sensor.

The fringes generated by the different diffraction orders experience phase

changes that provide depth information. These fringes are carrier fringes that can

be utilized to extract optical path changes. This type of setup to observe phase

286 C.A. Sciammarella, F.M. Sciammarella, and L. Lamberti

objects was used in phase hologram interferometry as a variant of the original

setup proposed by Burch and Gates[17,18]. When the index of refraction in the

medium is constant, the rays going through the object are straight lines. If a

prismatic object is illuminated with a beam normal to its surface, the optical path

through the object is given by the integral:

∫

= dz)z,y,x(n)y,x(s

iop

(14)

where the direction of propagation of the illuminating beam is the z-coordinate

and the analyzed plane wave front is the plane x-y; n

(x,y,z) is the index of

refraction of the object through which light propagates.

The change experienced by the optical path is given by:

[]

∫

=Δ

iop

dzn)z,y,x(n)y,x(s (15)

where t is the thickness of the medium. By assuming that:

n)z,y,x(n= (16)

where n

is the index of refraction of the observed nano-crystals, Eq. (15) then

becomes:

[]

∫

=Δ

iop

dzn)z,y,x(n)y,x(s=(n

-n

)t (17)

By transforming Eq. (17) into phase differences and making n

, where n

is the

index of refraction of the saline solution containing the nano-crystals, one can

write:

t)nn(

=φΔ

(18)

where p is the pitch of the fringes generated by the thickness t of the specimen. In

general, the change of optical path is small and no fringes can be observed. In

order to solve this problem, carrier fringes can be added. An alternative procedure

is the introduction of a grating in the illumination path [16]. In the case of the

nano-crystals, the carrier fringes can be obtained from the FT of the lens hologram

of the analyzed crystals. In the holography of transparent objects, one can start

with recording an image without the transparent object of interest. In a second

stage, one can add the object and then superimpose both holograms in order to

detect the phase changes introduced by the object of interest. In the present

application, reference fringes can be obtained from the background field away

from the observed objects. This procedure presupposes that the systems of carrier

fringes are present in the field independently of the self-luminous objects. This

assumption is verified in the present case since one can observe fringes that are in

the background and enter the nano-crystals experiencing a shift.

Experimental Mechanics in Nano-engineering 287

a) b)

c) d) e)

Fig. 7. NaCl prismatic nano-crystal of length 86 nm: a) Gray-level image (1024x1024

pixels); b) Image of the crystal captured by a colour camera; c) 3-D distribution of light

intensity; d) Isophote lines; e) FT pattern.

Figure 7 illustrates the case of a square cross-section crystal of length 86 nm.

Figure 7b is an image of the crystal recorded by a color camera; the crystal has a

light green tone. The monochromatic image and the color image have different

pixel structures. However, by using features of the images clearly identifiable, a

correspondence between the images could be established and the image of the

nano-crystal located. The figure indicates that the image color is the result of an

electromagnetic resonance and not an emission of light at the same wavelength as

the wavelength of the impinging light.

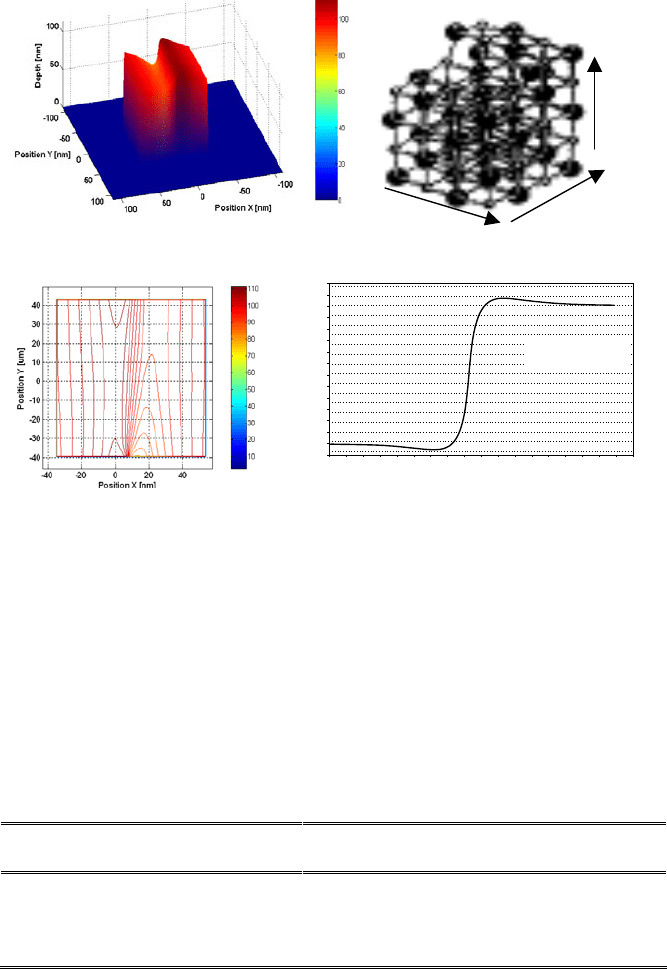
Figure 8a shows the numerical reconstruction of this crystal which is consistent

with the theoretical structure 5×4×4 [19]; Fig. 8c shows the level lines of the top

face of the crystal; Fig. 8d shows a cross section where each horizontal line

corresponds to five elementary cells of NaCl. The theoretical structure has one

step in the depth dimension (Fig. 8b). It is unlikely that the upper face of the nano-

crystal can be exactly parallel to the camera plane. Hence, the crystal shows an

inclination which can be corrected by means of an infinitesimal rotation. This

allows the actual thickness jump in the upper face of the crystal (see the

theoretical structure in Fig. 8b) to be obtained. The jump in thickness is 26 nm out

of a side length of 86 nm: this corresponds to a ratio of 0.313 which is very close

to theory. In fact, the theoretical structure predicts a jump in thickness of one

atomic distance vs. three atomic distances in the transverse direction: that is, a

ratio of 0.333.

Similarly to the case of quantum dots, nano-crystals of different sizes emit light

of different frequencies. The physical reason for this is called quantum

confinement effect. Smaller crystal emit higher energies and therefore their sizes

determine the energy and finally the color. For example, this crystal emits light at

500 nm, in the blue-green range. An explanation of the process of light generation

is given in [11].

288 C.A. Sciammarella, F.M. Sciammarella, and L. Lamberti

a) b)

100

102

104

106

108

110

112

114

116

118

120

0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90

Depth X

[nm]

Thickness Z

[nm]

Spacing between dotted

lines corresponds to the

size of 3 elementary cells

Depth (X)

Thickness (Z)

Width (Y)

Fig. 8. a) Numerical reconstruction of a NaCl nano-crystal of length 86 nm, the crystal is

inclined with respect to the image plane; b) Schematic of the theoretical structure 5x4x4; c)

Level lines; d) Rotated cross section of the upper face of the nano-crystal: the spacing

between dotted lines corresponds to the size of three elementary cells.

Table 2 shows the experimental aspect ratios measured for some nano-crystals:

these values are compared with the theoretical aspect ratios. The table also

provides the error analysis of these results. Thicknesses reported in Table 3 are the

average values shown in Table 2.

Table 2. Aspect ratio of the observed nano-crystals: experiments vs. theory

Nano-crystal

length (nm)

Experimental

dimensions (nm)

Experimental

aspect ratio

Theoretical aspect

ratio

54 72 x 54 x 53 5.43 x 4.08 x 4 5 x 4 x 4

55 55 x 45 x 33.5 4.93 x 4.03 x 3 5 x 5 x 3

86 104 x 86 x 86 4.84 x 4 x 4 5 x 4 x 4

120 120 x 46 x 46 7.83 x 3 x 3 8 x 3 x 3

Mean error on aspect ratios = 4.59%; Standard deviation on aspect ratios = ± 6.57%.