Кошкин Г.М. Основы страховой математики
Подождите немного. Документ загружается.


µ
x
=
f(x)
s(x)
=
q
n
p
n
+ (x − n)q
n
, n < x < n + 1.
80
1
2
81
1
2
s(x) = (n + 1 − x)s(n) + (x − n)s(n + 1), n ≤ x ≤ n + 1,
s
80
1
2
=
81 − 80
1
2
s(80) +
80
1
2
− 80
s(81) = 0, 5(s(80) + s(81)),
s
81
1
2
= 0, 5(s(81) + s(82)).
P
1
2
< T(80) < 1
1
2
=
s
80
1
2
− s
81
1
2
s(80)
=
= 0, 5
s(80) + s(81) − s(81) − s(82)
s(80)
=
= 0, 5
1 −
s(82)
s(80)
= 0, 5
1 −
s(82)
s(81)
˙
s(81)
s(80)
!
=
= 0, 5(1 − p
81
p
80
) = 0, 5(1 − (1 − q
81
)(1 − q
80
)) =
= 0, 5(1 − (1 − 0, 12548)(1 − 0, 11672)) =
= 0, 5(1 − 0, 87452
˙
0, 88328) = 0, 11378.
τ = {X} {X}
X X
X = K(0)+τ K(0) = [X]
τ
τ
n
P{τ ≤ t|K(0) = n} = P{X − K(0) ≤ t|K(0) = n} =

= P{X ≤ t + n|n ≤ X < n + 1} =
P{X ≤ t + n, n ≤ X < n + 1}
P{n ≤ X < n + 1}
=
=
P{n ≤ X ≤ n + t}
P{n ≤ X < n + 1}
=
s(n) − s(n + t)
s(n) − s(n + 1)
, 0 < t < 1.
s(n + t), l
n+t
n 0 < t < 1,
s(x) x = n + t,
P{τ ≤ t|K(0) = n} =
=
s(n) − [(n + 1 − n − t)s(n) + (n + t − n)s(n + 1)]
s(n) − s(n + 1)
=
=
t(s(n) − s(n + 1))
s(n) − s(n + 1)
= t, 0 < t < 1.
µ
t|·
=
f(t|·)
1 − F (t|·)
=
1
1 − t
P{τ ≤ t|K(0) = n} n
P(τ ≤ t)
K(0) τ
P{τ ≤ t|K(0) = n} =
s(n) − s(n + t)
s(n) − s(n + 1)
=
=
s(n) − s(n)p
n+t−n
n
s(n) − s(n + 1)
=
s(n)(1 − p
t
n
)
s(n) − s(n + 1)
=
1 − p
t
n
1 − p
n
, 0 < t < 1.
f(t|·) = F
0
(t|·) =
−p
t
n
p
n
1 − p
n
,
s(t|·) = 1 − F (t|·) = 1 −
1 − p
t
n
1 − p
n
=
1 − p
n
− 1 + p
t
n
1 − p
n
=
p
n
(p
t−1
n
− 1)
1 − p
n
,
µ
t|·
=
f(t|·)
s(t|·)
=
−p
t
n
p
n
p
n
(p
t−1
n
− 1)
=
−p
t−1
n
p
n
p
t−1
n
− 1
.

f(t|·), s(t|·), µ
(
t|·)
q
n
= 1 −p
n
q
n
τ
n
a(n) = E{τ|K(0) = n} =
Z
1
0
P{τ > t|K(0) = n}dt.
P{τ > t|K(0) = n} = 1 − P{τ ≤ t|K(0) = n} =
= 1 −
s(n) − s(n + t)
s(n) − s(n + 1)
=
s(n) − s(n + 1) − sn) + s(n + t)
s(n) − s(n + 1)
=
=
s(n + t) − s(n + 1)
s(n) − s(n + 1)
.
a(n) =
1
s(n) − s(n + 1)
Z
1
0
[s(n + t) − s(n + 1)] .
a(n)
a(n) =
R
1
0
[(n + 1 − n − t)s(n) + (n + t − n)s(n + 1) − s(n + 1)]
s(n) − s(n + 1)
=
=
R
1
0
[(1 − t)s(n) + ts(n + 1) − s(n + 1)] =
R
1
0
(1 − t)
s(n) − s(n + 1)
=
1
2
,
a(n)
a(n) =
1
s(n) − s(n + 1)
Z
1
0
[s(n)p
n+t−n
n
− s(n + 1)] =

=
s(n)
s(n) − s(n + 1)
Z
1
0
p
t
n
− p
n
=
1
q
n
"
p
t
n
p
n
1
0
− p
n
#
=
=
1
q
n
p
n
− 1
p
n
− p
n
=
1
q
n
−p
n
−
q
n
p
n
= −
1
p
n
−
p
n
q
n
.
p
n
= 1 − q
n
, q
n
(1 − x) = −x −
x
2
2
−
x
3
3
− ··· − −
x
n
n
+ o(x
n
),
p
n
q
n
p
n
= −q
n
−
q
2
n
2
−
q
3
n
3
− ...,
a(n)
a(n) =
1
2
−
q
n
12
+ O(q
2
n
) =
1
2
−
q
n
12
+ o(q
n
).
−
p
n
q
n
−
1
p
n
= −
1 − q
n
q
n
+
1
q
n
+
q
2
n
2
+
q
3
n
3
+ ...
=
= 1 +
1
q
n
+
q
2
n
2
+
q
3
n
3
+ ...
−
1
q
n
= 1 −
q
2
n
2
+
q
3
n
3
+ ...
q
2
n
+
q
3
n
2
+
q
4
n
3
+ ...
,
q
2
n
2
, q
2
n
,
−
p
n
q
n
−
1
p
n
= 1 −
"
1
2
+
1
q
2
n
q
3
n
3
+ ...
−
q
2
n
2
q
4
n
q
3
n
2
+ ...
#
=
=
1
2
−
q
n
3
+
q
n
4
+ o(q
n
) =
1
2
−
q
n
12
+ o(q
n
),

q
n
O(q
2
n
) :
a(n) = 1 −
1
q
2
n
q
3
n
3
+
q
4
n
4
+ ...
+
1
2q
2
n
q
3
n
2
+
q
4
n
3
+ ...
=
=
1
2
−
q
n
3
+
q
n
4
−
q
2
n
4
+
q
2
n
6
+ ... =
1
2
−
q
n
12
−
q
2
n
12
+ o(q
2
n
).
a(n) =
1
s(n) − s(n + 1)
Z
1
0
s(n + 1)
p
n
+ tq
n
− s(n + 1)
=
=
s(n + 1)
s(n) − s(n + 1)
Z
1
0
1
p
n
+ tq
n
− 1
=
p
n
q
n
Z
1
0
1
p
n
+ tq
n
− 1
=
=
p
n
q
n
"
(p
n
+ tq
n
)
q
n
1
0
− 1
#
=
p
n
q
n
−
p
n
q
n
− 1
=
−
p − n
q
2
n
(q
n
+ p − n) =
q
n
− 1
q
2
n
q
n
− q
n
−
q
2
n
2
−
q
3
n
3
− ...
=
= (q
n
− 1)
−
1
2
−
q
n
3
−
q
2
n
4
− ...
=
1
2
−
q
n
2
+
q − n
3
−
q
2
n
3
+
q
2
n
4
+ o(q
n
) =
=
1
2
−
q
n
6
−
q
2
n
12
+ o(q
n
).
b(n) = D{τ|K(0) = n} =
=
2
s(n) − s(n + 1)
Z
1
0
[s(n + t) − s(n + 1)] − a
2
(n).
b(n)
b(n) =
2
s(n) − s(n + 1)
Z
1
0
t(1 − t)[s(n) − s(n + 1)] −
1
4
=
= 2
Z
1
0
(t − t
2
) −
1
4
= 2
1
2
−
1
3
−
1
4
= 1 −
2
3
−
1
4
=
1
12
.
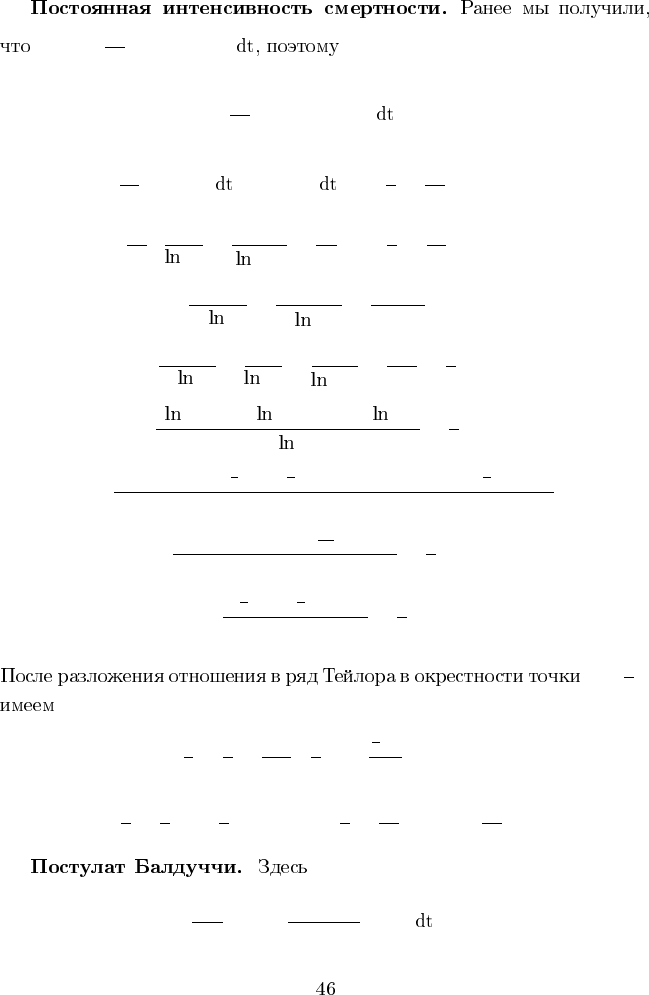
a(n) =
1
q
n
Z
1
0
[p
t
n
− p
n
]
b(n) =
2
q
n
Z
1
0
t(p
t
n
− p
n
) − a
2
(n) =
=
2
q
n
Z
1
0
tp
t
n
−
Z
1
0
tp
n
−
1
2
−
q
n
12
+ o(q
n
)
2
=
=
2
q
n
p
n
p
n
−
p
n
− 1
2
p
n
−
p
n
2
−
1
4
−
q
n
12
+ o(q
n
)
=
= 2
1 − q
n
q
n
p
n
+
q
n
q
n
2
p
n
−
1 − q
n
2q
n
− [...] =
= 2
1
q
n
p
n
−
1
p
n
+
1
2
p
n
−
1
2q
n
+
1
2
− [...] =
= 2
2 p
n
− 2q
n
p
n
+ 2q
n
−
2
p
n
2q
n
2
p
n
+
1
2
− [...] =
= 2
−2q
n
− q
2
n
−
2
3
q
3
n
−
1
2
q
4
n
− ... + 2q
2
n
+ q
3
n
+
2
3
q
4
n
+ ...
2q
3
n
+ 2q
4
n
+ ...
+
+2
2q
n
− q
2
n
− q
3
n
−
11
12
q
4
n
− ...
2q
3
n
+ 2q
4
n
+ ...
+
1
2
− [...] =
= 2
−
2
3
q
3
n
−
3
4
q
4
n
− ...
2q
3
n
+ 2q
4
n
+ ...
+
1
2
− [...].
−
2
3
q
3
n
, 2q
3
n
,
b(n) = 2
1
2
−
1
3
−
1
2q
3
n
·
3
4
q
4
n
+
2
3
q
3
n
4q
6
n
2q
4
n
− ...
− [...] =
= 2
1
6
−
3
8
q
n
+
1
3
q
n
− ...
−
1
4
−
q
n
12
+ ...
=
1
12
+ o(q
n
).
b(n) =
2p
n
q
n
Z
1
0
t
1
p
n
+ tq
n
− 1
− a
2
(n) =
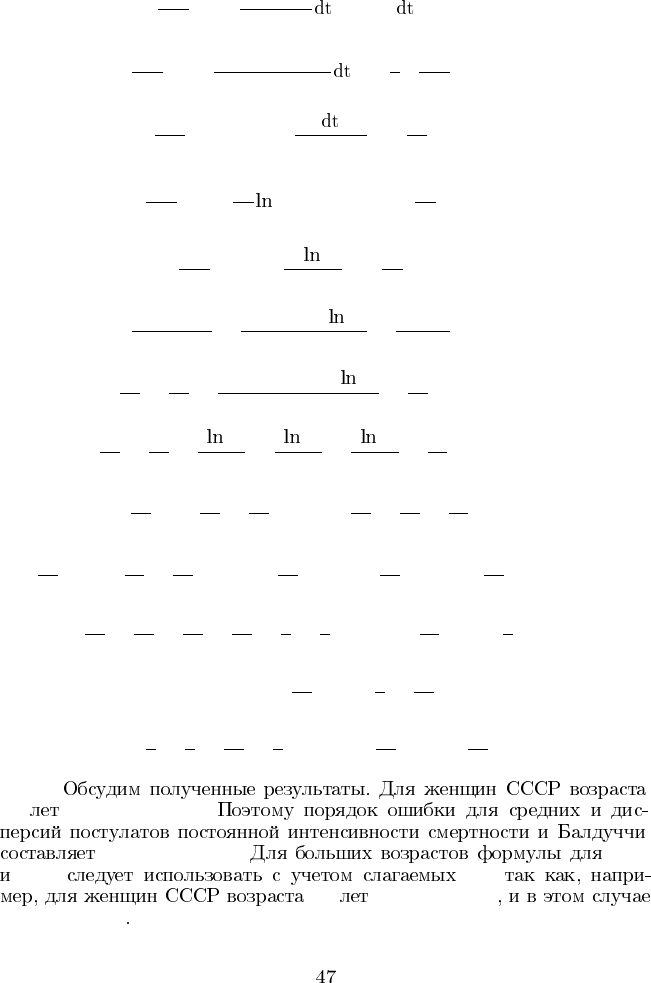
=
2p
n
q
n
Z
1
0
t
p
n
+ tq
n
−
Z
1
0
t
− a
2
(n) =
=
2p
n
q
2
n
Z
1
0
p
n
+ tq
n
− p
n
p
n
+ tq
n
−
1
2
·
2p
n
q
n
− a
2
(n) =
=
2p
n
q
2
n
1 − p
n
Z
1
0
p
n
+ tq
n
−
p
n
q
n
− a
2
(n) =
=
2p
n
q
2
n
"
1 −
p
n
q
n
(p
n
+ tq
n
)
1
0
#
−
p
n
q
n
− a
2
(n) =
=
2p
n
q
2
n
1 + p
n
p
n
p
n
q
n
−
p
n
q
n
− a
2
(n) =
=
2(1 − q
n
)
q
2
n
+
2(1 − q
n
)
2
p
n
q
3
n
−
1 − q
n
q
n
− a
2
(n) =
=
2
q
2
n
−
2
q
n
+
2(1 − 2q + q
2
n
) p
n
q
3
n
−
1
q
n
+ 1 − a
2
(n) =
=
2
q
2
n
−
2
q
n
+
2 p
n
q
3
n
−
4 p
n
q
2
n
+
2 p
n
q
n
−
1
q
n
+ 1 − a
2
(n) =
=
2
q
3
n
q
2
n
−
2
q
n
+
2
q
3
n
−q
n
−
q
2
n
2
−
q
3
n
3
−
q
4
n
4
− ...
+
+
4
q
2
n
q
n
+
q
2
n
2
+
q
3
n
3
+ ...
+
2
q
n
−q
n
−
q
2
n
2
− ...
−
1
q
n
+ 1 − a
2
(n) =
=
2
q
2
n
−
2
q
n
−
2
q
2
n
−
1
q
n
−
2
3
−
1
2
q
n
− ... +
4
q
n
+ 2 +
4
3
q
n
+ ...−
−2 − q
n
− ... −
1
q
n
+ 1 −
1
4
+
q
n
6
+ ... =
= 1 −
1
4
−
2
3
−
q
n
2
+
4
3
q
n
− q
n
+
q
n
6
+ ... =
1
12
+ o(q
n
).
30 q
30
= 0, 00106.
O(q
2
30
) ≈ 10
−6
. a(n)
b(n) q
2
n
,
82 q
82
= 0, 10155
O(q
2
82
) ≈ 10
−2

K(0) τ,
◦
e
x
≈ e
x
+
1
2
,
DT (x) ≈ DK(0) +
1
12
.
L
x
T
x
a(x)
L
x
T
x
L
x
x x + 1 x
l
0
x x+1
x x + 1 d
x
a(x)
x+1 l
x+1
·1 = l
x+1
L
x
= d
x
a(x) + l
x+1
=
d
x
s(x) − s(x + 1)
Z
1
0
[s(x + t) − s(x + 1)] + l
x+1
=
=
d
x
l
x
− l
x+1
Z
1
0
[l
x+t
− lx + 1] + l
x+1
=
=
Z
1
0
[l
x+t
− lx + 1] + l
x+1
=
Z
1
0
l
x+t
.
l
x
L
x
a(x)
L
x
− l
x+1
= d
x
a(x),
a(x) =
L
x
− l
x+1
l
x
− l
x+1
=
L
x
− l
x+1
d
x
.

a(20), a(80), a(106), a(107), a(108).
a(20) =
L
20
− l
21
d
2
0
=
97682 − 97623
118
=
59
118
= 0, 5;
a(80) =
L
80
− l
81
d
8
0
=
41694 − 40208
2972
=
1486
2972
= 0, 5;
a(100) =
983 − 815
335
= 0, 501; a(106) =
99 − 78
41
= 0, 512;
a(107) =
99 − 78
41
= 0, 512; a(108) =
42 − 33
18
= 0, 5.
a(i) ∼ 0, 5,
T
x
l
0
(x, ∞)
T
x
= l
0
E[(X − x)I(x − x > 0)] = l
0
Z
∞
0
(X − x)dP{X − x ≤ t} =
= l
0
Z
∞
0
P{X − x > t} = l
0
Z
∞
0
P{X > x + t} =
= l
0
Z
∞
0
s(x + t) = l
0
Z
∞
x
s(u) .
◦
e
x
= ET (x)
◦
e
x
= ET (x) =
1
s(x)
Z
∞
0
s(u) =
1
l
0
s(x)
l
0
Z
∞
0
s(u) =
T
x
l
x
.
◦
e
20
,
◦
e
80
.
◦
e
20
=
T
20
l
2
0
=
5420937
97741
= 55, 462;
◦
e
80
=
T
80
l
8
0
=
344612
43180
= 7, 98.

L
n
, n ≥ x,
T
x
:
T
x
= l
0
Z
∞
x
s(u) = l
0
∞
X
k=0
Z
x+k+1
x+k
s(u) =
= l
0
∞
X
k=0
Z
1
0
s(x + k + t) =
∞
X
k=0
Z
1
0
l
x+k+t
=
∞
X
k=0
L
x+k
=
∞
X
n=x
L
n
.
T
x
=
∞
X
n=x
L
n
.
T
100
T
105
.
T
105
:
T
105
= L
105
+ L
106
+ L
107
+ L
108
+ L
109
+
∞
X
n=110
L
n
= L
105
+ L
106
+ L
107
+
+L
108
+ L
109
+ (T
109
−L
109
) = 150 + 99 + 64 + 42 + 27 + (73 − 27) = 428.
T
100
= T
105
+ L
104
+ L
103
+ L
102
+ L
101
+ L
100
=
= 428 + 223 + 330 + 481 + 692 + 983 = 3137.
77
5
12
78
11
12
