Кошкин Г.М. Основы страховой математики
Подождите немного. Документ загружается.


x = (n/k)
1/(n+1)
f(x) =
x
a
2
e
−
x
a
, x ≥ 0.
s(x) =
x + a
a
e
−
x
a
,
µ
x
=
x
a(x + a)
.
s(x) x
x
s
1
(x)
x
s
2
(x)

x
s
3
(x)
µ
x
kx
n
µ
x
Be
αx
, α > B > 0
s
1
(x) = e
−x
3
/12
, x ≥ 0;
s
2
(x) =
1 −
x
ω
α
, 0 ≤ x < ω, α > 0.
s
2
(x) α = 1
µ
ix
, f
i
(x)
F
i
(x),
s
i
(x), i = 1, 2.
10 30

10
f(x) =
x
a
2
e
−x/a
.
f(x)
s(x)
µ
x
,
◦
e
◦
.
l
0
50 70
s
i
(x), i = 1, 2, 3,
n = 2, 4.
k
n = 2, 4,
n
k
n
f(x) =
x
a
2
e
−x/a
, x ≥ 0.
F
x
(t)
T (x) = X − x X, x
F
x
(t) = P (T (x ≤ t)).

f
x
(t) =
d
dt
F
x
(t)
1
a
e
−t/a
t
a
2
e
−t/a
.
P (T (x) > t), lim
x→∞
P (T (x) > t)
x.

x
X, T (x) =
X − x. T (x),
X −x
X > x :
F
x
(t) = P(T (x) ≤ t) = P(X − x ≤ t|X > x) =
= P(X ≤ x + t|X > x) =
t
q
x
=
P(X ≤ x + t
T
X > x)
P(X > x)
=
=
P(x < X ≤ x + t)
P(X > x)
=
F (x + t) − F (x)
1 − F (x)
.
l
x
l
x+t
,
F
x
(t)
F
x
(t) =
s(x) − s(x + t)
s(x)
=
l
x
/l
◦
− l
x+t
/l
◦
l
x
/l
◦
=
l
x
− l
x+t
l
x
.
f
x
(t)
T (x) :
f
x
(t) =
d
dt
F
x
(t) =
f(x + t)
1 − F (x)
, 0 ≤ t < ∞.
I
x
(a, b] =
1, x ∈ (a, b]
0, x /∈ (a, b]
.
f(x) =
I
x
(0, ω)
ω
, s(x) = I
x
(−∞, ω) −
x I
x
(0, ω)
ω
.

0 < X < ω, 0 < T (x) < ω −x,
F
x
(t) =
t
ω −x
I
t
(0, ω −x) + I
t
[ω −x, ∞),
t ∈ (0, ω −x)
f
x
(t) =
d
dt
t
ω −x
=
1
ω −x
, t ∈ (0, ω −x],
T (x)
(0, ω −x).
µ
t
= A + B e
αt
, s(x) =
−
Z
x
0
µ
t
dt
= [−Ax − B (e
α x
− 1)/α] ,
f(x) = −s
0
(x) = [A + B e
α x
] [−Ax − B (e
α x
− 1)/α] ,
f(x + t) = [A + B e
α (x+t)
]
h
−A(x + t) − B (e
α (x+t)
− 1)/α
i
.
f
x
(t) =
f(x + t)
s(x)
= [A + B e
α x
e
α t
]
−At − B e
α x
(e
α t
− 1)/α
,
T (x)
A
x
= A, B
x
= B e
α x
, α
x
= α.
T (x)
t
q
x
,
tx
, q
x
, p
x
,
t|u
q
x
,
t|
q
x
P(T (x) ≤ t)
P(T (x) > t),
t
q
x tx
,
t
q
x
= P(T (x) ≤ t) =
s(x) − s(x + t)
s(x)
,
tx
= P(T (x) > t) = 1 −
t
q
x
=
s(x + t)
s(x)
.
t
q
x
x
(x, x + t],
tx
x + t.

t = 1
t
q
x tx
q
x
= P(T (x) ≤ 1) =
s(x) − s(x + 1)
s(x)
=
l
x
− l
x+1
l
x
,
x
= P(T (x) > 1) =
s(x + 1)
s(x)
=
l
x+1
l
x
.
q
x x
q
x
x
p
x
q
x
=
d
x
l
x
.
q
x
l
x
= l
◦
s(x), d
x
≈ l
◦
f(x),
q
x
≈
f(x)
s(x)
= µ
x
, q
x
l
x
= l
◦
s(x) l
◦
s(x)
x;
d
x
≈ l
◦
f(x)
l
◦
f(x)
x;
q
x
≈
f(x)
s(x)
= µ
x
µ
x
.
x t u
t|u
q
x
= P(t < T (x) ≤ t + u),
t
q
x
,
tx
,
s(x) :
t|u
q
x
= P(t < T (x) ≤ t + u) =

= P(T (x) ≤ t + u) − P(T (x) ≤ t) =
t+u
q
x
−
t
q
x
,
t|u
q
x
= P(t < T (x) ≤ t + u) =
= P(T (x) > t) − P(T (x) > t + u) =
t
p
x
−
t+u
p
x
,
t|u
q
x
=
s(x + t) − s(x + t + u)
s(x)
.
u = 1
t|
q
x
=
t+1
q
x
−
t
q
x
=
t
p
x
−
t+1
p
x
=
s(x + t) − s(x + t + 1)
s(x)
.
x
◦
e
x
= ET (x);
ET (0) = EX =
◦
e
◦
,
◦
e
◦
◦
e
x
x > 0.
T (x)
◦
e
x
= ET (x) =
Z
∞
0
t dF
x
(t) =
Z
∞
0
t dP(T (x) ≤ t) =
=
Z
∞
0
P(T (x) > t) dt =
Z
∞
0
t
p
x
dt.
Z
∞
0
t
p
x
dt =
1
s(x)
Z
∞
0
s(x + t) dt =
1
s(x)
Z
∞
x
s(u) du,
◦
e
x
=
1
s(x)
Z
∞
x
s(u) du.
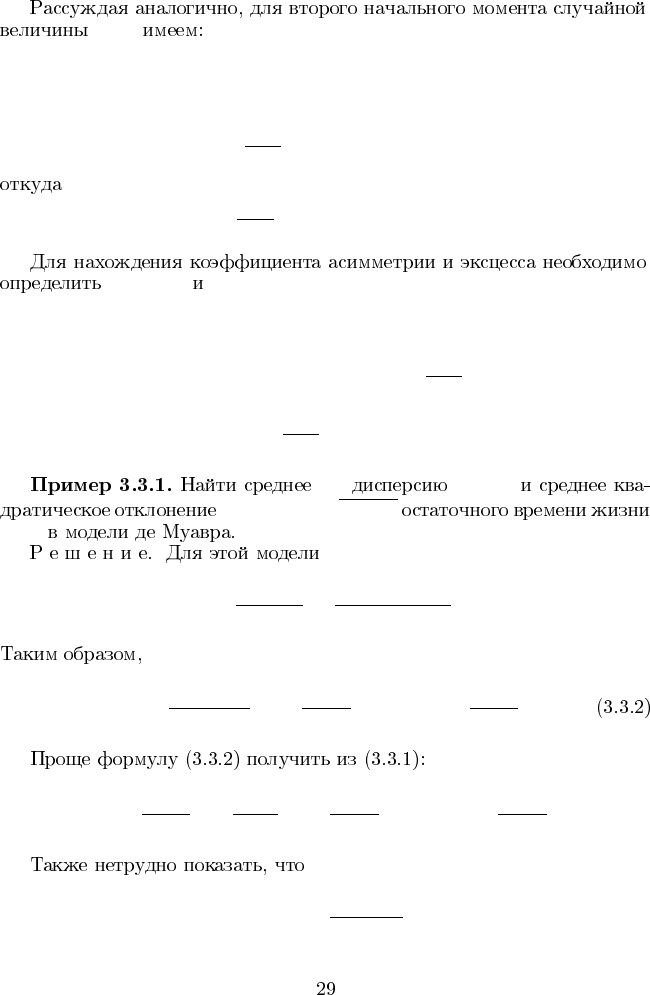
T (x)
E[T (x)]
2
= 2
Z
∞
0
t P(T (x) > t) dt = 2
Z
∞
0
t
t
p
x
dt =
=
2
s(x)
Z
∞
0
t s(x + t) dt,
DT (x) =
2
s(x)
Z
∞
0
t s(x + t) dt −
◦
e
x
2
.
E[T (x)]
3
E[T (x)]
4
:
E[T (x)]
3
=
= 3
Z
∞
0
t
2
P(T (x) > t) dt = 3
Z
∞
0
t
2
t
p
x
dt =
3
s(x)
Z
∞
0
t
2
s(x + t) dt,
E[T (x)]
4
=
4
s(x)
Z
∞
0
t
3
s(x + t) dt.
◦
e
x
, DT (x)
σ(T (x)) =
p
DT (x)
T (x)
P(T (x) > t) =
t
p
x
=
s(x + t)
s(x)
=
1 − (x + t)/ω
1 − x/ω
, 0 ≤ t ≤ ω −x.
◦
e
x
=
Z
ω−x
0
ω −x − t
ω −x
dt =
−1
ω −x
Z
0
ω−x
u du =
ω −x
2
.
◦
e
x
=
ω
ω −x
Z
ω
x
ω −t
ω
dt =
−1
ω −x
Z
0
ω−x
u du =
ω −x
2
.
DT (x) =
(ω −x)
2
12
.

n n
n
n
n
(T (x), n)
◦
e
x:ne
:
◦
e
x:ne
= E (T (x), n).
P( (T (x), n) >
t). t < n (T (x), n) > t
T (x) > t,
P( (T (x), n) > t) =
t
p
x
, 0 ≤ t < n
0, t ≥ n.
◦
e
x:ne
=
Z
n
0
t
p
x
dt =
1
s(x)
Z
n
0
s(x + t) dt =
1
s(x)
Z
x+n
x
s(u) du.
D (T (x), n) = 2
Z
n
0
t
t
p
x
dt − (
◦
e
x:ne
)
2
=
2
s(x)
Z
n
0
t s(x + t) dt − (
◦
e
x:ne
)
2
.
x + n < ω,
◦
e
x:ne
=
1
s(x)
Z
x+n
x
s(u) du =
1
1 − x/ω
Z
x+n
x
(1 − u/ω) du =
=
1
ω −x
Z
x+n
x
(ω −u) du =
2n(ω −x) − n
2
2(ω −x)
= n −
n
2
2(ω −x)
.
