Кошкин Г.М. Основы страховой математики
Подождите немного. Документ загружается.


x
s
1
(x)
x
s
2
(x)
x
s
3
(x)
X
ω = 100 − 120
s(x) = 0, x > ω.
x ≤ ω. s(x),
s(x) P{X > ω}
s(x)
l
x
l
◦
l
◦
= 10000
l
◦
= 100000
X
1
, X
2
, . . . , X
l
◦
. A
I(A) = {1, A ; 0, }.

x,
L(x) =
l
◦
X
i=1
I(X
i
> x),
l
x
:
l
x
= El
x
=
l
◦
X
i=1
EI(X
i
> x) =
l
◦
X
i=1
P(X
i
> x) =
l
◦
X
i=1
s(x) = l
◦
s(x),
l
x
= l
◦
· s(x)
l
x
x
s(x) l
◦
;
s(x) = l
x
/l
◦
x
l
14
= 95, 438
s(14) = 0, 95438
l
◦
= 1000,
l
0
= 1000

(x, x+
t)
t
D
x
= L(x) − L(x + t) =
l
◦
X
i=1
I(x < X
i
≤ x + t),
x x+t
l
◦
t
d
x
t
d
x
= E
t
D
x
t
d
x
= E[L(x) − L(x + t)] = l
x
− l
x+t
= l
0
[s(x) − s(x + t)],
s(x)−s(x+t) = P(x < X
i
≤ x+t)
(x, x + t].
1
d
x
d
x
= l
x
− l
x+1
d
x
l
x
l
x+1
,
d
x
f(x) = F
0
(x) = −s
0
(x)
X,
d
x
x
f(x)
l
◦
,
d
x
≈ l
◦
f(x)
s(x) = s(x + 1) − s
0
(ξ),
ξ ∈ (x, x + 1). s(x)
d
x
= −l
◦
s
0
(ξ) ≈ −l
◦
s
0
(x) = l
◦
f(x).
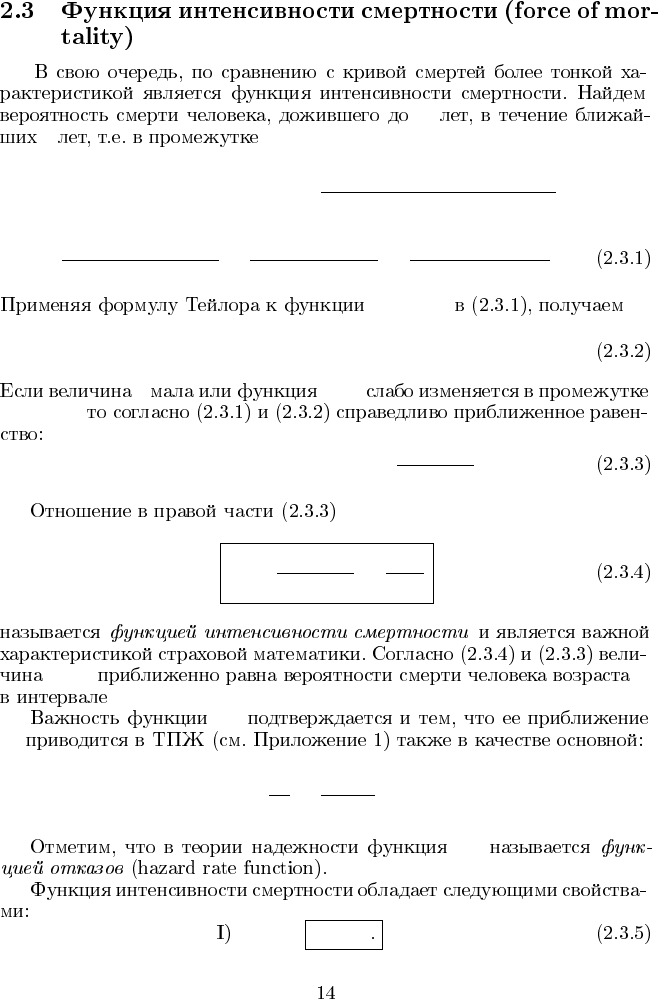
x
t (x, x + t] :
P(x < X ≤ x + t|X > x) =
P(x < X ≤ x + t ∩ X > x)
P(X > x)
=
=
P(x < X ≤ x + t)
P(X > x)
=
s(x) − s(x + t)
s(x)
=
F (x + t) − F (x)
1 − F (x)
.
F (x + t)
F (x + t) −F (x) = F (x) + F
0
(ξ) ·t −F (x) = f(ξ) ·t, ξ ∈ (x, x + t).
t f(ξ)
(x, x + t),
P(x < X ≤ x + t|X > x) ≈
f(x)
1 − F (x)
· t.
µ
x
=
f(x)
1 − F (x)
=
f(x)
s(x)
µ
x
·t x
(x, x + t).
µ
x
q
x
q
x
=
d
x
l
x
≈
l
◦
f(x)
l
◦
s(x)
= µ
x
.
µ
x
µ
x
≥ 0

Z
∞
0
µ
u
du = +∞
s(+∞) = 0, s(0) = 1,
Z
∞
0
µ
u
du = −
Z
∞
0
ds(u)
s(u)
= −ln s(u))
∞
0
= +∞.
s(x) = e
−
R
x
0
µ
u
du
F (x) = 1 − e
−
R
x
0
µ
u
du
µ
u
= −s
0
(u)/s(u)
du
µ
u
du = −
s
0
(u)du
s(u)
= −
ds(u)
s(u)
,
x
Z
x
0
µ
u
du = −
Z
x
0
ds(u)
s(u)
= − s(u)
x
0
=
= −( s(x) − s(0)) = −( s(x) − 1) = − s(x),
s(x) = 1 − F (x) = e
−
R
x
0
µ
u
du
.
♠
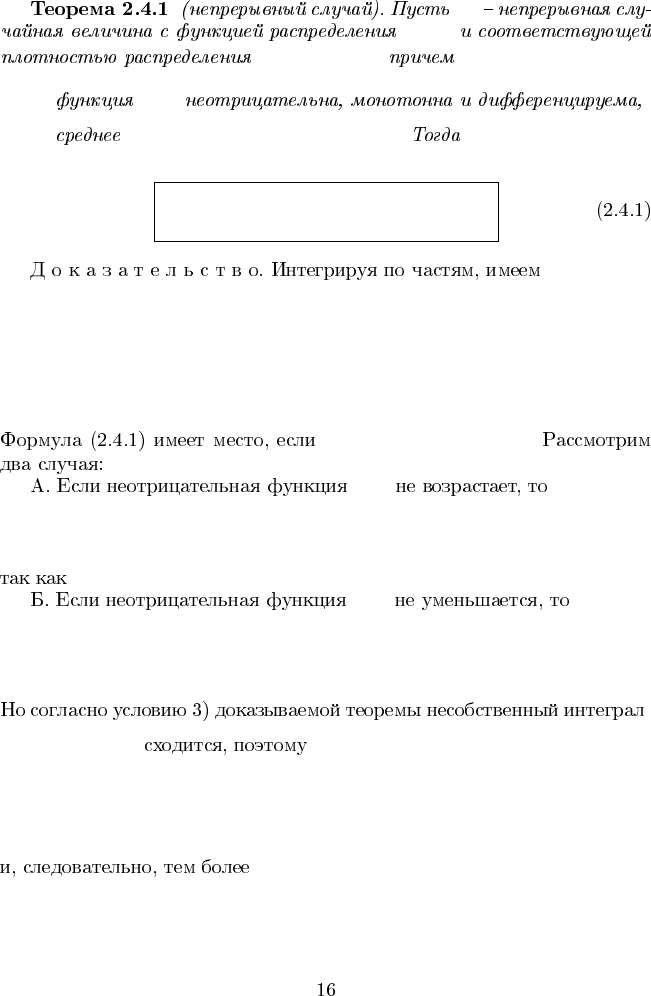
X
F (x)
f(x) = F
0
(x),
1) F (0) = 0,
2) z(x)
3) Ez(X) =
Z
∞
0
z(x)f(x)dx < ∞.
Ez(X) = z(0) +
Z
∞
0
z
0
(t)[1 − F (t)]dt.
Z
x
0
z(t)f(t)dt = −
Z
x
0
z(t)d[1 − F (t)] =
= −z(t)[1 − F (t)]|
x
0
+
Z
x
0
[1 − F (t)]z
0
(t)dt.
lim
t→∞
z(t)[1 − F (t)] = 0.
z(t)
lim
t→∞
z(t)[1 − F (t)] ≤ z(0) lim
t→∞
[1 − F (t)] = 0,
lim
t→∞
F (t) = 1.
z(t)
0 ≤ z(t)[1 − F (t)] = z(t)
Z
∞
t
f(s)ds ≤
Z
∞
t
z(s)f(s)ds.
Z
∞
0
z(x)f(x)dx
lim
t→∞
Z
∞
t
z(s)f(s)ds = 0,
lim
t→∞
z(t)[1 − F (t)] = 0. ♠

F (k) p(k) =
P(Y = k) = F (k) − F (k −1) = ∆F (k −1),
1) z(k)
2) Ez(K) =
∞
X
k=0
z(k)p(k) < ∞.
Ez(K) = z(0) +
∞
X
k=0
[1 − F (k)]∆z(k)
k−1
X
j=0
z(j)p(j) = −
k−1
X
j=0
z(j)∆[1 − F (j − 1)] =
= −z(j)[1 − F (j − 1)]|
k
0
+
k−1
X
j=0
[1 − F (j)]∆z(j).
lim
k→∞
z(k)[1−F(k−1)] = 0.
z(k)
lim
k→∞
z(k)[1 − F (k −1)] ≤ z(0) lim
k→∞
[1 − F (k −1)] = 0,
lim
k→∞
F (k −1) = 0.
z(k)
0 ≤ z(k)[1 − F (k −1)] = z(k)
∞
X
j=k
p(j) ≤
∞
X
j=k
z(j)p(j).
∞
X
k=0
z(k)p(k)
lim
k→∞
∞
X
j−k
z(j)p(j) = 0,
lim
k→∞
z(k)[1 − F (k −1)] = 0. ♠

X
◦
e
◦
= EX =
Z
∞
0
xf(x)dx
◦
e
◦
X
DX = E(X−
◦
e
◦
)
2
= EX
2
− (
◦
e
◦
)
2
=
Z
∞
0
x
2
f(x)dx −
◦
e
◦
2
γ =
E(X−
◦
e
◦
)
3
(DX)
3/2
oe =
E(X−
◦
e
◦
)
4
(DX)
2
− 3
◦
e
◦
DX
◦
e
◦
,
γ > 0
X, oe ≈ 0, X
oe = 0
X
◦
e
◦
= EX z(x) =
x, z(0) = 0, z
0
(x) = 1
EX =
Z
∞
0
(1 − F (x))dx =
Z
∞
0
s(x)dx

EX
2
z(x) = x
2
, z(0) = 0, z
0
(x) = 2x
EX
2
= 2
Z
∞
0
x(1 − F (x))dx = 2
Z
∞
0
xs(x)dx
ω ω,
0 < x < ω
f(x) =
1
ω
, F (x) =
x
ω
, s(x) = 1 −
x
ω
, µ
x
=
f(x)
s(x)
=
1
ω −x
.
µ
x
=
f(x)
s(x)
= B e
αx
,
α > B > 0
s(x) =
−
Z
x
0
µ
u
du
=
−
Z
x
0
B e
αu
du
=
= [−B (e
αx
− 1)/α] ,
f(x) = µ
x
s(x) = B [αx − B (e
αx
− 1)/α]

x = (ln α − ln B)/α
α B.
x
0,25
(ln α − ln B)/α = 78, 3,
1 −
−B (e
α33,4
− 1)/α
= 0, 25.
µ
x
= A + B e
α x
,
A
B e
α x
s(x) =
−
Z
x
0
(A + B e
αu
)du
= [−Ax − B (e
α x
− 1)/α] ,
f(x) = −s
0
(x) = [A + B e
α x
] [−Ax − B (e
α x
− 1)/α] .
µ
x
= k x
n
,
s(x) =
−
Z
x
0
ku
n
du
=
−
k
n + 1
x
n+1
f(x) = −s
0
(x) = kx
n
−
k
n + 1
x
n+1
