Кошкин Г.М. Основы страховой математики
Подождите немного. Документ загружается.



L
1



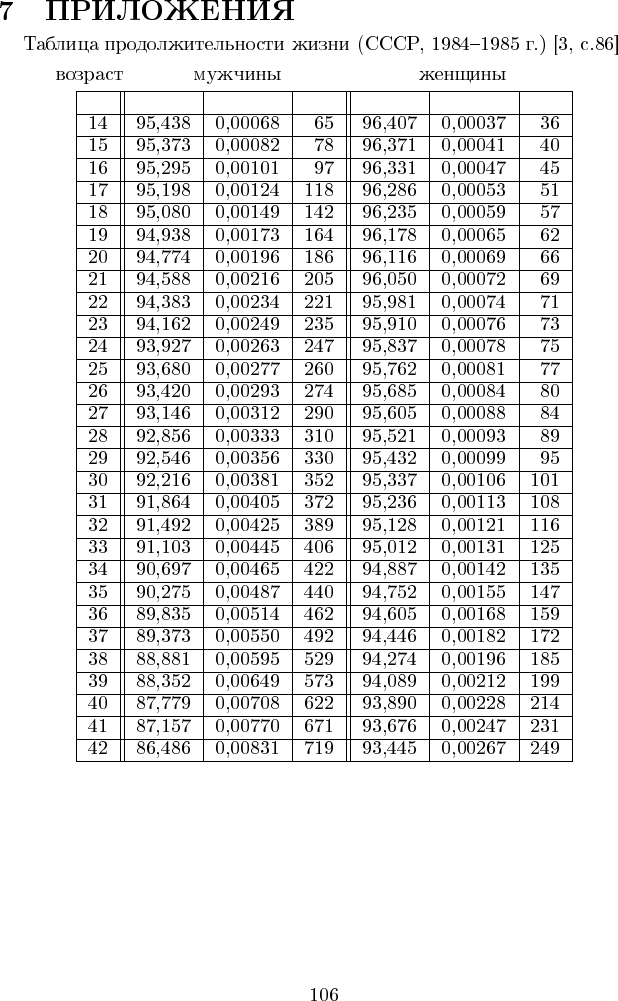
x l
x
q
x
d
x
l
x
q
x
d
x
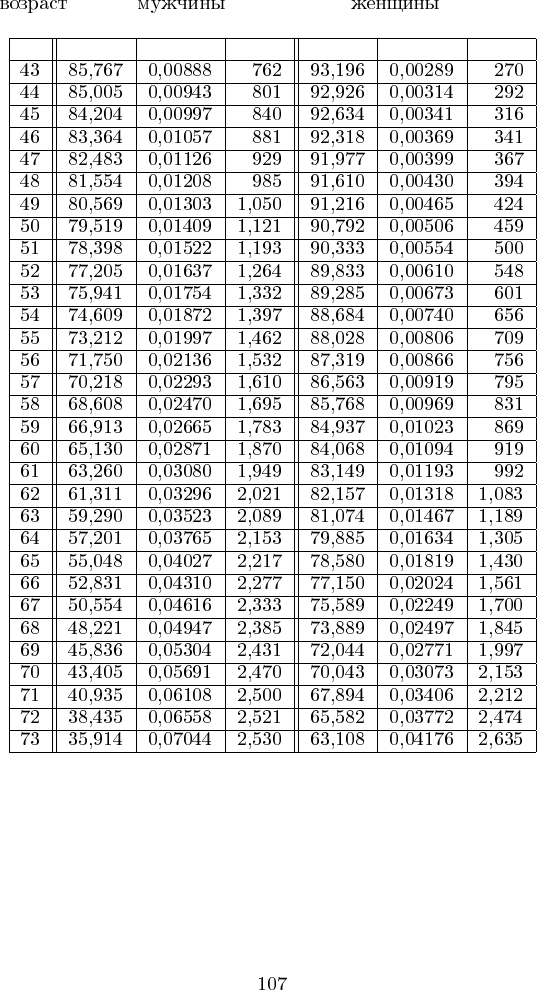
x l
x
q
x
d
x
l
x
q
x
d
x
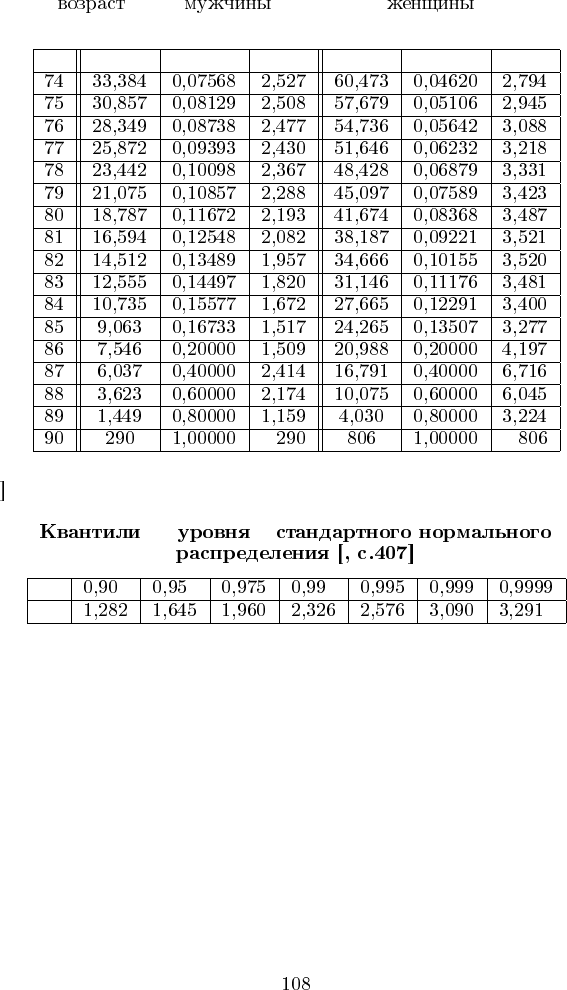
x l
x
q
x
d
x
l
x
q
x
d
x
x
p
p
p
x
p
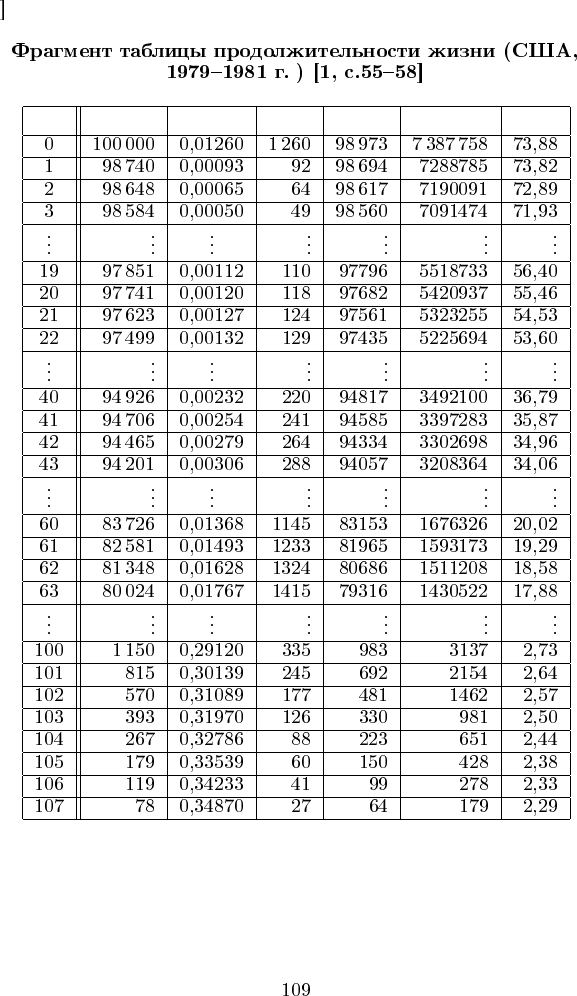
x l
x
q
x
d
x
L
x
T
x
◦
e
x

f(x) x = x
0
∈ X
f
(n)
(x
0
), x = x
0
f
0
(x), f
00
(x), . . . , f
(n−2)
(x),
x = x
0
, f
(n−1)
(x),
x = x
0
.
f(x) n x = x
0
,
f(x) = f(x
0
) +
f
0
(x
0
)
1!
(x − x
0
) + . . . +
f
(n)
(x
0
)
n!
(x − x
0
)
n
+ o((x − x
0
)
n
),
x → x
0
.
f(x)
x
0
n + 1, x
f(x) = f(x
0
) +
f
0
(x
0
)
1!
(x − x
0
) + . . . +
f
(n)
(x
0
)
n!
(x − x
0
)
n
+
+
f
(n+1)
(x
0
+ θ(x − x
0
))
(n + 1)!
(x − x
0
)
n
, 0 < θ < 1.
f
n
(x) ϕ(x)
A, n x ∈ A
|f
n
(x)| ≤ ϕ(x)
lim
n→∞
f
n
(x) = f(x) x ∈ A.
Z
A
|f(x)|dx < ∞,
lim
n→∞
Z
A
f
n
(x)dx =
Z
A
f(x)dx,
lim
n→∞
Z
A
|f
n
(x) − f (x)|dx = 0.
η, ξ
1
, ξ
2
, . . .
|ξ
n
| ≤ η, Eη < ∞ ξ
n
→ ξ
Eξ < ∞,
Eξ
n
→ Eξ,
