Корнилов И.А. Элементы страховой математики
Подождите немного. Документ загружается.

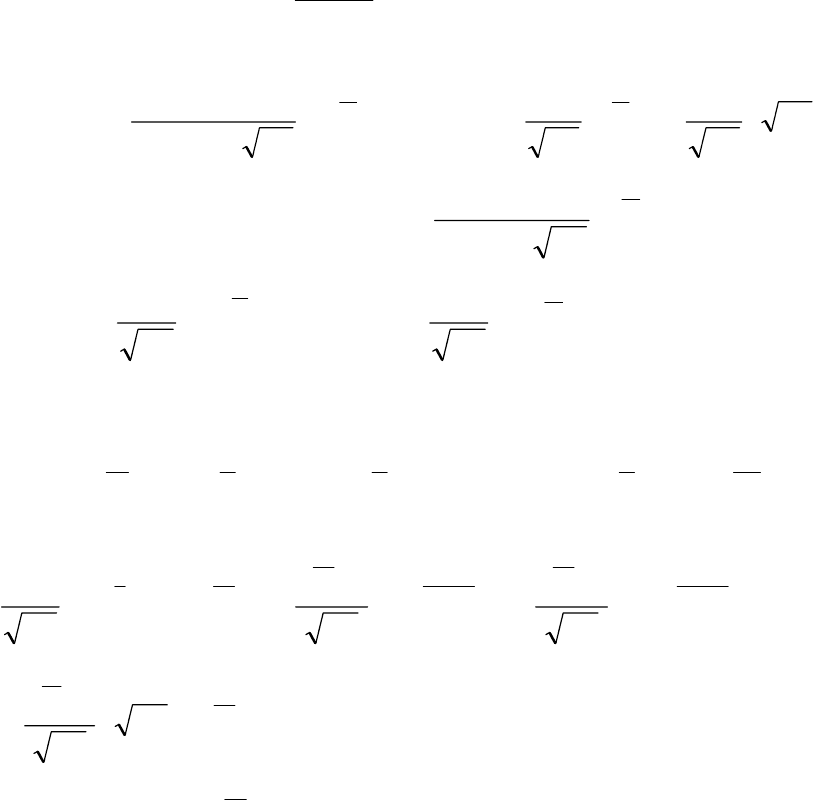
291
∫
∞
=
0
1f(x)dx
Сделаем замену:
t
σ
mlnx
=
−
;
mtσlnx
+
=
;
mtσ
ex
+
=
Тогда:
(
)
σdtem)d(tσeeddx
mtσmtσmtσ +++
=+⋅==
()
12π
2π
1
dte
2π
1
σdtee
2πσe
1
f(x)dx
2
t
mtσ
2
t
mtσ
0
22
=⋅==⋅⋅
⋅
=
∫∫∫
∞
∞−
−
∞
∞−
+
−
+
∞
()
()
dte
2π
e
dteee
2π
1
dtee
2πσe
1
exf(x)dxM(X)
tσ
2
t
m
mtσ
mtσ
2
t
mtσ
mtσ
0
2
2
2
t
2
∫∫
∫∫
∞
∞−
+−
∞
∞−
∞
∞−
+
−
+
+
∞
=⋅⋅⋅=
===
−
Для удобства показатель надо дополнить до «полного квадрата».
[][]
()
2
σ
σt
2
1
σσ2tσt
2
1
2tσt
2
1
tσ
2
t
2
2
2222
2
+−−=−+−−=−−=+−
Тогда искомый интеграл превратится :
() ()
()
m
2
σ
m
2
e
2
σt
m
2
σ
2
σt
m
2
σ
2
σ
σ)(t
2
1
m
2
2
2
2
2
2
2
2
e2π
2π
e
σtde
2π
e
dte
2π
e
dtee
2π
e
+
+
∞
∞−
−
−
+
∞
∞−
−
−
+
∞
∞−
−−
=⋅=
=−⋅==⋅
∫∫∫
т.е
m
2
σ
2
eM(X)
+
=
Итак, формула начальных моментов
M(X
k
) справедлива для К=1.
Это позволяет убедиться в её правильности для произвольного «
К»
методом индукции. Тогда используя
()
2m2σ2
2
eXM
+
=
получаем выражение для D(X).
2. СВОЙСТВА ПРОИЗВЕДЕНИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН
Для двух независимых случайных величин U и V строим новую
величину
VUW ⋅=
. Тогда

292
22
2222
2222
2222
2222222
2222
M(U)D(V)M(V)D(U)D(V)D(U)D(W)
[M(V)][M(U)][M(U)]D(V)[M(V)]D(U)
D(V)D(U)](M(V))[D(V)](M(U))[D(U)]M[V]M[U
[M(U)]D(U)]M[U,[M(U)]]M[UD(U)
[M(V)][M(U)]M[V]]M[UM(V)][M(U)]VM[U
M(V)][M(U)]V)M[(UV)][M(U]V)M[(UV)D(UD(W)
M(V)M(U)V)M(UM(W)
⋅+⋅+⋅=
⋅+⋅+⋅+
+⋅=+⋅+=⋅
+=−=
⋅−⋅=⋅−⋅=
=⋅−⋅=⋅−⋅=⋅=
⋅=⋅=
−=
==
p1q0,
p1,
AV
U = (X|A)
Например,
А – случайное страховое событие, Х – случайная
величина ущерба (безусловного или полного), (
Х|A) - случайная
величина ущерба,
если страховой случай произошел.
3. СВЁРТКА (КОМПОЗИЦИЯ ДВУХ СЛУЧАЙНЫХ ВЕЛИЧИН)
Пусть известны плотности двух CB: X и Y. Надо найти плотность
CB:
Z=X+Y
X ~ f(x) , Y ~ g(y)
Z = X+Y h(z) = ? H(z) = ?
∫
−⋅=−<∧<=<+=<=
Z
0
x)dxg(zf(x)x)}z(Yx)P{(Xz}YP{Xz}P{ZH(z)
тогда:
h(z) = H'(z)
YXZ )(e~Y )(e~X
n!
µ
-µ
m!
λ
λ
n
m
+=⋅⋅
−
Для дискретных величин интеграл заменяется суммой
Например, есть две СВ, распределённые по законам Пуассона:

293
∑
∑∑
∑
∑
∑
∑∑
∑
∑
=
µ+λ
µ+λ−
µ+λ⋅µ+λ⋅
−
==
+⋅
−
−⋅
+⋅
=
−
+−
=
−
+−
=
−⋅
⋅
+−
=
−⋅
⋅
+−
=
−⋅
⋅
+−
−
−
=
−
=
⋅=⋅=⋅=
=⋅⋅=⋅⋅
⋅=⋅⋅+⋅=
=⋅+⋅=
=⋅+⋅=
=⋅=⋅=
=⋅⋅⋅=
=−=⋅===
µ+λ−µ+λ−
+−
+−−
−
−
++
−−
−
k
0m
!k
)(
)(
!k
)(e
m
!k
)(e
kk)(k)(
e1)k(P
mkm
k
0m
k
0m
m
k
k!
µ)(λe
mkm
m)!(km!
k!
k!
µ)(λe
k
0m
k!
k!
m)!(km!
qp
kµ)(λ
k
0m
m)!(km!
qp
kµ)(λ
k
0m
m)!(km!
][][
kµ)(λ
k
0m
m)!(km!
µλ
µ)(λ
k
0m
m)!(km!
µλ
µ)(λ
m)!(k
µ
µ
k
0m
m!
λ
λ
k
0m
qpCqp
µ)(λe
µ)(λe
µ)(λe
e][e
)](e)[(e
m)kP(Ym)P(X k)P(Z
kµ)(λ
kµ)(λmkm
mkm
mk
µ)(λ
µ
m
µ)(λ
λ
mkmmkm
mk
m
т.е. формула Пуассона для параметра (
λ+µ). Интенсивности потоков
складываются.
Для нормального закона выполняется то же условие.
Свёртка двух независимых нормальных СВ образует нормальную
СВ с параметрами
(µ
x
+µ
y
), (σ
2
x
+σ
2
y
).
4. КОМПОЗИЦИЯ НЕСКОЛЬКИХ РАВНОМЕРНО
РАСПРЕДЕЛЕННЫХ СЛУЧАЙНЫХ ВЕЛИЧИН
Сначала без потери общности рассмотрим СВ, равномерно
распределенное на
[0,а]. Их плотность 1/а на этом отрезке и 0 вне его.
Итак
{
}
0иначе α;,0a(x)U
-1
1
≤=
Рассмотрим две случайные величины
Х и Y. Z=X+Y Є [0, 2а]
()
∫∫∫
+=−⋅=
a
0
2a
a
21212
2a
0
1
dxffdxffx)dx(zf(x)fzf
1)
0<z<a тогда
α
1
x)(zf ,
α
1
(x)f
21
=−=
т.е.
2
z
0
z
0
2
21
α
z
α
1
dxff
==
∫

294
2)
a<z<2a Здесь необходимо выполнение двух условий:
0<x<a тогда
a
xf
1
)(
1
=
и
0<z-x<a (т.е.x>z-a) тогда
a
xzf
1
)(
2
=−
Итак:
2
αz
α
2
e
αz
21
α
z)(2α
x
α
1
dxff
−
==
−
−
∫
Окончательно:
<<
<<
=
иначе 0,
2αzα ,
α
z-2α
α,z0 ,
α
z
f(z)
2
2
В наших обозначениях:
<<−
<<⋅
−
−
иначе
axaxaa
axxa
xU
,0
2),2(
0,
)(
2
2
2
Для произвольного “
n” получим по индукции
[]
a)(xU(x)U
a
1
y)dy(xU
a
1
(x)U
nn
a
0
n1n
−−=−=
∫
+
Эти результаты обобщаются на произвольном отрезке [
a,b].
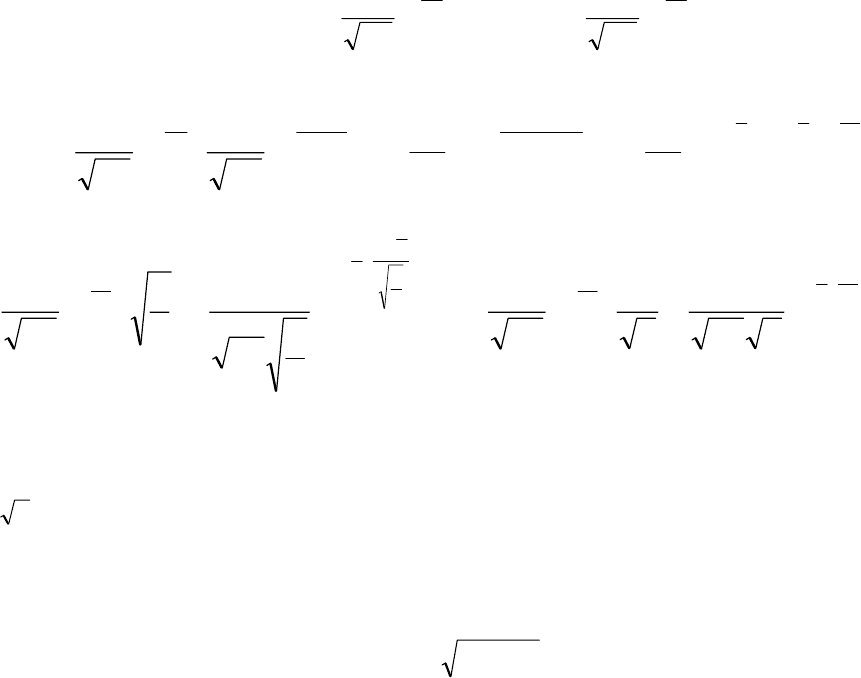
295
5. КОМПОЗИЦИЯ ДВУХ ОДНОМЕРНЫХ НОРМАЛЬНЫХ СВ
Без потери общности проведем доказательство для
нормированных нормальных СВ.
2
y
2
2
x
1
2
2
e
2π
1
(y)f~y,e
2π
1
(x)f~x
−−
==
z=x+y
−
−
∞
∞−
−
−
−
∞
∞−
+
−−
∞
∞−
−+
−
−
−
∞
∞−
−
=⋅=⋅⋅⋅=
===⋅=
∫
∫∫∫
2
z
2
1
4
z
2
1
2
z
x
2
1
4
z
4
z
2
z
x2
2
1
2
x)(zx
2
x)(z
2
x
2
2
2
2
2
2
2222
e
22π
1
2
1
e
2π
1
dxe
2
1
2π
1
2
1
e
2π
1
dxe
2π
1
dxe
2π
1
dxe
2π
1
e
2π
1
f(z)
Это плотность нормального закона распределения с параметрами
0
и
2
.
Обобщая получим:
)σ,N(µ~Y),σ,N(µ~X
2211
, то Z=X+Y
)σσ;µN(µ~Z
2
2
2
121
++
Т.е. сумма независимых нормально распределенных СВ имеет
нормальное распределение.
В дальнейшем это положение будет обобщено и на случайных
многомерных СВ.
6. КОМПОЗИЦИЯ НОРМАЛЬНЫХ ЗАКОНОВ НА ПЛОСКОСТИ
Если есть две независимые величины
X и Y, то для случайной
величины
Z=X+Y справедливо: M(Z)=M(X)+M(Y); D(Z)=D(X)+D(Y).
В многомерном случае недостаточно определить только
характеристики каждого признака в отдельности. Необходимо учесть и
взаимосвязь признаков. Например, для двух независимых двумерных
случайных величин
V
1
(X
1
,Y
1
) и V
2
(X
2
,Y
2
), каждая из которых
распределена нормально, необходимо задать наборы параметров:
{mx
1
, my
1
, σx
1
, σy
1
, px
1
y
1
} и {mx
2
, my
2
, σx
2
, σy
2
, px
2
y
2
}
Теперь проанализируем V=V
1
+V
2
. Для составляющих этой новой
вершины справедливо:
X=X
1
+X
2
и Y=Y
1
+Y
2
.
Следовательно:
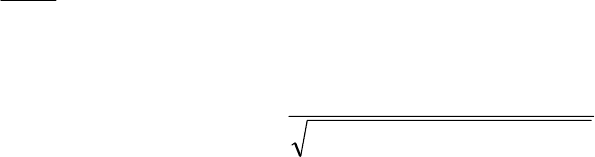
296
2121
2121
y
2
y
2
y
2
x
2
x
2
x
2
yyyxxx
σσσ;σσσ
;mmm;mmm
+=+=
+
=
+
=
А взаимосвязь признаков характеризуется корреляционным
моментом.
K(X,Y), для которого справедливо:
KKK
2211
yxyxxy
+
=
Т.к.
yx
xy
xy
σσ
K
ρ =
, то
2
y
σσρσσρσσρ
2221111
xyxyxyxyxxy
+
=
поэтому:
()()
2121
22221111
y
2
y
2
x
2
x
2
yxyxyxyx
xy
σσσσ
σσρσσρ
ρ
+⋅+
⋅
+
⋅
=
Эти формулы позволяют выполнить композиции нормальных
законов на плоскости. Теперь можно присоединить третью СВ
V
3
(X
3
,Y
3
)
и т.д. Если использовать трехмерные нормальные СВ, то необходимо
использовать матрицу
R и формулы в матричном виде.
7. ПРОИЗВОДЯЩАЯ ФУНКЦИЯ. ЕЁ СВОЙСТВА И
ИСПОЛЬЗОВАНИЕ.
Рассмотрим пример:
СВ
X принимает значения: 0,1,2,3,… с вероятностями p
i
, т.е.
P{x=i}=p
i
, P{x>i}=q
i
, i=0,1….
Тогда : q
k
=p
k+1
+p
k+2
+…, k≥0
Производящие функции для последовательностей {
p
i
} и {q
i
} это:
P(S)=p
0
+p
1
S+p
2
S
2
+p
3
S
3
+….
Q(S)=q
0
+q
0
S+q
2
S
2
+q
3
S
3
+…
Оба ряда сходятся при S<1
Производная
1
1
)('
−
∞
=
⋅⋅=
∑
k
k
k
SpkSp
тоже сходится при S<1
Если
S=1, то ∑kp
k
=M(X)
Разумеется, интерес представляет, в основном, КОНЕЧНОЕ
математическое ожидание.
Тогда:
Q(1)=P' (1)=M(X), т.е.
∑∑
∞∞
=⋅=
01
)(
kj
qpjXM
Отсюда следует, что M[X(X-1)]= ∑k(k-1)p
k
=P'' (1)=2Q' (1)
И поскольку:
D(X)=M(X
2
)-(M(X))
2
, то
D(X)=P' ' (1)+P' (1)-(P' (1))
2
=Q' (1)+Q(1)-Q
2
(1)
Это позволяет вычислять математическое ожидание и дисперсию
Х, используя производящие функции P и ее производные: P’, P’’ в точке
S=1.
297
8. КОМПОЗИЦИЯ СЛУЧАЙНЫХ ВЕЛИЧИН.
СВЁРТКИ И ПРОИЗВОДЯЩИЕ ФУНКЦИИ.
Пусть
X~f(x), Y~g(y); Z=X+Y. Исследователя интересует:
h(z)=H’(z);
где
H(z) = P(Z<z) = P(X+Y<z) = P((X<x) и (Y<y)) = f(x)g(z-x)dx
Для независимых CB (
X и Y) независимы и S
х
и S
y
, поэтому:
M(S
x+y
)=M(S
x
)M(S
y
)
В ряде случаев это позволяет упростить процесс композиции
случайных величин. В общем случае используется таблица
производящих функций для основных распределений (аналогично
таблицам производных, интегралов, рядов и т.д), что и упрощает
процесс аналитических выкладок. Проиллюстрируем на некоторых
примерах применение этого аппарата.
А. Биноминальное распределение :
Производящая функция для
knkk
n
qpCpnkb
−
=),;( есть
nknk
n
k
k
n
psqqpsC )()(
0
+=⋅
−
=
∑
, т.е. b(k;n;p) – распределение суммы
∑
=
n
in
XS
1
независимых CB с производящими функциями: q+ps
т.е.
{b(k ;n, p)}={b(k;1,p)}
n*
(n-кратная свертка).
В частности, из мультипликативного свойства следует:
{b(k;m;p)}∗{b(k;n;p)}={b(k;m+n;p)}
Очевидно, что дифференцируя производящую функцию, получим:
M(Sn)=np и D(Sn)=npq
Для доказательства найдем первую и вторую производные:
d(q+pS)
n
/dS = np(q+pS)
n-1
;
d
2
((q+pS)
n
)/dS
2
= n(n-1)p
2
(q+pS)
n-2
.
Подставляя S=1 и используя выражение для M(X), D(X), получим:
D = n(n-1)p
2
+ np – (np)
2
= npq.
Разумеется, для столь простого случая удобнее получить эти
результаты на основе свойств математического ожидания и дисперсии
суммы
n независимых одинаково распределенных случайных величин,
но в более сложных ситуациях данный подход эффективнее
традиционного.
(q+pS)
n
(q+pS)
m
= (q+pS)
m+n

298
т.е. сумма двух биномиально распределенных случайных величин также
подчиняется биномиальному распределению. Непосредственное
доказательство этого свойства – более трудоемко!
Б. Распределение Пуассона.
Производящая функция распределения Пуассона
!
);(
k
ekp
k
λ
λ
λ
⋅=
−
равна:
()
∑
∞
=
−+−−
==
0
)1(
!
k
SS
k
ee
k
S
e
λλλλ
λ
Отсюда:
{p(k;λ)}∗{p(k;µ)}={p(k;λ+µ)}
т.к.
exp(λ(S-1))* exp(m(S-1))= exp((λ+m)(S-1))
Полезно сравнить мультипликативное свойство с
непосредственным выводом. Объединение двух потоков Пуассона
является потоком Пуассона. Это полезное свойство активно
используется в актуарных расчетах.
При дифференцировании убеждаемся, что
M(k)=D(k)=λ
Например,
d(exp(λ(S-1)))/dS = λexp(λ(S-1));
d
2
(exp(λ(S-1)))/dS
2
= λ
2
exp(λ(S-1));
Подставим: S=1 и получим результат.
В. Геометрическое и отрицательное биномиальное распределение.
Геометрическое: Х: p{x=k}=q
k
p, k=0,1,2……; p+q=1
Тогда производящая функция :
qs
p
qsp
k
k
−
=
∑
∞
=
1
)(
0
d(p/(1-qS))/dS = pq/(1-qS)
2
; d
2
(p/(1-qS))/dS
2
= 2pq
2
/(1-qS)
3
;
Подставив:
S=1 и используя выражения для M(X), D(X), получим:
M(X)=pq/(1-q)
2
=q/p; D(X)= 2pq
2
/(1-q)
3
+q/p –(q/p)
2
= (q
2
+pq)/p
2
;
Отсюда:
p
q
xM =)(
и
2
)(
p
q
xD =
.
Здесь
Х можно интерпретировать, как время ожидания ПЕРВОГО
успеха (среди
n испытаний).
Для
отрицательного биномиального распределения
kr
r
k
qpprkf
C
)();;( −=
−
k=0,1,2…. P{S
r
=k}=f(k;r;p)

299
Число неудач, предшествующих
r-му успеху. Т.е. это r-кратная
свертка геометрического распределения
{f(k;r;p)}={q
k
p}
r*
Тогда производящая функция:
r
qs
p
−
)1(
При
r>0: M(X)=rq / p; D(X)= rq / p
2
Доказательство:
F = (p/(1-qS))
r
;
dF/dS = p
r
*d((1-qS)
-r
)/dS = p
-r
(1-qS)
–r-1
(-q) =
= (p/(1-qS))
r
rq/(1-qS) = F rq/(1-qS);
d
2
F/dS
2
= d(dF/dS)/dS = d(F* rq/(1-qS))/dS =
= dF/dS* rq/(1-qS) + F*d( rq/(1-qS))/dS =
= F* rq/(1-qS)* rq/(1-qS) + F* rq/(1-qS)
2
(-1)(-q) =
= F*( rq/(1-qS)
2
+ rq
2
/(1-qS)
2
) = F* rq
2
*(1+r)/ (1-qS)
2
;
Подставив:
S=1 и используя выражения для M(X), D(X), получим:
M(X) = p
r
/(1-q)
r
rq/(1-q) = rq/p;
D(X) = (p/(1-q))
r
rq
2
(1+r)/(1-q)
2
+ rq/p – (rq/p)
2
= rq
2
(1+r)/p
2
+ rq/p
– (rq/p)
2
=
= (rq
2
+r
2
q
2
+ rpq – r
2
q
2
)/p
2
= (rq
2
+ rpq) /p
2
= rq/p
2
;
Кроме того:
{f(k;r
1
;p)}∗{f(k;r
2
;p)}={f(k;r
1
+r
2
;p)}
Т.е. и для этого распределения сумма двух СВ подчиняется тому же
закону.
Г: Свойства свертки:
g∗f=f∗g ;
(f∗g)∗h=f∗(g∗h) ;
f
∗(g+h)=f∗g+f∗h.
Эти свойства иногда позволяют упростить аналитические
выкладки.
9. ПОЛУЧЕНИЕ ТОЧЕЧНЫХ ОЦЕНОК
МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Пусть есть случайная величина
Х, относительно которой
предполагается, что она распределена по некоторому закону: f(x,O), где
О – вектор параметров. Значения этих параметров – неизвестны, их надо
определить на основании n наблюдений СВ, т.е.
Хi, I=1…n.
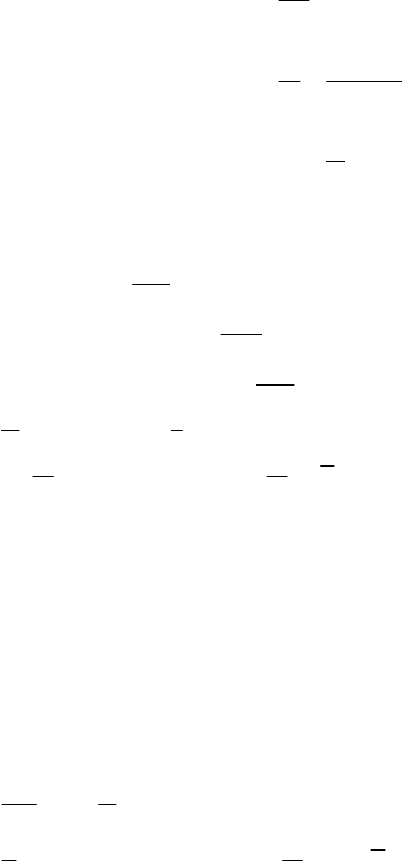
300
Для этого строится произведение
f(Xi, O), которое при
логарифмировании превращается в сумму
ln f(Xi,O). Экстремум этой
суммы находится приравниванием к нулю частных производных по
каждому неизвестному параметру. Возникает система уравнений
относительно неизвестных параметров. Решение этой системы
указывает оценки искомых параметров, оптимальные с точки зрения
метода максимального правдоподобия.
А. Оценка максимального правдоподобия в биноминальном
законе.
В “
n” опытах событие реализовалось ”r” раз.
n
r
p
0
p)(1
z)(n
p
r
0lnL
p
p)r)ln(1(nrlnplnClnL
p)(1pCL
r
n
rnrr
n
=
=
−
−
−
=
∂
∂
−−++=
−=
∧
−
Б. Оценка максимального правдоподобия в законе Пуассона.
n ..., 1,i ; e)f(x
)!(x
λ
λ
i
i
i
x
=⋅=
−
∏∏
⋅=
−
)!(x
λ
λ
i
i
i
x
e)f(x
)!ln[(xln(λn)x(λ)(]ln[e)f(xln
ii
)!(x
λ
λ
i
i
i
x
∑
∑
∑
∑
∏
−⋅+−=⋅=
−
00xn
λ
1
i
λ
=−⋅+−=
∑
∂
∂
xλ0 n
n
x
λ
x
ii
===−
∑∑
)
В. Нахождение оценки параметра α для экспоненциального закона
по методу максимального правдоподобия
i
αx
i
αe)f(x
−
=
∑
⋅==
−
−
∏∏
i
i
xα
n
αx
i
eααe)f(x
∑
∏
−=
∑
+=
−
i
xα
n
i
xanlnαlnelnα)f(xn
i
l
0
1
ln
=−⋅=
∑
∂
∂
i
xn
αα
()
(
)
1
1
n
x
i
n
x 0x
i
−
−
α
==α=−
∑∑
)
