Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering

Подождите немного. Документ загружается.

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

∑

N,k

∑

L (

)(x

)L (

)(x

∑

f (x

)L (

)(x

∀

, j = 1, ...,N . (98)

Here x

denote the Gauss-Lobatto points and w

the Gauss-Lobatto weights deﬁned

by (36) and (40), respectively. Note that in the multi-dimensional case x

is a vector,

is a tensor product and w

is the product of the Gauss-Lobatto weights in each

direction separately. We now deﬁne in each element the matrix A





= L (

)(x

) , (99)

i.e. the matrix coefﬁcient denotes the application of the differential operator to the

basis function evaluated at the p

Gauss-Lobatto point. Furthermore we introduce

the diagonal weight matrix W





= w

. (100)

The discretized least-squares problem (98) can then be written as

∑









N,k

∑









, (101)

where the vector F contains the elements (F)

= f (x

). The system of algebraic

equations obtained in this way, i.e. using variational analysis, is called the normal

equations. The normal equations reﬂect on a discrete level the symmetry that was

already mentioned at the continuous level. Note that Gauss-Lobatto integration may

be performed on a ﬁner grid than the grid on which the unknowns are deﬁned. In

this case the matrix A

is non-square, i.e. there are more rows than columns in the

matrix. The resulting normal equations, however, deliver a square, positive deﬁnite

matrix which possesses a unique solution.

7.2.2 Direct Minimization - LSQSEM-DM

In order to avoid variational analysis we start with the original minimization prob-

lem.

Find u ∈ X(

Ω

) which minimizes I (u) =

kL u − f k

Ω

)

. (102)

Since we decompose the computational domain

Ω

into a union of non-overlapping

sub-domains

Ω

, k = 1,.. .,K, we can also write this as

Find all u

∈ X(

Ω

) which minimize the functional

213

Marc Gerritsma and Bart De Maerschalck

I (u

,.. .,u

) =

∑

k=1



L u

− f



Ω

)

. (103)

Now in each domain

Ω

we are going to restrict our search to a ﬁnite-dimensional

subspace X

(

Ω

) ⊂ X(

Ω

) using the spectral approximation given by (38)

Find all u

N,k

∈ X

(

Ω

) which minimize the functional

I (u

N,1

,.. .,u

N,K

) =

∑

k=1



L u

N,k

− f



Ω

)

. (104)

Next we introduce numerical quadrature to evaluate the integrals which constitute

the L

-norm. This gives

Find all u

N,k

∈ X

(

Ω

) which minimize the functional

I (u

N,1

,.. .,u

N,K

) ≈

int

∑

p=0

∑

k=1



L u

N,k

− f





, (105)

where N

int

denotes the number of integration points in element k. Introducing our

matrix notation (99) and (100) this can be written as

Find all u

N,k

∈ X

(

Ω

) which minimize the functional

∑

k=1



N,k

−F





N,k

−F



∑

k=1



N,k

−F



. (106)

So the procedure of domain decomposition, insertion of an approximate solution

and the use of numerical integration has converted the minimization in the func-

tion space L

(

Ω

) to a minimization problem in Euclidean space: Find the ﬁnite-

dimensional vector ﬁelds u = (u

,.. .,u

)

∈ R

such that the norm in R

given

by (106) is minimized. If m = n, i.e. the number of unknowns in the global system

equals the number of equations, the use of the weight matrix W

is then inconse-

quential and the problem reduces to a collocation method evaluated in the Gauss-

Lobatto-Legendre points, [42, 43, 44], given by

∑

k=1



N,k

−F



= 0 . (107)

In case m > n, we have more equations than unknowns and the solution which

minimizes the residual norm of the overdetermined system is then given by

∑

k=1

∑

k=1

. (108)

214

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

Let us for convenience introduce the following notation B =

∑

k=1

√

and G =

∑

k=1

√

. Then we have the following Theorem, [5, 6]:

Theorem 2. Let B ∈ R

m,n

and G ∈R

, then the following 2 statements are equiva-

lent:

• Determine the vector u ∈ R

which minimizes the Euclidean norm kBu−Gk

;

• Determine the vector u ∈ R

such that the residual R = G −Bu ∈N





⊓⊔

See [49] for the proof.

The above Theorem shows that ﬁnding the minimizer of the overdetermined sys-

tem (108) is equal to imposing

∑

k=1



−F



= 0

⇐⇒ (109)

∑

k=1









u =

∑

k=1





which is the same equation that we obtained using variational analysis. Therefore,

direct minimization given by (108) is equivalent to (101) as a result of the Theorem.

However note that (108) is more appealing to use than (101). Since no pre-

multiplication is employed we do not lose the sparsity pattern of the matrix A

and

we prevent ﬁll-in in the global matrix. Bear in mind that W

is a diagonal matrix

and so is its square root. Pre-multiplication with a diagonal matrix amounts to row-

scaling which does not affect the sparsity.

7.2.3 Global QR

Let us return to our global system of algebraic equation given by

Bu = G ⇐⇒ Find u which minimizes kBu −Gk

, (110)

where B ∈R

m,n

, u ∈R

and G ∈R

. Now for any orthogonal matrix Q ∈ R

m,m

have

kQ(Bu −G)k

= kBu −Gk

, (111)

since the Euclidean norm is invariant under orthogonal transformations.

We now decompose the m ×n matrix B in a QR-decomposition, B = QR, where

Q is an orthogonal m ×m-matrix and R is an m ×n upper-triangular matrix. The R

matrix can be written as

R =





, (112)

215

Marc Gerritsma and Bart De Maerschalck

where

R is an upper-triangular n×n matrix with non-zero diagonal entries, and 0 is

an (m −n) ×n matrix with zero entries.

With this decomposition we have

kBu −Gk

= kQ

(Bu −G)k

= kRu −Q







u −







= k

Ru −c

+ kc

, (113)

where c

is an n-vector and c

is an m−n-vector. With this decomposition, minimiz-

ing the Euclidean norm is straightforward. The second term, kc

, in (113) cannot

be minimized. The only terms that can be made small – zero in fact – is the ﬁrst

term on the right hand side of (113). So we have for the least-squares solution

−1

, (114)

which is just a back-substitution for the upper-triangular matrix

R. An approxima-

tion to the L

-norm of the residual is given by the second term, kc

, and this

value is available without solving for u

. This may be advantageous in hp-adaptive

schemes.

Note again, that when exact arithmetic is used the minimizer u

is equal to the

least-squares solution obtained by the conventional least-squares formulation which

is obtained by applying variational analysis and solving the normal equations. This

algorithm can be improved when one observes that it is not necessary to compute

the matrix Q to solve the over-determined system directly.

With a suitable global node numbering this algorithm can be converted into a

block-QR algorithm. See [49] for further particulars.

7.2.4 The Poisson equation

In this section a sample problem is presented which consists of a modiﬁed Poisson

equation given by

κ∆φ

= f(x,y) , (x, y) ∈ [−1,1]

, (115)

where

f (x,y) = −2

sinxsiny . (116)

The solution in this case is obviously independent of the parameter

, but the con-

dition number of the resulting system will strongly depend on

In order to apply the least-squares formulation which allows for a C

ﬁnite ele-

ment approximation, the governing equation needs to be rewritten as an equivalent

ﬁrst order system

u −∇

= 0 , (117)

216

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

∇·u = f . (118)

Note that there are other equivalent ﬁrst order systems possible with improved sta-

bility estimates, but this model problem is only introduced to compare formulations.

Following Jiang, [51], it is easy to show that this problem is well-posed



(

Ω

)

+ kuk

div;

Ω

)



≤ ku−∇

(

Ω

)

+ k

∇·uk

(

Ω

)

≤ k

(

Ω

)

+ kuk

div;

Ω

)

, (119)

for

≤ 1. So the coercivity constant scales with

and therefore the condition

number is proportional to

−2

. We therefore expect to see differences between the

conventional least-squares formulation and direct minimization as proposed in this

section for

≪ 1. For

= O(1), however, both formulations are expected to give

similar results. In order to assess the improved stability of direct minimization the

artiﬁcially ill-conditioned system is solved on a 5 ×5 grid with polynomial degree

N = 5.

-1

-0.5

0.5

phi

-3

-2

-1

-3

-2

-1

X Y

-1

-0.5

0.5

phi

-3

-2

-1

-3

-2

-1

X Y

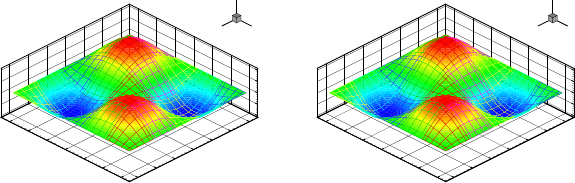
Fig. 24 Solution for

= 1 obtained by the conventional least-squares formulation (left) and the

result obtained by direct minimization (right)

Figure 24 (left) shows a plot of the solution of the Poisson equation obtained by

the conventional least-squares formulation with

= 1. Figure 24 (right) gives the

solution obtained by Direct Minimization for

= 1. The results are indistinguish-

able. This follows from the observation that both methods are equivalent if exact

arithmetic is used.

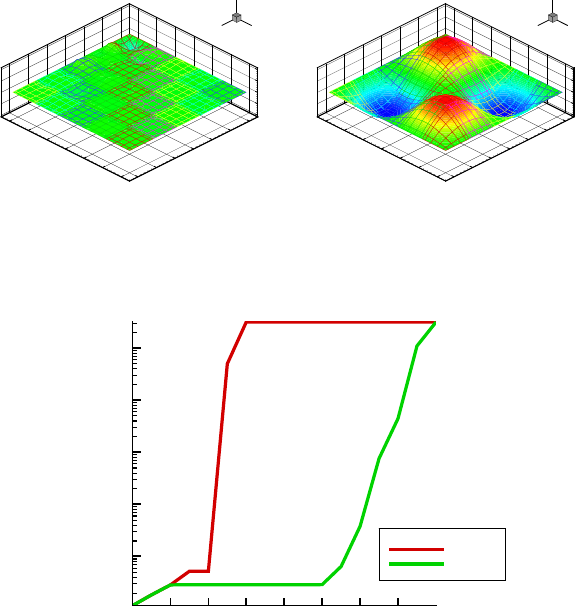
In Figure 25 results for the case

= 10

−5

are presented, where the differences

between the conventional least-squares formulation and direct minimization become

apparent. The conventional least-squares formulation is unable to approximate the

exact solution sufﬁciently accurate due to the loss of precision, whereas Direct Min-

imization still approximates the solution sufﬁciently accurate.

The L

-error for both the conventional least-squares formulation and Direct Min-

imization versus the parameter

is depicted in Figure 26. The conventional least-

squares formulation (red line) approximates the solution rather well for a

up to

−4

after which the error grows dramatically. Direct Minimization is capable of

217

Marc Gerritsma and Bart De Maerschalck

-1

-0.5

0.5

phi

-3

-2

-1

-3

-2

-1

X Y

-1

-0.5

0.5

phi

-3

-2

-1

-3

-2

-1

X Y

Fig. 25 Solution for

= 10

−5

obtained by the conventional least-squares formulation (left) and

the result obtained by direct minimization (right)

-14

-12

-10

-8

-6

-4

-2

-4

-3

-2

-1

||e||

LS DM

L2 error norm of the Poisson problem on a 25 element mesh,

polynomial degree 5

Fig. 26 The L

-error of the conventional least-squares solution (red) and the solution obtained by

direct minimization (green)

approximating the solution up to a

of O(10

−11

). Note that the solution is indepen-

dent of

Table 5 shows the condition number of the conventional least-squares and Direct

Minimization approach versus polynomial degree in the spectral element method.

One observes that the condition number of Direct Minimization is approximately the

square root of the condition number associated with the conventional least-squares

formulation.

218

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

Condition number

N DM LS

2 5.934 35.215

3 11.914 142.056

4 20.228 409.369

5 30.646 936.737

Table 5 Comparison of the condition numbers obtained from Direct Minimization (DM) and the

conventional least-squares method (LS) as a function of the polynomial degree

Condition number

P = 2 P = 4

K DM LS DM LS

4 4.430 19.635 13.394 197.635

9 5.935 35.222 20.230 409.635

16 7.688 59.111 27.060 732.635

25 9.534 90.891 33.879 1147.786

Table 6 Condition number as a function of the number of elements for Direct Minimization (DM)

and the conventional least-squares method (LS)

Table 6 shows the growth of the condition number as a function of the num-

ber of elements for two polynomial degrees. One observes that, especially for high

order methods which employ much higher polynomial degrees than N = 4, the dif-

ference in condition number between the conventional least-squares method and

Direct Minimization grows very fast.

7.3 Application of LSQSEM to viscoelastic ﬂuids

Inspired by the success of the simulation of a Newtonian ﬂow around cylinders

attempts were undertaken to solve the ﬂow of a viscoelastic ﬂuid around a cylinder

in a channel. The model that was used was the so called Upper-Convected Maxwell

(UCM) model. The UCM model is not the most realistic model for viscoelastic

ﬂows, but it is the simplest one in terms of number of physical parameters. However,

this model is very hard to solve numerically due to its conditional well-posedness,

see for instance [35, 39], and therefore is a very good test problem for numerical

schemes.

This problem was solved using a discontinuous least-squares formulation, [36].

Furthermore, Direct Minimization was used, see Subsection 7.2.

The Upper Convected Maxwell model is given by conservation of mass for an

incompressible ﬂow

∇·u = 0 in

Ω

, (120)

where u denotes the velocity vector ﬁeld.

219

Marc Gerritsma and Bart De Maerschalck

Conservation of momentum in the Stokes limit yields

∇·(pI −

) = 0 in

Ω

, (121)

where p denotes the pressure ﬁeld, I the unit tensor in R

, d = dim(

Ω

) and

is the

extra-stress tensor.

The constitutive equation which relates the extra-stress tensor to the velocity ﬁeld

is given by

∇

= 2

d , (122)

where

is the relaxation time and

the polymeric viscosity of the ﬂuid,

∇

· denotes

the upper convected derivative deﬁned as

∇

A =

∂

+ (u,∇) A −L

−

, (123)

where (L)

i j

∂

and 2d = L + L

. The UCM model (122) describes the fact

that the extra-stress does not instantaneously equal the rate of deformation of the

ﬂow, but is also convected and deformed along the particle paths as expressed by

(123). When the relaxation time

= 0, the stress components are no longer con-

vected along the particle paths and Newtonian Stokes ﬂow is retrieved.

Consider the ﬂow past a cylinder placed at the centerline of a channel of width

4R, where R denotes the radius of the cylinder. The computational domain equals

the domain used by Alves, Pinho and Oliveira, [2]. At inﬂow, 19R upstream of the

cylinder, a fully developed Poiseuille ﬂow is prescribed for velocity and extra-stress

components. The downstream length is taken to be 59R. The number of spectral

elements equals K = 16 and the polynomial degree in each element has been set

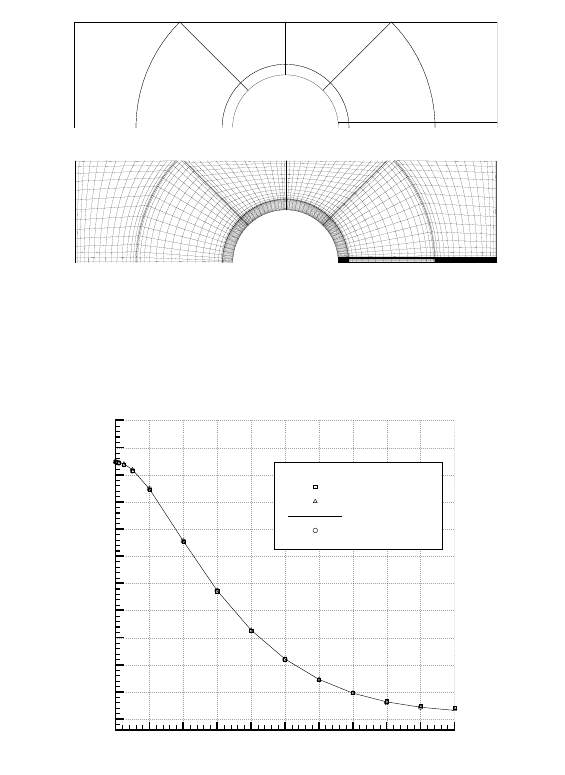
to N = 16 for all variables. The topology of the grid and the Gauss-Lobatto grid

near the cylinder are shown in Fig. 27. Note the small spectral elements around

the cylinder and in the wake of the cylinder. Especially near the rear stagnation

point a very small spectral element is placed to capture the high stress-gradients. In

order to compare the results obtained with D-LSQSEM-DM the non-dimensional

drag coefﬁcient on the cylinder is compared with results reported in [2]. The drag

coefﬁcient is deﬁned as

surf. cyl

(

− pI) ·n

dS , (124)

where n

is the x-component of the outward unit normal at the cylinder and U is

the bulk velocity. The inﬂuence of elasticity in the ﬂow is denoted by the Deborah

number, De

De =

. (125)

Fig. 28 graphically displays the drag coefﬁcients as a function of De. From the

results presented above it can be concluded that D-LSQSEM-DM is capable of pro-

ducing drag coefﬁcients in agreement with those reported in [2]. However, agree-

220

Least-Squares Spectral Element Methods in Computational Fluid Dynamics

Fig. 27 Topology of the spectral elements in the vicinity of the cylinder (top ﬁgure) and the Gauss-

Lobatto grid for a polynomial degree N = 16

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

100

105

110

115

120

125

130

135

140

M60 SMART

M120 SMART

ext SMART

D-LSQSEM16

Fig. 28 Non-dimensional drag obtained with D-LSQSEM-DM with a polynomial degree N = 16

compared to the ﬁnite volume results using SMART discretization reported in [2]

ment of integral quantities does not necessarily imply pointwise agreement. There-

fore the contour plot of the extra-stress component in the xx-direction is compared

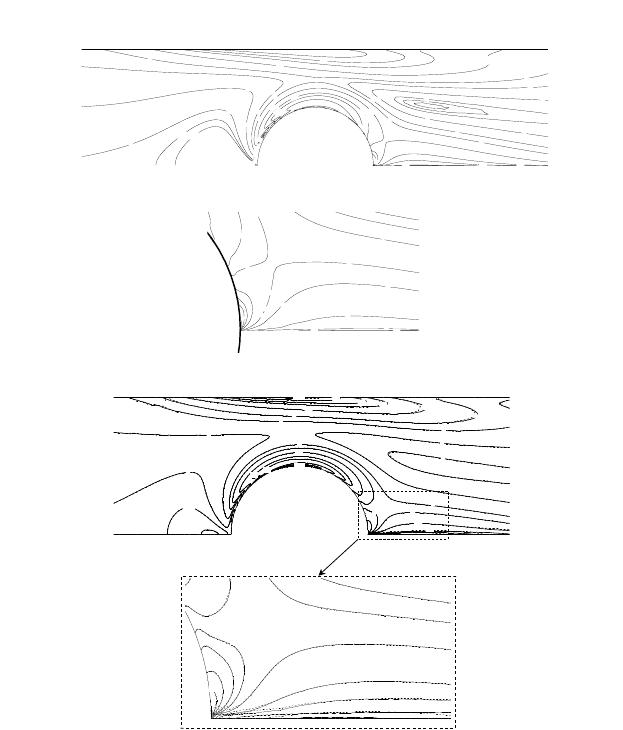
with Fig. 16 taken from [2] in Fig. 29.

This comparison demonstrates that no stabilization terms are required in the least

squares method to produce smooth and converged solutions; i.e. no oscillations are

present. Both contour plots display a similar pattern. The highest value of the

component obtained in the D-LSQSEM-DM calculation equals 128.96 at the cylin-

der. This value is in agreement with the stress levels reported in [2] and later con-

221

Marc Gerritsma and Bart De Maerschalck

-0.3

-0

-0.3

0.5

-0.3

100

120

0.5

Fig. 29 Contour lines of the

-component of the extra-stress tensor at De = 0.9 and detail of the

contours just behind the cylinder (top Figures) and comparison of contours of the normal stresses

(

) near the cylinder predicted with M60 (dashed line) and M120 (solid line), at De = 0.9. Taken

from [2] (lower Figure)

ﬁrmed in [1]. For further particulars on the use of LSQSEM for viscoelastic ﬂow

problems see [34].

222