Koren B., Vuik K. (Editors) Advanced Computational Methods in Science and Engineering
Подождите немного. Документ загружается.


Least-Squares Spectral Element Methods in Computational Fluid Dynamics
that the full potential of solving differential equations by minimizing well-posed
variational statements was recognized in mechanical engineering.
2.2 Galerkin formulations
It is not always possible to convert a differential equation to an associated mini-
mization problem. A well-known example with applications in fluid dynamics is
the steady linear advection equation given by
a
du
dx
= 0 , x ∈(0,1) , a > 0 , (21)
with boundary condition u(0) = u
0
. The method described by (16) is still applicable.
This gives
a(u,v) =
Z
Ω
a
du
dx
vd
Ω
= 0 . (22)
This formulation where the partial differential equation is weighted by a suitably
chosen set of test functions is called the Galerkin formulation. This weak formu-
lation does not correspond to a minimization problem and generally the space of
trial solutions, u, and test functions, v, are not the same. For the integral (22) to
make sense we need to have that u ∈ H
1
(0,1) and v ∈ L
2
(0,1), so a setting in terms
of Hilbert spaces is not possible. Consider the slightly more general case given by
Seek u ∈W such that: a(u,v) = f (v) , ∀v ∈V , (23)
where W and V are function spaces equipped with the norms k·k
W
and k·k
V
,
respectively. W is called the solution space and V is called the test space. We assume
that the bi-linear form is continuous as defined in Definition 1 and f ∈V
′
. Then the
following theorem establishes the conditions for well-posedness, [31]
Theorem 1. Let W be a Banach space and let V be a reflexive Banach space. Let
a ∈ L (W ×V;R) and f ∈V
′
, then problem (23) is well-posed if and only if
∃
α
, inf
w∈W
sup
v∈V
a(w, v)
kwk
W
kvk
V
≥
α
, (24)
∀v ∈V , (∀w ∈W , a(w,v) = 0) =⇒ (v = 0) . (25)
⊓⊔
This condition is referred to as the inf-sup condition, the Ladyzhenskaya-Babuˇska-
Brezzi (LBB) condition or the Banach-Neˇcas-Babuˇska condition. It is generally
quite hard for a given weak formulation to prove the existence of the positive con-
stant
α
, the coercivity constant.
In contrast to the minimization problem, well-posedness on the continuous level
does not imply well-posedness for discrete conforming subspaces W
h
⊂W and V
h
⊂
183
Marc Gerritsma and Bart De Maerschalck
V. This means that for every problem discrete function spaces need to be identified
such that well-posedness also holds for (W
h
,V
h
). Different weak formulations then
require different approximating subspaces. Such may be the case with multi-physics
simulations such as fluid-structure interaction problems.
In order to establish well-posedness and to develop a consistent and convergent
scheme a variety of stabilization operators are generally required.
2.3 Least-squares formulation
An alternative approach of establishing equivalence between differential equations
and weak formulations is offered by the so-called least-squares formulation. The
least-squares formulation transforms partial differential equations into a minimiza-
tion problem and in this sense extends the Rayleigh-Ritz formulation. The Rayleigh-
Ritz formulation is limited to elliptic, self-adjoint problems. The previous subsec-
tion, 2.1 and 2.2, demonstrated that it is favorable to have a weak formulation which
corresponds to a minimization problem, but that it is not always possible to convert
a partial differential equation in terms of a minimization problem. The least-squares
formulation provides a framework in which partial differential equations can be cast
into a minimization setting, thus retrieving the appealing properties of the Rayleigh-
Ritz principle.
This is established by introducing a norm equivalence between the residual and
the error. Two norms, k·k
X
and k·k
Y
, are called equivalent when two positive con-
stants, C
1
and C
2
, exist such that
C
1
kuk
X
≤ kuk
Y
≤C
2
kuk
X
, ∀u ∈X . (26)
If we define the linear spaces to be
X = {u|kuk
X
≤ ∞} and Y = {u|kuk
Y
≤ ∞} , (27)
norm-equivalence states that both sets contain the same elements, X = Y. Equivalent
norms on a function space X define the same topology and more specifically, Cauchy
sequences in both norms are the same. For finite-dimensional spaces all norms are
equivalent.
Let the abstract first order partial differential equation be given by
L u(x) = f(x) , ∀x ∈
Ω
, (28)
with
Ru(x) = g(x) , ∀x ∈
∂Ω
, (29)
where L is a first order linear partial differential operator and R is a linear trace
operator which prescribes boundary values. In the least-squares formulation, we
now look for function spaces, X and Y , with associated norms such that we have the
184

Least-Squares Spectral Element Methods in Computational Fluid Dynamics
norm-equivalence
α
kuk
X(
Ω
)
≤ kL uk
Y(
Ω
)
+ kRuk
Z(
∂Ω
)
≤Ckuk
X(
Ω
)
, ∀u ∈X . (30)
The space X is called the solution space and Y is called the residual space. Due to
the linearity of the differential and trace operator we have that, if u
ex
∈X
α
ku −u
ex
k
X(
Ω
)
≤ kL u − f k
Y(
Ω
)
+ kRu −gk
Z(
∂Ω
)
≤Cku −u
ex
k
X(
Ω
)
, ∀u ∈X ,
(31)
in which u
ex
denotes the exact solution of (28-29). This equivalence tells us that
small residual norms correspond to small error norms and conversely, small error
norms correspond to small residual norms.
Based on this equivalence we can now define the so-called least-squares func-
tional
J (u) =
1
2
n
kL u − f k
2
Y(
Ω
)
+ kRu −gk
2
Z(
∂Ω
)
o
. (32)
Solving the abstract PDE (28-29) is now equivalent to minimizing the least-squares
functional J (u). So by applying the least-squares formulation, the problem has
been recast in terms of a minimization problem thus avoiding stability prerequisites
such as inf-sup conditions as discussed in the previous section.
Minimization of the least-squares functional requires setting DJ (u)v = 0 for all
v ∈ X analogous to the minimization procedure described in Section 2.1. Note also
that the boundary conditions, Ru = g, are also incorporated in the minimization
process.
Without loss of generality, we can set g = 0 in the equation Ru = g. This al-
lows us to incorporate the boundary conditions in the space X. When we do so, the
boundary conditions are strongly enforced and can be dropped from the variational
statement.
If Y is a Hilbert space this gives the weak formulation
(L u,L v)
Y(
Ω
)
= ( f ,L v)
Y(
Ω
)
, ∀v ∈ X . (33)
Note that this formulation is symmetric; interchanging u and v on the left hand side
of this equation leaves the expression unchanged. Furthermore, the basic existence
and uniqueness criterion, the norm-equivalence, (30), is inherited by conforming
subspaces.
Although in the previous discussion general function spaces X and Y were
treated, from a practical point of view it is convenient to choose function spaces
which allow for easy calculation of the residual norm in the minimization process.
So in many applications, the boundary conditions are already incorporated in the
function space X and one takes Y (
Ω
) = L
2
(
Ω
). This leads to the least-squares func-
tional
J (u) =
1
2
kL u − f k
2
L
2
(
Ω
)
. (34)
185

Marc Gerritsma and Bart De Maerschalck
Minimization is in the L
2
-sense, so point-wise convergence, in the L
∞
-sense, is
only attained if the exact solution is sufficiently regular. The next section discusses
the construction of conforming finite-dimensional subspaces of the solution space
X.
3 Spectral element methods
Instead of seeking the minimizer over the infinite-dimensional space X we restrict
our search to a conforming subspace X
h
⊂X by performing a domain decomposition
where the solution within each sub-domain is expanded with respect to a polynomial
basis. The domain
Ω
is sub-divided into K non-overlapping quadrilateral open sub-
domains
Ω
k
:
Ω
=
K
[
k=1
¯
Ω
k
,
Ω
k
∩
Ω
l
= /0 , k 6= l . (35)
Each sub-domain is mapped onto the unit cube (−1, 1)
d
, where d = dim(
Ω
). Within
this unit cube the unknown function is approximated by polynomials. Generally a
spectral element method based on Legendre polynomials, L
k
(x) over the interval
[−1,1], is employed, [15, 22, 52]. We define the Gauss-Lobatto-Legendre (GLL)
nodes by the zeroes of the polynomial
1 −x
2
L
′
N
(x) , (36)
and the Lagrange polynomials, h
i
(x), through these GLL-points, x
i
, by
h
i
(x) =
1
N(N + 1)
(x
2
−1)L
′
N
(x)
L
N
(x
i
)(x −x
i
)
for i = 0, .. ., N , (37)
where L
′
N
(x) denotes the derivative of the Nth Legendre polynomial. For multi-
dimensional problems tensor products of the one-dimensional basis functions are
employed in the expansion of the approximate solution. We can therefore expand
the approximate solution in each sub-domain in terms of a truncated series of these
Lagrangian basis functions, which for d = 2 yields
u
N
(x,y) =
N
∑
i=0
N
∑
j=0
ˆu
i j
h
i
(x)h
j
(y), (38)
where the ˆu
i j
’s are to be determined by the least-squares method. If we have con-
verted a general higher order PDE to an equivalent first order system, C
0
-continuity
suffices to patch the solutions on the individual sub-domains together.
The integrals appearing in the least squares formulation, (34), are approximated
by Gauss-Lobatto quadrature
186

Least-Squares Spectral Element Methods in Computational Fluid Dynamics
Z
1
−1
f (x)dx ≈
P
∑
i=0
f (x
i
)w
i
, (39)
where w
i
are the GL weights given by
w
i
=
2
P(P + 1)
1
L
2
P
(x
i
)
, i = 0,. .. ,P ≥N . (40)
It has been shown in [19] that it is beneficial for non-linear equations possessing
large gradients to choose the integration order P higher than the approximation of
the solution, N.
The method is not restricted to higher order methods based on Legendre poly-
nomials. In [18] and [71] Lagrangian basis functions based on the Chebyshev poly-
nomials were used for non-linear, time-dependent hyperbolic equations and the in-
compressible Navier-Stokes equations, respectively. Other systems of orthogonal
polynomials can be easily introduced into the least-squares spectral element frame-
work.
From a practical point of view, only least-squares formulations which allow for
the use of C
0
-finite or spectral elements are usable. Since C
0
-finite or spectral el-
ement methods are based on piecewise continuously differentiable polynomials,
standard finite and spectral elements can be used, which results in a very practi-
cal method from an implementational point of view. This can be accomplished by
first transforming the system into a first order system and subsequently requiring
that only (scaled) L
2
-norms are used in the quadratic least-squares functional, see
(34). The transformation into a first order system has two important consequences.
First of all, the continuity requirements between neighboring spectral elements are
mitigated such that C
0
-finite or spectral elements can be used (in case the residuals
are measured by L
2
-norms). Secondly, the transformation will keep the condition
number of the resulting discrete system under control [3, 14, 16].
4 Convergence and a priori error estimates
The H
1
− and L
2
-spaces are particularly suitable as the function spaces X and Y in
least-squares finite or spectral element methods resulting from the minimization of
first order partial differential equations with strongly imposed boundary conditions.
To appreciate this, assume that we have the following norm-equivalence
α
kuk
H
1
(
Ω
≤kL uk
L
2
(
Ω
)
≤Ckuk
H
1
(
Ω
)
, ∀u ∈X =
u ∈ H
1
(
Ω
) | Ru = 0 on
∂Ω
,
(41)
where the space X represents the space of functions which already satisfy the homo-
geneous boundary condition and for which the function itself and its first derivatives
are square integrable over the domain
Ω
. Based on the norm-equivalence (41), the
quadratic least-squares functional can be obtained which upon minimization yields
the weak formulation of the least-squares problem. If one uses a conforming finite-
187
Marc Gerritsma and Bart De Maerschalck
dimensional subspace X
h
⊂ X = H
1
(
Ω
), then one can approximate u
h
∈ X
h
by
piecewise continuously differentiable polynomials. In [68], it has been shown that
least-squares methods based on the norm-equivalence (41) yield the following error
estimate:
u −u
h
1
≤
˜
C inf
v
h
∈X
h
u −v
h
1
, (42)
where the constant
˜
C is given by
˜
C = 1 + 2C
2
/
α
2
, with the constants
α
and C from
(41). Here the subscript 1 in the norm k·k
1
refers to the Sobolev norm k·k
H
1
(
Ω
)
,
while k·k
0
will denote k·k
H
0
(
Ω
)
= k·k
L
2
(
Ω
)
.
Since the interpolation of the solution u in the space X
h
obviously belongs to the
finite-dimensional subspace X
h
, the right-hand side of equation (42) can be bounded
in the following way:
inf
v
h
∈X
h
u −v
h
1
≤
u −
π
h
N
(u)
1
, (43)
where
π
h
N
(u) ∈ X
h
represents the interpolation of the solution u ∈ X in the space X
h
consisting of polynomials of degree N. The right-hand side of expression (43) can
be further bounded from above if an h− or p−refinement strategy is used to obtain
a better approximation of the solution u ∈X. Since both refinement strategies result
in different estimates for the interpolation error (43) and hence in a different error
estimate (42), they are discussed separately hereafter.
u ∈ H
s
(
Ω
) for
some s ≥ 2
u −u
h
1
≤Ch
l
|u|
l+1
, (44)
where l = min(N,s−1) and where N represents the approximating order of the C
0
−
spectral elements and where h represents a grid parameter (for example, the maxi-
mum of the square root of the area of the spectral elements), which decreases with
increasing number of spectral elements. Here |·|
s
denotes the semi-norm defined by
|v|
2
s
=
∑
|
α
|=s
kD
α
vk
2
L
2
(
Ω
)
, (45)
where
α
is a multi-index given by the vector
α
= (
α
1
,.. .,
α
d
) , (46)
where the
α
i
are non-negative integers and
|
α
| =
α
1
+ ···+
α
d
(47)
We used the following notation for partial derivatives
188
Combining expression (43) with the interpolation error corresponding to h−
refinement, results in the following estimate if the exact solution

Least-Squares Spectral Element Methods in Computational Fluid Dynamics
D
α
=
∂
|
α
|
∂
x
α
1
1
∂
x
α
2
2
...
∂
x
α
d
d
. (48)
For example, if d = 2 and
α
= (1,2), then
D
α
u =
∂
3
u
∂
x
1
∂
x
2
2
. (49)
The rate of convergence (44) is optimal in the H
1
−norm since it provides the high-
est possible rate of convergence allowed by polynomials of degree N, [73]. Note
that the optimal rate of convergence depends on the polynomial degree (N) and the
regularity of the exact solution, denoted by the Sobolev exponent s. A similar rate of
convergence can be obtained for the L
2
−norm. In [73], it is shown that the following
L
2
−error estimate holds if the exact solution u ∈ H
s
(
Ω
) for some s ≥ 2:
u −u
h
0
≤Ch
l+1
|u|
l+1
. (50)
In case of p−refinement, the order N of the spectral elements is increased while
keeping the number of the spectral elements constant. Consequently, the grid pa-
rameter h remains constant. As a consequence, the convergence rates (44) and (50)
are not suitable in this case. In order to obtain useful convergence rates in case of
p−refinement, one can use the Legendre interpolation operator to bound the inter-
polation error u −
π
h
N
(u) from above. Assuming that u ∈ H
s
(
Ω
) for some s ≥ 2, it
can be proven [73, page 126] that
u −
π
h
N
(u)
k
≤CN
k−s
|u|
s
, with k = 0, 1, (51)
where
π
h
N
(u) represents the Legendre interpolation operator applied to the exact
solution u. Combining the latter expression with (42) and (43) results into the fol-
lowing error estimate
u −u
h
k
≤CN
k−s
|u|
s
, with k = 0, 1. (52)
Note that the rate of convergence is only bounded by the smoothness degree of the
solution s and not by any other grid parameter h as it occurs in the finite element
case. As a consequence, exponential convergence rates can only be obtained for
smooth problems if a p-refinement strategy is used. Since this rate of convergence
results from p-refinement, it is called p-convergence hereafter.
Least-squares formulations based on the norm-equivalence (41) are called fully
H
1
-coercive formulations and they have optimal h−convergence rates in the H
1
-
and L
2
-norms. Moreover, if the fully H
1
-coercive least-squares method is supple-
mented with strongly imposed boundary conditions, one can use standard finite and
spectral elements. Consequently, it is not so surprising that fully H
1
-coercive for-
mulations with strongly imposed boundary conditions are the preferred setting for
189

Marc Gerritsma and Bart De Maerschalck
least-squares finite and spectral element methods since these methods are both prac-
tical and optimally accurate.
Note that the above a priori estimates only depend on continuity and coercivity of
the differential operator L and interpolation estimates. In [69, 70] these error esti-
mates have been confirmed numerically with the use of Legendre polynomials. But
since the estimates are independent of the type of orthogonal basis functions used,
similar results will hold for polynomials such as Chebyshev polynomials. These er-
ror estimates will play a role in hp-adaptive schemes to be discussed in Section 7.1.
Unfortunately, not all differential equations can be converted into H
1
-coercive
least-squares formulations. Especially compressible, inviscid flows which exhibit
shocks or contact discontinuities and models like Burgers’ equation do not fit in the
H
1
-coercive framework and therefore require a different treatment to be discussed
in Section 6.
5 Incompressible flows
For incompressible flows we can distinguish three regimes, the case where the
Reynolds number is so low that the convective terms can be neglected (Stokes flow),
the case where the Reynolds number is sufficiently small to yield steady solutions
and for slightly higher Reynolds numbers, we have time-dependent flow.
Stokes flow has been thoroughly discussed by Proot, [69, 70]. All function spaces
for which norm-equivalence can be established have been identified in these papers.
In this chapter we will show some applications to steady and unsteady incompress-
ible, viscous flow problems.
5.1 Governing equations
In terms of the primitive variables (u, p) the governing equations read
∂
u
∂
t
+ (u ·∇)u = −∇p +
1
Re
∆
u+ f in
Ω
, (53)
∇·u = 0 in
Ω
, (54)
where u represents the velocity vector, p the kinematic pressure, f the forcing term
per unit mass (if applicable) and Re the Reynolds number.
190

Least-Squares Spectral Element Methods in Computational Fluid Dynamics
5.2 The first order formulation of the Navier-Stokes equations
In order to obtain an equivalent first order formulation of the unsteady Navier-Stokes
equations, the vorticity
ω
has been introduced as an auxiliary variable. By using the
identity ∇×∇×u = −
∆
u+ ∇(∇·u) and by using the incompressibility constraint
∇·u = 0, the governing equations subsequently read
∂
u
∂
t
+ u ·∇u + ∇p +
1
Re
∇×
ω
= f in
Ω
, (55)
ω
−∇ ×u = 0 in
Ω
, (56)
∇·u = 0 in
Ω
, (57)
where, in the particular case of the two-dimensional problem, u
T
= [u
1
,u
2
] repre-
sents the velocity vector, p the kinematic pressure, f
T
= [ f
1
, f
2
] the forcing term per
unit mass (if applicable) and Re is the Reynolds number.
5.3 Linearization of the non-linear terms
Before the least-squares principles can be applied and the corresponding weak form
discretized with spectral elements, the convective term u·∇u must be linearized. To
this end, one can use a Picard (e.g. successive substitution)
u·∇u ≈ u
0
·∇u, (58)
or a Newton linearization
u·∇u ≈ u
0
·∇u + u ·∇u
0
−u
0
·∇u
0
. (59)
In the latter two equations, the subscript “0” indicates that the value of the corre-
sponding variable is known from the previous iteration step.
If Picard linearization is used the following linearized momentum equation is
obtained:
∂
u
∂
t
+ (u
0
·∇u + ∇p +
ν
∇×
ω
−f) = 0 . (60)
For steady problems the time derivative can be dropped. For time-dependent calcu-
lations either a time-stepping scheme needs to be selected or space-time elements
can be used, [19, 20, 21, 26, 63].
The least-squares formulation now becomes: Find u, p,
ω
∈ H
1
(
Ω
) which mini-
mizes the functional in the absence of body forces
I (u, p,
ω
) = k∇·uk
2
L
2
+ k
ω
−∇ ×uk
2
L
2
+
191
Marc Gerritsma and Bart De Maerschalck
∂
u
∂
t
+ (u
0
·∇u + ∇p +
ν
∇×
ω
)
2
L
2
. (61)
Variational analysis with respect to the four unknowns u, p and
ω
leads to the sym-
metric positive definite system.
5.4 Steady flow around a cylinder at low Reynolds
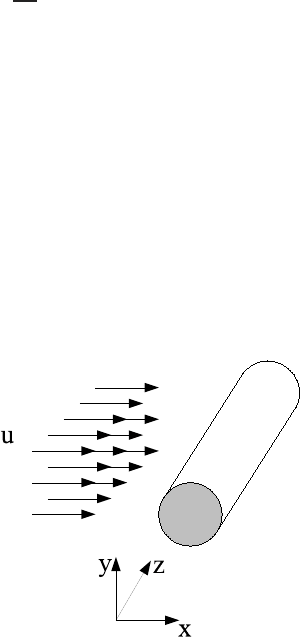
One of the test cases considered for LSQSEM is the steady flow around a circular
cylinder. This research was performed by De Groot, [41], with the conventional
least-squares method discussed above and Direct Minimization, see Section 7.2.
Here we are simulating the flow around a circular cylinder placed perpendicularly
in a uniform parallel flow, see Fig. 1.
Fig. 1 Description of the flow problem
It is known that for flows with Reynolds numbers Re < 45 a steady solution exists
and for Reynolds number higher than Re = 45 time-dependent behaviour sets in and
the well-known Von Karman vortex street develops. The investigation of the flow
will be in the Reynolds range: 1 < Re < 45. In this range two different flow types
are observed. For Re < 6 the flow is completely attached to the cylinder as can be
seen in Fig. 2 (a). For Re > 6 the flow starts to separate somewhere on the cylinder
forming two attached eddies behind the cylinder, Fig. 2 (b). For a benchmark be-
tween LSQSEM on the one hand and experimental data on the other, the estimation
of the Re number for which the twin vortices appear, is an important property of the
flow. This Re number is from here on referred to as Re
onset
. The twin vortices grow
in length and change shape as Re increases. The accurate prediction of this relation
is a common benchmark. Fig. 3 gives a schematic overview of the flow where two
steady vortices exist behind the cylinder.
192
